Исследование лингвистических модификаторов нечётких множеств в среде MathСad

1. Исследование лингвистических модификаторов нечётких множеств в среде MathСad

Подготовила ст. гр. 649:
Шестакова Л.Н.
Руководитель:
доц. каф. ВМ РГРТУ
Конюхов А.Н.
Рязань, 2018

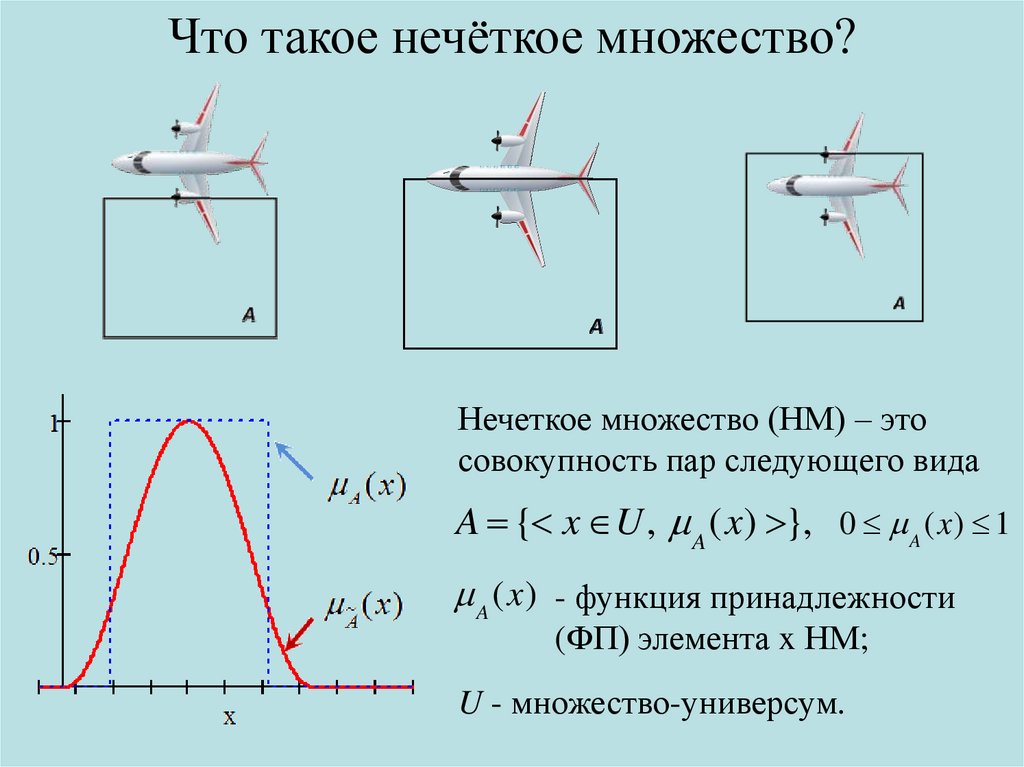
2. Что такое нечёткое множество?

Нечеткое множество (НМ) – это
совокупность пар следующего вида
A { x U , A ( x ) }, 0 A ( x ) 1
A ( x ) - функция принадлежности
(ФП) элемента x НМ;
U - множество-универсум.

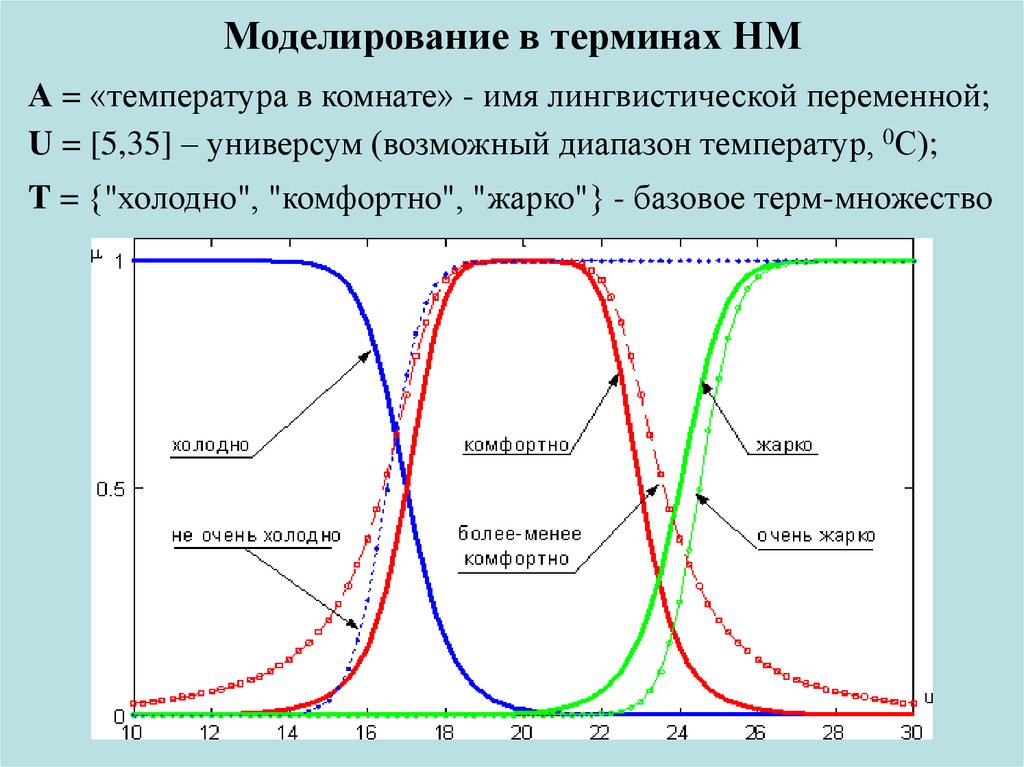
3. Моделирование в терминах НМ

А = «температура в комнате» - имя лингвистической переменной;
U = [5,35] – универсум (возможный диапазон температур, 0С);
T = {"холодно", "комфортно", "жарко"} - базовое терм-множество

4. Что такое лингвистические модификаторы?

Лингвистические модификаторы или «хеджи» (англ. hedges) определяются как слова, способные изменять
аспекты значений других слов, на которые они направлены.
Как правило, каждому лингвистическому модификатору
ставится в соответствие некоторый оператор, оказывающий
необходимое воздействие на исходное нечеткое множество.
1. Оператор концентрирования (с параметром k>1)
(смысловые оттенки - ОЧЕНЬ, СИЛЬНО)
CON
k
A
( x) CON k ( A ( x)) ( A ( x)) .
k

5.

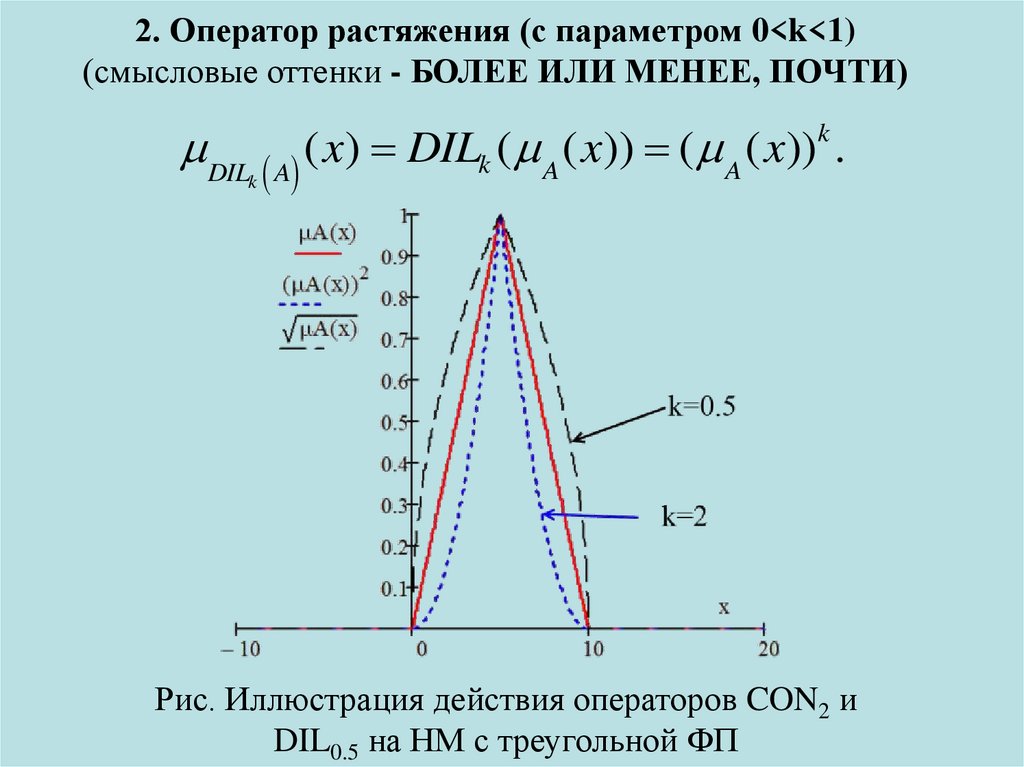
2. Оператор растяжения (с параметром 0<k<1)
(смысловые оттенки - БОЛЕЕ ИЛИ МЕНЕЕ, ПОЧТИ)
DIL
k
(
x
)
DIL
(
(
x
))
(
(
x
))
.
k
A
A
k A
Рис. Иллюстрация действия операторов CON2 и
DIL0.5 на НМ с треугольной ФП

6.

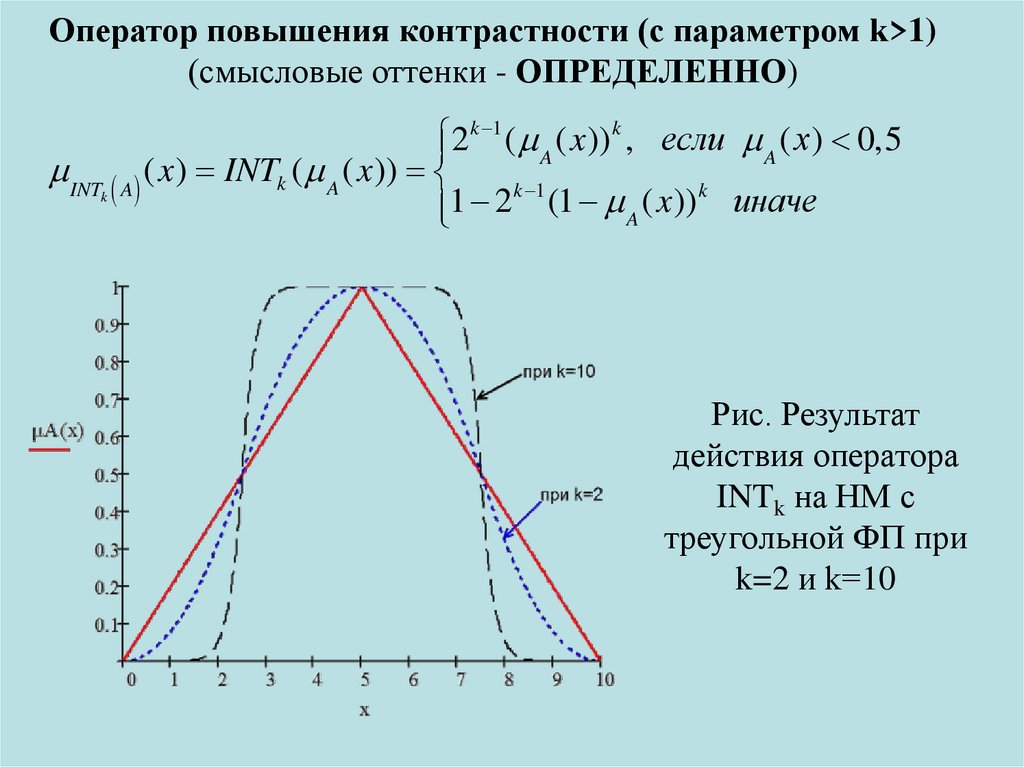
Оператор повышения контрастности (с параметром k>1)
(смысловые оттенки - ОПРЕДЕЛЕННО)
2k 1 ( A ( x )) k , если A ( x ) 0,5
INT A ( x ) INTk ( A ( x ))
k 1
k
k
1
2
(1
(
x
))
иначе
A
Рис. Результат
действия оператора
INTk на НМ с
треугольной ФП при
k=2 и k=10

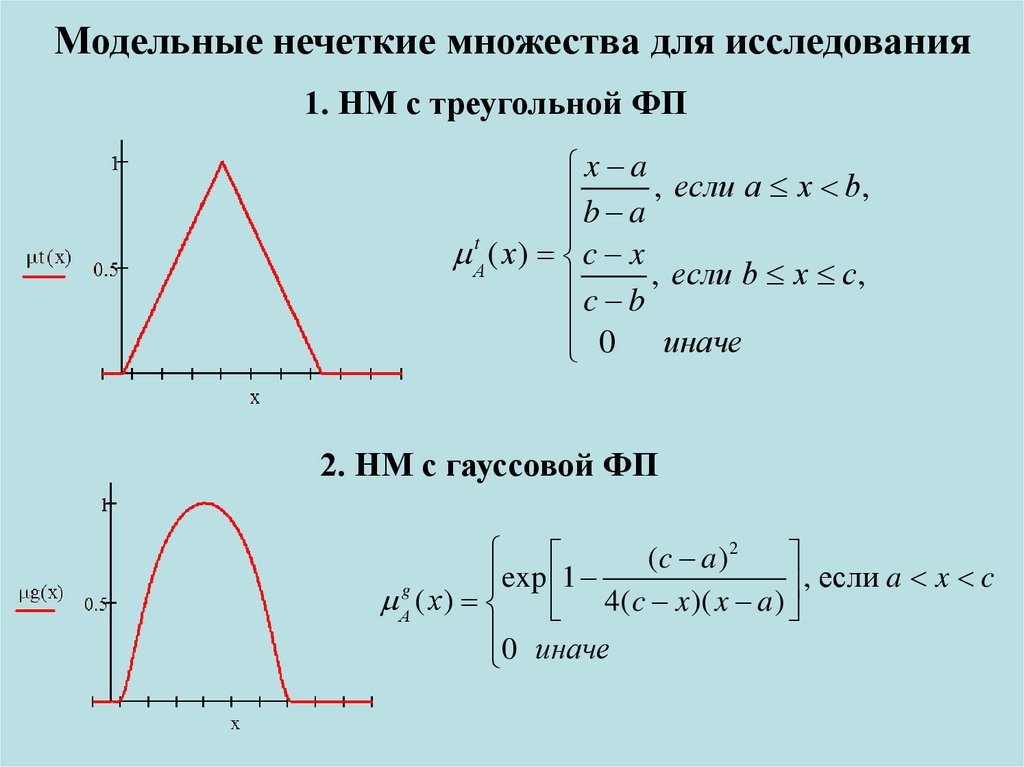
7. Модельные нечеткие множества для исследования

1. НМ с треугольной ФП
x a
b a , если a x b,
t
А ( х) c x
, если b x c,
c b
0 иначе
2. НМ с гауссовой ФП
(c a )2
, если a x c
exp 1
g
А ( х)
4( c x )( x a )
0 иначе

8.

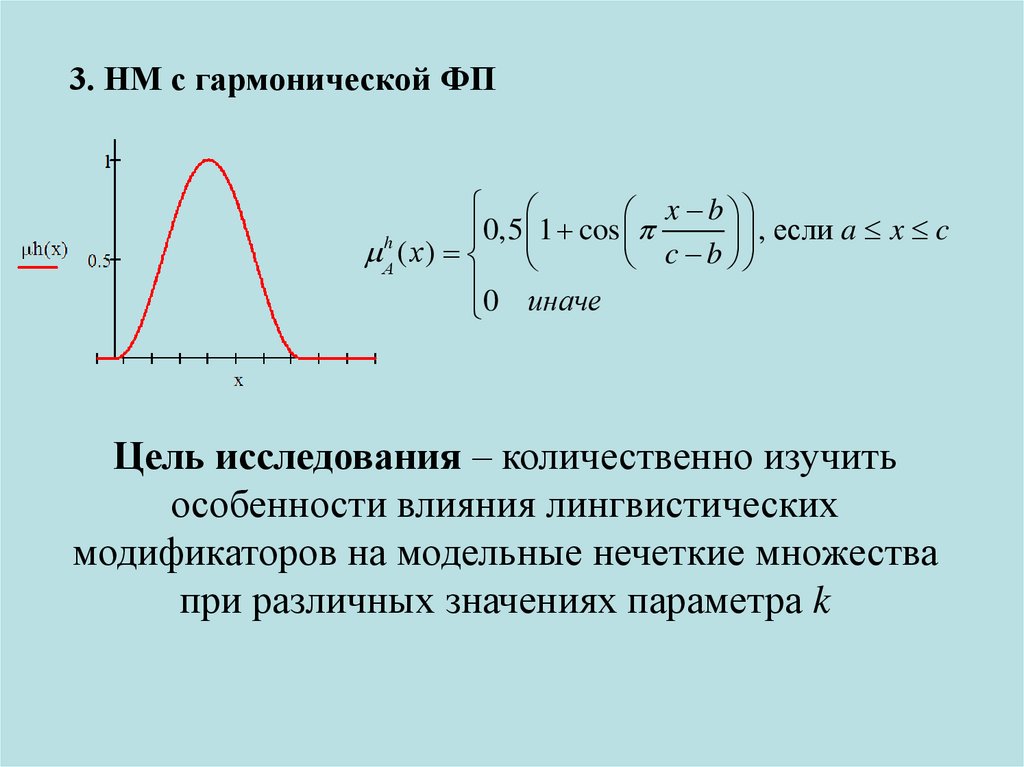
3. НМ с гармонической ФП
x b
, если a x c
0,5 1 cos
h
А ( х)
c b
0 иначе
Цель исследования – количественно изучить
особенности влияния лингвистических
модификаторов на модельные нечеткие множества
при различных значениях параметра k

9.

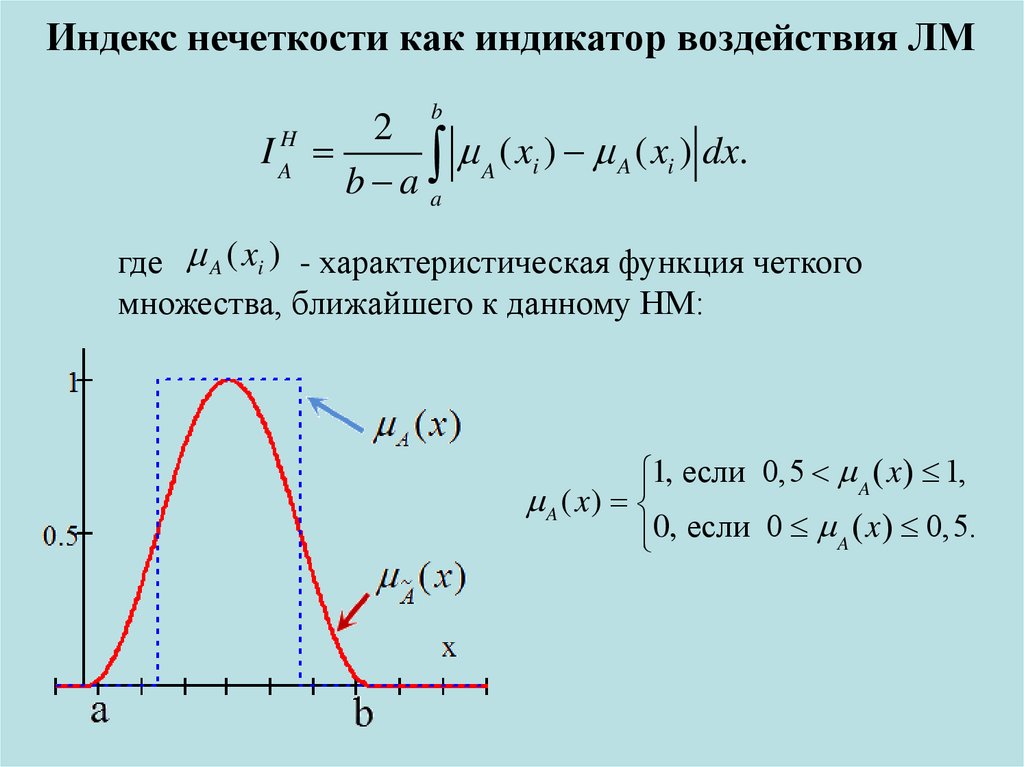
Индекс нечеткости как индикатор воздействия ЛМ
b
2
H
IA
A ( xi ) A ( xi ) dx.
b a a
где A ( xi ) - характеристическая функция четкого
множества, ближайшего к данному НМ:
1, если 0,5 A ( x ) 1,
A ( x)
0, если 0 A ( x ) 0,5.

10.

В качестве меры эффекта воздействия операторов
на НМ при каждом значении параметра k
рассчитывался коэффициент относительного
изменения индекса нечеткости
I0 Ik
(k )
,
I0
где I0 – индекс нечеткости исходного НМ
(предполагается I0 ≠ 0, т.е. исходное множество нечеткое); Ik – индекс нечеткости НМ, полученного
в результате воздействия оператора с параметром k.

11. Моделирование ЛМ в MathCad

12. Моделирование ЛМ в MathCad

13.

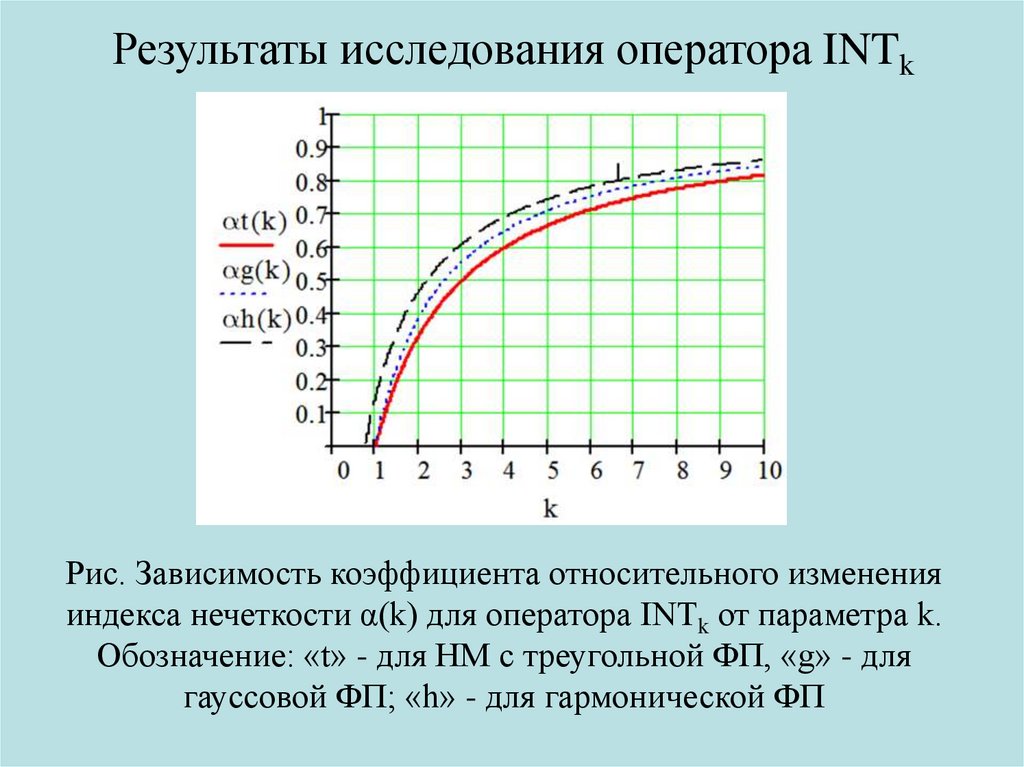
Результаты исследования оператора INTk
Рис. Зависимость коэффициента относительного изменения
индекса нечеткости α(k) для оператора INTk от параметра k.
Обозначение: «t» - для НМ с треугольной ФП, «g» - для
гауссовой ФП; «h» - для гармонической ФП

14.

Результаты исследования оператора DILk
Рис. Зависимость коэффициента относительного изменения
индекса нечеткости α(k) для оператора DILk от параметра k.

15.

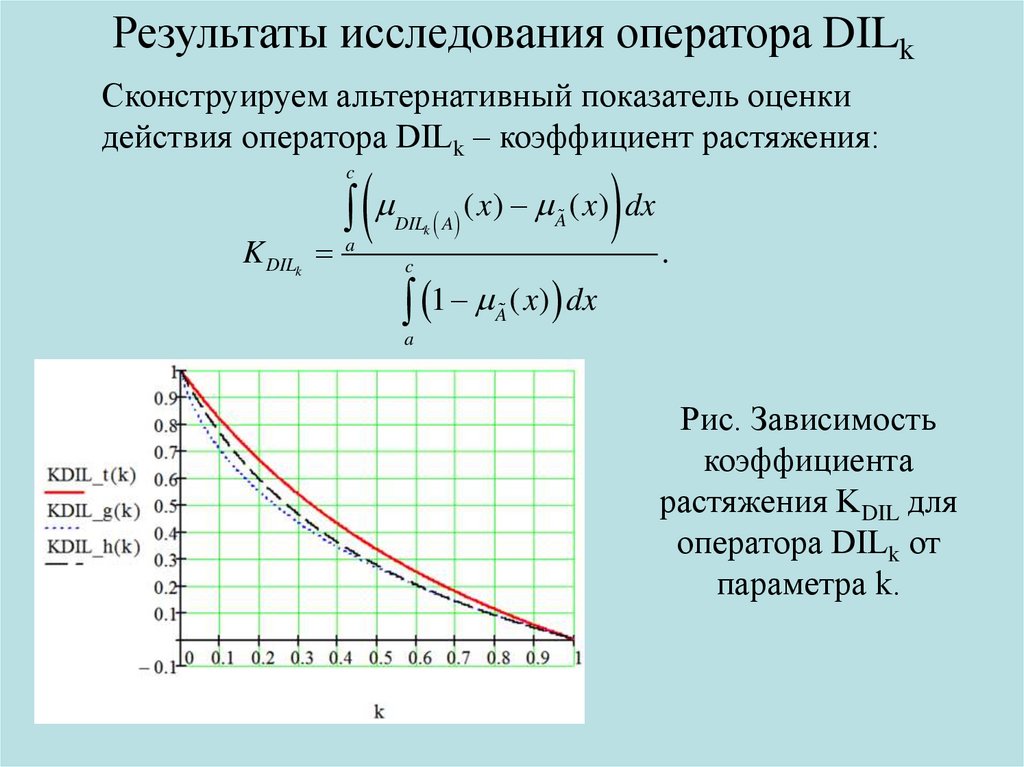
Результаты исследования оператора DILk
Сконструируем альтернативный показатель оценки
действия оператора DILk – коэффициент растяжения:
c
K DILk
DILk A
a
( x ) A ( x ) dx
c
1
A
( x ) dx
.
a
Рис. Зависимость
коэффициента
растяжения KDIL для
оператора DILk от
параметра k.

16.

Вывод
Применение пакета MathCad позволяет количественно
оценить эффект, оказываемый на нечеткие множества со
стороны параметризованных операторов (ЛМ), выявить
оптимальные условия их применения, а также возможные
ограничения.
Предлагаемый подход может быть применен для
совершенствования
математического
аппарата
лингвистических модификаторов.