Похожие презентации:
Регрессионный анализ
1.
Регрессионный анализ2. Определение
В основе регрессионного анализа лежитпредположение, что зависимая переменная
является функций одной или нескольких
независимых переменных. Тогда, зная
значения независимых переменных, мы
можем сделать прогноз об изменении
зависимой переменной.
Регрессионный анализ предполагает
построение регрессионного уравнения, его
оценку и анализ.
3. Уравнение парной линейной регрессии
Простейшей регрессионной модельюявляется парная линейная регрессия.
Уравнение парной линейной регрессии в
общем виде следующее:
у=b0+b1x , где
b0 – свободный член уравнения регрессии
(Константа);
b1 –коэффициент уравнения регрессии.
4. Требования к исходным данным регрессионного анализа
1.2.
Зависимая (результирующая) переменная должна быть
непрерывной количественной переменной. Независимая
переменная должна быть непрерывной или
дихотомической. Категориальные независимые
переменные с более чем двумя значениями
перекодируются в набор дихотомических переменных.
Изучаемая совокупность должна быть достаточно большой,
чтобы показатели связей были статистически надежными
(число единиц совокупности должно превосходить число
коррелируемых переменных не менее чем в 6-8 раз).
5. Требования к исходным данным регрессионного анализа
3.4.
5.
Каждое значение зависимой переменной должно быть независимо
от других значений. Такие зависимости возникают если опрашивать
одного и того же респондента в разные периоды времени или
опрашивать респондентов, объединенных в группы (семья, бригада
и т. д.).
Распределение зависимой переменной должно быть близким к
нормальному и не иметь явных выбросов.
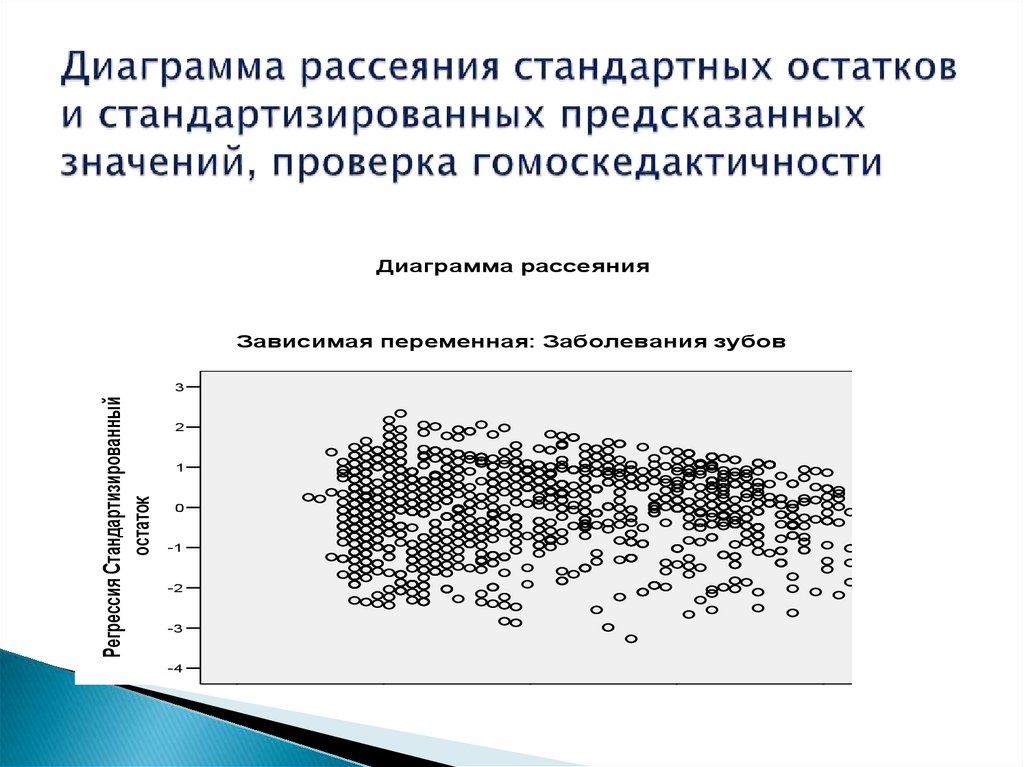
Должно выполняться требование гомоскедактичности, что означает,
что ошибки не становятся меньше, если уменьшается значение у и не
растут с увеличением значений у. Это предположение проверяется
при построении диаграммы рассеяния между стандартизованными
остатками и стандартизованными предсказанными значениями. Если
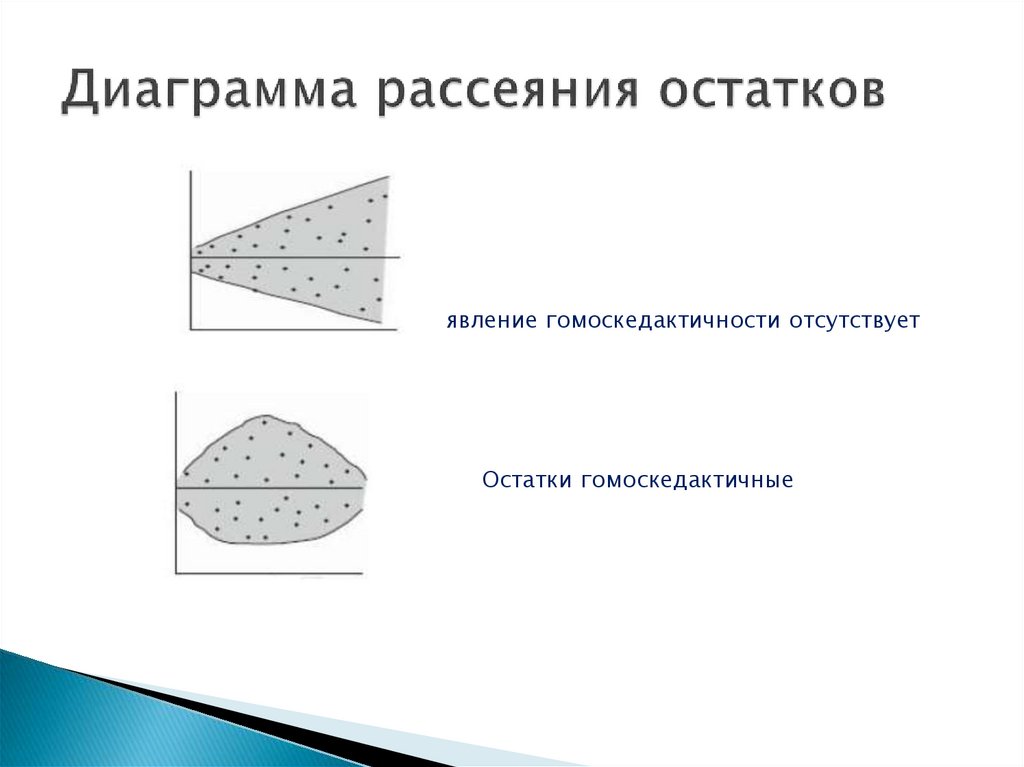
облако рассеяния овальное – данные гомоскедактичные. Если
облако рассеяния принимает форму конуса, требование
гомоскедактичности нарушается и данные являются
гетероскедактичными.
6. Требования к исходным данным регрессионного анализа
6.7.
Ошибка предсказания для каждого значения не должна
зависеть от ошибки предсказания других значений (тест
Дарбина-Уотсона), остатки должны быть нормально
распределены (график остатков).
Для случая множественной регрессии должно
отсутствовать явление мультиколлинеарности, которое
возникает, когда независимые переменные сильно
коррелируют между собой. Такого рода корреляция может
оказать сильное воздействие на зависимый признак и это
уже будет иное воздействие, чем независимых
переменных по отдельности.
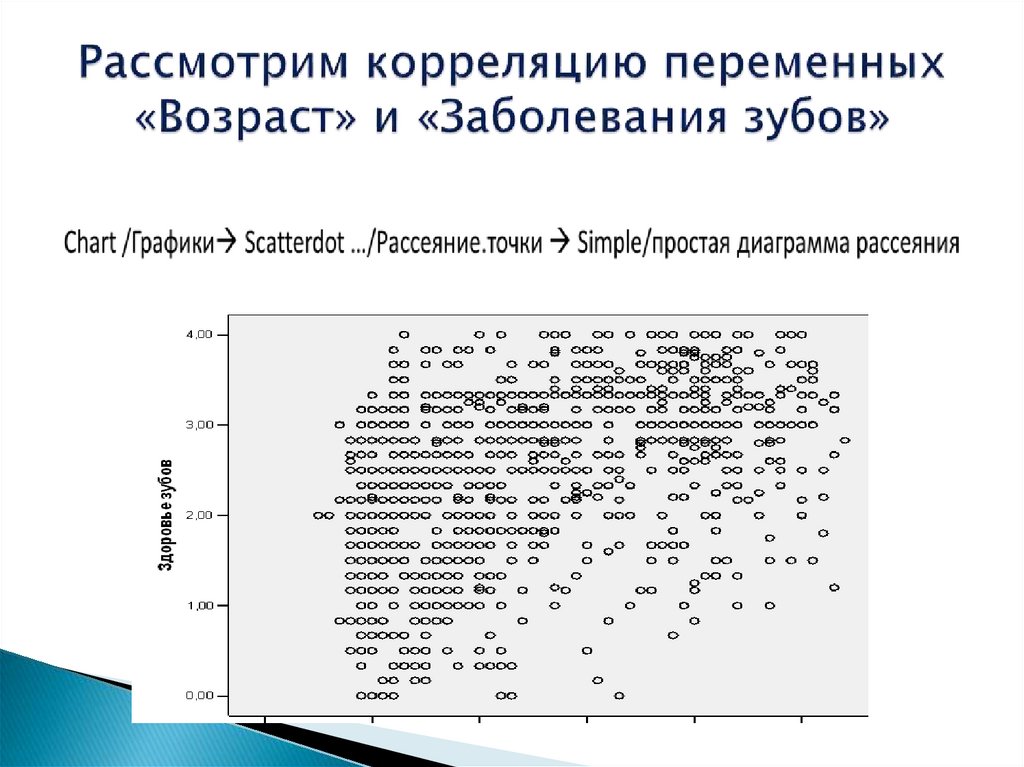
7. Пример:
Построить уравнение парной линейнойрегрессии для переменных «Возраст» и
«Заболевания зубов» (измеренной по
пятибалльной шкале, где 0 - здоровые
зубы, а 4 – наибольшая степень развития
заболевания)
8. Проверка причинно-следственной связи
1.2.
3.
Теоретически мы должны доказать, что
изучение связи между причиной и
следствием имеет смысл.
Причина всегда по времени должна
предшествовать следствию.
Причина должна коррелировать со
следствием.
9. Рассмотрим корреляцию переменных «Возраст» и «Заболевания зубов»
10. Проверка на наличие корреляции возраста и заболевания зубов
Analyze/ Анализ Correlation/КорреляцииBivariate/Парные
Correlations
Здоровье зубов
Возраст
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Здоровье
зубов
Возраст
1
,452**
.
,000
1130
1130
,452**
1
,000
.
1130
1130
**. Correlation is significant at the 0.01 level (2-tailed).
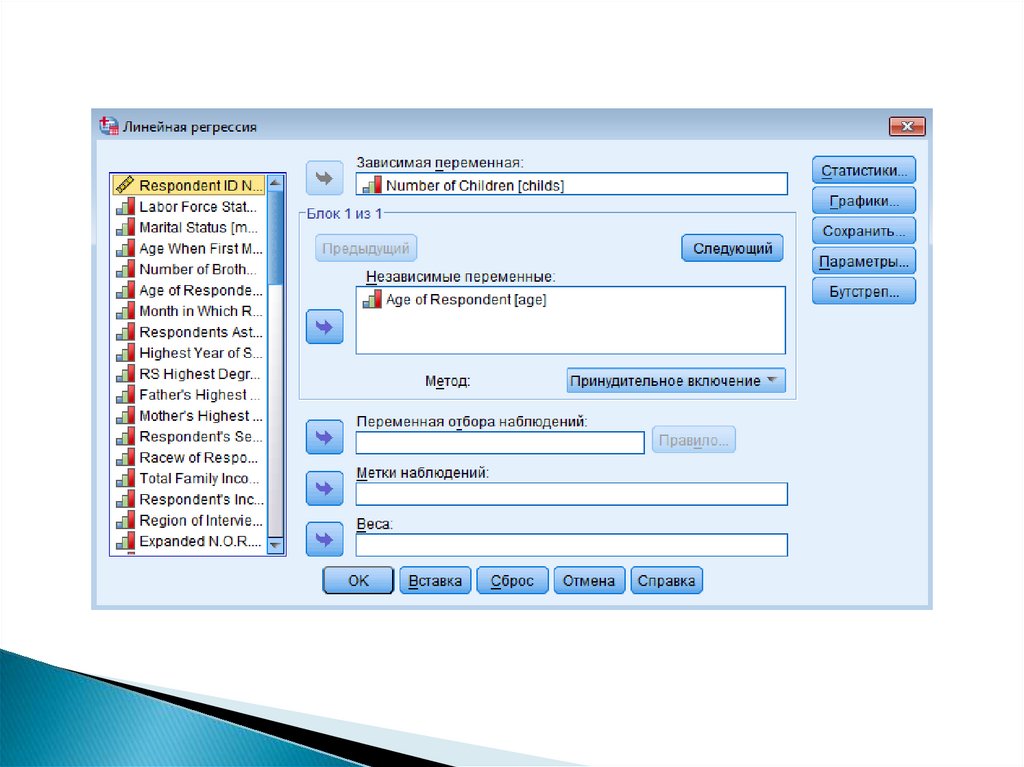
11. Построение парной линейной регрессии
Выполнение команды:Analyze/Анализ Regression/Регрессия
Linear/Линейная
В поле Dependent
Имя зависимой переменной
В поле Independent(s)
Имя независимой переменной
OK
12.
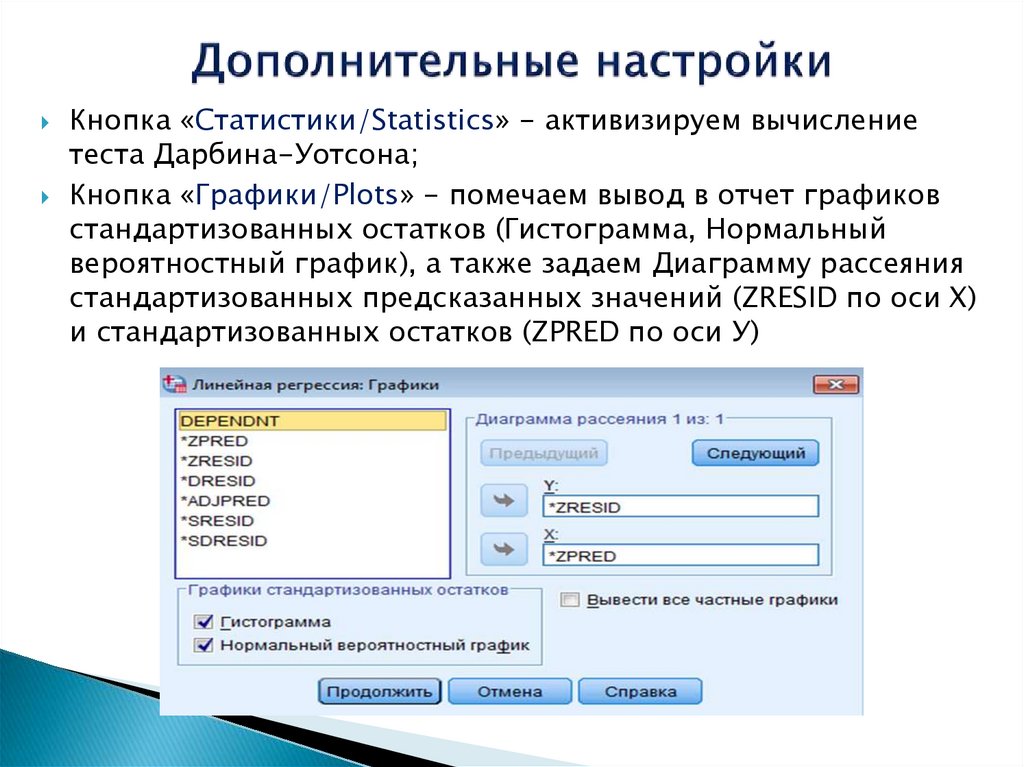
13. Дополнительные настройки
Кнопка «Статистики/Statistics» - активизируем вычислениетеста Дарбина-Уотсона;
Кнопка «Графики/Plots» - помечаем вывод в отчет графиков
стандартизованных остатков (Гистограмма, Нормальный
вероятностный график), а также задаем Диаграмму рассеяния
стандартизованных предсказанных значений (ZRESID по оси Х)
и стандартизованных остатков (ZPRED по оси У)
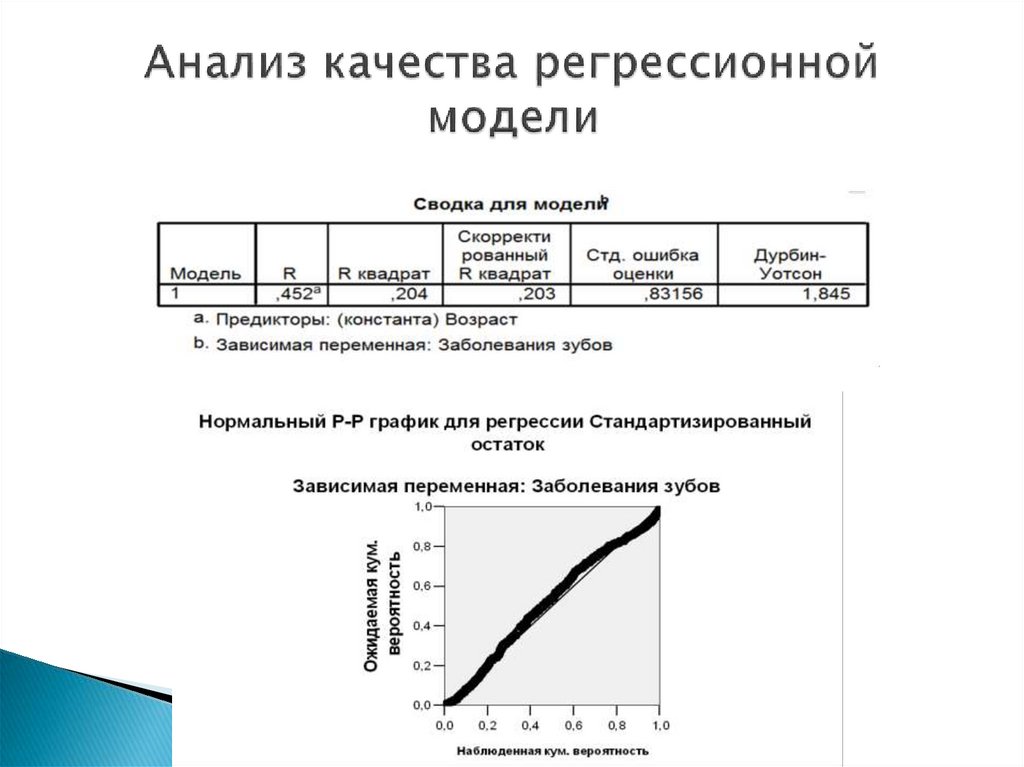
14. Результаты выполнения команд регрессионного анализа
у=1,295+0,033x15. Анализ качества регрессионной модели
16. Диаграмма рассеяния стандартных остатков и стандартизированных предсказанных значений, проверка гомоскедактичности
Диаграмма рассеянияЗависимая переменная: Заболевания зубов
Регрессия Стандартизированный
остаток
3
2
1
0
-1
-2
-3
-4
-2
-1
0
1
2
Регрессия Стандартизированное предсказанное значение
17. Диаграмма рассеяния остатков
явление гомоскедактичности отсутствуетОстатки гомоскедактичные
18. Множественная линейная регрессия
В большинстве задач следствие не можетбыть объяснено одной единственной
причиной; как правило, приходится изучать
влияние на него нескольких причин
одновременно. Для исследования такой
множественной связи используется
уравнение множественной линейной
регрессии:
19. Пример:
Построить уравнение множественнойлинейной регрессии для зависимой
переменной «Заболевания зубов» и
независимых переменных «Возраст»,
«Периодичность чистки зубов».
20. Множественная линейная регрессия
Выполнение команды:Analyze Regression Linear
В поле Dependent
Имя зависимой переменной
В поле Independent(s)
Имена независимых переменных
Дополнительные вычисления аналогичны
парной регрессии
21. Выбор метода анализа
В случае множественной регрессии можноиспользовать установленный по умолчанию
метод Enter (включения всех переменных в
модель одновременно)
или специальный пошаговый метод
Stepwise (модель строиться не для всех
исходных причин сразу, а пошагово в
модель включаются новые причины,
оговоренные в условии)
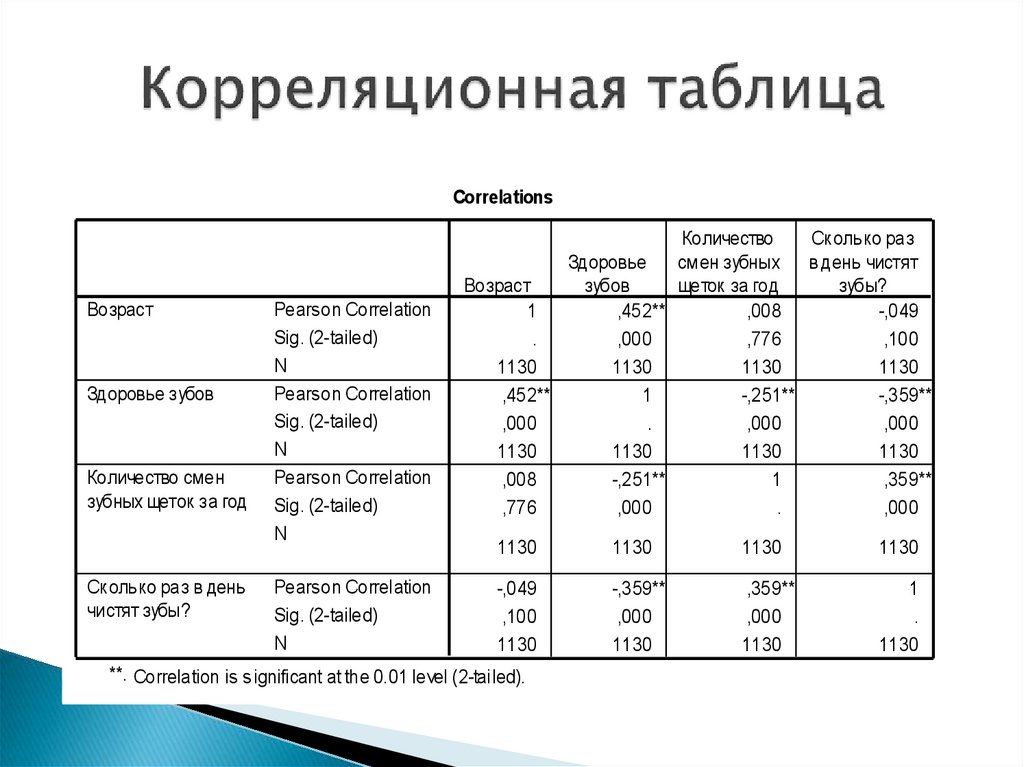
22. Корреляционная таблица
CorrelationsВозраст
Здоровье зубов
Количество смен
зубных щеток за год
Сколько раз в день
чистят зубы?
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Количество
Сколько раз
Здоровье
смен зубных в день чистят
Возраст
зубов
щеток за год
зубы?
1
,452**
,008
-,049
.
,000
,776
,100
1130
1130
1130
1130
,452**
1
-,251**
-,359**
,000
.
,000
,000
1130
1130
1130
1130
,008
-,251**
1
,359**
,776
,000
.
,000
1130
1130
1130
1130
-,049
,100
1130
-,359**
,000
1130
,359**
,000
1130
1
.
1130
**. Correlation is s ignificant at the 0.01 level (2-tailed).
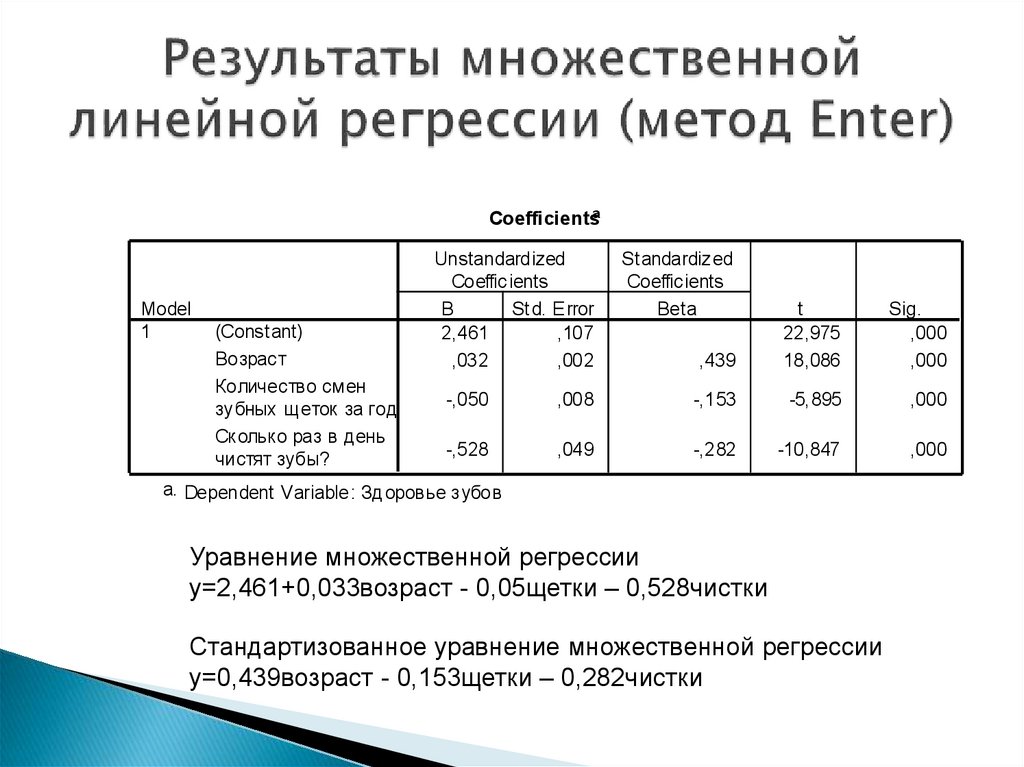
23. Результаты множественной линейной регрессии (метод Enter)
Coeffi cientsaModel
1
(Const ant)
Возрас т
Количество смен
зу бных щеток за год
Сколько раз в день
чистят зубы?
Unstandardized
Coeffic ients
B
St d. Error
2,461
,107
,032
,002
St andardiz ed
Coeffic ients
Beta
,439
t
22,975
18,086
Sig.
,000
,000
-,050
,008
-,153
-5, 895
,000
-,528
,049
-,282
-10,847
,000
a. Dependent Variable: Зд оровье зубов
Уравнение множественной регрессии
у=2,461+0,033возраст - 0,05щетки – 0,528чистки
Стандартизованное уравнение множественной регрессии
у=0,439возраст - 0,153щетки – 0,282чистки
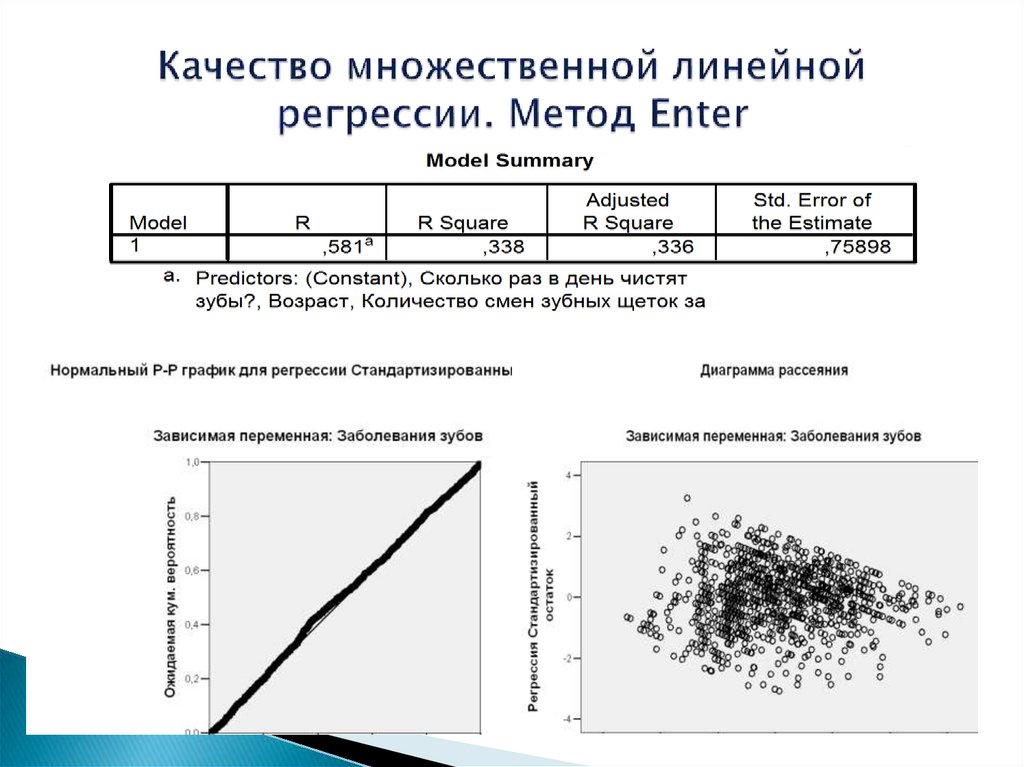
24. Качество множественной линейной регрессии. Метод Enter
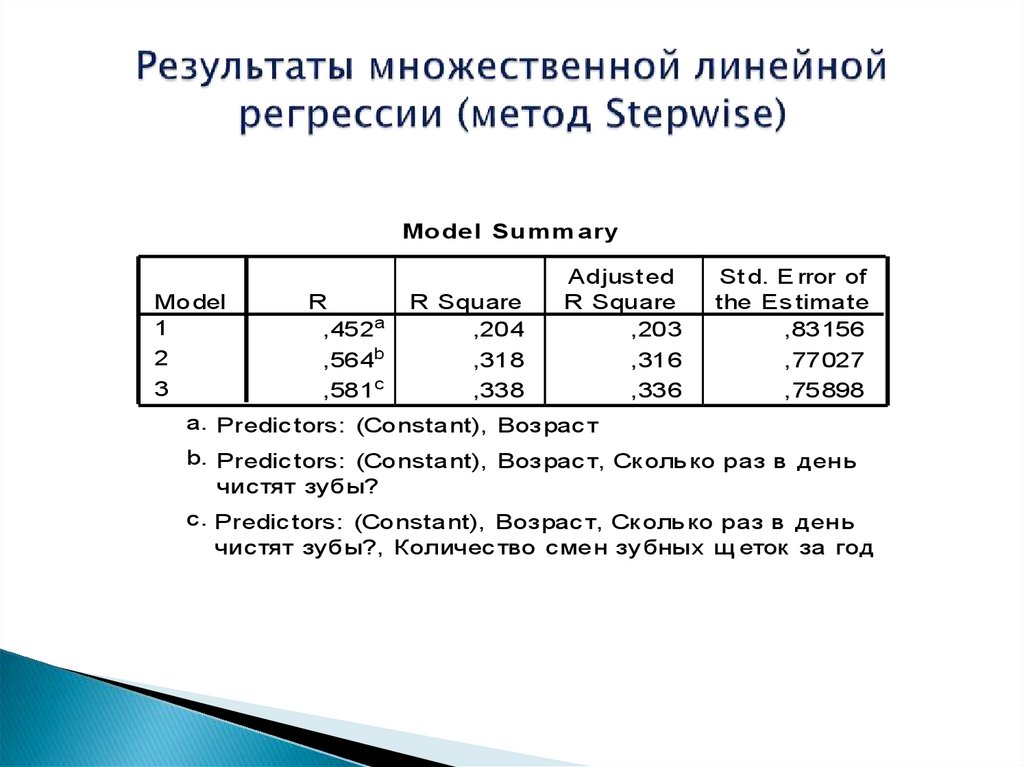
25. Результаты множественной линейной регрессии (метод Stepwise)
Model Summ aryModel
1
2
3
R
,452a
,564b
,581c
R Square
,204
,318
,338
Adjust ed
R Square
,203
,316
,336
St d. E rror of
the Es timate
,83156
,77027
,75898
a. Predic tors: (Constant), Возрас т
b. Predic tors: (Constant), Возрас т, Ск оль ко раз в день
чистят зубы?
c. Predic tors: (Constant), Возрас т, Ск оль ко раз в день
чистят зубы?, Количес тво смен зу бных щ еток за год
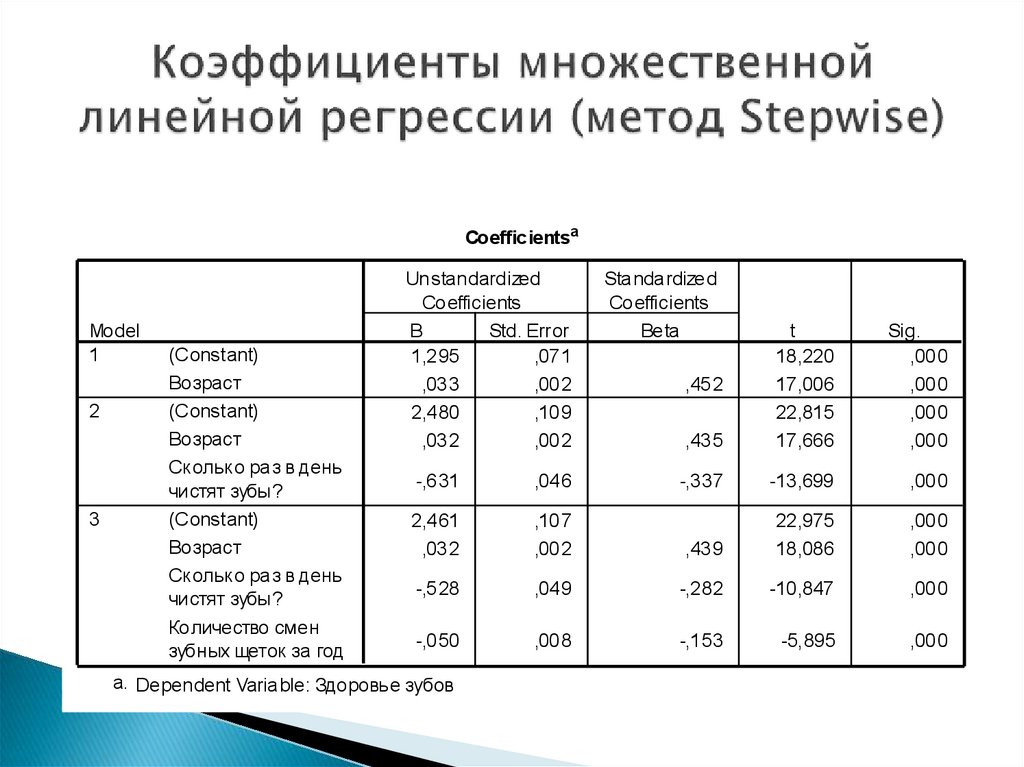
26. Коэффициенты множественной линейной регрессии (метод Stepwise)
CoefficientsaModel
1
2
3
(Constant)
Возраст
(Constant)
Возраст
Ск ольк о раз в день
чистят зубы?
(Constant)
Возраст
Ск ольк о раз в день
чистят зубы?
Количество смен
зубных щеток за год
Unstandardized
Coefficients
Std. Error
B
,071
1,295
,002
,033
,109
2,480
,002
,032
Standardized
Coefficients
Beta
,435
t
18,220
17,006
22,815
17,666
Sig.
,000
,000
,000
,000
-,337
-13,699
,000
,000
,000
,452
-,631
,046
2,461
,032
,107
,002
,439
22,975
18,086
-,528
,049
-,282
-10,847
,000
-,050
,008
-,153
-5,895
,000
a. Dependent Variable: Здоровье зубов















 Математика
Математика








