Похожие презентации:
Первообразная и интеграл
1.
Первообразнаяи интеграл
2.
Содержание•Первообразная
•Интеграл
а) неопределённый
б) определённый
3.
Первообразная4.
ОпределениеФункция F(х) называется
первообразной функции f(х) на
промежутке Х, если
x X
F ( x) f ( x)
На практике промежуток Х
обычно не указывают, но
подразумевают (область
определения функции).
Например: функция у = х²
является первообразной для
функции у=2х, т.к. для любого
х справедливо
(х²)´ = 2х.
5.
Теорема 1Если функция f(х)
непрерывна при
x X
,
то для
f(х) существует
первообразная F(х)
на Х.
6.
Теорема 2Если F(x) одна из
первообразных
функции f(x), на
промежутке Х, то у
функции у = f(x)
бесконечно много
первообразных, и все
они имеют вид у =
F(x)+C.
7.
Таблица первообразныхЗная
формулы для
нахождения
производных,
можно
составить
таблицу для
нахождения
первообразн
ых
f(x)
0
F(x)
C
1
x
x
x²/2
хn
х n 1
n 1
1/x
ln|x|
sinx
cosx
-cosx
sinx
х
ех
а
е
х
а х/lna
8.
Правила нахожденияпервообразных
Первообразная суммы
равна сумме
первообразных
2. Если F(x) – первообразная
для f(x), то к·F(x) – есть
первообразная для к· f(x).
3. Если F(x) – первообразная
для f(x), то первообразной
для функции у= f(кx+m)
служит функция у = 1/к·
F(кx+ m)
1.
9.
Найдём одну из первообразныхЕсли f(x) равно:
1) f(x)=2х+х³
2) f(x)=4х-2
3) f(x)=х³-3х²+х1
4) f(x)=4х⁵+2х+е
5) f(x)=х⁴+3х²+5
6) f(x)=5cosx3sin2x
Значит F(x) равно:
F(x)= х²+х⁴⁄4
F(x)=2х²-2х
F(x)=х⁴⁄42х³+х²⁄2-х
F(x)=2х⁶⁄3+х²+ех
F(x)=х⁵⁄5+х³+5х
F(x)=5sinx+3/2co
sx
10.
Ответить на вопрос:какая функция является
перообразной для
функции
f(x)= 2sinx – cosx?
А) cosx - 2sinx
Б) 2cosx - sinx
В) -2cosx - sinx
Г) –cosx + 2sinx
Ответ: в
11.
Выберите ответ, при которомпредложение будет верно.
Функция F(x) является
первообразной для функции f(x),
если:
А) F'(x) = f(x)
Б) F'(x) = - f(x)
В) f'(x) = F(x)
Г) f(x) = F(x)
Ответ: А
12.
Ответить на вопрос:для какой функции
первообразной является
функция
F(x)=2x³+6x²+x-9?
А) f(x) = 1/4·x⁴+2x³+x²-9x
Б) f(x) = 2x⁴+6x³+x²-9x
В) f(x) = 6x²+12x+1
Г) f(x) = x⁴⁄2+2x³+1/2·x²9x
Ответ: Г
13.
Ответить на вопрос:производная какой из
функций равна у = 4х - 3х²?
А) F(x) = 2x³-2x²+C
Б) F(x) = 2x²-1/3·x+C
В) F(x) = 2x²-x³+C
Г) F(x) = 4x²-x⁴+C
Ответ: В
14.
Задание №1. Найдитепервообразную функции f(x), график
которой проходит через точку А.
а) f(x)=5х+х², А(0;3)
б) f(x)=3х - 5,
А(4;10)
Решение. а) Найдём первообразные
F(x)= 5х²⁄2+х³⁄3+ С, где С –
произв.число.
Найдём это С:
т.к. график проходит через точку А(0;3),
то
F(0)= 5·0²⁄2+0³⁄3+ С = С и равно 3.
С=3
Значит производная, график которой
проходит через т. А, имеет вид:
F(x)= 5х²⁄2+х³⁄3+3.
15.
б)f(x)=3х - 5, А(4;10)
F(x)= 3х²⁄25х+С, где С – произв.
число.
F(4)= 3·4²⁄2-5·4+С=2420+С=4+С и
4+С=10 => С=6, тогда
F(x)= 3х²⁄2-5х+6
Ответ: F(x)=
3х²⁄2-5х+6
Решение.
16.
СамостоятельноНайдите первообразную
функции f(x), график
которой проходит через
точку А, если:
1) f(x)=х²-5, А(3;4)
2) f(x)=2х²+3, А(-2;-5)
3) f(x)=(х-2)², А(0;2)
4) f(x)=cos3x, А(0;1)
17.
Проверим ответы1) F(x)=
2) F(x)=
6(1/3)
3) F(x)=
4) F(x)=
х³⁄3 - 5х + 10
2х³⁄3 + 3х +
х³⁄3 - 2х² + 4х + 2
1/3·sin3x + 1
18.
Задание №2. Найдитепервообразную функции f(x),
значение которой при х = х₀ равно
у₀.
а) f(x)=10х⁴+х; х₀=0; у₀=6
Решение. F(x)= 10х⁵⁄5 + х²⁄2 + С
= 2х⁵+ х²⁄2 +С, где С – произв.
число.
Найдём С. Т.к. по условию
F(x₀)=у₀,
то F(0)=2·0⁵+0²⁄2+С=С и равно
у₀= 6.
Значит ответ: F(x)=2х⁵+х²⁄2+6
19.
б) f(x)=2sin3x+4cos(x/2);у₀=0
х₀=π⁄3;
Решение.
F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С=
=-2/3·cos3x+8· sin(x/2)+С, где С- пр.
ч.
Найдём С.
Т.к. по условию F(x₀)=у₀,
то F(π⁄3)=-2/3·cos
π+8sin(π/6)+С=
=2/3+8·1/2+С=4(2/3)+С и равно 0.
Тогда С = -4(2/3).
Значит F(x)=-2/3·cos3x+8· sin(x/2)4(2/3)
20.
в) f(x)=4+6х²; х₀=2; у₀<0Решение.
F(x)= 4х+6х³⁄3+С,
где С-п.ч.
Найдём С: т.к. F(х₀)= у₀ ,
то
F(2)= 4·2+6·2³⁄3+С=
8+16+С=24+С
и 24+С <0 => С <-24.
Пусть это будет (-25).
Тогда ответ F(x)= 4х+6х³⁄325
21.
г) f(x)=2х³+х²+3; х₀=1; у₀>0Решение.
F(x)= 2х⁴⁄4+х³⁄3+3х+С,
где С- пр.ч.
Найдём С.
F(1)= 2·1⁴⁄4+1³⁄3+3·1+С =
3(5/6)+С,
но 3(5/6)+С>0 => С > - 3(5/6)
Пусть С=-1, тогда
F(x)= 2х⁴⁄4+х³⁄3+3х-1
22.
Задание №3. Найдите множествопервообразных функции f(x).
а) f(x) =sin²x
sin5x·cos6x
б) f(x) =
Решение.
а) т.к. f(x) =sin²x
= (1 - cos2x)/2 = ½ - 1/2·cos2x,
то одна из первообразных равна:
F(x)=1/2·x - 1/4·sin2x.
Тогда множество всех
перообразных равно F(x)=1/2·x1/4·sin2x + С, где С –пр. число
23.
б) f(x) = sin5x·cos6xРешение. т.к. f(x) = sin5x·cos6x
=
=1/2·(sin11x-sinx),
то множество всех
первообразных данной
функции будет равно
F(x) =1/2·(-1/11·cos11x
+cosx)+C =
= 1/2· cosx – 1/22 ·cos11x
+С
24.
ИНТЕГРАЛЫ25.
ИНТЕГРАЛНеопределённый
интеграл
Определённый
интеграл
Обозначение:
b
f ( x ) dx
a
f ( x ) dx
26.
НЕОПРЕДЕЛЁННЫЙИНТЕГРАЛ
f ( x)dx
27.
Определение:Множество всех
первообразных функции f(x)
на некотором промежутке
называется неопределенным
интегралом от функции f(x)
на этом промежутке и
обозначается
f ( x)dx F ( x) C
28.
Основные свойстванеопределенного интеграла.
1.
f ( x)dx
f ( x ).
2. f x dx f ( x ) C.
3. kf ( x ) dx k f ( x ) dx.
т.е. постоянный множитель
можно выносить за знак
интеграла
29.
Основные свойстванеопределенного интеграла.
4. f1 x f 2 ( x) dx f1 ( x) dx f 2 ( x) dx.
1
5. f kx b dx F kx b C.
k
6. f x d g x f x g x g x d f x .
30.
Таблица основныхнеопределённых интегралов
kdx
k
x
C
n 1
х
n
х
dx
С
,
где
n
N
n 1
dx
1
x2 x C
dx
x
2 x C
31.
sinxdx
cos
x
C
cos
xdx
sin
x
C
dx
ctgx
C
sin 2 x
dx
tgx
C
cos 2 x
32.
Таблица интегралов33.
ОпределениеПроцесс нахождения
интеграла
называется интегрированием
Интегрирование является
операцией, обратной
дифференцированию
34.
ОПРЕДЕЛЁННЫЙИНТЕГРАЛ
b
a
f ( x)dx
35.
ОпределениеПусть функция y=f(x) определена и
интегрируема на отрезке [a,b] и пусть
F(x) – некоторая ее первообразная.
Тогда число F(b)–F(a) называется
интегралом от а до b функции f(x) и
обозначается
b
в
а
f ( x)dx F ( x)
a
36.
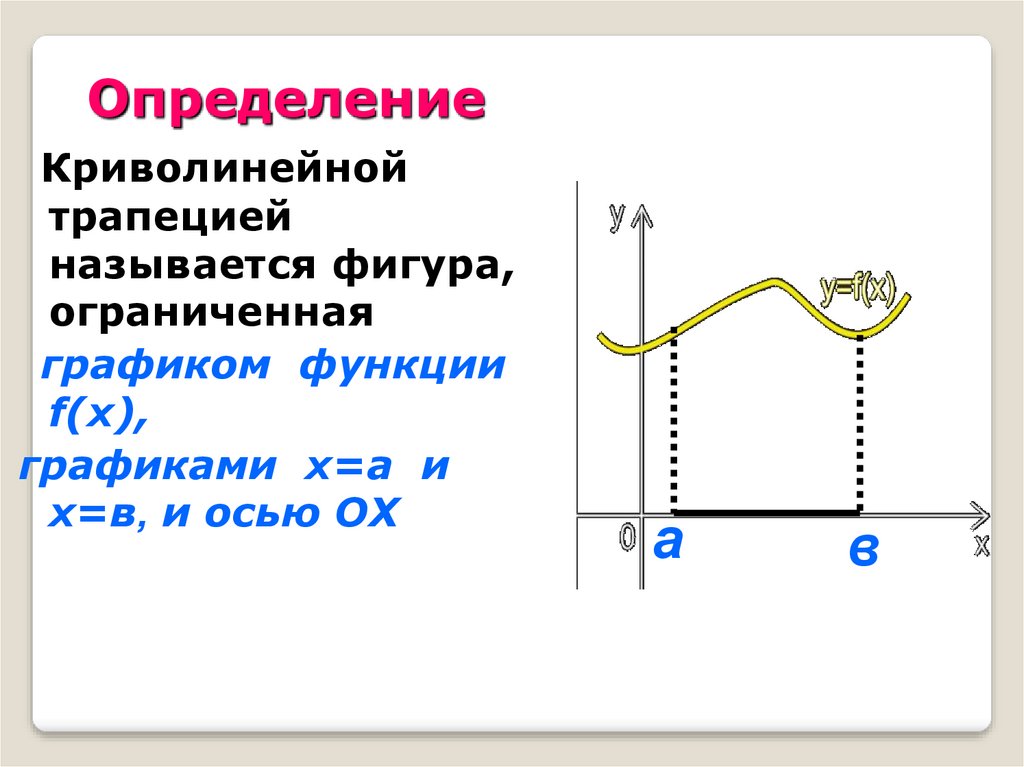
ОпределениеКриволинейной
трапецией
называется фигура,
ограниченная
графиком функции
f(x),
графиками х=а и
х=в, и осью ОХ
а
в
37.
Формула Ньютона-ЛейбницаТеорема: если функция у =
f(x) непрерывна на отрезке
[а;в], то справедлива
формула
b
a
f ( x)dx F (b) F (a)
Опираясь на эту формулу
получаются следующие свойства
определенного интеграла
38.
Свойства определенногоинтеграла
a
1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a
39.
Свойства определенногоинтеграла
b
b
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a
40.
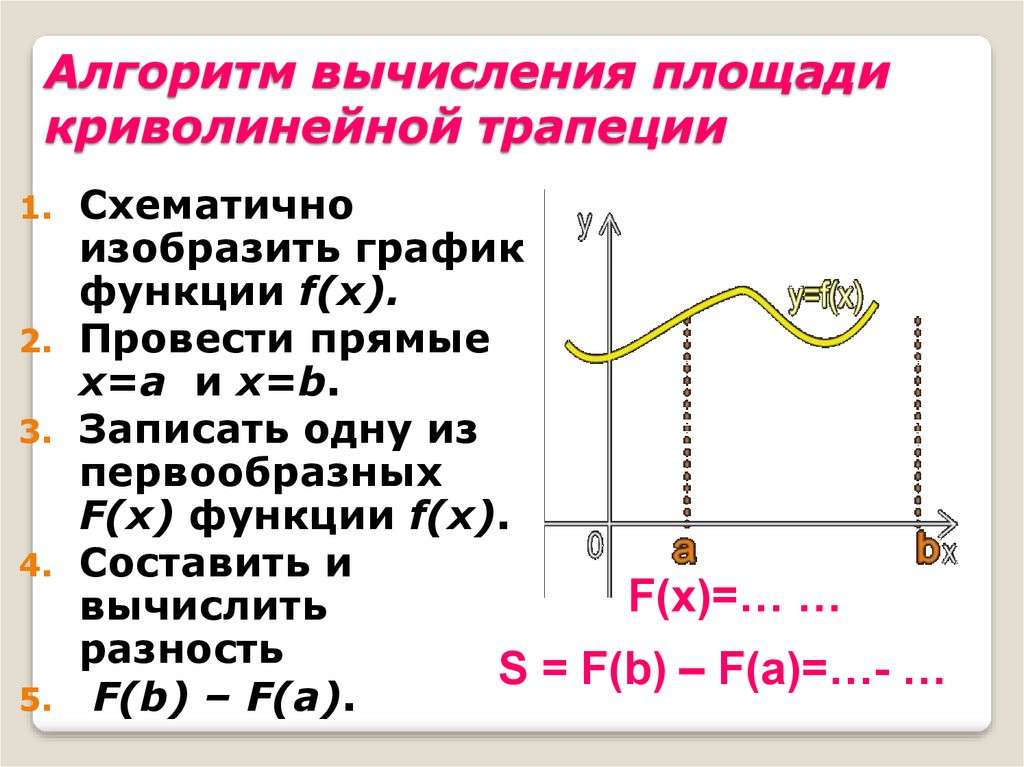
Алгоритм вычисления площадикриволинейной трапеции
1.
2.
3.
4.
5.
Схематично
изобразить график
функции f(x).
Провести прямые
x=a и x=b.
Записать одну из
первообразных
F(x) функции f(x).
Составить и
F(x)=… …
вычислить
разность
S = F(b) – F(a)=…- …
F(b) – F(a).
41.
Вычислить площадь фигуры,ограниченной линиями,
используя формулу НьютонаЛейбница
Вариант 1
f(x) = 2x – 3
y = 0,
x = 3,
x=5
Вариант 2
f(x) = – 2x – 3
y = 0,
x = – 5,
x= –3
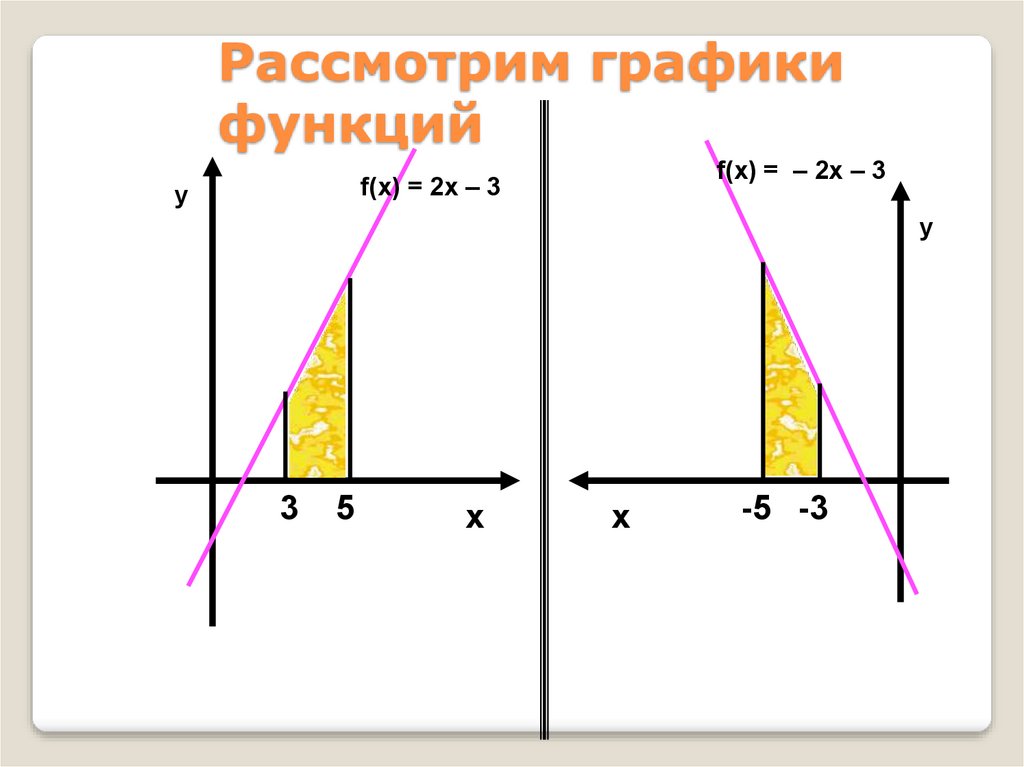
42.
Рассмотрим графикифункций
f(x) = – 2x – 3
f(x) = 2x – 3
у
у
3
5
х
х
-5 -3
43.
Проверим решениеВариант 1. Если f(x) = 2x – 3
F ( x) x 3 x
2
S F (5) F (3)
5 3 5 3 3 3
2
10 0 10
2
44.
Проверим решениеВариант 2. Если f(x) = – 2x – 3
F ( x) x 3 x
2
S F ( 3) F ( 5)
( 3) 3 ( 3)
2
( 5) 3 ( 5)
2
0 10 10
45.
Вычисление площади плоскихфигур с помощью определенного
интеграла
Площадь фигуры (S),
ограниченной прямыми х = а
и х = в и графиками
функций у = f(x) и y = g(x),
непрерывных на отрезке
[а;в] и таких, что для любого
хє[а;в] выполняется
неравенство g(x)≤ f(x),
вычисляется по формуле:
46.
bS f ( x) g ( x) dx
a
Например:
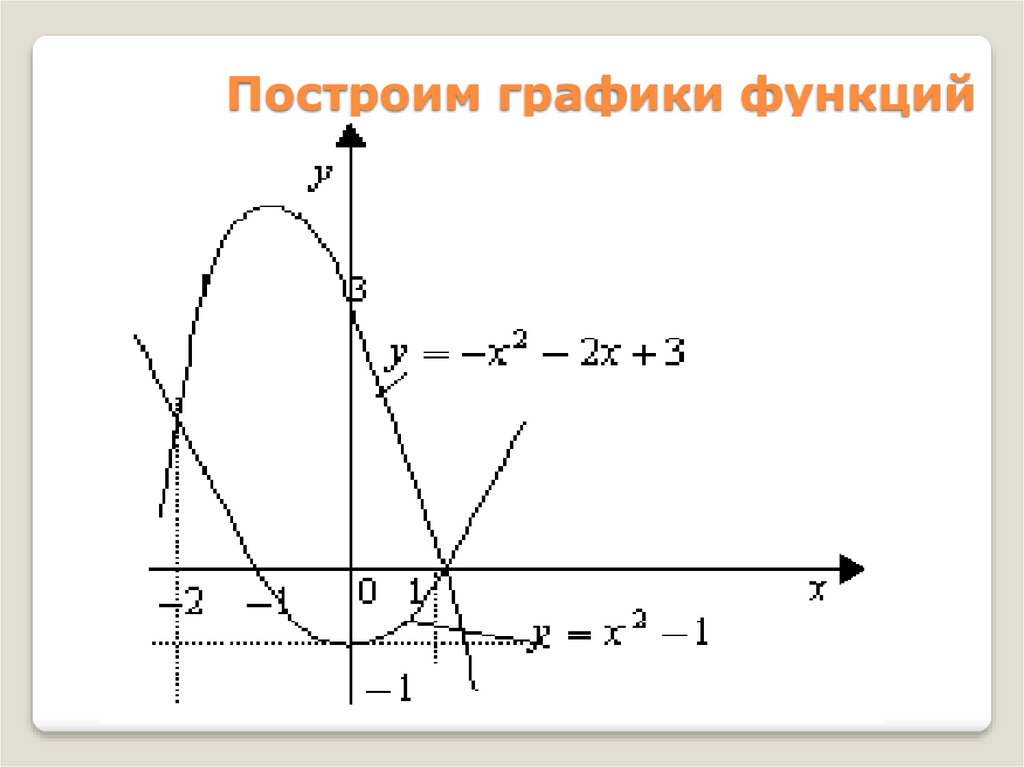
Вычислить площадь фигуры,
ограниченной графиками функций
y x 2x 3
2
y x 1
2
47.
Построим графики функций48.
ЗначитПределы интегрирования: от2 до1
b
f(x)= - x²-2x+3S g(x)=x²
f ( x) g ( x) dx
-1
a
1
Тогда
2
2
S x 2 x 3 x 1 dx
2
1
=
2 x 2 x 4 dx
2
2
49.
12 x x 2 dx
2
=
2
1
x3 x2
2
2x
3
2
2
1 1
8
8 4
1 1
2 2 4 2 2 6
3
3 2
3 2
3 2
1
9
2 3 8 2 9
2
2
50.
ЗапомнимГеометрический
смысл
определенного интеграла –
это площадь
криволинейной трапеции
Физический смысл
определенного интеграла –
это…
(учебник: стр. 291)
51.
Вычисление объема телавращения
Объем тела, образованного
вращением вокруг оси Ox
криволинейной трапеции,
ограниченной кривой
у =f(x) отрезком оси абсцисс a ≤
x≤b
и прямыми x=a;
x=b, вычисляется по формуле
b
Vx π
f
x
2
a
dx
52.
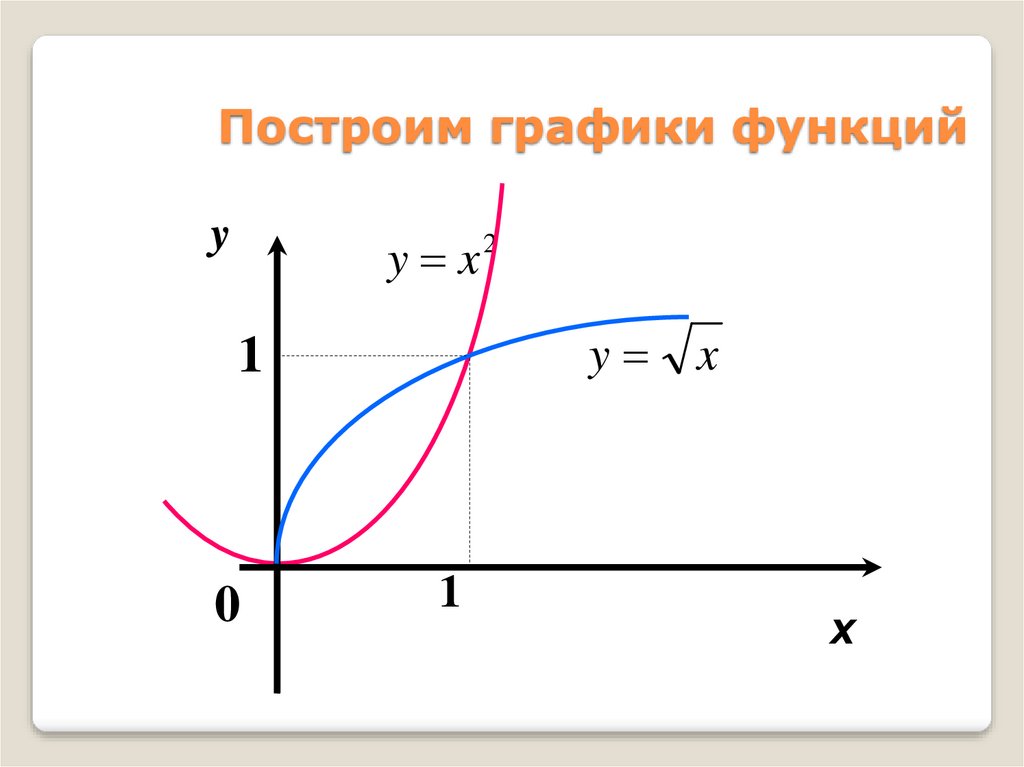
НапримерНайти объем тела,
полученного вращением
вокруг оси Ox
криволинейных трапеций,
ограниченных линиями
у= х² и у = √х
53.
Построим графики функцийy
y x
y x
1
0
2
1
х
54.
РешениеИскомый объем можно
найти как
разность объемов,
полученных
вращением вокруг оси Ox
криволинейных трапеций,
1
1
ограниченных линиями
2
2 2
у=√х и Vx
x dx x dx
у = х². Т.е.:
0
0
55.
11
xdx x dx
4
0
0
2 1
x
2
=
3
2 5 10
0
5 1
x
5
0
56.
Применение интегралаПлощадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Масса
Перемещение
Дифференциальное уравнение
Давление
Количество теплоты
57.
Найти площадь фигуры,ограниченной линиями
1) y=–3x²–2, x=1, x=2,
y=–1
2) у= 4x–x², y=0
3) y= x²–2x+3, x+y=5
4) y=x², y= x
















































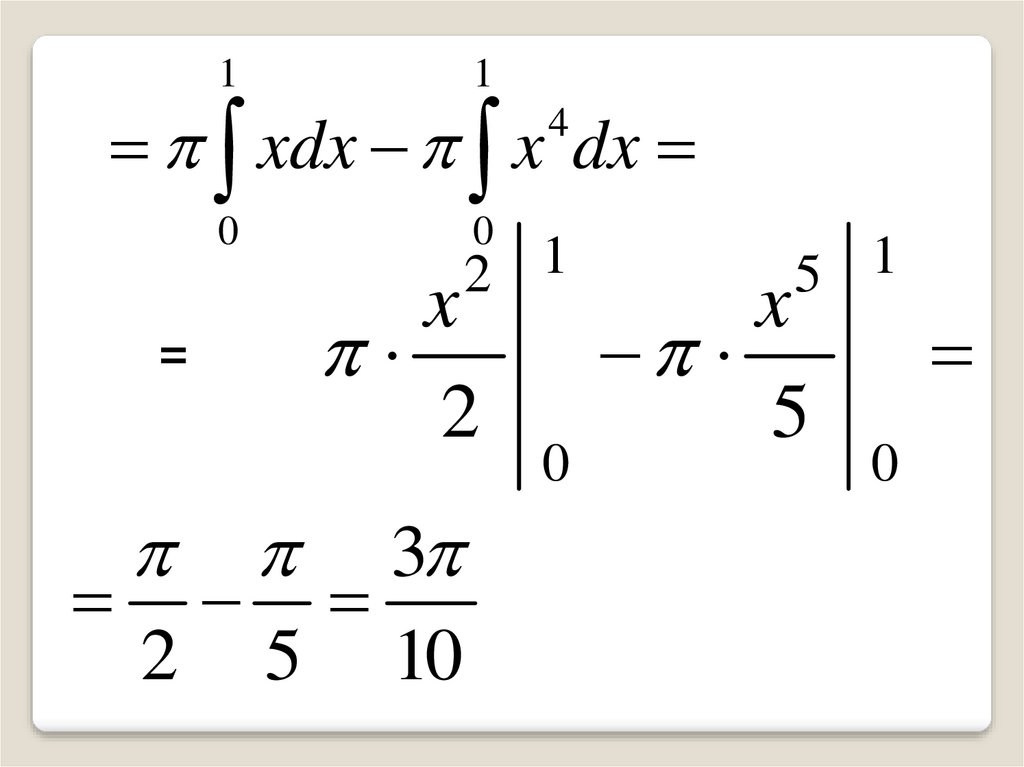


 Математика
Математика








