Модульное программирование в MathCAD

1. Модульное программирование в MathCAD

МОДУЛЬНОЕ
ПРОГРАММИРОВАНИЕ
В
MATHCAD

2.

Сущность и преимущества
модульного программирования
Модульная программа – программа, реализующая алгоритм
вычислений в виде модулей и обращения к ним.
Сущность:
• в разбиении алгоритма решения задачи на слабо зависимые
фрагменты вычислений (на подзадачи) и реализация каждого
фрагмента в виде программных модулей;
• в вызове в нужных местах «основной» программы
соответствующих модулей с передачей необходимых данных.
Преимущества:
• возможность распараллеливания разработки программы;
• простота отладки;
• простота сопровождения и модификации;
• возможность использования библиотек «готовых» модулей.

3.

Описание подпрограммы-функции
ПФ предназначены для многократного выполнения фрагментов программы
без повторения их записи.
имя подпрограммы-функции
Оригинальное имя, используемое для обращения к ПФ и
«возврата» результата ее выполнения.
список формальных параметров
Передает данные, необходимые для выполнения вычислений
внутри ПФ: переменные, массивы, функции.
Формальные параметры заключаются в круглые скобки и
отделяются запятой (список формальных параметров может
отсутствовать).
тело подпрограммы-функции
Включает любое число операторов: локальных операторов
присваивания, условных операторов и операторов цикла, а
также вызовов других ПФ и функций пользователя.

4.

Порядок описания подпрограммы-функции
Ввести имя ПФ и список формальных параметров, заключенный в круглые
скобки.
Ввести символ присваивания «:=».
Открыть панель инструментов Programming (Программирование)
и нажать кнопку Add Line (Добавить линию)
В поле 1 вводится оператор тела ПФ.
Увеличение числа полей для ввода дополнительных операторов осуществляется
с помощью кнопки Add Line или с клавиатуры «]»
Удаление оператора или поля ввода осуществляется нажатием клавиши Delete
Заполнить поле 2 (нижнее поле),
возвращаемое через имя ПФ значение
введя
выражение,
определяющее

5.

Локальный оператор присваивания
<Имя переменной>
<Выражение>
Обращение к подпрограмме функции
< имя П-Ф > (< список фактических параметров >)
Обращение к П-Ф должно находиться после ее описания, и к моменту
обращения фактические параметры должны быть определены.
x 7
f ( x)
x x 2
z x
z
Варианты обращения к ПФ
f ( x) 3
x 7
f ( 5) 2.646
z f ( x 7)
z 4

6.

Программирование линейных алгоритмов
Под линейным алгоритмом понимается вычислительный процесс, в
котором необходимые операции выполняются строго последовательно.
2
root_poly2 ( a b c)
d b 4 a c
root_poly2 ( a b c)
d b
b 4 a dc
x1
b2 a d
b d
x1
x2
2 a
b2 a d
x2
x1 2 a
2
x1
x2
x2
1.25 1.561i
z root_poly2 ( 2 5 8)
1.25 1.561i

7.

Программирование разветвляющихся алгоритмов
В разветвляющихся алгоритмах присутствует
вычислительного процесса. Выбор конкретной
выполнения (или невыполнения) заданных условий.
несколько ветвей
ветви зависит от
Условный оператор if
Условная структура ЕСЛИ- ТО
В поле 2 вводится логическое выражение (выражение отношений).
В поле 1 вводится выражение (как правило, арифметическое), значение
которого используется, если проверяемое логическое выражение
принимает значение 1 (истина)

8.

Программирование разветвляющихся алгоритмов
Условная структура ЕСЛИ- ТО - ИНАЧЕ
ВЫР2 выполняется, если проверяемое логическое выражение (УСЛ) = 0.
Оператор oterwise
оператора if
следует
y( x)
непосредственно
после
ln( x) if x 0
e
y( 3) 0.05
x
otherwise
y( 2.71) 0.997
условного

9.

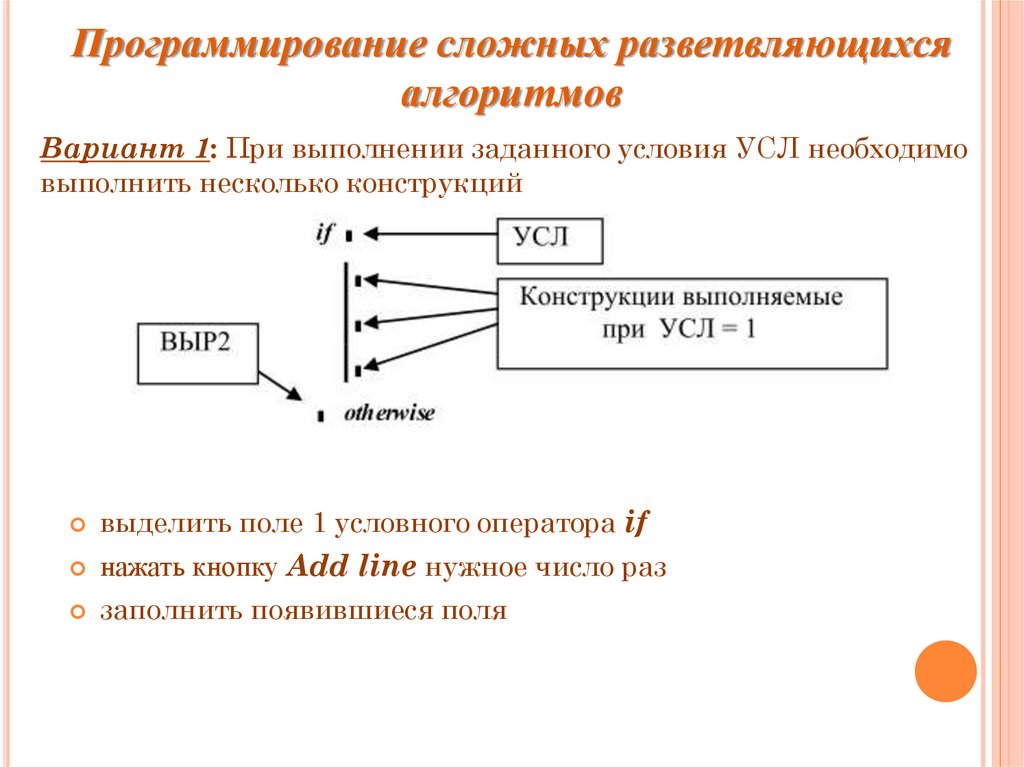
Программирование сложных разветвляющихся
алгоритмов
Вариант 1: При выполнении заданного условия УСЛ необходимо
выполнить несколько конструкций
выделить поле 1 условного оператора if
нажать кнопку Add line нужное число раз
заполнить появившиеся поля

10.

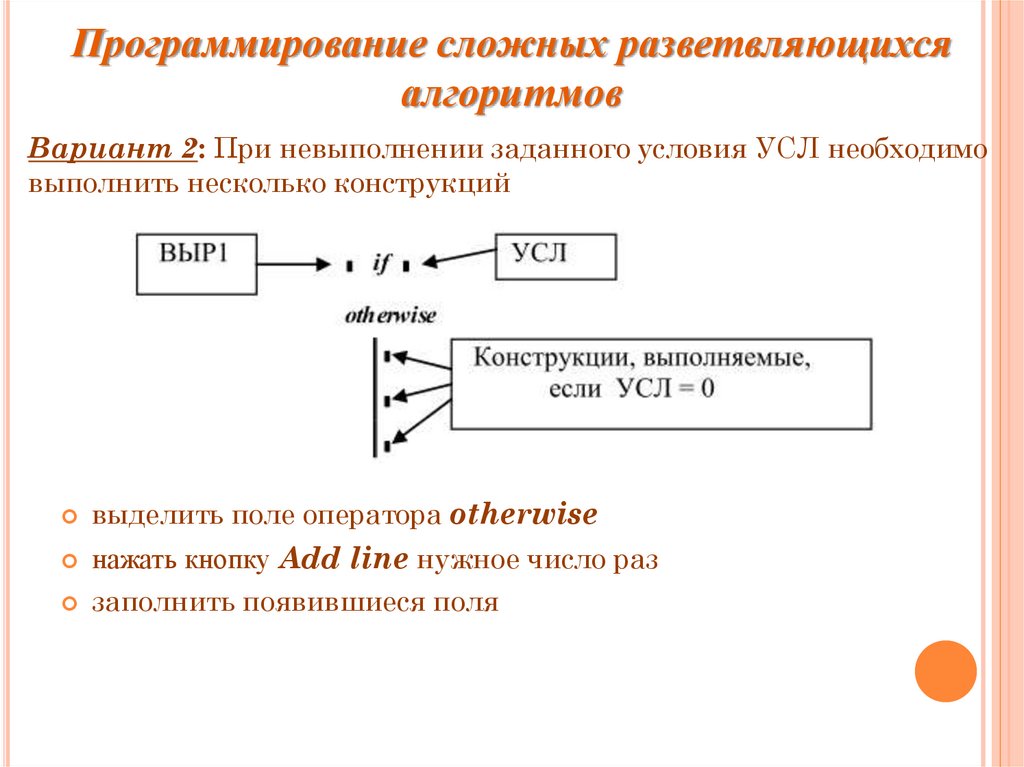
Программирование сложных разветвляющихся
алгоритмов
Вариант 2: При невыполнении заданного условия УСЛ необходимо
выполнить несколько конструкций
выделить поле оператора otherwise
нажать кнопку Add line нужное число раз
заполнить появившиеся поля

11.

Программирование сложных разветвляющихся
алгоритмов
Составить ПФ, возвращающую значения двух переменных a и b,
возведенных во вторую или третью степень. Степень задается
переменной n. Если n < 2 или n > 3, то значения переменных
принять равными 0.
poly( n a b)
if n
2
x a
2
y b
if n
3
x a
3
y b
otherwise
x 0
y 0
x
y
2
3
0
poly( 1 2 3)
0
0
poly( 0 2 3) 0
poly( 0 2 3) 00
poly( 0 2 3) 0
04
poly( 2 2 3) 4
9
poly( 2 2 3) 4
poly( 2 2 3) 9
9
8
poly( 3 2 3)
27

12.

Программирование циклических алгоритмов
Циклические алгоритмы (циклы) содержат повторяющиеся вычисления,
зависящие от некоторой переменной.
Такая переменная называется параметром цикла, а сами
повторяющиеся вычисления составляют тело цикла.
Программирование цикла типа
арифметической прогрессии
Оператор цикла for
В поле 1 вводится имя переменной, являющейся параметром цикла;
В поле 2 вводится закон изменения параметра цикла, используя для
этого описание дискретной переменной или описание массива;
В поле 3 вводятся операторы, составляющие тело цикла.

13.

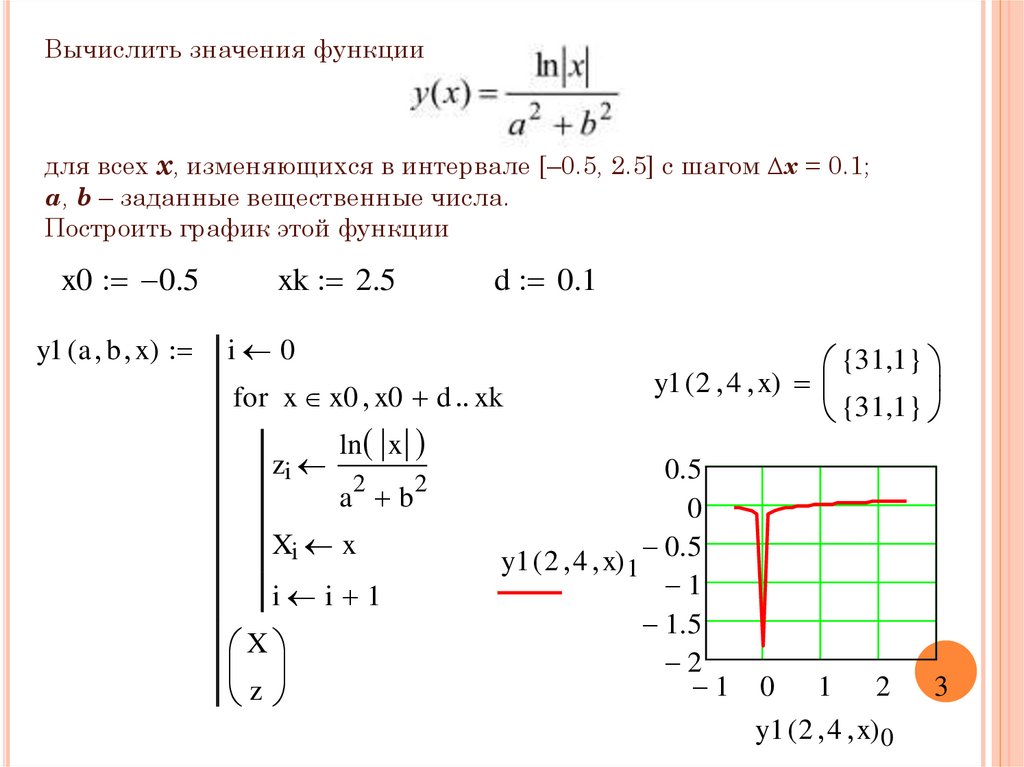
Вычислить значения функции
для всех x, изменяющихся в интервале [–0.5, 2.5] с шагом ∆x = 0.1;
a, b – заданные вещественные числа.
Построить график этой функции
x0 0.5
y1 ( a b x)
xk 2.5
d 0.1
i 0
for x x0 x0 d xk
zi
ln x
2
a b
Xi x
i i 1
X
z
2
{31,1}
y1 ( 2 4 x)
{31,1}
0.5
0
0.5
y1 ( 2 4 x) 1
1
1.5
2
1
0
1
2
y1 ( 2 4 x) 0
3

14.

.
Составить описание П-Ф, вычисляющей сумму вектора с
проекциями |2,5,7|
Составить описание П-Ф, вычисляющей
слагаемых 2, 3, 5, 9, 11, 17, 21.
сумму
следующих

15.

Составить П-Ф, которая формирует двумерный массив из
объектов разных типов.

16.

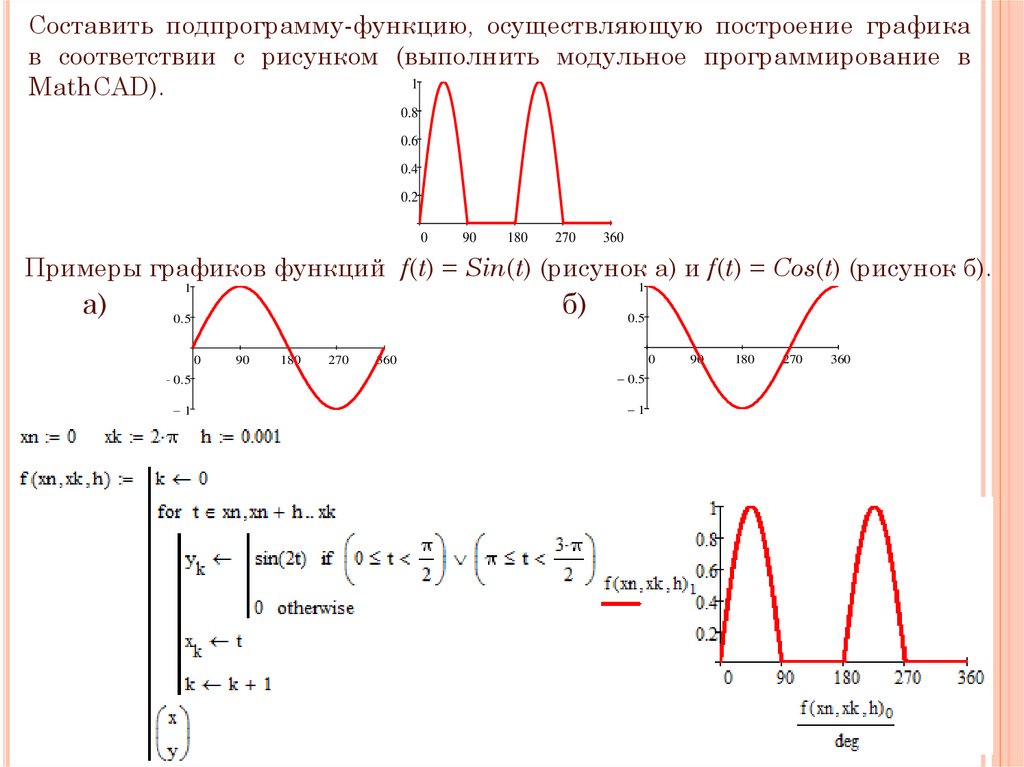
Составить подпрограмму-функцию, осуществляющую построение графика
в соответствии с рисунком (выполнить модульное программирование в
1
MathCAD).
0.8
0.6
0.4
0.2
0
90
180
270
360
Примеры графиков функций f(t) = Sin(t) (рисунок а) и f(t) = Cos(t) (рисунок б).
1
а)
б)
0.5
1
0.5
cos ( t)
sin ( t)
0
90
180
270
0
360
0.5
0.5
1
1
t
deg
90
180
t
deg
270
360

17.

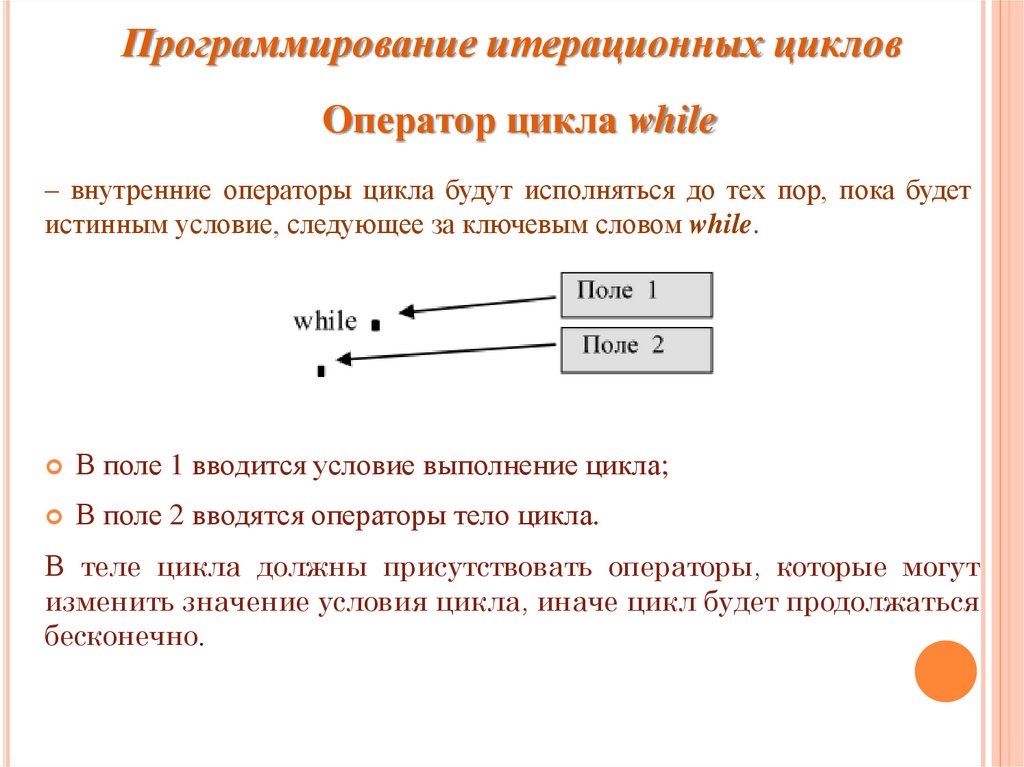
Программирование итерационных циклов
Оператор цикла while
– внутренние операторы цикла будут исполняться до тех пор, пока будет
истинным условие, следующее за ключевым словом while.
В поле 1 вводится условие выполнение цикла;
В поле 2 вводятся операторы тело цикла.
В теле цикла должны присутствовать операторы, которые могут
изменить значение условия цикла, иначе цикл будет продолжаться
бесконечно.

18.

Решить методом Ньютона
1.2. Решение методом Ньютона
2
f ( x) 5 sin( x) 4 x 5.8
100
root_Nyuton
10
f ( t)
5
0
100
5
10
df ( x)
d
f ( x)
dx
x0 3 x1 x0
400
t
x0 3
i 1
200
300
4
10
while xi xi 1
xi 1 xi
f x0
df x0
f xi
df xi
i i 1
x
T
root_Nyuton ( 3 1.9811938 1.6833021 1.6429796 1.6421985 1.6421982 )

19.

Программирование итерационных циклов
Оператор break
– служит для преждевременного завершения цикла, чтобы,
например, избежать зацикливания или слишком продолжительных
вычислений.
Оператор break используется в левом поле ввода условного
оператор if, а в правом размещается условие, при выполнении
которого происходит прекращение работы цикла или программы.

20.

ierr 0
root_Nyut ( x0 )
ierr 1 x0 x0
df ( x)
break
xi 1 xi
f xi
df xi
d
f ( x)
dx
x "not solve" if ierr
1
f x0 x
x1 x0
ierr
df x0
for i 1 5
if
xi xi 1
ierr 0
T
4
root_Nyut 3 10
break
xi 1 xi
f xi
df xi
x "not solve" if ierr
x
ierr
3
1.9811938
1.6833021
0
1.6429796
1.6421985
1.6421982
1
3 T
10
root_Nyut 3 10
1.981
solve" 1 )
( "not

21.

Программирование двойных циклов
Сформировать матрицу (двумерный массив) В по следующему
правилу:
ORIGIN 1
form_M( n m)
for i 1 n
for j 1 m
Bi j
B
1
i j 1
0.333 0.25
0.25
0.2
form_M( 4 2)
0.2 0.167
0.167 0.143

22.

Дополнительные операторы, используемые
при программировании циклов
Оператор continue
Обычно используется для продолжения выполнения цикла путем
возврата в начало тела цикла
Составить описание П-Ф, формирующую новый
положительных элементов исходного вектора.
form_V ( v)
i 0 j 0
while i last ( v)
i i 1
continue if vi 0
j j 1
wj vi
w
2
6
v 1
12
5
вектор
2
form_V ( v) 12
5
из

23.

Оператор return
– преждевременное завершение ПФ и возвращение операнда,
стоящего в поле 1
f ( x)
y x
2
f ( x)
z y 1
return z
y x
2
z y 1
f ( 2) 5
z
Составить описание П-Ф, находящую первую положительную проекцию
исходного вектора.
pol_1 ( v)
i 1
while vi 0
i i 1
vi
pol_1 ( v) 2
pol_2 ( v) for i 1 last ( v)
return vi if vi 0
pol_2 ( v) 2

24.

Оператор on error
– перехват ошибок.
< конструкция 1 > on error < конструкция 2 >
В поле 2 вносится выражение, ошибка в вычислении которого должна
быть зарегистрирована.
В поле 1 вносится условие, которое необходимо выполнить при
возникновении ошибки.

25.

Функция error
Используется для вывода диагностических сообщений
возникновении в вычислениях ошибки и записывается в виде
при
error ("< диагностическое сообщение пользователя >")
Сформировать вывод диагностического сообщения
спроецировать вектор v на нулевой вектор w
при
попытке