Электромагнитные колебания. Превращение энергии в колебательном контуре

1. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ ПРЕВРАЩЕНИЕ ЭНЕРГИИ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

L
C

2.

Немецкий учёный Гельмгольц Г.Л..
Занимался проблемами
электродинамики, создал
колебательный контур, состоящий из
катушки индуктивностью L и
конденсатора ёмкостью С.
Гельмгольц Герман Людвиг
1821–1894 гг.

3.

Осциллограф – прибор, который
позволяет обнаружить наличие
колебаний.

4.

График напряжения, подаваемого на
вертикально отклоняющие пластины трубки
U
0
t

5.

C
L
Система, в которой могут осуществляться свободные
электромагнитные колебания, называется колебательным
контуром..
Колебательный контур это электрическая цепь, состоящая
из конденсатора емкостью С и катушки индуктивностью L.

6.

q, i
Электромагнитные колебания
T
q
i
T
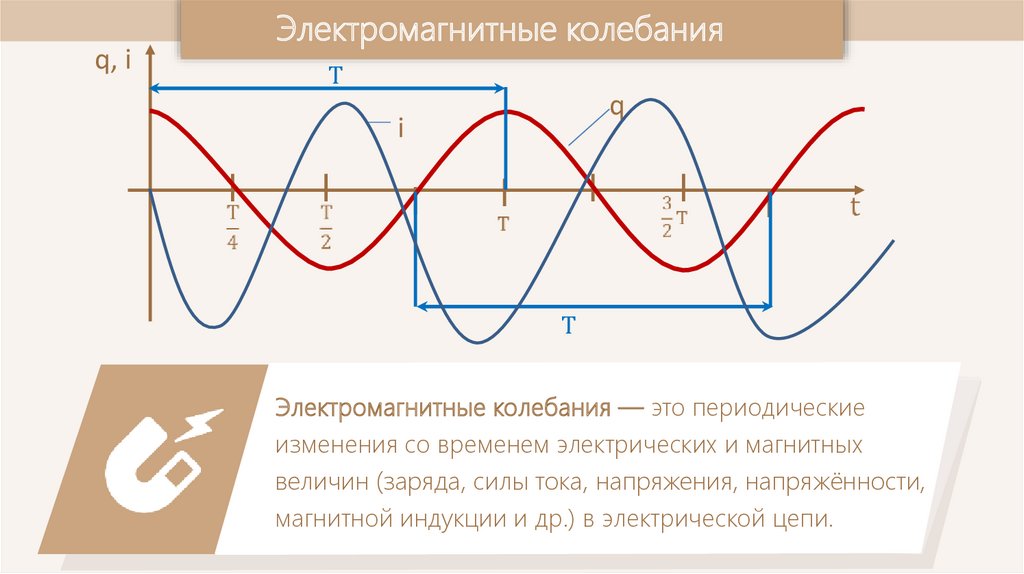
Электромагнитные колебания — это периодические
изменения со временем электрических и магнитных
величин (заряда, силы тока, напряжения, напряжённости,
магнитной индукции и др.) в электрической цепи.

7.

Свободные колебания
+ + ++
- - - -
Свободными колебаниями называются колебания,
которые возникают в системе, выведенной из
состояния равновесия, только за счёт внутренних сил.

8.

+
1
-q
q
C
R
K
2
L
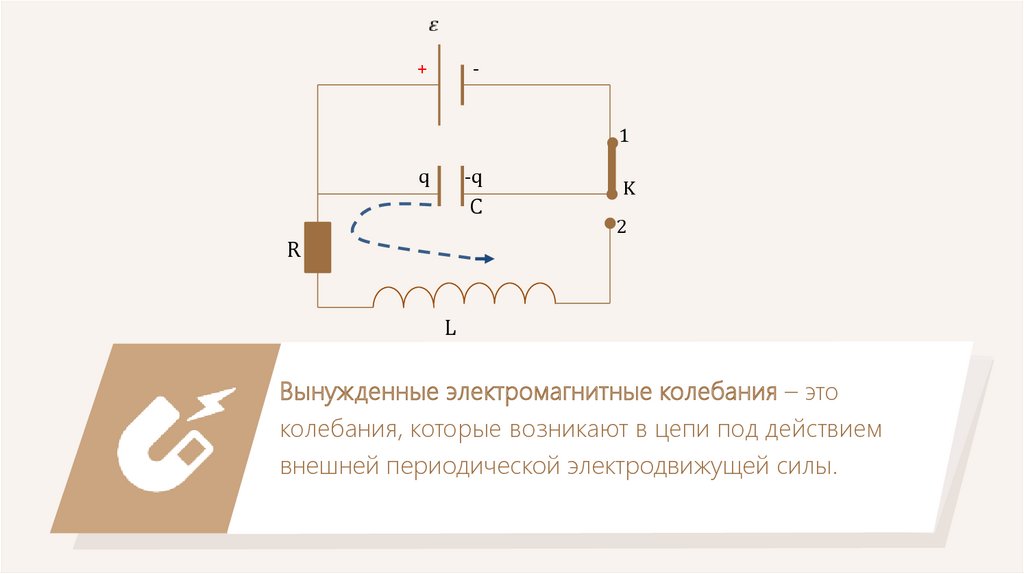
Вынужденные электромагнитные колебания – это
колебания, которые возникают в цепи под действием
внешней периодической электродвижущей силы.

9.

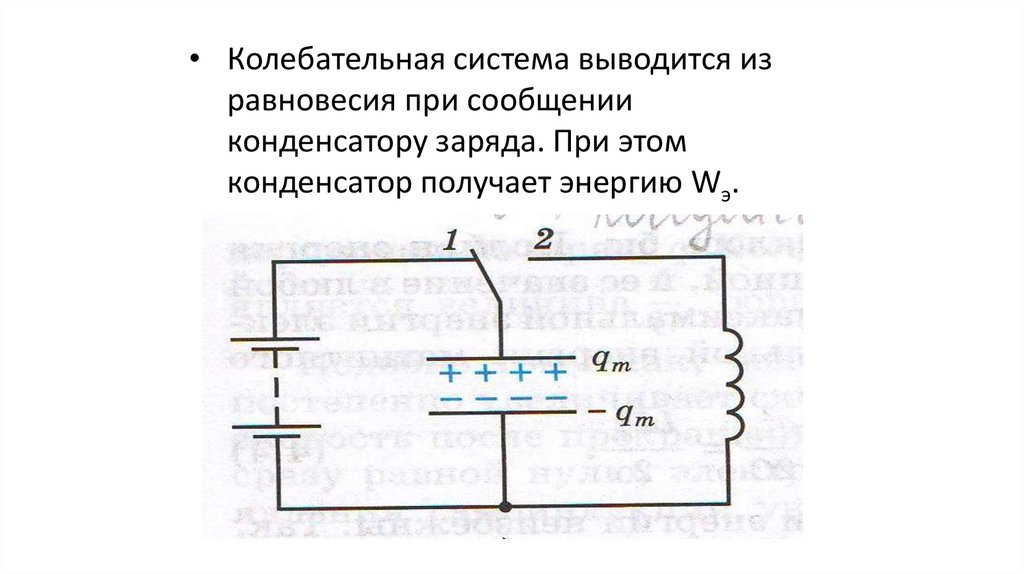
• Колебательная система выводится из
равновесия при сообщении
конденсатору заряда. При этом
конденсатор получает энергию Wэ.

10.

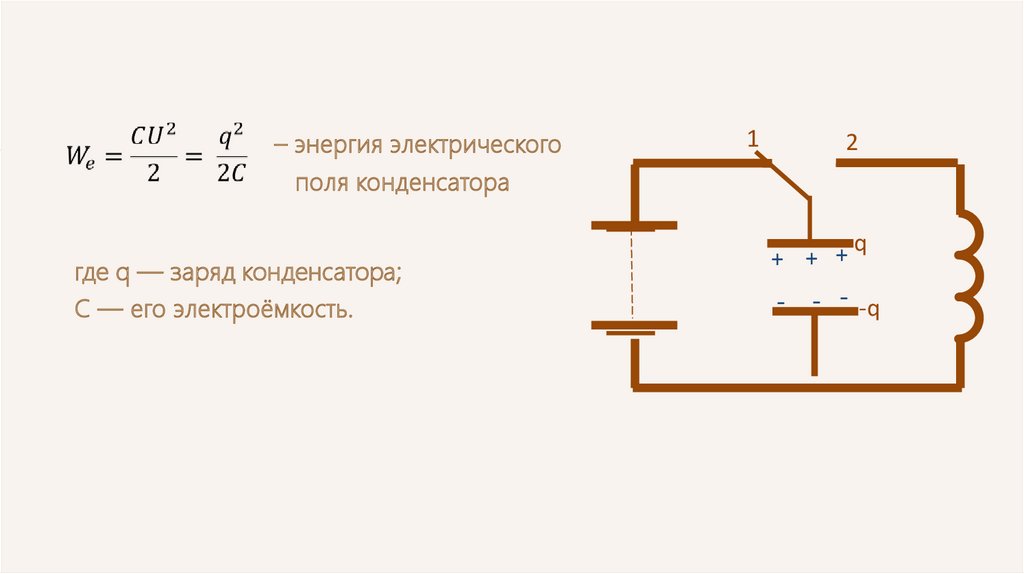
– энергия электрического
поля конденсатора
где q — заряд конденсатора;
С — его электроёмкость.
1
2
q
+ + +
- - - -q

11.

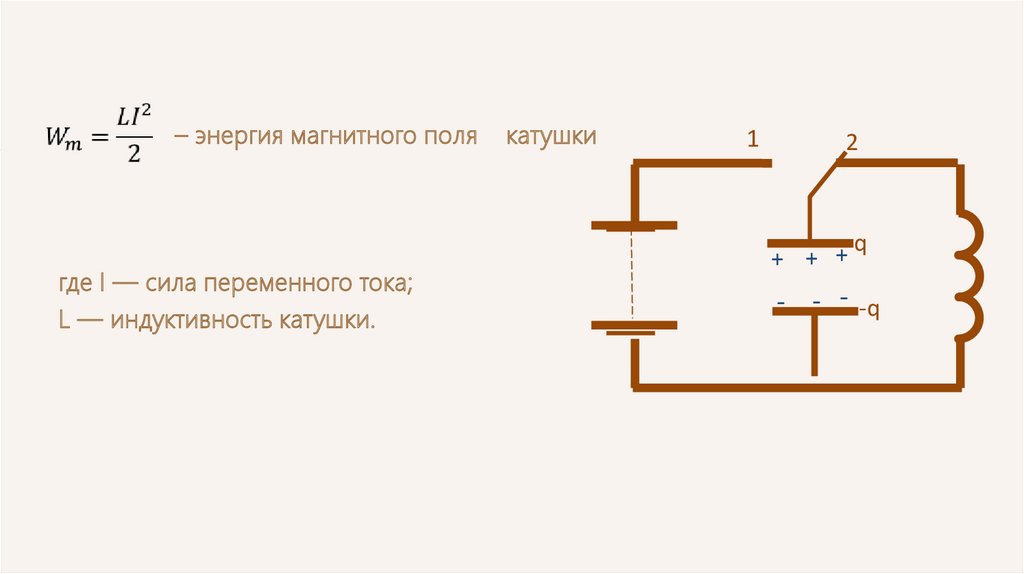
– энергия магнитного поля
где I — сила переменного тока;
L — индуктивность катушки.
катушки
1
2
q
+ + +
- - - -q

12.

Полная энергия электромагнитного
Поля в колебательном контуре

13.

В момент, когда конденсатор полностью
разрядится, энергия электрического поля станет
равной нулю. Энергия же магнитного поля тока,
согласно закону сохранения энергии, будет
максимальной. В этот момент сила тока также
достигнет максимального значения.
C
L
R

14.

В колебательном контуре энергия электрического
поля заряженного конденсатора периодически
превращается в энергию магнитного поля тока.

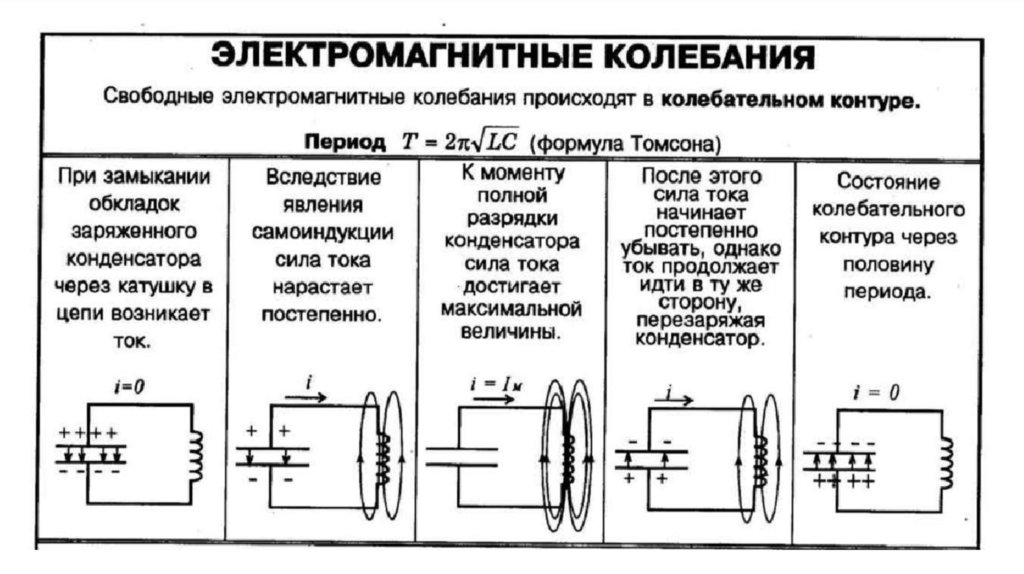
15. Превращение энергии в колебательном контуре

16.

Конденсатор
+
L
+
C
I
Ii
Начальное состояние
Конденсатор заряжен
-
-
+
Конденсатор
разряжается
Конденсатор
разряжается, ток
самоиндукции течет по
катушке
-
+
I
Ii
Конденсатор
перезарядился
Конденсатор
перезарядился
Конденсатор
разряжается, ток
самоиндукции течет по
катушке
+
Конденсатор
разряжается

17.

По мере разрядки конденсатора
энергия электрического поля Wэ
уменьшается, так как уменьшается
заряд на обкладках конденсатора,
но одновременно возрастает
энергия магнитного поля тока Wм.
Полная энергия W
электромагнитного поля контура
равна сумме его энергий магнитного
Wм и электрического Wэ полей.

18.

В момент, когда конденсатор полностью
разрядится, энергия электрического поля
станет равна нулю (так как заряд конденсатора
равен нулю). Энергия магнитного поля станет
максимальной (по закону сохранения энергии).
В этот момент сила тока в цепи становится
максимальной. А раз в цепи есть ток, то
конденсатор начинает опять заряжаться.
Здесь же следует отметить, что сила тока в цепи
поддерживается ЭДС самоиндукции и без
источника тока.

19.

После зарядки конденсатор опять
начинает разряжаться и все происходит
сначала.
Если бы не было потерь энергии, то
колебания в колебательном контуре
были бы незатухающими.
В колебательном контуре энергия
электрического поля заряженного
конденсатора периодически
переходит в энергию магнитного
поля тока.

20.

Qm
+
0
0
q
+
+
q
Im
i
i
+
Qm
0
+
q
0
Im
i
1
2
3
4
5
6
7
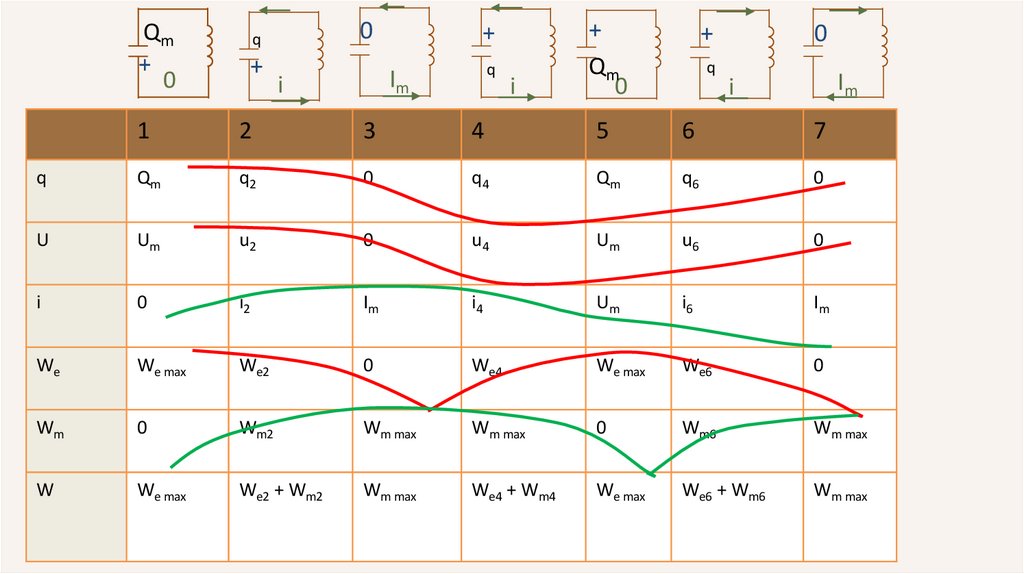
q
Qm
q2
0
q4
Qm
q6
0
U
Um
u2
0
u4
Um
u6
0
i
0
i2
Im
i4
Um
i6
Im
We
We max
We2
0
We4
We max
We6
0
Wm
0
Wm2
Wm max
Wm max
0
Wm6
Wm max
W
We max
We2 + Wm2
Wm max
We4 + Wm4
We max
We6 + Wm6
Wm max

21.

22.

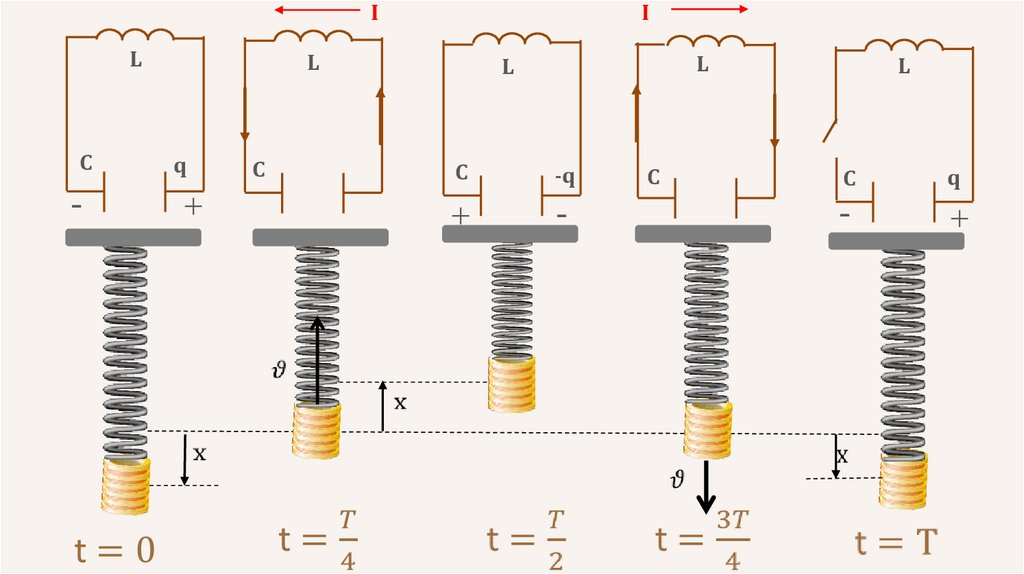
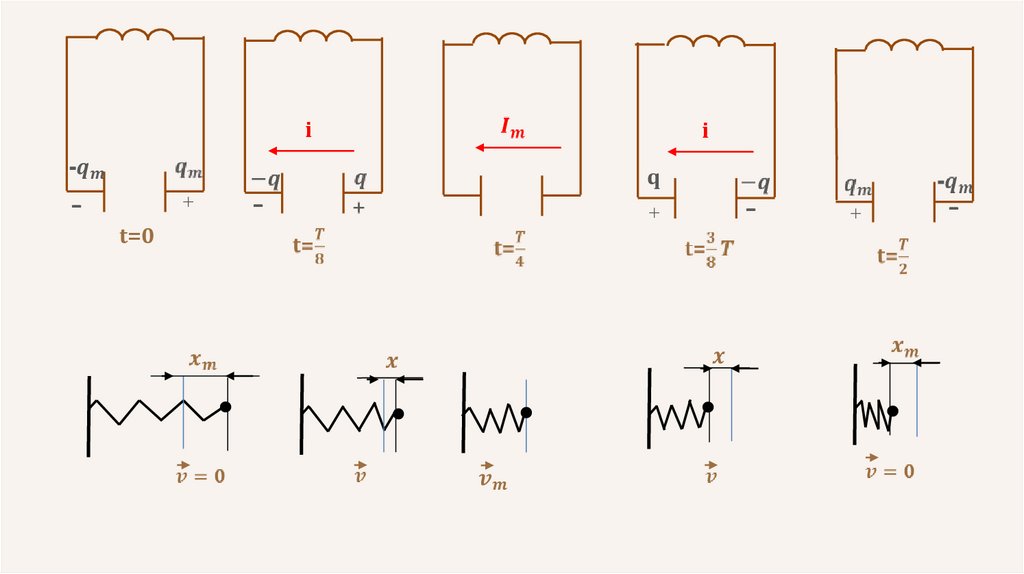
• Аналогия электромагнитных колебаний в
колебательном контуре с механическими
колебаниями пружинного маятника и
математического маятника

23.

I
L
C
-
I
L
q
+
C
L
L
C
+
-q
-
C
L
C
-
q
+

24.

i
-
+
t=0
-
i
q
+
-
+
-

25.

I
L
C
-
I
L
q
+
C
L
L
C
+
q
-
C
L
C
-
q
+

26.

Сравнительная таблица
механических и электромагнитных колебаний
Механические колебания
Параметры
колебательной
системы
Энергия
Циклическая частота
Величина,
характеризующая
отклонение
Величины,
характеризующие
скорость изменения
состояния
колебательной системы
Масса груза m
Жёсткость пружины k
Электромагнитные колебания

27.

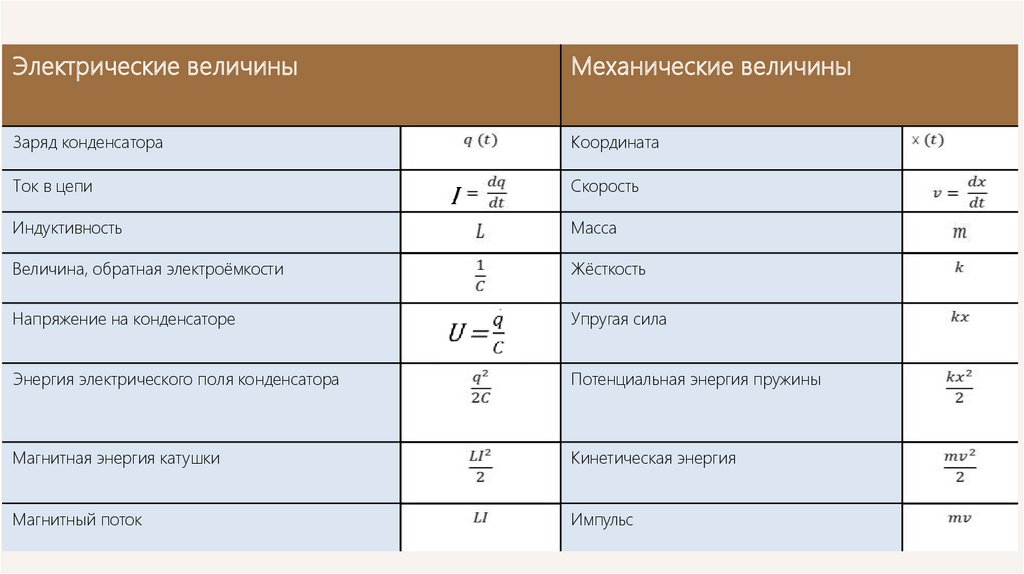
Электрические величины
Механические величины
Заряд конденсатора
Координата
Ток в цепи
I
Скорость
Индуктивность
Масса
Величина, обратная электроёмкости
Жёсткость
Напряжение на конденсаторе
Упругая сила
Энергия электрического поля конденсатора
Потенциальная энергия пружины
Магнитная энергия катушки
Кинетическая энергия
Магнитный поток
Импульс

28.

Уравнение, описывающее свободные
электрические колебания в контуре
+

29.

Уравнение, описывающее свободные
электрические колебания в контуре

30.

Физический смысл полученного уравнения
состоит в том, что скорость изменения энергии
магнитного поля по модулю равна скорости
изменения энергии электрического поля; знак
минус указывает на то, что, когда энергия
электрического поля возрастает, энергия
магнитного поля убывает и наоборот. Именно
благодаря этому полная энергия не меняется.

31.

C
L
q

32.

– циклическая частота
пружинного маятника
– циклическая частота свободных
электрических колебаний

33.

Период колебаний груза на пружине:
Период свободных колебаний в
электромагнитном контуре:

34.

Формула Томсона:
У. Томсон (Кельвин)
1824–1907 гг.

35.

Уравнение изменения координаты
со временем

36.

Уравнение изменения заряда конденсатора
со временем

37.

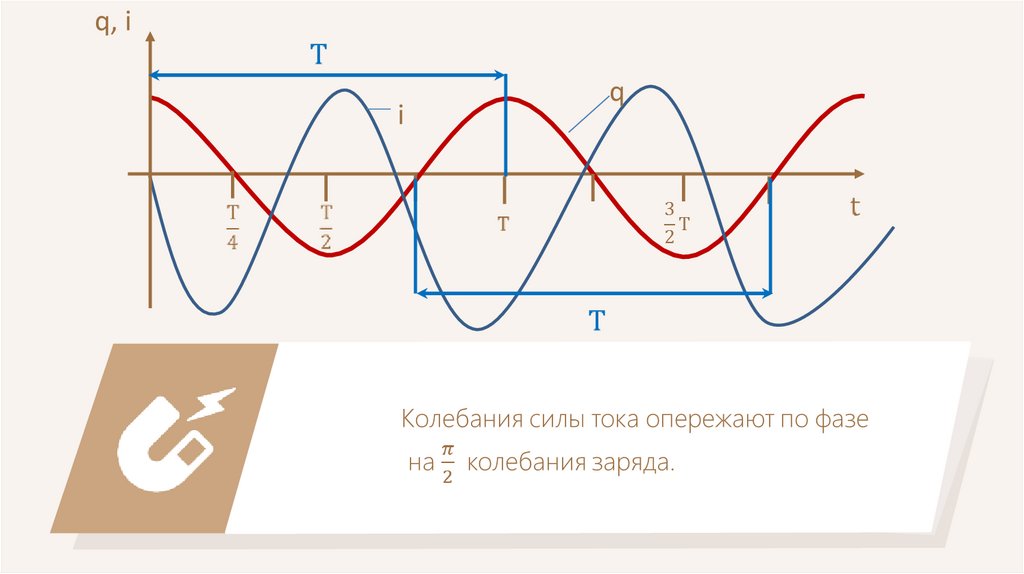
Сила тока совершает гармонические колебания

38.

q, i
i
q

39.

Задача. Колебательный контур состоит из катушки индуктивности и конденсатора.
Индуктивность катушки уменьшили от 32 мГн до 4 мГн. Как и во сколько раз изменится в
результате этого период электромагнитных колебаний в контуре?
Дано:
Решение:
Ответ: в 4 раза увеличится период колебаний,
соответственно в 4 раза уменьшится частота колебаний .

40.

Дано:
Найти: Какую информацию о
колебаниях заряда в контуре
можно получить из этого
уравнения?
Решение: