Логика и алгебра высказываний

1. Математическая логика

2.

Логика - наука о способах доказательств,
которая учит, как надо правильно
рассуждать, оперируя высказываниями
естественного языка

3.

Рассуждать - делать умозаключения на
основании известных фактов, представленных
в виде высказываний:
• «Обычно студентам, не сдавшим вовремя
сессию, не назначают стипендию.
Следовательно, поскольку я не сдал сессию в
срок, я не получу стипендию»;
• «Сумма положительных чисел больше
значения бóльшего из слагаемых. Значит, при
сложении 3 и 4 получится число, большее 3».

4.

Правильно рассуждать - в процессе
формирования умозаключения
использовать верные исходные
высказывания и получать верные новые
высказывания (еще говорят - суждения).
Для этого логика должна содержать
множество правил

5. Задача математической логики -

Задача математической логики организация правильных рассуждений:
оперируя верными высказываниями
естественного языка, правильно делать
умозаключения, получая верные суждения.

6. Определение формальной системы

S=<T, F, A, R>
Т - алфавит (базовые символы);
F - множество формул, построенных из
элементов T с использованием некоторого
набора синтаксических правил, - ППФ;
A F - аксиомы;
R = {ri} - правила вывода:
F1 , F2 ,..., Fn
ri :
или ri : F1 , F2 ,..., Fn G
G
F1 , F2 ,... Fn , G F

7. Структура математической логики

Классическая (истиннозначная) логика:
– Логика высказываний. Предмет исследования –
высказывания, целиком подвергающиеся анализу.
– Логика предикатов. Предмет исследования –
высказывания, элементы (отдельные слова или
словосочетания) которых подвергаются анализу.
– Реляционная логика. Предмет исследования - множества
однородных высказываний, имеющих одинаковую
структуру.
Неклассическая логика:
– Нечёткая логика. Предмет исследования - высказывания,
истинность которых может принимать значения на
континууме.
– Модальная логика. Предмет исследования – высказывания,
отражающие отношение субъекта к истинности или
ложности высказывания.

8. Логика высказываний

9. Предметный язык логики высказываний

1. Алфавит Т:
• обозначения ПП (пропозициональные буквы):
прописные буквы латиницы (за исключением
символов F и G),
• символы операций над высказываниями
(логические связки): , , , , ,
• вспомогательные символы: круглые скобки.
2. Правила F построения ППФ:
• пропозициональные буквы являются формулами F
(элементарными формулами или атомами),
• если F – формула, то F – также формула,
• если F1, F2 – формулы, то F1&F2, F1 F2, F1 F2, F1 F2
– формулы.

10.

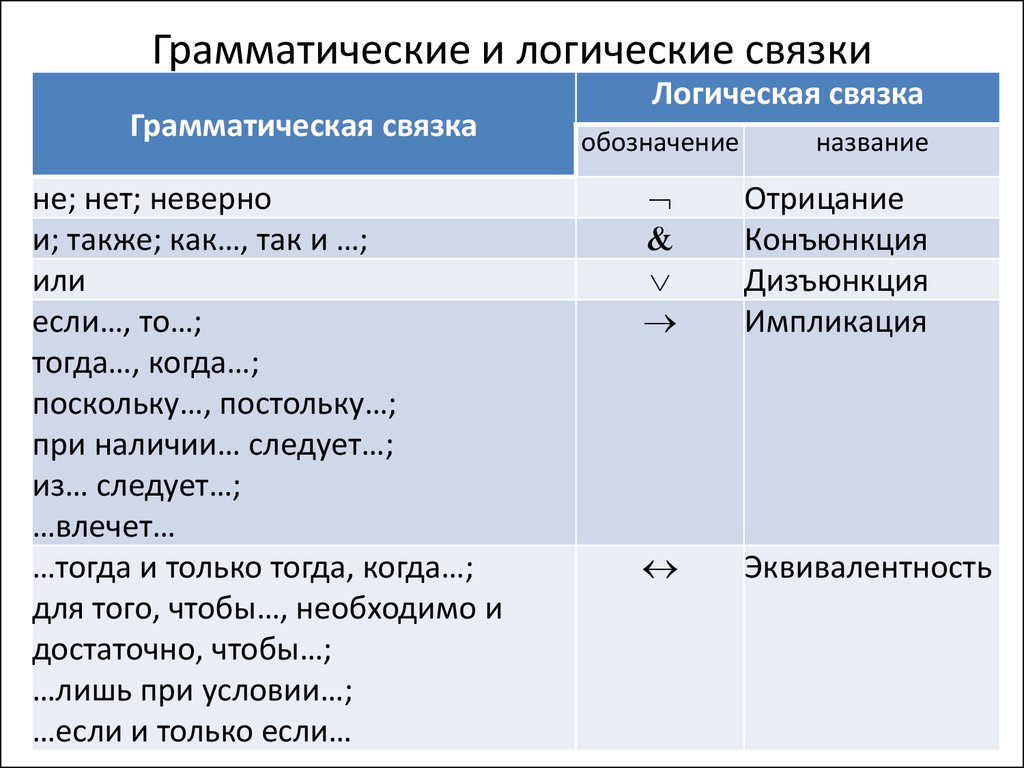
Грамматические и логические связки
Грамматическая связка
не; нет; неверно
и; также; как…, так и …;
или
если…, то…;
тогда…, когда…;
поскольку…, постольку…;
при наличии… следует…;
из… следует…;
…влечет…
…тогда и только тогда, когда…;
для того, чтобы…, необходимо и
достаточно, чтобы…;
…лишь при условии…;
…если и только если…
Логическая связка
обозначение
название
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность

11. Примеры простых и сложных высказываний

ПП
Значение ПП
A
Компьютер – электронное вычислительное устройство
B
Компьютер используется для автоматизации информационных
процессов
C
Винчестер – разновидность внешней памяти компьютера
D
Винчестер входит в состав компьютера
E
Операционные системы – вид прикладного программного обеспечения
H
Винчестер – это вид огнестрельного оружия
А В:= «Компьютер – электронное вычислительное устройство, используемое
для автоматизации информационных процессов»
А:= «Компьютер не является электронным вычислительным устройством»
С D:= «Винчестер является разновидностью внешней памяти компьютера
тогда и только тогда, когда он входит в состав компьютера»
D C:= «Если винчестер входит в состав компьютера, то он является
разновидностью его внешней памяти»
С H:= «Винчестер является разновидностью внешней памяти компьютера или
видом огнестрельного оружия»

12. Практика по формализации сложных высказываний

1. Даны ПП:
• А:=«Компьютер содержит процессор»
• В:=«Компьютер содержит оперативную
память»
• С:=«Компьютер содержит контроллеры»
• D:=«Компьютер содержит порты ввода-вывода»
Задание: формально записать высказывание
«Компьютер содержит процессор, оперативную
память, контроллеры, порты ввода-вывода»
Решение: F=А В С D

13.

2. Даны ПП:
• А:=«По проводнику протекает
электрический ток»
• В:=«Вокруг проводника есть магнитное
поле»
Задание: формально записать высказывание
«Если по проводнику протекает
электрический ток, то вокруг
проводника возникает магнитное поле»
Решение: F=А В

14.

3. Даны ПП:
• А:=«Выполнить загрузку в компьютер
операционной системы»
• В:=«Включить компьютер»
Задание: формально записать высказывание
«Чтобы выполнить загрузку в
компьютер операционной системы,
необходимо и достаточно его включить»
Решение: F=А В

15.

4. Даны ПП:
А:=«подготовка специалистов высокой
квалификации»
С:=«хорошая материальная база»
D:=«обеспечение мотивации студентов и
преподавателей»
Задание: формально записать высказывание
«Подготовка специалистов высокой квалификации
возможна лишь на основе хорошей материальной
базы и обеспечения мотивации студентов и
преподавателей».
Решение:
1) Если есть хорошая материальная база и
обеспечена мотивация студентов и
преподавателей, то возможна подготовка
специалистов высокой квалификации
2) F=C&D А.

16.

5. Дано сложное высказывание: «Хлеба уцелеют в
различных погодных условиях тогда, когда будут
выполнены все мелиоративные работы, а если хлеба
не уцелеют, то фермеры обанкротятся и оставят
фермы».
Задание: дать его формальное описание.
Решение:
1) Если будут выполнены все мелиоративные работы,
то хлеба уцелеют в различных погодных условиях, …
2) Введем обозначения:
«хлеба уцелеют» – A1,
«различные погодные условия» – A2,
«выполнены все мелиоративные работы» – B,
«фермеры обанкротятся» – С1,
«фермеры оставят фермы» – C2,
3) F=(В A1&A2)&( A1 C1&C2).

17.

6. Дано умозаключение: «Если я поеду автобусом и автобус
опоздает, то я опоздаю на занятия. Если я опоздаю на
занятия, то я не сделаю в срок лабораторную работу. Если я
не сделаю в срок лабораторную работу, то я лишусь
стипендии. Следовательно, если я не поеду автобусом, то я
сделаю в срок лабораторную работу и не лишусь стипендии».
Задание: дать его формальное описание.
Решение:
Введем обозначения:
«я поеду автобусом» – A,
«автобус опоздает – B,
«я опоздаю на занятия» – C,
«я лишусь стипендии» – D,
«я сделаю в срок лабораторную работу» – Е,
F ( A & B C ) & (C E ) & ( E D) ( A E & D)

18.

7. Дано умозаключение: «Обвиняемый может быть либо
исполнителем, либо организатором преступления.
Обвиняемый является организатором преступления.
Следовательно, он не является исполнителем
преступления».
Задание: дать его формальное описание.
Решение:
Введем обозначения:
«обвиняемый – исполнитель преступления» – A,
«обвиняемый – организатор преступления» – В.
( A B) & B A

19.

8. Даны высказывания:
A:= «в компьютере применяют матричный
принтер»,
B:= «в компьютере применяют струйный
принтер»,
C:= «в компьютере применяют лазерный
принтер».
Дана формула: F=A B C.
Задание: какое высказывание представляет
данная формула?
Решение:
«В компьютере применяют матричный,
струйный или лазерный принтер».

20.

9. Даны высказывания:
A:= «на упругое тело оказывают влияние
внешние силы»,
B:=«в упругом теле возникают внутренние
силы, препятствующие изменению формы».
Дана формула F=A→B.
Задание: какое высказывание представляет
данная формула?
Решение:
«Если на упругое тело оказывают влияние
внешней силы, то в нем возникают
внутренние силы, препятствующие
изменению формы».

21.

10. Даны высказывания:
A:= «быть четным числом»
B:= «число делится на два».
Дана формула F=A↔B
Задание: какое высказывание представляет
данная формула?
Решение:
«Для того, чтобы число было четным,
необходимо и достаточно, чтобы оно
делилось на два».

22.

11. Даны высказывания:
A:= «урожай будет стабильным ежегодно»
B:= «выполнены все ирригационные работы».
Дана формула F=A↔B
Задание: какое высказывание представляет
данная формула?
Решение:
«Урожай будет стабильным ежегодно тогда и
только тогда, когда будут выполнены все
ирригационные работы».

23. Практика по приоритетам выполнения логических операций

Задание: с помощью скобок указать
последовательность выполнения логических
операций.
Например, дано:
(A B)&(C D)&(B D)&A& D C&B
После введения скобок:
((A B)&(C D)&(B ( D))&A&( D)) (( C)&B)

24.

(B (A C))&(B A)& C& D (B D)
(B A)&(B ( A C))&( С D) B D
(A B)&(C B)&(B D)& D A& C
(A B)&(A (B C))&(B C)& C A& B
(A B)&(C D)&(B D)&C A&D
(A B)&(B (A C))& C A& B
(A B)&(D C)& B& C (A D)
(A B)&(C B)&C& D (A D)
(A B)&( B C)&(A C)&(A B D)& B C D
(A B)&(D C)& (B C) A& D
(A B)& (C B)& (D C)& D A
(A B)& (B D C)&A D C

25. Алгебра высказываний

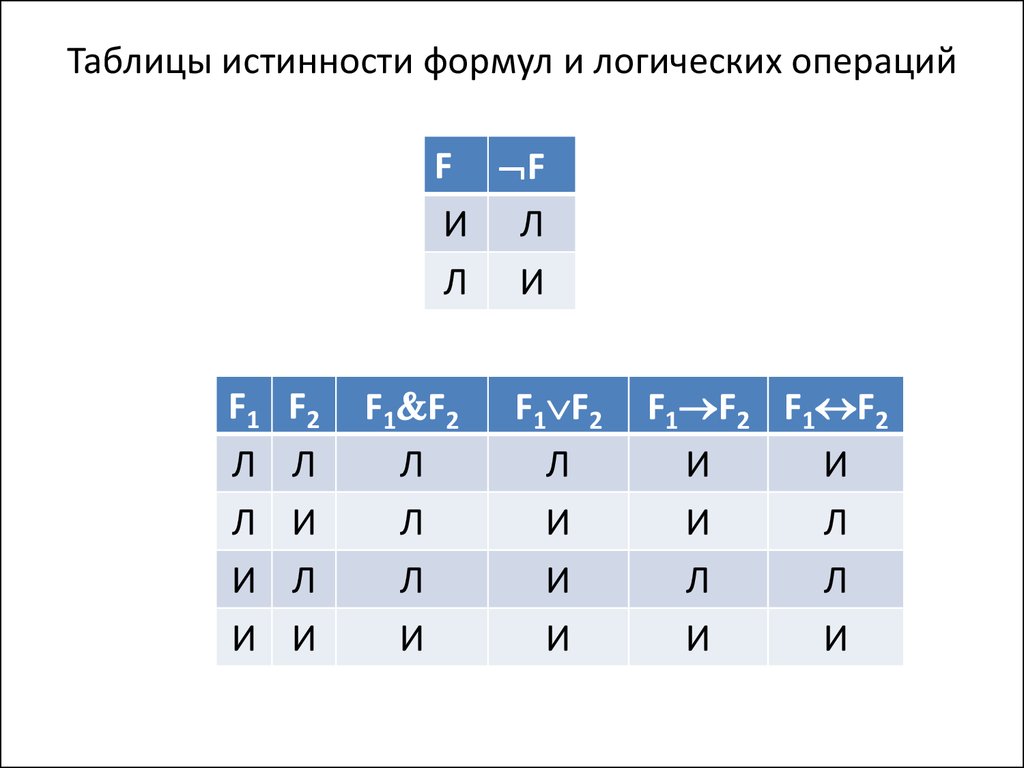
26. Таблицы истинности формул и логических операций

F F
И Л
Л И
F1
Л
Л
И
И
F2
Л
И
Л
И
F1 F2
Л
Л
Л
И
F1 F2
Л
И
И
И
F1 F2 F1 F2
И
И
И
Л
Л
Л
И
И

27. Понятие тавтологии (|= )

Понятие тавтологии (|=)
Тавтология – это формула F, истинная при
всех значениях входящих в нее ПП:
|=F

28. Основные тавтологии ЛВ

1а. |=F1→(F2→F1)
1б. |=(F1 F2) ((F1 (F2 F3)) (F1 F3))
2. |=F1 (F2 F1&F2)
3а. |=F1&F2 F1
3б. |=F1&F2 F2
4а. |=F1 F1 F2
4б. |=F2 F1 F2
5. |=(F1 F3) ((F2 F3) (F1 F2 F3))
6. |=(F1 F3) ((F1 F3) F1)
7. |=(F1 F2) ((F2 F1) (F1 F2))
8а. |=(F1 F2) (F1 F2)
8б. |=(F1 F2) (F2 F1)
9. |=F1 ( F1 F3)

29.

Дополнительные тавтологии ЛВ:
Название
Формула
Коммутативность |=F1 F2 F2 F1
|=F1 F2 F2 F1
|=
F
(F
F
) (F
F
)
F
1
2
3
1
2
3
Ассоциативность
|=F1 (F2 F3) (F1 F2) F3
Дистрибутивность |=F1 (F2 F3) (F1 F2) (F1 F3),
|=F1 (F2 F3) (F1 F2) (F1 F3)
Идемпотентность |=F F F, |=F F F
Исключение
|=F F и
третьего
Противоречие
|=F F л

30. Дополнительные тавтологии (продолжение)

Название
Закон де
Моргана
Формула
|= (F1 F2) F1 F2
|= (F1 F2) F1 F2
Дополнение
|= ( F) F
Закон константы
|= F л F |= F и и
|=F л л |= F и F
Для импликации |=F1 F2 F1 F2
Для
эквивалентности |=(F1 F2) (F1 F2) (F2 F1)

31.

Законы логики высказываний
Имя закона
Коммутативности
Ассоциативности
Равносильные формулы
F1 F2 F2 F1, F1 F2 F2 F1
F1 (F2 F3) (F1 F2) F3,
F1 (F2 F3) (F1 F2) F3
Дистрибутивности
F1 (F2 F3) (F1 F2) (F1 F3),
F1 (F2 F3) (F1 F2) (F1 F3)
Идемпотентности
F F F, F F F
Исключения третьего F F и
Противоречия
F F л
Де Моргана
(F1 F2) F1 F2,
(F1 F2) F1 F2
Дополнения
( F) F
Константы
F л F, F и и, F л л, F и F
Для импликации
F1 F2 F1 F2
Для эквивалентности F1 F2 (F1 F2) (F2 F1)

32. Практика по таблицам истинности

• С помощью таблиц истинности доказать
тавтологии

33. Примеры по эквивалентному преобразованию формул

1. Вывести закон поглощения вида:
|=F1 (F1 F2) F1.
Решение (преобразуем левую часть):
• по закону константы:
(F1&и) (F1&F2)=
• по закону дистрибутивности:
F1&(и F2)=
• по закону константы:
F1

34.

2. Вывести закон поглощения вида:
|=F1 (F1 F2) F1.
Решение (преобразуем левую часть):
• по закону константы:
(F1 л)&(F1 F2)=
• по закону дистрибутивности:
F1 (л&F2)=
• по закону константы:
F1

35.

3. Вывести закон Порецкого вида:
|=F1 ( F1 F2) F1 F2.
Решение (преобразуем левую часть):
• по закону дистрибутивности:
(F1 F1) (F1 F2)=
• по закону исключения третьего:
и (F1 F2)=
• по закону константы:
F1 F2

36.

4. Вывести закон Порецкого вида:
|=F1 ( F1 F2) F1 F2.
Решение (преобразуем левую часть):
• по закону дистрибутивности:
(F1& F1) (F1&F2)=
• по закону противоречия:
л (F1&F2)=
• по закону константы:
F1&F2

37.

5. Вывести закон обобщенного склеивания вида:
|=F 1 F2 F1 F2 F1 F2 F1 F2 F2
Решение:
1) преобразуем правую часть тождества:
• по закону константы:
F1 F2 F1 F2 и&F2=
• по закону дистрибутивности:
F2&(F1 F1 и)=
• по закону константы:
F2&и=F2
2) преобразуем левую часть тождества:
• по закону дистрибутивности:
F2&(F1 F1)=
• по закону исключения третьего:
F2&и=
• по закону константы:
F2
3)сравним полученные результаты в шагах 1 и 2:
F2=F2

38.

6. Упростить формулу
(F1 F2) ( F3 F4) (F1 F2) (F3 F4).
Решение:
• удалим :
( F1 F2) ( F3 F4) (F1 F2) (F3 F4)
• по закону де Моргана:
(F1 F2) ( F3 F4) ( F1 F2) ( F3 F4)
• по закону дистрибутивности:
( F3 F4) ((F1 F2) ( F1 F2))
• по закону дистрибутивности: ( F3 F4) F2 (F1 F1)
• по закону исключенного третьего: ( F3 F4) F2 и
• по закону констант:
( F3 F4) F2.

39. Алгоритм приведения к нормальной форме

1. Устранить всюду связки и по законам для
импликации и для эквивалентности:
• F1 F2 = F1 F2
• F1 F2 = (F1 F2) (F2 F1)
2. Используя законы дополнения и де Моргана,
продвинуть отрицание до ПП:
• ( F)=F,
• (F1 F2)= F1 F2
• (F1 F2)= F1 F2
3. Применить закон дистрибутивности:
• для КНФ
F1 (F2&F3)=(F1 F2)&(F1 F3)
• для ДНФ
F1&(F2 F3 )=(F1&F2) (F1&F3)

40. Алгоритм преобразования ДНФ к виду СДНФ

1. Если в элементарную конъюнкцию F не
входит подформула Fi или Fi , то шаг 2.
Иначе – конец.
2. Дополнить элементарную конъюнкцию
формулой (Fi Fi) и выполнить
преобразование формулы по закону
дистрибутивности:
F&(Fi Fi)=(F&Fi) (F& Fi)
3. Повторить шаг 1.

41. Алгоритм преобразования КНФ к виду СКНФ

1. Если в элементарную дизъюнкцию F не
входит подформула Fi или Fi , то шаг 2.
Иначе – конец.
2. Дополнить элементарную дизъюнкцию
формулой (Fi& Fi) и выполнить
преобразование формулы по закону
дистрибутивности F (Fi Fi)=(F Fi) (F Fi).
3. Повторить шаг 1.

42. Алгоритм получения СДНФ по таблице истинности формулы F

• записать конъюнкты, каждый из которых
соответствует одному из истинных
значений формулы F, причем:
ПП включать в конъюнкт с отрицанием,
если она имеет значение «л»,
ПП включать в конъюнкт без отрицания –
в противном случае;
• соединить конъюнкты дизъюнкцией.

43. Пример получения СДНФ по таблице истинности

№
строки
1
2
3
4
5
6
7
8
А
л
л
л
л
и
и
и
и
В
л
л
и
и
л
л
и
и
С
л
и
л
и
л
и
л
и
F
и
л
л
и
л
л
л
и
F=( А& В& C)1
( А&B&C)4 (A&B&C)8

44. Алгоритм получения СКНФ по таблице истинности формулы F

• записать дизъюнкты, каждый из которых
соответствует одному из ложных значений
формулы F, причем:
ПП включать в дизъюнкт с отрицанием,
если она имеет значение «и»,
ПП включать в дизъюнкт без отрицания –
в противном случае;
• соединить дизъюнкты конъюнкцией.

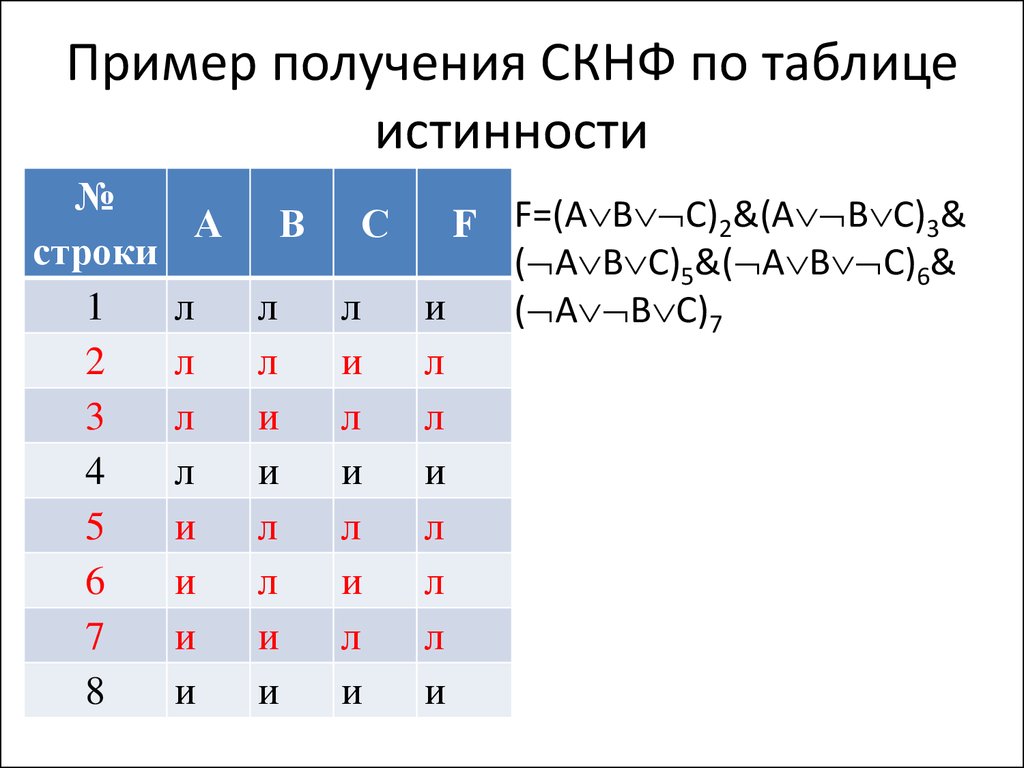
45. Пример получения СКНФ по таблице истинности

№
строки
1
2
3
4
5
6
7
8
А
л
л
л
л
и
и
и
и
В
л
л
и
и
л
л
и
и
С
л
и
л
и
л
и
л
и
F F=(А В C)2&(А B C)3&
( A B C)5&( A B C)6&
и
( A B C)7
л
л
и
л
л
л
и

46. Практика по нормальным формам

1. Преобразовать к виду КНФ
(F1 (F2 F3)) F4
Решение:
• удалим :
( F1 (F2 F3)) F4
• по закону де Моргана:
(F1 F2 F3) F4
• по закону дистрибутивности:
(F1 F4)&( F2 F4) (F3 F4).

47.

2. Преобразовать к виду КНФ :
((A B) (C A)) ( B C)
Решение:
• удалим :
( ( A B) ( C A)) (B C)=
• по закону де Моргана:
((A& B) ( C A)) (B C)=
( (A& B)& ( C A)) (B C))=
( A B)&C&A B C=
• по закону дистрибутивности:
A&C&A B&C&A B C=
• по законам противоречия и дистрибутивности:
B&C&A B C=
(B B C)&(C B C)&(A B C)=
• по законам идемпотентности и исключенного третьего:
(B C)&(A B C)=
• по закону поглощения:
(B C).

48.

3. Преобразовать к виду ДНФ:
((((A B) A) B) C) C
Решение:
• устраним :
( ( ( ( A B) A) B) C) C,
• по закону де Моргана:
( ( ((A& B) A) B) C) C=
• по законам дистрибутивности, исключения третьего, константы:
( ( ((A A)&( B A)) B) C) C=
( ( ( B A) B) C) C=
• по закону де Моргана:
( ((B&A) B) C) C=
• по законам дистрибутивности, исключения третьего, константы:
( ((B B)&(A B)) C) C=
( ( (A B) C) C=
• по закону де Моргана:
(( A&B) C) C=
( ( A&B)&C) C=
(A B)&C C=
• по закону дистрибутивности:
A&C B&C C=
• по закону поглощения:
С

49.

4. Преобразовать к виду ДНФ :
(A (B C)) ((A C) (A B)).
Решение:
• устраним :
( A ( B C)) ( ( A C) ( A B)),
• по закону де Моргана:
(A& ( B C)) A&C ( A B)=
(A&B& C) (A&C) A B.

50.

5. Преобразовать к виду КНФ :
(A&(B C)) ((A&B) C).
Решение:
• устраним :
(A&(B C)) ((A&B) C),
• по законам дистрибутивности,
идемпотентности и поглощения:
A&B A&C A&B C=A&B C,
• по закону дистрибутивности:
(A C)&(B C).

51.

6. Преобразовать к виду КНФ :
(С A) ( (B C) A).
Решение:
• устраним :
( С A) ((B C) A)
• по закону де Моргана:
(C& A) B C A,
• по законам дистрибутивности,
идемпотентности и исключения третьего:
(C B C A)&( A B C A)=(A B C).

52.

7. Преобразовать к виду СДНФ:
(A&¬В)∨(A&¬C&D).
Решение:
(A&¬B&(C∨¬C))∨(A&¬C&D&(B∨¬B))=
(A&¬B&C)∨(A&¬B&¬C)∨(A&B&¬C&D)∨
(A&¬B&¬C&D)=
(A&¬B&C&(D∨¬D))∨(A&¬B&¬C&(D∨¬D))∨
(A&B&¬C&D)∨(A&¬B&¬C&D)=
(A&¬B&C&D)∨(A&¬B&C&¬D)∨(A&¬B&¬C&D)∨
(A&¬B&¬C&¬D)∨(A&B&¬C&D)∨ (A&¬B&¬C&D)

53.

8. Преобразовать к виду СКНФ:
(A∨B)&(¬A∨¬B∨C∨D).
Решение:
(A∨B∨С&¬С)&(¬A∨¬B∨C∨D)=
(A∨B∨C)&(A∨B∨¬C)&(¬A∨¬B∨С∨D)=
(A∨B∨С∨D&¬D)&(A∨B∨¬C∨D&¬D)&
(¬A∨¬B∨С∨D)=
(A∨B∨С∨D)&(A∨B∨С∨¬D)&(A∨B∨¬С∨D)&
(A∨B∨¬С∨¬D)&(¬A∨¬B∨С∨D)