Похожие презентации:
Использование приема аналогии в процессе развития мышления учащихся
1.
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего
образования
«Владимирский государственный университет имени Александра Григорьевича и
Николая Григорьевича Столетовых»
(ВлГУ)
Кафедра «Педагогика и психология дошкольного и начального образования»
ПРЕЗЕНТАЦИЯ по теме:
«Использование приема аналогии в процессе развития мышления
учащихся. Примеры умозаключений по аналогии, которые можно
использовать при изучении математических понятий в 1-4 классах.
Типичные ошибки в вычислениях, которые допускают учащиеся начальных
классов при необоснованном использовании приема аналогии»
Выполнила:
студентка группы НОЛ-118
очной формы обучения
Чулкова Кристина Евгеньевна
Проверила:
старший преподаватель
Болотова Татьяна Владимировна
2.
Непременным условием развивающего обучения являетсяформирование у учеников умения рассуждать, то есть
делать умозаключение и уметь обосновывать
высказанное предположение. Дети начальных классов
должны научиться строить умозаключения по аналогии.
3.
Аналогия - особый вид умозаключений, когда по причинесходства двух объектов по некоторым признакам и при
наличии дополнительного признака у одного из них,
делается вывод о наличии такого же признака у другого
объекта.
Схематически:
Объект А обладает признаками а,b,с,х.
Объект В обладает признаками а,b,с.
Вывод: объект В обладает признаком Х
4.
Умозаключение по аналогии - это такое умозаключение,в котором на основании сходства двух объектов в некоторых
признаках и при наличии дополнительного признака у
одного из них, делается вывод о наличии такого же признака
у другого объекта.
5.
Выготский Л.С. отмечает, что природосообразныйхарактер детского мышления определяется, прежде всего,
преобладанием целостного эмоционально чувственного
познания мира — особой формы отражения
действительности посредством эмоциональных образов.
Эти особенности природосообразного характера детского
мышления подчеркивают значимость аналогии, в основе
которой — идея сходства между различными явлениями
действительности, способность к переносу известного в
малоизвестные явления. В мышлении ребенка аналогия
выступает «ключом к пониманию действительности,
всеобщим принципом объяснения мира», аналогия ставит
проблему, тогда как проверка, укрепление и устранение
суждения требуют новых процессов мышления.
6.
Прием аналогии в процессе обучения помогает ученикамоткрыть новые знания и способы деятельности, но, следует
иметь в виду, что вывод по аналогии является лишь
предположением, который в последующем необходимо
доказывать или опровергать. Эта особенность аналогии не
является препятствием для его использования в процессе
обучения математике, так как:
• рассуждения идут под руководством учителя, который может
поправить неверный вывод;
• учащиеся привыкают делать проверку полученного вывода.
7.
С целью ориентации учащихся на использование аналогиинеобходимо в доступной для них форме разъяснить её
сущность, обращая внимание на то, что в математике часто
открытие нового способа вычислений, правила,
закономерностей и т. п. осуществляется по догадке.
8.
Как отмечает профессор Пензенского ПГУ А.К. Артемов, дляприменения аналогии в начальном обучении, придерживаются
следующих правил:
1) аналогия основывается на сравнении и поэтому учащиеся
должны в достаточной степени владеть этим приемом;
2) для использования аналогии необходимо иметь два объекта,
один из которых хорошо известен учащимся, а другой сравнивается с
ним;
3) при сравнении объектов тщательно изучают их сходство и
различие в существенных в данной ситуации признаках;
4) при использовании аналогии учащимся в доступной форме
разъясняют цели его применения, обратив их внимание на то, что в
математике часто новые знания можно получить "по догадке",
внимательно изучая известное знание и данное задание.
9.
Вывод по аналогии осуществляется по следующим этапам:1)Выбираем 2 объекта, один из которых хорошо знаком
ученикам (известный), а другой пока мало изучен
(неизвестный). Эти объекты сравниваем по каким-либо
признакам и подчеркиваем их сходство;
2) Подмечаем, что известный объект обладает особым
свойством;
3) В силу сходства 2-х объектов делаем предположение о
том, что и неизвестный объект обладает этим же
свойством;
4) Выполняем проверку и убеждаемся, что предположение
было верным.
10.
В основе приема аналогии лежат:• анализ(операция, связанная с выделением
элементов данного объекта, его признаков и
свойств)
• синтез (соединение различных элементов в единое
целое);
• обобщение (мысленное объединение предметов и
явлений по их общим и существенным признакам);
• сравнение (сопоставление различных объектов,
нахождение их общих и различных признаков).
11.
В логике различает несколько видов аналогии, из которыхв начальном обучении математике учитель может
использовать:
• Аналогию свойств;
• Аналогию отношений;
• Аналогию действий.
12.
Аналогия свойствАналогия свойств- аналогия, при которой на основе изучения
существенных признаков одного объекта раскрываются новые
свойства изучаемого объекта.
Например, в качестве примера А.К. Артемов приводит следующий
факт: "Допустим, изучаются классы чисел. В классе единиц три разряда единицы, десятки, сотни. В классе тысяч также три разряда - единицы
тысяч, десятки тысяч, сотни тысяч. На вопросы "Сколько разрядов будет в
следующим классе, который называется классом миллионов?" и "Как они
называются?" учащиеся отвечают: "Три" - и называют их: "Единицы
миллионов, десятки миллионов, сотни миллионов". Это - вывод по
аналогии, в котором фиксируется определенное свойство вновь изучаемого
объекта (класса миллионов)"
13.
Аналогия отношенийАналогия отношений - аналогия, при которой между данными
объектами устанавливается некоторое отношение.
Т е м а: Сложение вида 34+20, 34+2 (1 класс).
Учащимся разъясняем цели применения аналогии: "Ребята! Сейчас мы
с вами решим один пример. Если правильно ответите на мои вопросы, то
вы сможете самостоятельно решить второй пример, который я напишу".
Разбираем решение примера 34+20=(30+4)+20=50+4=54 и выявляем
существенные признаки: представление числа в виде суммы разрядных
слагаемых, применение правила прибавления числа к сумме. После этого
предлагаем пример 34+2 и высказываем "догадку" - нельзя ли и здесь
поступить так же. Потом доказываем правомерность наших действий
решением 34+2= (30+4)+2=30+(4+2)=30+6=36 и проверкой по учебнику.
14.
Т е м а: Нахождение времени движения по известному расстоянию и скорости (3класс).
Перед решением задачи "Пассажир проехал в автобусе 90 км. Скорость автобуса 45
км/ч. Сколько времени ехал пассажир в автобусе? Запиши задачу в таблицу и реши её",
практически демонстрируя наши действия и беседуя с учащимися, последовательно
заполняем заранее приготовленную таблицу (последняя строка заполняется
учащимися из задачи самостоятельно):
Расстояние
Я прошагал
Ты прошагал
Пассажир
10 шагов
420 шагов
90 км
Скорость
2 шага в сек.
70 шагов в
мин.
45 км/ч
Время
10:2=5(с.)
420:70=6(мин
.)
90:45=2(часа)
Вывод: чтобы найти время движения надо расстояние разделить на скорость.
В этой аналогии, отношения, установленные в первых двух случаях, помогают
решить задачу и вывести соответствующее правило.
15.
З а д а ч а: "В школе юннатов было 128 кролика. Когда несколько кроликовподарили другой школе, у них осталось 92 кролика. Сколько кроликов подарили
юннаты?"
Допустим, что учащиеся по каким-то причинам (забыли, "страх" перед большими
числами и др.) затрудняются в решении задачи. Применяя аналогию, учитель
"возвращает" их в знакомую для них ранее ситуацию, сохраняя сюжет задачи. Как это
делается, видно из следующей записи:
Решаемая задача
Было - 128 кролика
Подарили - ?
Осталось - 92 кролика
Аналогичная задача
Было - 5 книг
Подарили - ?
Осталось - 3 книги
После устанавливаем, что новую задачу иногда легко решить, если вспомнить такую
же старую задачу с "маленькими" числами.
Как правило, аналогичная задача должна быть доступной для устного решения. В
обучении слабых учащихся большую роль играет именно такой вариант аналогии, т.к.
от условия данной задачи, через аналогичную задачу с "маленькими" числами с тем же
сюжетом, легко переходить к выбору необходимого для решения действия.
16.
Аналогия действийАналогия действий - аналогия, при которой на основе изучения ранее
известного объекта выводится способ действия с изучаемым объектом.
Т е м а: Вычитание вида 42-5 (1 класс).
Сначала повторим ранее изученную тему: решите пример 47+5 с подробным объяснением.
После решения 47+5=47+(3+2)=50+2=52 учитель проводит беседу:
- Почему к 47 сначала прибавили 3, а потом 2, можно ведь сначала прибавить 2, потом 3,
или же 1 и 4? (Прибавим 3 и 47 дополним до разрядного числа 50, а к нему прибавлять 2 уже
легче). Что самое главное при решении этого примера? (Главное - мы дополняем число до
разрядного.) Нельзя ли по этому свойству решить пример 42-5? (ответа может и не быть. А.А.). Хорошо. Мы в первом примере 47 дополнили до 50, а здесь какое у нас число? (Число
42). До какого разрядного числа его можно "довести" и как? (До 40, для этого нам надо вычесть
2) На доске пока запишем: 42-5=(42-2)... Но нам надо вычесть 5, а не 2. (Значит надо вычесть
еще и 3). Попытайтесь самостоятельно завершить пример. (42-5=(42-2)-3=40-3=37.) Правильно.
Ответьте теперь на вопрос: что же общего в этих примерах? ("Доводим" числа до разрядного
числа.) Какие правила при их решении использованы? (Прибавление сумму к числу и
вычитание суммы из числа). Ребята! А почему при изучении нового примера мы использовали
ранее нам известный? (Потому что тот мы уже знали. Потом новый пример сравнили с ним и
догадались: и здесь надо так делать.)
17.
Т е м а: Вычитание суммы из числа (1 класс).Под диктовку учащихся учитель на доске пишет три способа решения примера 7+(2+1):
7+(2+1)=7+3=10
7+(2+1)=(7+2)+1=9+1=10
7+(2+1)=(7+1)+2=8+2=10
Решение доказывают по правилу прибавления суммы к числу. После этого в примере
7+(2+1) во всех трех случаях впереди скобки "+" меняют на "-", получают пример
7-(2+1) и пытаются, заменив, где надо, "+" на "-", "исправить" решение. Полученные
способы решения:
7-(2+1)=7-3=4
7-(2+1)=(7-2)-1=5-1=4
7-(2+1)=(7-1)-2=6-2=4
проверяют по учебнику, доказывают их правильность по рисунку и выводят правило:
чтобы вычесть из числа сумму, можно из этого числа вычесть первое слагаемое и из
полученного числа вычесть второе слагаемое.
18.
Аналогия различается на:• простую аналогию, при которой по сходству объектов в
некоторых признаках заключают их сходство в других
признаках;
• распространенную аналогию, при которой из сходства
явлений делают вывод о сходстве причин.
19.
В свою очередь, простая и распространенная аналогияможет быть:
1) строгой аналогией, при которой признаки
сравниваемых объектов находятся во взаимной
зависимости;
2) нестрогой аналогией, при которой признаки
сравниваемых объектов не находятся в явной взаимной
зависимости
20.
Аналогия является одним из самыхраспространенных методов научного исследования.
Широкое применение аналогий часто приводит
исследователя к более или менее правдоподобным
предположениям о свойствах изучаемого объекта,
которые могут быть затем подтверждены или
опровергнуты опытом или более строгими
рассуждениями.
21.
Имеет смысл говорить о «полезной» и о «вредной»аналогии. Примером «полезной аналогии» является,
в частности, мысленный перенос многих понятий и
суждений, относящихся к планиметрии, в
геометрию трехмерного пространства.
22.
Например: «Прямоугольник аналогичен прямоугольномупараллелепипеду. В самом деле, отношения между
сторонами прямоугольника сходны с отношениями между
гранями параллелепипеда:
Каждая сторона прямоугольника параллельна и равна
одной другой стороне и перпендикулярна остальным.
Каждая грань прямоугольного параллелепипеда
параллельна и равна одной другой грани и
перпендикулярна остальным»
23.
Не менее явная аналогия существует и между площадьюпрямоугольника и объемом прямоугольного
параллелепипеда. Причем эта аналогия проявляется
весьма широко, начиная от сходства формул S = a b и V =
a b c и кончая сходством в структуре вывода этих
формул (распадающегося на случаи, когда измерения
названных фигур выражаются натуральными,
положительными рациональными и действительными
числами).
24.
В качестве примера «вредной аналогии» можно привести перенос известныхзаконов сложения конечных сумм на бесконечные.
Вот к каким результатам можно прийти, если, в частности, применить эту
аналогию при нахождении суммы ряда
S=1–1+1–1+1–1+…:
используя свойство прибавления разности, получим:
S = (1 –1) + (1 – 1)+(1 – 1)+ … = 0 + 0 + 0 … = 0
б) используя свойство вычитания разности, получим:
S = 1 – (1 – 1) – (1 – 1) – (1 – 1) = 1 – 0 – 0 – 0 – … = 1
в) используя сочетательное свойство для алгебраической суммы, имеем:
S = 1 – (1 – 1 + 1 – … ), или S = 1 – S, откуда 2S = 1 и S = ½
Понятно, что примененная здесь аналогия является незаконной; слишком
глубокое качественное различие между конечным и бесконечным в математике
уменьшает число аналогичных свойств, присущих тому и другому.
25.
Использование приема аналогии всовременных программах
начального обучения математики
26.
Использование аналогии при изученииарифметического материала
1. Табличные случаи умножения и деления, лежащие в основе умножения
и деления круглых чисел (с использованием знания разрядного состава
чисел):
а) умножение и деление чисел, оканчивающихся нулями (на основе
разрядного состава числа):
20 ∙ 3 = 2 д. ∙ 3 = 6д. = 60
80 : 4 = 8 д. : 4 = 2д. = 20
200 ∙ 3 = 2 с. ∙ 3 = 6 с. = 600
240 : 3 = 24 д. : 3 = 8д. = 80
б) умножение на круглое число (на основе разрядного состава числа и
сочетательного свойства умножения):
15 ∙ 30 = 15 ∙ (3 ∙ 10) = (15 ∙ 3) ∙ 10 = 45 ∙ 10 = 450
в) деление на круглые числа:
240 : 30 = 240: (10 ∙ 3) = 240 : 10 : 3 = 8
27.
2. Письменные приемы сложения, вычитания, умножения, деления начинают изучатьс простых случаев:
а) сложение
+ 73
+ 563
+ 826
+ 6123
+ 4028
65
97
739
879
3796
б) вычитание
в) умножение
x 32
x 36
9
22
г) деление
x
374
2
x
374
92
x5023
4
x
11099
2
28.
3. Свойство прибавления числа к сумме, усвоенное для случаев:34 + 20 = (30 + 4) + 20 = (30 + 20) + 4 = 50 + 4 = 54,
34 + 5 = (30 + 4) + 5 = 30 + (4 + 5) = 30 + 9 + 39,
может быть использовано при вычислениях вида:
37 + 25 = (30 + 7) + (20 + 5) + (30 + 20) + (7 +5) = 50 + 12 = 62
29.
4. Умножение и деление многозначного числа на однозначноевыполняется по аналогии с умножением (делением) двузначного
числа на однозначное (на основе разрядного состава числа и
распределительного закона умножения (деления) относительно
сложения):
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
69 : 3 = (60 + 9) : 3 = 60 : 3 + 9 : 3 = 20 + 3 = 23
418 ∙ 3 = (400 + 10 + 8) ∙ 3 = 400 ∙ 3 + 10 ∙ 3 + 8 ∙ 3 = 1200 + 30 + 24
= 1254
8408 : 4 = (8 000 + 400 + 8) : 4 = 8000: 4 + 400 : 4 + 8 : 4 = 2000 +
100 + 2 = 2102
30.
5. Умножение многозначных чисел опирается на умножениемногозначного числа на однозначное (на основе разрядного
состава числа и распределительного закона умножения
относительно сложения):
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192;
286 ∙ 374 = 286 ∙ 300 + 286 ∙ 70 + 286 ∙ 4
Здесь можно ограничиться планом решения, так как это
подготовка к письменным приёмам умножения.
31.
Использование аналогии при изучениигеометрического материала
1. «Квадрат» по аналогии с «Прямоугольник»
Сравниваем две фигуры и обсуждаем то, что раз квадрат
тоже четырехугольник, у которого все углы прямые, то он
тоже прямоугольник и его периметр можно найти также.
32.
2. Прямоугольник аналогичен прямоугольному параллелепипеду.Отношения между сторонами прямоугольника сходны с
отношениями между гранями параллелепипеда:
- Каждая сторона прямоугольника параллельна и равна одной
другой стороне и перпендикулярна остальным.
- Каждая грань прямоугольного параллелепипеда параллельна и
равна одной другой грани и перпендикулярна остальным.
33.
3. Сравни треугольники. Чем они похожи?– Каждый из этих треугольников называют прямоугольными.
Подумай, почему им дали такое название.
– Попробуй дать определение прямоугольного треугольника.
– Сравни своё определение с таким:
Треугольник, у которого есть прямой угол, называется
прямоугольным.
Определения похожи? Если не похожи, то чем?
– Начерти разные прямоугольные треугольники.
34.
4. Сравни треугольники– Выпиши номера треугольников, название которых мы
изучили
– Придумай названия остальным треугольникам.
– Подумай, им подойдёт название тупоугольные? Предложи
своё определение тупоугольного треугольника.
– Если ты затрудняешься, вернись к определению
прямоугольного треугольника. Чем будет отличаться новое
определение?
– Начерти разные тупоугольные треугольники.
35.
Использование аналогии при решениизадач
Для использования аналогии в процессе обучение решению
задач необходимо вначале восстановить способ решение
аналогичной задачи. Затем предлагать решить новую задачу.
Учащиеся путем сравнения выявляют сходство отношений
новой задачи с отношениями в ранее решенной задачи. На
основе установление сходства, они делают вывод, что план
решение новой задачи похожим на план ранее решенной
задачи.
36.
Рассмотрим пример использования аналогии при решениизадач отличающихся друг от друга содержанием, но имеющих
сходство в отношениях между данными.
Задача 1. Из двух городов, находящихся на расстоянии 420 км
друг от друга, выехали одновременно навстречу друг другу
мотоциклист со скоростью 60 км/ч и автомобилист со
скоростью 80 км/ч. Через сколько часов они встретятся?
Задача 2. Мастер за час изготавливает 80 деталей, а ученик –
60 деталей. За сколько часов, работая вместе, они изготовят
420 деталей?
37.
Осуществляя сравнение задачи № 2 с ранее решеннойзадачей № 1 учитель обращает внимание учащихся на
сходство отношений данных в этих задачах:
• Количество деталей – расстояние;
• Время совместной работы – время совместного
движения;
• Производительность труда каждого мастера – скорость
каждого предмета.
38.
Задачу 1 решали путем нахождения общей скорости движениямотоциклиста и автомобилиста и деления на нее данной длины
пути. У учащихся возникает догадка, что данную задачу нужно
решать аналогично, но только сначала нужно найти
производительность в час мастера и ученика (то есть отвечают
на вопрос: сколько деталей изготавливает мастер и ученик за 1
час?).
Получим: 1) 80+60=140 (дет) – изготовят мастер и ученик за 1
час. 2) 420: 140=3(ч) – число дней совместной работы.
Проверка позволяет установить правильность решения задачи:
80×3+60×3=420 (деталей).
39.
Примеры умозаключений по аналогии,которые можно использовать при изучении
математических понятий в 1 – 4 классах в
виде фрагментов уроков
40.
1 классСложение и вычитание вида
+ 4,
-4
Выбираем 2 объекта. На доске записи:
6+3
6+4
9-3
10 - 4
Сравниваем эти записи: перечисляем общие признаки и
отличия.
Сходства: одинаковые знаки действия в каждой строке, в
каждом столбике действия выполняются с одним и тем же
числом;
Отличия: числа в столбиках.
41.
2) Подмечаем, что известный объект обладает особымсвойством:
Вспоминаем, что не так давно, в предыдущей части
учебника, изучали прием
3- это 2 да 1. Чтобы к числу прибавить 3, нужно три
раза прибавить по 1 или прибавить 2, а затем прибавить
1. Чтобы из числа вычесть 3, нужно три раза вычесть 1
или вычесть 2, а затем вычесть 1.
42.
3)Делаем предположение, что приемже образом.
решается таким
Предположение:
4- это 2 да 2. Чтобы к числу прибавить 4, нужно два раза
прибавить по 2 или прибавить 3, а затем прибавить 1.
Чтобы из числа вычесть 4, нужно два раза вычесть по 2
или вычесть 3, а затем вычесть 1.
6+4=6+2+2=6+3+1=9
10 – 4 = 10 – 2 – 2 = 10 – 3 – 1 = 1
43.
4)Так как мы это предположили, то вывод может быть и неверным. Поэтому необходимо выполнить проверку.
Для этого на доску выводим числовой ряд
44.
Сначала проверяем сложение. Для этого, от цифры 5 двигаемсявправо на четыре шага. На какое число мы попали? (мы попали
на число 9). Какой вывод из этого мы можем сделать? (наше
предположение оказалось верным).
Проверим вычитание. Для этого, от цифры 10 двигаемся влево
на четыре шага. На какое число мы попали? (мы попали на
число 6). Какой вывод из этого мы можем сделать? (наше
предположение оказалось верным).
45.
2 классПрием вычисления вида 35-7
1) Выбираем 2 объекта. На доске 2 выражения
35 + 7
35 – 7
Сравниваем эти выражения: перечисляем общие признаки и
отличия.
Сходства: одинаковые числа
Отличия: разные действия
Подмечаем, что известный объект обладает особым
свойством:
46.
2) Подмечаем, что известный объект обладает особымсвойством:
Вспоминаем, что на предыдущем уроке мы научились
выполнять подобные действия со сложением.
26 это 2 десятка и 6 единиц. Чтобы к числу 26 прибавить 7,
надо сначала 26 довести до круглого десятка, возьмем 4
единицы у второго слагаемого, второе слагаемое 7 – это 4 и 3.
К 26 прибавим 4, получили круглое число 30. Далее к 30
прибавляем 3. Получаем число 33.
47.
3) Делаем предположение, что и в том, и в другомвыражении действия выполняются через разряд десятков.
Значит, видимо, можно вычесть тем же способом, что и в
сложении, т. е. довести число до десятка, а потом вычесть
оставшуюся часть.
Предположение: 35 это 3 десятка и 5 единиц. Чтобы
из числа 35 вычесть 7, надо сначала число 35 довести до
круглого десятка, вычтем 5 единиц у второго слагаемого,
второе слагаемое 7 – это5 и 2. Из 35 вычитаем 5,
получили круглое число 30. Далее из 30 вычитаем 2.
Получаем число 28.
48.
4) Так как мы это предположили, то вывод может быть и неверным. Поэтому необходимо выполнить проверку.
Для этого число 35 выложим с помощью палочек.
Возьмем три пучка по 10 штук и 5 палочек отдельно.
Почему? (потому что число 35 – это 3 десятка и 5 единиц.)
49.
50.
Уберем из этого числа 7 палочек, что получиться?(убираем 5 палочек, так как нам нужно убрать 7, то еще
две палочки убираем из пучка, следовательно получается 2
пучка и 8 палочек). Какое число получилось и почему?
(Число 28 – потому что 2 десятка (пучка) и 8 единиц).
Какой вывод из этого мы можем сделать? (наше
предположение оказалось верным).
51.
3 классСложение трехзначных чисел в столбик
1)Выбираем 2 объекта. На доске 2 выражения
Сравниваем эти выражения: перечисляем общие признаки
и отличия.
Сходства: одинаковые знаки действия;
Отличия: в первом выражении складываются двузначные
числа, а во втором трехзначные.
52.
2) Подмечаем, что известный объект обладает особымсвойством:
Вспоминаем, что во 2 классе мы знакомились с письменным
приемом сложения столбиком.
Вспоминаем алгоритм письменного сложения в пределах 100:
1.Пишу десятки под десятками, а единицы под единицами.
2.Складываю единицы, пишу под единицами.
3.Складываю десятки, пишу под десятками.
4.Читаю ответ.
53.
3)Делаем предположение, что и трехзначные числа можноскладывать также, но появляется новый шаг - сложение
сотен.
4) Для проверки можно использовать модель (абак)
54.
СотниДесятки
Единицы
Можно для проверки подсчитать, используя устный прием в
строчку: 523+142=523+(100+40+2)=665
55.
4 классПисьменное деление многозначного числа на однозначное
число.
1)Выбираем 2 объекта. На доске 2 выражения
986:2
8876:7
Сравниваем эти выражения: перечисляем общие признаки и
отличия.
Сходства: одинаковые знаки действия, деление на однозначное
число;
Отличия: в первом выражении делят трехзначное число, а во
втором четырехзначное.
56.
2)Подмечаем, что известный объект обладает особым свойством:Вспоминаем, что мы уже изучали деление трехзначного числа на однозначное
Вспоминаем алгоритм деления трехзначного числа на однозначное:
1. Делим сотни
2. Умножаем полученное число на делитель
3. Вычитаем из сотен полученное произведение
4. Переносим десятки
5. Делим десятки
6. Умножаем полученное число на делитель
7. Вычитаем из десятков полученное произведение
8. Переносим единицы
9. Делим единицы
10. Умножаем полученное число на делитель
11. Вычитаем из единиц полученное произведение
12. Пишем нуль
57.
3)Делаем предположение, что и многозначные числа можноскладывать также, только еще появляется разряд тысяч.
58.
4)Так как мы это предположили, то вывод может быть и неверным. Поэтому необходимо выполнить проверку.
Для этого проверим результат деления умножением.
59.
Примеры некоторых понятий, изучаемых вначальном курсе математики, дополнительные
сведения о которых можно использовать на
уроках в начальной школе
60.
Значение понятия вматематике
Квадрат –
1) прямоугольник с равными
сторонами. 2) вторая степень
числа (а), то есть а2
Значение понятия в
Перевод с греческого,
других областях
латинского
Квадрат – в полиграфии От лат. – quadratus
единица
длины, − четырехугольный
применяемая
для
измерения шрифтов,
формата
набора.
1
квадрат = 48 пунктам (ок.
18,05 мм).
Круг - часть плоскости, Круг – в древности, От лат. «кольцо»
ограниченная окружностью повязка на плече как
(содержащая ее центр). знак отличия
Площадь круга S = R , где R радиус
окружности,
а
=
3,141592654…
отношение
длины
окружности к диаметру.
Линия - общая часть двух Линия 1) единица от лат. linea – льняная
смежных
областей длины
в
системе нить
поверхности.
Движущаяся английских мер, 1 линия
точка описывает при своем = 1/12 дюйма =0,21167
движении некоторую линию. см. 2) В России - мера
Прямая линия – черта или длины, 1 линия = 10
прямая
точкам =2,54 мм.
61.
Значение понятия вматематике
Значение понятия в
других областях
Перевод с греческого,
латинского
Периметр - длина
замкнутого контура,
сумма длин всех сторон
многоугольника
Периметр - в
математике: граница
плоской фигуры, а также
длина этой границы.
от греч . perimetreo измеряю вокруг греч.
perimetron - окружность
Ромб – параллелограмм
с равными сторонами
Ромб - Название
высшего офицерского
знака различия такой
формы на петлицах в
Красной Армии
греч . rhombos
Треугольник геометрическая фигура многоугольник с тремя
углами.
Часть плоскости,
ограниченная тремя
отрезками прямых
(сторонами
треугольника),
имеющими попарно по
одному общему концу
Треугольник - Созвездие лат . Triangulum
Северного полушария; с
территории России
лучше всего видно в
конце лета, осенью и
зимой.
62.
Значение понятия вматематике
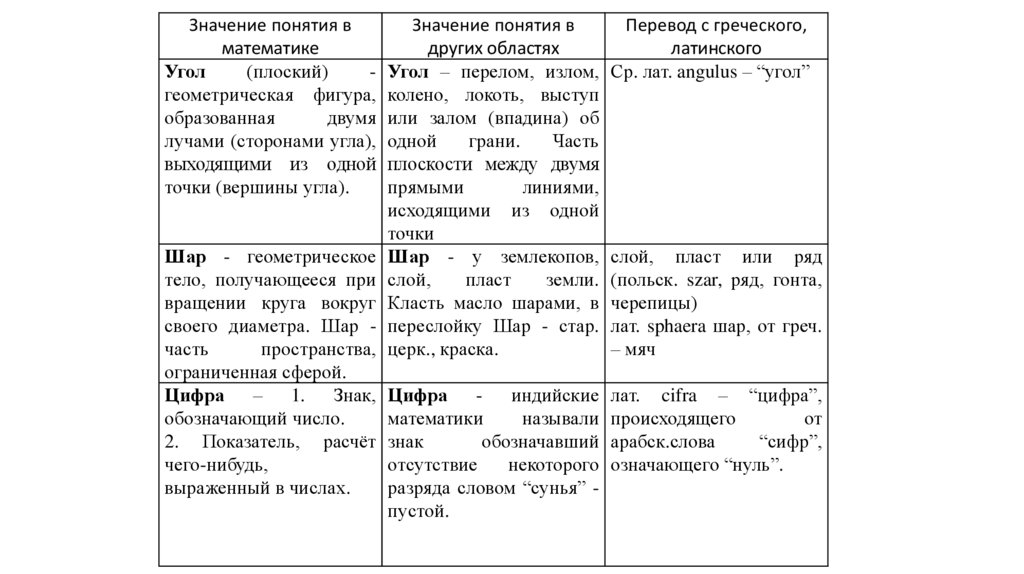
Угол
(плоский)
геометрическая фигура,
образованная
двумя
лучами (сторонами угла),
выходящими из одной
точки (вершины угла).
Шар - геометрическое
тело, получающееся при
вращении круга вокруг
своего диаметра. Шар часть
пространства,
ограниченная сферой.
Цифра – 1. Знак,
обозначающий число.
2. Показатель, расчёт
чего-нибудь,
выраженный в числах.
Значение понятия в
других областях
Угол – перелом, излом,
колено, локоть, выступ
или залом (впадина) об
одной
грани.
Часть
плоскости между двумя
прямыми
линиями,
исходящими из одной
точки
Шар - у землекопов,
слой,
пласт
земли.
Класть масло шарами, в
переслойку Шар - стар.
церк., краска.
Перевод с греческого,
латинского
Ср. лат. angulus – “угол”
Цифра - индийские
математики
называли
знак
обозначавший
отсутствие
некоторого
разряда словом “сунья” пустой.
лат. cifra – “цифра”,
происходящего
от
арабск.слова
“сифр”,
означающего “нуль”.
слой, пласт или ряд
(польск. szar, ряд, гонта,
черепицы)
лат. sphaera шар, от греч.
– мяч
63.
Значение понятия вматематике
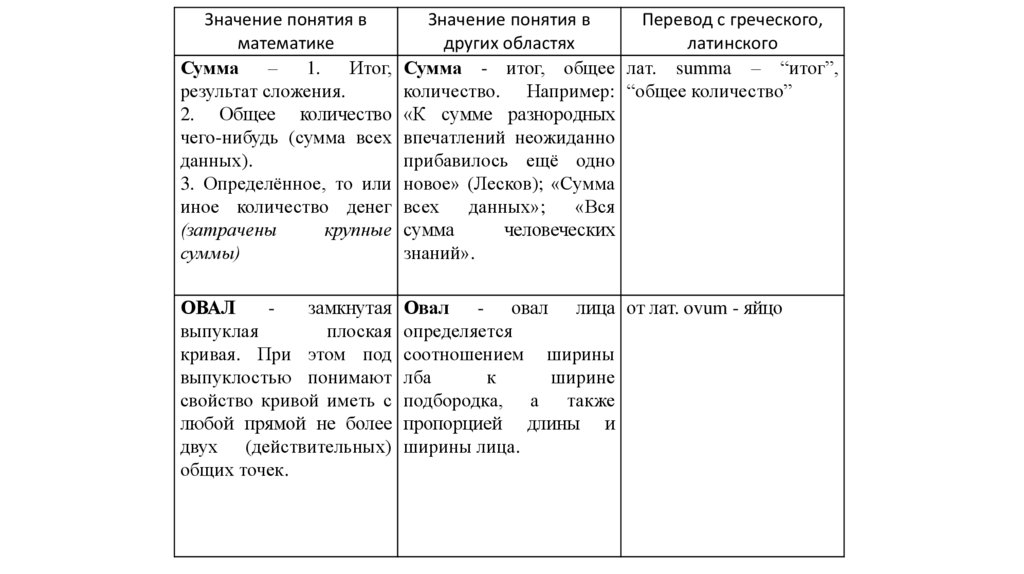
Сумма
– 1.
Итог,
результат сложения.
2. Общее количество
чего-нибудь (сумма всех
данных).
3. Определённое, то или
иное количество денег
(затрачены
крупные
суммы)
Значение понятия в
Перевод с греческого,
других областях
латинского
Сумма - итог, общее лат. summa – “итог”,
количество. Например: “общее количество”
«К сумме разнородных
впечатлений неожиданно
прибавилось ещё одно
новое» (Лесков); «Сумма
всех
данных»;
«Вся
сумма
человеческих
знаний».
ОВАЛ
замкнутая
выпуклая
плоская
кривая. При этом под
выпуклостью понимают
свойство кривой иметь с
любой прямой не более
двух (действительных)
общих точек.
Овал - овал лица от лат. ovum - яйцо
определяется
соотношением ширины
лба
к
ширине
подбородка, а также
пропорцией длины и
ширины лица.
64.
Значение понятия вматематике
Площадь
–
1.
В
математике:
часть
плоскости, заключённой
внутри
замкнутой
геометрической фигуры
(площади квадрата).
2.
Незастроенное
большое ровное место (в
городе, в селе), от
которого
обычно
расходятся в разные
стороны улицы (Красная
площадь в Москве).
3.
Пространство.
Помещение,
предназначенное
для
какой-нибудь
цели
(полезная площадь в
доме).
Значение понятия в
Перевод с греческого,
других областях
латинского
Площадь
часть греч.
plateia
–
поверхности,
“широкая”.
ограниченная
какимлибо
замкнутым
контуром. Величина П.
выражается
числом
заключающихся в ней
квадратных единиц.
65.
Значение понятия вматематике
Куб – 1. Правильный
шестигранник, все грани
которого – квадраты.
2.
В
математике:
произведение
от
умножения
данного
числа на само себя
дважды.
3. Кубический метр как
мера объёма.
4. Сосуд для перегонки и
кипячения жидкостей.
Значение понятия в
Перевод с греческого,
других областях
латинского
Куб
кубоватый, греч. kubos – “игральная
кубастый, кубовидный, - кость”.
образный,
почти
кубичный, близкий к
кубу
по
виду,
сундуковатый. а³
Сфера – 1. Область,
пределы
распространения
чегонибудь.
2. Среда, общественное
окружение.
Сфера
—
сфера греч. sfaira
экономики,
где “мяч”.
производятся
блага,
полезный
эффект
которых проявляется в
самом
процессе
их
создания.
–
“шар”,
66.
Значение понятия вматематике
Цилиндр
–
1.
В
математике:
геометрическое
тело,
образуемое вращением
прямоугольника вокруг
одной из его сторон.
2. Предмет такой формы
(напр., часть в машине).
3.
Высокая
твёрдая
шляпа такой формы с
небольшими полями.
Значение понятия в
Перевод с греческого,
других областях
латинского
Цилиндром
- греч. kilindros – “валик”,
называется тело, которое “каток”
состоит из двух кругов,
совмещаемых
параллельным
переносом,
и
всех
отрезков, соединяющих
соответствующие точки
этих кругов
67.
Для того, чтобы детям было интереснее изучать предмет,им можно предложить изучение материала в виде игры.
Вот один из вариантов:
Подготавливаются карточки двух видов. На одних
карточках написаны математические термины. Например:
овал, круг, цилиндр, угол, шар, куб, площадь.
На других – перевод этих слов с латинского или
греческого языков с изображением соответствующего
объекта.
Например:
68.
69.
На обратной стороне этих карточек можно написать историюпроисхождения и развития этих терминов, интересные сведения
из опыта их использования. Это позволит повысить интерес,
расширить кругозор детей, повысить мотивацию учения.
Таким образом, прием аналогии можно использовать при
изучении различных математических понятий, законов,
формировании общеучебных умений.
70.
Примеры типичных ошибок в вычислениях,которые допускают учащиеся начальных
классов при необоснованном использовании
приема аналогии
71.
Неверный результат получается иногда вследствиеиспользования нерациональных приемов.
Например, выполняя сложение в случаях вида 3 + 6, часть учеников вместо
приема перестановки слагаемых использует прием присчитывания по
единице (по 2, по 3), а это трудно, и ученики часто забывают, сколько единиц
они уже прибавили и сколько осталось прибавить, вследствие чего получают
неправильный результат (3 + 6 = 8, 3 + 6 = 10 и т. п.).
Предупреждению таких ошибок помогает сравнение рациональных и
нерациональных приемов вычислений. Так, обнаружив, что некоторые
ученики допускают ошибки при решении примеров вида 3 + 6, учитель
спрашивает, как они решали пример (3 + 1 = 4, 4 + 1 = 5 и т. д.), затем другие
ученики объясняют, как можно решить этот пример быстрее, легче (надо
переставить слагаемые 6 + 3 = 9, результат помним наизусть). Здесь же
ученики указывают, в каких случаях следует переставлять слагаемые (когда к
меньшему числу прибавляем большее).
72.
Смешение приемов вычитания, основанных насвойствах вычитания суммы из числа и числа из суммы.
Например:
50 – 36 = 50 – (30 + 6) = (50 – 30) + 6 = 26
56 – 30 = (50 + 6) – 30 = (50 – 30) – 6 = 14
Чтобы предупредить появление подобных ошибок, надо проводить специальную работу по
сравнению смешиваемых приемов, выявляя при этом существенное различие. Ученикам
предлагаются пары примеров, аналогичные приведенным, решая которые, они сравнивают каждый
следующий шаг:
80 – 27 = 80 – (20 + 7)
87 – 20 = (80 + 7) – 20
В первом примере надо вычитать из 80 сумму чисел 20 и 7, а во втором – вычитать одно число 20
из суммы чисел 80 и 7.
80 – 27 = 80 – (20 + 7) = (80 – 20) – 7 = 53
87 – 20 = (80 + 7) – 20 = (80 – 20) + 7 = 67
В первом примере вычли 20 и вычли 7, а во втором вычли только 20 из 80 и к результату прибавили
7.
Целесообразно провести также сравнение приемов для случаев вида 60 – 28 и 68 – 20, 14 – 6 и 16 –
4 и т. п.
73.
Выполнение сложения и вычитания над числамиразных разрядов как над числами одного разряда.
Например, ученик складывает число десятков с числом единиц 54 + 2 = 74,
вычитает из числа единиц число десятков 57 – 40 = 53 и т. п.
Для предупреждения названных ошибок полезно обсудить неверные
решения примеров. Так, учитель предлагает найти среди данных примеров
те, при решении которых допущена ошибка: 42 + 3 = 45; 25 + 4 = 65; 54 +
30 = 57. Затем выясняется, какая допущена ошибка: во втором примере 4
единицы прибавили к двум десяткам и получили шесть десятков, это
неправильно, единицы надо прибавлять к единицам, получится 29, а не 65;
в третьем примере 3 десятка прибавили к четырем единицам получили
семь единиц, это неверно, десятки надо прибавлять к десяткам, получится
84, а не 57. После этого еще раз повторяется, что единицы прибавляют к
единицам, а десятки к десяткам. Такую работу следует провести и при
рассмотрении примеров на вычитание. С учениками, которые часто
допускают подобные ошибки, полезно вернуться к использованию
счетного материала (пучки палочек и отдельные палочки, полоски с
кружками и другие).
74.
Смешение приемов внетабличного умножения иделения с приемом сложения.
Например: 35 * 2 = 65, 68 : 2 = 38.
Чтобы предупредить, а позднее устранить подобные ошибки, следует
предлагать для решения с подробной записью и объяснением пары
примеров вида 16 * 4 и 16 + 4, попутно выявляя существенное различие
в приемах: при умножении двузначного числа на однозначное умножают
на него и десятки, и единицы, после чего результаты складывают, а при
сложении прибавляют однозначное число только к единицам. Такое же
сравнение ведется при решении пар примеров вида 36 : 3 и 36 + 3. Для
устранения подобных ошибок полезно проводить обсуждение неверных
решений, аналогичных приведенным, в результате которого ученики
сами находят ошибку (единицы не умножили или не разделили на число
2). Важно также, чтобы ученики выполняли проверку решения примеров
на внетабличное умножение и деление: умножение проверяли делением
произведения на один из компонентов, а деление – либо умножением
частного на делитель, либо делением делимого на частное. Проверку
следует выполнять преимущественно устно.
75.
Смешение приемов внетабличного деления.Например: 88 : 22 = 44, 36 : 12 = 33.
Здесь ученики вместо использования приема подбора частного,
как и при делении двузначного числа на однозначное, делят
десятки, получая при этом десятки, затем делят единицы и
результаты складывают.
Для предупреждения таких ошибок целесообразно предложить
для решения одновременно примеры вида 88 : 22 и 88 : 2, после
чего сравнить как сами примеры, так и приемы их вычислений. В
таких случаях также полезно проводить обсуждение неверно
решенных примеров, выявляя при этом ошибку.
76.
Ошибки, вызванные смешением устных приемов умноженияна двузначные разрядные и неразрядные числа.
Например: 34 * 20 = 408 (умножили 34 на 2, затем 34 умножили на 10 и
сложили полученные произведения 58 и 340), 34 * 12 = 680 (умножили 34
на 2 и результат 68 умножили на 10).
Как и в других случаях смешения приемов, целесообразно сравнить их и
установить существенное различие: при умножении на разрядные числа
умножаем число на произведение, т.е. умножаем его на один из
множителей, а при умножении на двузначные неразрядные числа
умножаем число на сумму разрядных слагаемых: умножаем его на каждое
слагаемое и результаты складываем. Умение выполнять проверку решения
способом прикидки результата и, опираясь на связь между компонентами
и результатом умножения, поможет ученикам выявить ошибку.
77.
Ошибки, обусловленные смешением устных приемовделения на разрядные числа и умножения на
двузначные неразрядные числа.
Например: 420 : 70 = 102.
Ученик по аналогии с умножением на двузначное неразрядное число выполнил
деление так: разделили 420 на 10, затем 420 разделили на 7 и полученные
результаты 42 и 60 сложили.
Для предупреждения таких ошибок надо сравнить приемы для соответствующих
случаев деления и умножения (420 : 70 и 42 * 17) и установить существенное
различие (при делении на разрядные двузначные числа – делим на произведение,
а при умножении на двузначные неразрядные числа – умножаем на сумму).
Полезно с этой же целью проанализировать решения, в которых допущены
ошибки, аналогичные приведенным. Такие ошибки легко могут установить сами
ученики, если выполнят проверку, умножив частное на делитель (102 * 7 = 7140,
а должно получиться 420).
78.
С целью формирования у младших школьников приемааналогии можно предложить следующие задания:
– предлагать образец и требовать выполнения задания в
точности по образцу;
– предлагать задания, в котором даётся образец и требуется
выполнить задание по аналогии с образцом, но в измененных
условиях;
– предлагать задания, не требующие вычислений;
– составлять задачу, аналогичную данной;
– проводить рассуждение при решении задачи по аналогии с
решением сходной задачи.
79.
Анализ вариативных программ в курсематематики начальных классов
80.
Программа Моро М. И.(УМК «Школа России»)
81.
М1М ч.1, с.27- учащиеся по аналогии с имеющимисярисунками определяют, что можно сделать, чтобы всех
игрушек стало поровну
82.
В данных заданиях учащиеся определяют закономерность,по которой составлена таблица, и рисуют в свободной
клетке нужную фигуру по аналогии
М1М ч.1, с.27
М1М ч.1, с.29
М1М ч.1, с.75
83.
Учащиеся в тетрадях чертят фигуру, которая аналогичнатой, что дана на полях страницы
М1М ч.1, с.51
М1М ч.1, с.56
84.
М1М ч.1, с.73- учащиеся смотрят на первые вычисления ипродолжают их по аналогии
85.
Учащиеся сравнивают примеры в каждом столбике, определятзакономерность и по аналогии записывают следующий пример
М1М ч.1, с.101
М2М ч.1, с.28
86.
Учащиеся по аналогии с первым столбиком вписывают впустые окошки нужные числа/знаки
М1М ч.1, с.112
М2М ч.1, с.34
87.
Учащиеся находят закономерность написания следующихчисел в ряду и продолжают по аналогии
М1М ч.2, с.25
М3М ч.1, с.39
М4М ч.1, с.34
М2М ч.2, с.13
88.
Учащиеся по аналогии с первым столбцом таблицывыполняют заполнение всей таблицы
М1М ч.2, с.37
М4М ч.1, с.29
М2М ч.1, с.78
89.
М1М ч.2, с.59- учащиеся находят закономерностьполучения каждого числа нижнего ряда из числа,
записанного над ним в верхнем ряду и продолжают
нижний ряд по аналогии
90.
Учащиеся по аналогии с примером выполняют заданиеМ1М ч.2, с.102
М3М ч.1, с.28
91.
М2М ч.1, с.29- учащиеся находят закономерностьнаписания двузначных чисел и по аналогии продолжают
запись
92.
Учащиеся по аналогии с задачами составляют свою задачуМ2М ч.1, с.55
М3М ч.1, с.73
М4М ч.2, с.33
93.
Программа Чекина А. Л.(УМК «Перспективная начальная школа»)
94.
М1Ч ч.1, с.33- учащиеся по аналогии с рисунком, которыйдан на странице учебника, рисуют его в тетради
95.
М2Ч ч.1, с.68- учащиеся устанавливают правило, покоторому составлена последовательность и по аналогии
составляют свою последовательность
96.
М3Ч ч.1, с.22- учащиеся по аналогии выполняютпостроение в тетради
97.
М3Ч ч.2, с.15- учащиеся по аналогии составляютравенство для выражения
98.
М3Ч ч.2, с.22-23- учащиеся по аналогии вычисляютзначение произведения
99.
М4Ч ч.1, с.60- учащиеся приведен соответствующийслучай деления с остатком и для следующего равенства
аналогично они составляют и записывают другой случай
деления с остатком
100.
М4Ч ч.1, с.86- учащиеся должны ответить на вопрос отом, какая величина аналогична величине «скорость»
101.
Учащиеся устанавливают закономерностьпоследовательности чисел и по аналогии продолжают ряд
М3Ч ч.2, с.135
М4Ч ч.1, с.113
102.
Программа Истоминой Н. Б.(УМК «Гармония»)
103.
Учащиеся устанавливают закономерность составленныхстолбцов и по аналогии продолжают каждый из них.
М1И ч.1, с.78
М2И ч.1, с.68
104.
М2И ч.1, с.4- учащиеся находят правило, по которомусоставлена таблица и по аналогии записывают верные
равенства по тому же правилу
105.
М2И ч.1, с.4- учащиеся находят правило, по которомусоставлены пары выражений и по аналогии составляют
пары выражений только уже с другими числами
106.
М2И ч.1, с.31- учащиеся догадываются, что обозначено втаблице знаками + и –, и по аналогии завершают ее
заполнение
107.
М2И ч.1, с.77- учащиеся разгадывают правила, покоторому подобраны 3 числа и по аналогии с ними
записывают верные равенства
108.
Учащиеся находят закономерность написания ряда чисел ипо аналогии продолжают его
М4И ч.1, с.4
М3И ч.1, с.4
М2И ч.2, с.17
109.
Учащиеся устанавливаю правило, по которому составленыстолбцы выражений и по аналогии составляют такие же
столбцы для других выражений
М4И ч.1, с.3
М2И ч.1, с.68
110.
Программа Демидовой Т. Е.(УМК «Школа 2100»)
111.
Учащиеся по аналогии с фигурами, которые даны вучебнике рисуют фигуры в тетради
М1Д ч.2, с.5
М2Д ч.1, с.41
112.
Учащиеся находят закономерность и по аналогиипродолжают ряд чисел
М2Д ч.1, с.41
М3Д ч.1, с.36
М4Д ч.2, с.65
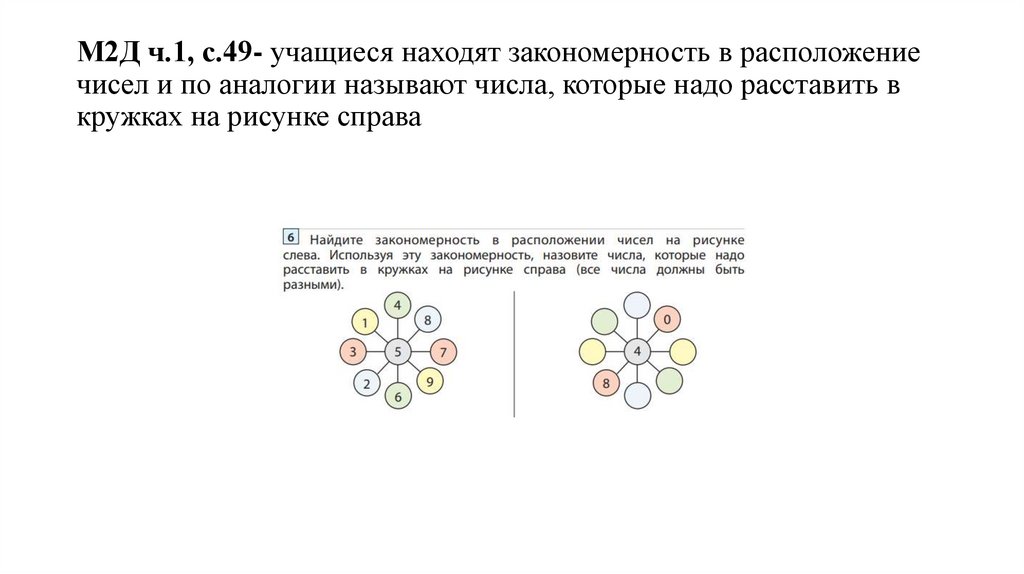
113.
М2Д ч.1, с.49- учащиеся находят закономерность в расположениечисел и по аналогии называют числа, которые надо расставить в
кружках на рисунке справа
114.
М2Д ч.1, с.73- учащиеся по аналогии с даннымипредметами в таблице определяют какие из предметов на
рисунке справа можно поместить в таблицу
115.
М4Д ч.1, с.45- учащиеся находят закономерность и поаналогии продолжают записи каждого столбика хотя бы на
одно выражение
116.
М4Д ч.2, с.23- учащиеся по аналогии срисунками, которые даны в учебнике рисуют
их в тетради
117.
ВыводПроанализировав вариативные программы мы можем прийти к
выводу о том, что в каждой из них прием аналогии используется
крайне редко, зачастую это однотипные задания, которые переходят
из класса в класс. В таком случае учитель должен сам
придумывать различные способы использования аналогии на
уроке, так как в начальном курсе математики она имеет большое
значение. Обнаружение сходства или различия между предметами
поднимает мышление на более высокую степень. Учащийся учится
умению делать предположения, умению познавать неизвестное,
овладевает навыками логического исследования предметов и
явлений окружающей действительности.


















































































































 Математика
Математика Педагогика
Педагогика








