Математика в архитектуре

1.

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
ПО ТЕМЕ : «МАТЕМАТИКА В
АРХИТЕКТУРЕ»
Студента группы:
АРХ-201
Даниил Парахин
Владимирович
Специальность:
Архитектура
Руководитель: Рыбина
Татьяна Викторовна
Дисциплина: Математика
Ставрополь, 2021

2.

Содержание
Введение.
Основное содержание:
• 1) Понятия – математика и архитектура
• 2) Как математика помогает добиться прочности
сооружений
• 3) Геометрические формы в разных архитектурных
стилях
• 4) Симметрия – царица архитектурного совершенства
• 5) Золотое сечение в архитектуре
Заключение.
Список источников информации.
Приложения.

3.

Введение
Сложно представить современное градостроительство без
математических знаний. Ведь сейчас при строительстве
используются новые технологии, появляются здания необычных,
сложных форм.
Цель: проанализировать взаимосвязь математики и архитектуры и
выяснить, как она проявляется в постройках разных культур и, в
частности, в зданиях города Новосибирска.
Задачи:
• 1) Изучить понятие архитектура и математика.
• 2) Выявить влияние математики на архитектуру.
• 3) Изучить математические понятия: симметрия, асимметрия,
диссимметрия, золотое сечение и их применение в архитектуре.
• 4) Исследовать архитектуру г. Новосибирска и рассмотреть
применение математических закономерностей и
геометрических форм.

4.

Основное
содержание
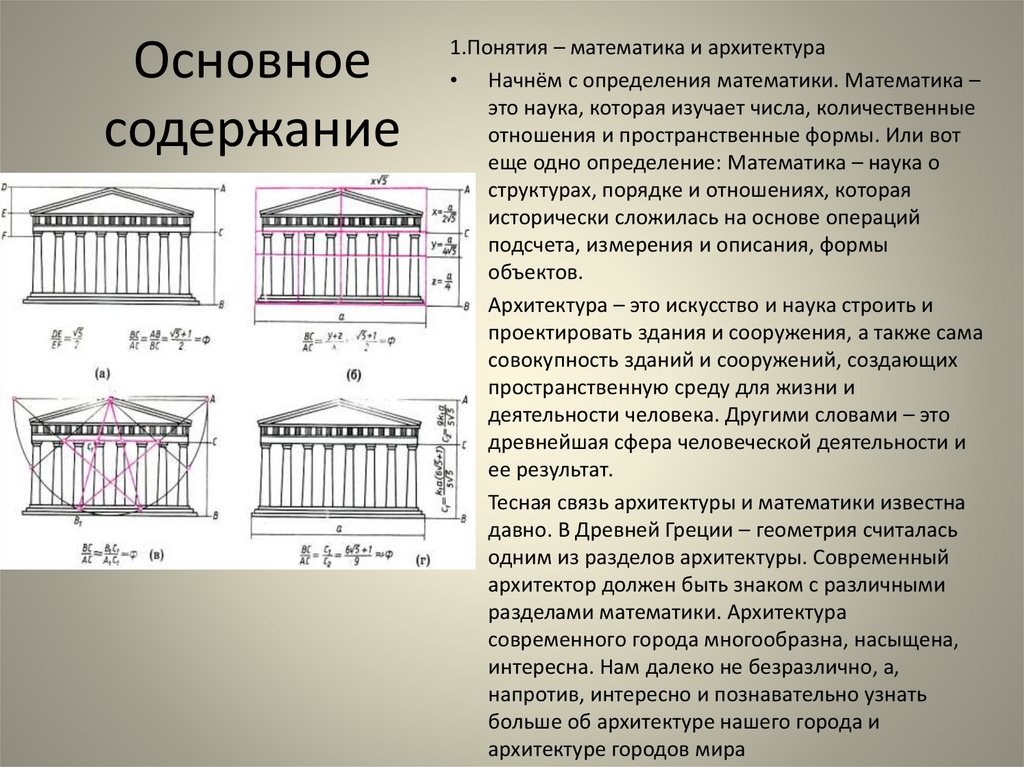
1.Понятия – математика и архитектура
• Начнём с определения математики. Математика –
это наука, которая изучает числа, количественные
отношения и пространственные формы. Или вот
еще одно определение: Математика – наука о
структурах, порядке и отношениях, которая
исторически сложилась на основе операций
подсчета, измерения и описания, формы
объектов.
• Архитектура – это искусство и наука строить и
проектировать здания и сооружения, а также сама
совокупность зданий и сооружений, создающих
пространственную среду для жизни и
деятельности человека. Другими словами – это
древнейшая сфера человеческой деятельности и
ее результат.
• Тесная связь архитектуры и математики известна
давно. В Древней Греции – геометрия считалась
одним из разделов архитектуры. Современный
архитектор должен быть знаком с различными
разделами математики. Архитектура
современного города многообразна, насыщена,
интересна. Нам далеко не безразлично, а,
напротив, интересно и познавательно узнать
больше об архитектуре нашего города и
архитектуре городов мира

5.

2. Как математика помогает добиться прочности
сооружений
• Прочность сооружения обеспечивается не только
материалом, из которого оно создано, но и
конструкцией, которая используется в качестве
основы при его проектировании и строительстве.
Прочность сооружения напрямую связана с той
геометрической формой, которая является для
него базовой.
• Камень плохо работает на изгиб, но хорошо
работает на сжатие. Это привело к использованию
в архитектуре арок и сводов. Так возникла новая
арочно-сводчатая конструкция. С появлением
арочно-сводчатой
конструкции в архитектуру прямых линий и
плоскостей, вошли окружности, круги, сферы и
круговые цилиндры. Первоначально в архитектуре
использовались только полуциркульные арки или
полусферические купола.

6.

3.Геометрические формы в разных
архитектурных стилях
• Ни один из видов искусств так тесно
не связан с математикой, а точнее с
ее разделом геометрия, как
архитектура.
• Архитектурные произведения
живут в пространстве, являются его
частью, вписываясь в
определенные геометрические
формы. Кроме того, они состоят из
отдельных деталей, каждая из
которых также строится на базе
определенного геометрического
тела. Часто геометрические формы
являются комбинациями различных
геометрических тел.
• Геометрическая форма сооружения
настолько важна, что бывают
случаи, когда в имени или названии
здания закрепляются названия
геометрических фигур.

7.

4.Симметрия – царица архитектурного
совершенства
• Наиболее распространенный вид
симметрии в архитектуре – зеркальный,
когда правая половина строения повторяет
левую.
• «Симметрия» в переводе с греческого
языка означает «соразмерность,
пропорциональность, одинаковость
расположения частей». Архитектурные
сооружения, созданные человеком, в
большей своей части симметричны. Они
приятны для глаза, их люди считают
красивыми.
Кроме симметрии в архитектуре можно
рассматривать асимметрию и
диссимметрию.
• Асимметрия – это противоположность
симметрии, ее отсутствие.
• Диссимметрия – это частичное отсутствие
симметрии, расстройство симметрии,
выраженное в наличии одних
симметричных свойств и отсутствии
других.

8.

5. Золотое сечение в архитектуре.
• Золотое сечение – это такое
пропорциональное деление
отрезка на неравные части, при
котором весь отрезок так
относится к большей части, как
сама большая часть относится к
меньшей
• В книгах о “золотом сечении”
можно найти замечание о том,
что в архитектуре, как и в
живописи, все зависит от
положения наблюдателя, и что,
если некоторые пропорции в
здании с одной стороны
кажутся образующими “золотое
сечение”, то с других точек
зрения они будут выглядеть
иначе.

9.

Заключение
• Все сказанное убеждает нас в том, что архитектура и математика, на
протяжении веков активно влияли друг на друга. Они давали друг другу
новые идеи и стимулы, совместно ставили и решали задачи. По сути,
каждую из этих дисциплин можно рассматривать существенным и
необходимым дополнением другой.
• За длительный период человеческой цивилизации создано немало
произведений исключительной красоты. Эти произведения могут
явиться примером использования зодчим в своем творческом труде
математических закономерностей (в том числе симметрии,
асимметрии, диссимметрии и золотого сечения). Математика помогает
добиться прочности, удобства и красоты архитектурных сооружений за
счет разнообразных геометрических фигур и форм. В том числе и в
городе Новосибирске, архитектура развивается по этим же
математическим законам. Всё чаще архитекторы Новосибирска ищут
новые необычные формы для своих зданий, поэтому город постепенно
преображается. На этом можно завершить мою работу. Гипотеза
подтверждена.
• Единство науки и искусства – важнейший залог последующего развития
культуры.

10.

Список источников информации
• 1.Аксенова М. Энциклопедия для детей Аванта+. – 1998. – Т. 11,
– 621с.
• 2.Волошинов А.В. Математика и искусство. – М.: Просвещение,
2000. – 339с.
• 3.Памятники истории, архитектуры и монументального
искусства Новосибирской области. Каталог. – Н., Научнопроизводственный центр по сохранению историко-культурного
наследия Новосибирской области, 2003. –278с.
• 4.Степанов А.В. Объёмно - пространственная композиция. М.:
Архитектура-С. – 2004. – 256с.
• 5.Общероссийский математический портал Math-Net.Ru
http://www.mathnet.ru 6. Портал Allmath.ги - вся математика в
одном месте http://www.allmath.ru