Курс лекций «Дискретная математика»

1.

Курс лекций «Дискретная математика»
Ф.И. Каган, к.ф.-м.н., доцент,
Заслуженный работник культуры РФ
05
БУЛЕВА АЛГЕБРА И ЕЕ ИНТЕРПРЕТАЦИИ

2.

5.1. Булева алгебра и ее интерпретации
Обнаруженное нами полное подобие (изоморфность) между алгеброй
высказываний и алгеброй множеств иллюстрирует очень важный принцип
взаимодействия математики со всеми возможными областями ее применений.
Этот принцип состоит в следующем. Математика вводит в рассмотрение,
изучает, развивает абстрактные математические структуры, для которых рано
или поздно находятся очень разные по своей сущности явления природы,
техники, жизни общества, гуманитарной сферы, функционирование которых
подчиняется законам, описываемым абстрактной математической структурой.
Так что получается, что абстрактная математическая структура становится
математической моделью для самых разных явлений и процессов. А эти явления
и процессы, в свою очередь, становятся конкретными интерпретациями той или
иной абстрактной математической структуры.
Булева алгебра – это математическая структура, названная в честь
английского математика и логика 19 века Джорджа Буля, одного из пионеров
создания математической логики.
Булевой алгеброй называется непустое множество A с двумя бинарными
операциями (аналогами конъюнкции и дизъюнкции), одной унарной операцией
(аналогом отрицания) и двумя выделенными элементами (аналогами констант 0
(ложь) и 1 (истина)), так что для любых элементов из этого множества
выполняются известные нам соотношения, из которых могут быть отобран в
качестве аксиом булевой алгебры тот или иной набор из этих соотношений.

3.

5.2. Алгебра релейно-контактных схем
К уже известным нам алгебре высказываний и алгебре множеств может быть
добавлена еще одна интерпретация булевой алгебры – алгебра релейноконтактных схем. Впервые идея использования алгебры логики для построения
автоматических устройств была выдвинута в 1910 году известным физиком
П. Эренфестом. Но только в 30-х годах эта идея нашла свое воплощение в работах
советского физика В.И. Шестакова, американского математика К. Шеннона и
японского инженера А. Накосима.
Контактная схема представляет собой устройство из проводников и
контактов, связывающих полюса источника тока. Контакт бывает в двух
состояниях: контакт разомкнут, это состояние кодируется нулем; и контакт
замкнут, состояние кодируется 1.
Контакт «не Х» (Х) – это контакт, который работает в противоположном
режиме с Х, т.е. когда контакт Х замкнут, контакт Х обязательно разомкнут.
Дизъюнкции ставится в соответствие схема, состоящая из параллельного
соединения контактов X, Y, так как цепь будет замкнута тогда и только тогда,
когда замкнут хотя бы один из контактов.

4.

Конъюнкции
ставится
в
соответствие
схема,
состоящего
из
последовательного соединения контактов X, Y, так как цепь будет замкнута тогда
и только тогда, когда замкнуты оба контакта одновременно.
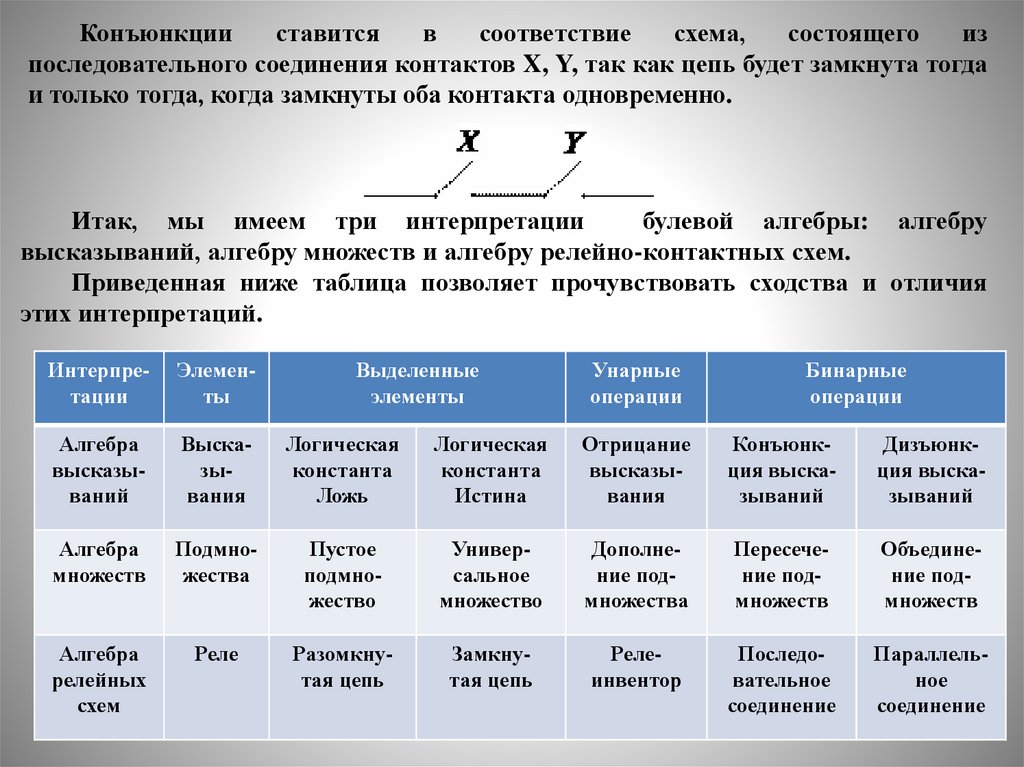
Итак, мы имеем три интерпретации
булевой алгебры: алгебру
высказываний, алгебру множеств и алгебру релейно-контактных схем.
Приведенная ниже таблица позволяет прочувствовать сходства и отличия
этих интерпретаций.
Интерпретации
Элементы
Выделенные
элементы
Унарные
операции
Бинарные
операции
Алгебра
высказываний
Высказывания
Логическая
константа
Ложь
Логическая
константа
Истина
Отрицание
высказывания
Конъюнкция высказываний
Дизъюнкция высказываний
Алгебра
множеств
Подмножества
Пустое
подмножество
Универсальное
множество
Дополнение подмножества
Пересечение подмножеств
Объединение подмножеств
Алгебра
релейных
схем
Реле
Разомкнутая цепь
Замкнутая цепь
Релеинвентор
Последовательное
соединение
Параллельное
соединение

5.

Из этих трех интерпретаций наиболее удобна для анализа алгебра
высказываний, так что она широко использовалась и используется для анализа и
синтеза релейно-контактных схем, которые востребованы в телефонии,
телеуправлении, автоматике и телемеханике, на железнодорожном транспорте, в
вычислительной технике, при проектировании и оптимизации интегральных
схем и микропроцессорных систем.
Примеры применения алгебры высказываний для упрощения релейных схем
будут рассмотрены на практических занятиях.
Существуют разные системы аксиом для определения булевой алгебры. При
этом остальные соотношения, которые естественно возникают при рассмотрении
разных ее интерпретаций, выводятся из аксиом.
Ниже приводится один из вариантов аксиом булевой алгебры, удобный для
приложений.
(a ˄ b) ˄ c = a ˄ (b ˄ c)
(a ˅ b) ˅ c = a ˅ (b ˅ c)
ассоциативность
a˄b=b˄a
a˅b=b˅a
коммутативность
a ˄ (a ˅ b) = a
a ˅ (a ˄ b) = a
законы поглощения
a ˄ (b ˅ c) = (a ˄ b) ˅ (a ˄ c)
a ˅ (b ˄ c) = (a ˅ b) ˄ (a ˅ c)
дистрибутивность
a˄¬a=0
a˅¬a=1
дополнительность
Булева алгебра вместе с рассмотренными выше числовыми системами дает
исходный материал для обращения к общим, так называемым алгебраическим
структурам и иным по своей природе математическим структурам, на которых
основано современное здание математики и ее многочисленные приложения в
самых разных отраслях человеческого знания, в том числе и в современных
информационных системах и технологиях.