Напряженно-деформированное состояние оболочечных конструкций, выполненных из материалов с усложненными механическими свойствами

1.

Тульский государственный университет
Кафедра «Строительство, строительные материалы и конструкции»
ТЕЛИЧКО Виктор Григорьевич
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
ОБОЛОЧЕЧНЫХ КОНСТРУКЦИЙ, ВЫПОЛНЕННЫХ ИЗ МАТЕРИАЛОВ
С УСЛОЖНЕННЫМИ МЕХАНИЧЕСКИМИ СВОЙСТВАМИ
Специальность 01.02.04 - механика деформируемого
твердого тела
Диссертация на соискание ученой степени
кандидата технических наук
Научный руководитель
д. т. н., профессор Трещев А.А.

2. Типы потенциалов деформаций

W1 Aе Bе Cе Dе Eе Сos3 Aр Bр 2 C р Dр E р Сos3 2
2
2
W2 Aе Bе Cе Dе Eе Aр Bр 2 C р Dр E р 2
2
2
W3 Aе 2 Cе 2 C р Dр E р 2
ij ij / 3,
Sij Sij / 3,
n
n
n
1
2
3
Sij ij ij , Сos / S0 ,
Sin / S0 , S0 2 2 , Cos3 2 det( Sij ) / 3 ,
4
eij 2C1 ij / 3 2 A1 C1 ij / 3 Tij
W1 Tij Tij , , ij , W 2 ,W 3 Tij Tij , ij
ij 2G eij Tij 3 e T ij
5
2G 3/ 2Cе , Cе Aе / 2 AеCе , 3T Tij ij , 3e eij ij
W1 : e / 3K 0 / 3D0 ,
э 1 tg 2 / 2G0 / 3D0 ,
tg 3R sin 3 / 3 / 2G0 / D0
6
7
8
W1 ,W 2 :
e / 3K 0 / 3D0 ,
э / 2G0 / 3D0
9
10

3.

Типы потенциалов деформаций (продолжение)
Обобщенный модуль объемных деформаций
K 0 1/ 2 Ae Be (2 2 ) Ee 3Сos3
n[( Ap B p ) 2 (С р D p E p Cos3 ) 2 ]n 1
11
[2 Ap B p (2 2 ) E p 3Cos3 ] ;
Обобщенный модуль формоизменения (сдвига)
2G0 3/{(2 De Be ) 3 2Ce Ee Cos3 (2 2 )
n[( Ap B p ) 2 (C p D p E p Cos3 ) 2 ]n 1
12
[(2 D p B p ) 3 2C p E p Cos3 (2 2 )]};
Обобщенный модуль дилатации
D0 1/{De 3 n[( Ap B p ) 2 (C p D p E p Cos3 ) 2 ]n 1 D p 3};
R Eе nЕ р Aр B р 2 C р D р E р cos3 2
n 1
.
13
14

4.

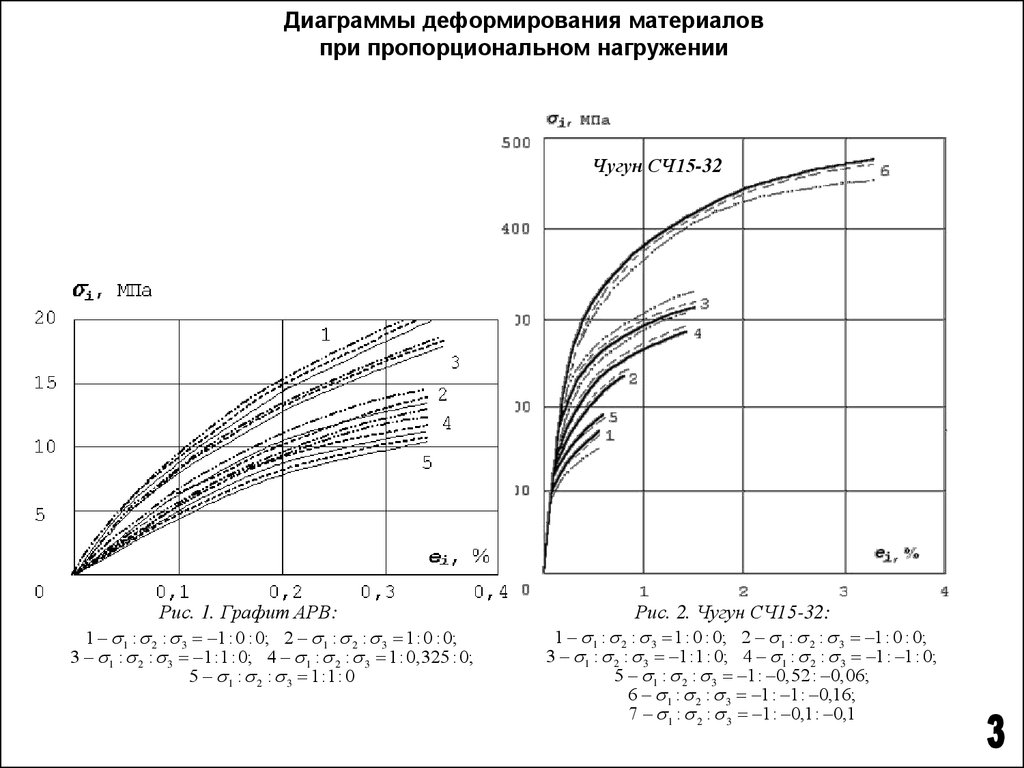
Диаграммы деформирования материалов
при пропорциональном нагружении
Чугун СЧ15-32
Рис. 1. Графит АРВ:
1 – 1 : 2 : 3 1: 0 : 0; 2 – 1 : 2 : 3 1: 0 : 0;
3 – 1 : 2 : 3 1:1: 0; 4 – 1 : 2 : 3 1: 0,325 : 0;
5 – 1 : 2 : 3 1:1: 0
Рис. 2. Чугун СЧ15-32:
1 – 1 : 2 : 3 1: 0 : 0; 2 – 1 : 2 : 3 1: 0 : 0;
3 – 1 : 2 : 3 1:1: 0; 4 – 1 : 2 : 3 1: 1: 0;
5 – 1 : 2 : 3 1: 0,52 : 0,06;
6 – 1 : 2 : 3 1: 1: 0,16;
7 – 1 : 2 : 3 1: 0,1: 0,1

5.

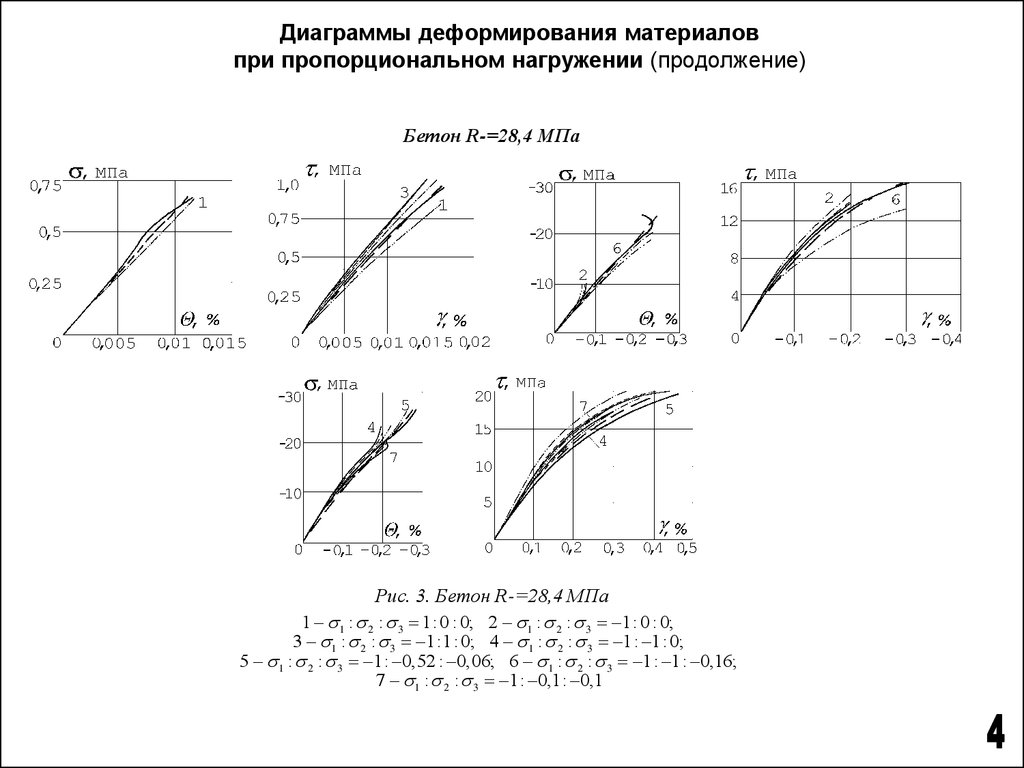
Диаграммы деформирования материалов
при пропорциональном нагружении (продолжение)
Бетон R-=28,4 МПа
Рис. 3. Бетон R-=28,4 МПа
1 – 1 : 2 : 3 1: 0 : 0; 2 – 1 : 2 : 3 1: 0 : 0;
3 – 1 : 2 : 3 1:1: 0; 4 – 1 : 2 : 3 1: 1: 0;
5 – 1 : 2 : 3 1: 0,52 : 0,06; 6 – 1 : 2 : 3 1: 1: 0,16;
7 – 1 : 2 : 3 1: 0,1: 0,1

6.

Основные уравнения и зависимости
U 1 x1 , x 2 , x 3 u1 x1 , x 2 x 3 2 x1 , x 2 ;
U 2 x1 , x 2 , x 3 u 2 x1 , x 2 x 3 1 x1 , x 2 ;
U 3 x1 , x 2 , x 3 w x1 , x 2 ;
1 w'2 23 ; 2 w'1 13 .
N11,1 N12,2 0; N12,1 N 22,2 0;
M11,1 M12,2 Q 1; M12,1 M 22,2 Q2 ;
Q1,1 Q 2,2 q.
e11 u1,1 x3 2,1 ; e 22 u 2,2 x3 1,2 ;
e33 0;
15
12 u1,2 u 2,1 x 3 2,2 1,1 ;
13 2 w'1 ; 23 1 w'2 .
16
B e
18
17
h/2
Qk
k3
d x 3 , k 1,2
19
h / 2
D11
M 11
M
22
M 12
Q1
M
; D
Q2
N11
N 22
N12
D12
D22
D16
D26
D66
K 14
K 24
K 64
C 44
Sim
h/2
C km
K 15
K 25
K 65
C 45
C 55
h / 2
K 11
K 12
K 16
C14
C15
K 12
K 22
K 26
C 24
C 25
C11
C12
C 22
K 16
2,1
K 26
1
,2
2,2 1,1
K 66
C 46
13
;
;
C 65
23
u1,1
C16
C 26
u 2,2
u1,2 u 2,1
C 66
h/2
Bkm d x 3 ; K km
h / 2
h/2
Bkm x 3 d x 3 ; Dkm
h / 2
B km x 32 d x 3 .
20
21

7.

Вывод матрицы жесткости конечного элемента
M P 22
D M E M 23
1
T
T
П U n t d S t d S
n
Vn
S
U
1
T
M E M d S
2S
t L q 26
25
R 27
T
T
T
1
П H T q 0 q
n 2
11 , 13 , 15 , 16 14
T R L d S
T
H P E P d S 29
0 L d S
30
T
T
Vn
S
1
n
K T H T
T
1
33
1
34
1
M P H T q 35
M 11 1 4 x1 9 x 2 ; M 22 2 5 x 2 10 x1 ; M 12 3 12 x1 11 x 2 ;
Q1 4 11; Q2 5 12 ; N11 6 ; N 22 7 ; N12 8
1 2 3 4 5 6 7 8 9 10 11 12
12
31
32
n
H T q
22 P M
28
S
T H T q 0
T
24
T
N 12 37 H 12 12
36
37

8.

M 11 M 11C ij M 12 S ij ; M 22 M 22 S ij M 12Cij ; N 11 N 11C ij N 12 S ij ;
38
N 22 N 22 S ij N 12C ij ; Q Q1C ij Q2 S ij , C ij cos ij ; S ij sin ij
1
Aij Lij [ Q1C ij Q2 S ij w M 12C ij M 22 S ij 1 M 12 S ij M 11C ij 2
0
39
N 11C ij N 12 S ij u1 N 22 S ij N 12C ij u 2 ] d
A A12 A23 A31
qi wi 1i 2i u1i u 2i qi1 qi 2 qi3 qi 4 qi5
T
T
41
q q1 q 2 q 3 ... q15
T
40
42
w 1 wi w j Lij 1 i j / 2;
1 1 1i 1 j ; 2 1 2i 2 j ;
u1 1 u1i u1 j ; u 2 1 u 2i u 2 j ;
43
i 1i cij 2i S ij ; j 1 j cij 2 j S ij ; Lij
x1 x1i Lij s ij ; x 2 x 2i Lij cij
(36), 39 , 43 , 44 40 42 T q T
12 15
44

9.

Оценка сходимости разработанной конечно-элементной модели
а)
б)
Рис. 4. Сходимость решения по максимальным прогибам пластины, опертой по контуру:
а – в середине шарнирно опертой; б – в середине жесткозащемленной
Рис. 5. Сходимость решения по максимальным моментам для пластин рис. 4
w0 , M 0 – точное решение; w1 , M 1 – КЭ-решение в модификациях H12, H 9

10.

Оценка сходимости разработанной КЭ-модели (продолжение)
Рис. 6. Оценка сходимости решения
для жесткозащемленной по контуру плиты

11.

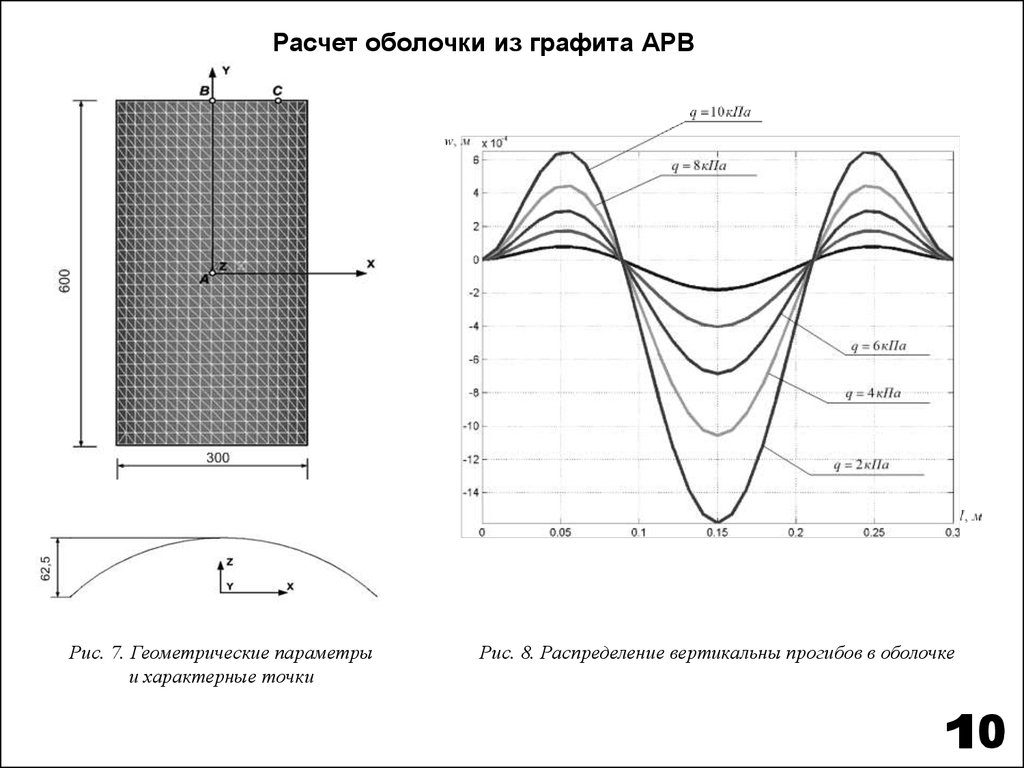
Расчет оболочки из графита АРВ
Рис. 7. Геометрические параметры
и характерные точки
Рис. 8. Распределение вертикальны прогибов в оболочке

12.

Расчет оболочки из графита АРВ (продолжение)
Построенная модель
Классическая теория
q, кПа
q, кПа
Классическая теория
Построенная модель
Точка А
Точка C
w, м
w, м
Точка B
Рис. 9. График вертикальных прогибов в характерных точках

13.

Моделирование фиктивных слоев
(дополнительные технические гипотезы)
1. Нагружение простое, деформация активная.
2. Деформации ползучести бетона на учитываются.
3. Размеры оболочек в плане велики по сравнению со средним расстоянием между
арматурными стержнями.
4. В качестве модели для стальной арматуры примем идеальное упругопластическое тело,
воспринимающее только нормальные напряжения в поперечных сечениях, а ее
коэффициенты Пуассона примем равными нулю.
5. Напряжения в пределах армированных слоев оболочки определим как сумму напряжений в
бетоне и арматуре, а за условие совместности бетона и арматуры примем равенство
деформаций этих двух сред.
6. Срединную поверхность оболочки представим сетью гибридных конечных элементов
модификации Н12 с учетом разбиения по толщине на ряд фиктивных слоев .
7. Жесткостные характеристики, рассчитанные для центра фиктивного слоя данного конечного
элемента, распространим на все точки слоя.
8. Критерий прочности бетона в каждом фиктивном слое – по П.П. Баландину.
9. Трещины нормальны к срединной поверхности оболочки в точке трещинообразования,
главные напряжения вычисляются по формулам плоского напряженного состояния.
10. Трещины в области треснувшего фиктивного слоя будем считать сквозными и
параллельными друг другу. Влияние растянутого бетона учитывается по В.И. Мурашеву.
11. При наличии трещин бетон моделируем трансверсально-изотропным телом с плоскостью
изотропии, параллельной плоскости трещин.

14.

Моделирование фиктивных слоев (продолжение)
Бетонные слои
без трещин:
Армированные
(железобетонные) слои:
Бетонные слои
с трещиной :
Железобетонные
слои с трещиной :
e A
1
B A
45
0
0 0
B S 11
B S 22 0 0
1
0 0
B A BS 47 BS
sim
0
Критерий прочности П.П. Баландина:
0
0
0
0
0
1
46
BS11 E S 11;
BS 22 E S 22
11 ASi / S i11 hS ,
22 Asi / S i 22 hS
112 222 3 122 232 132 11 22 Rbt Rb 11 22 R bt Rb 0
B 0
B211 B2 22 3 122 232 132 B11 B 22
48
49
50
Rbt Rb B11 B 22 R bt Rb 0
1 arctg[( 1t B11 ) / 12 ] Направления развития трещин
1 X 1*OX 2* , X 1 OX 2
e A
*
22
*
12
*
B11
A
*
22
*
B 22
*
B 22
E B 1/ A , B A / A ;
*
22
*
12
*
22
B
*
B11
/ E
B
e A
*
*
*
B
51
52

15.

e11*
A11* A12*
B* 11
0
0
0
*
*
*
e
A
0
0
0
22
22
B 22
*
*
A66
0
0 ; B B* 12 ;
e * 12* ; A*
*
*
*
Sim
A
0
13
44
B13
*
*
*
A55
23
B 23
*
0 1: A11* 1/ EB ; A12* B / E B ; A22
1/ E B ;
*
*
*
A44
A66
2 1 B / EB ; A55
2 1 / E B ;
Железобетонные
слои с трещиной
(продолжение) :
E S11 11
C
BS
0
E S 22 22
Sim
0 0 0
0 0 0
0 0 0 для арматуры в X 1 OX 2
0 0
0
B BBC BSC ,
В.И. Мурашев: S E sn / E B E sn
55 , 56 E
S 11
55
BBC A C
11 cos 4 1 E S 22 22 sin 4 1 1/ s 1 / E B
B e B e B cos B e
48
B e B e B sin 2 0,7 R
C
B16 11
C
B12 22
C
B 26 26
C
B16
2
12
C
B 66
C
B12 12
1
12
1
54
Esn E S11 11 cos 4 1 E S 22 22 sin 4 1
*
Г.А. Гениев, В.Н. Киссюк, Г.А. Тюпин: S 1 0,7 Rbt / 11
C
B11 11
1
bt
58
при *B11 0,7 Rbt
C
BBC22 e22 B26
12 sin 2 1
60
53
A C , s , B , s
56
57
59

16.

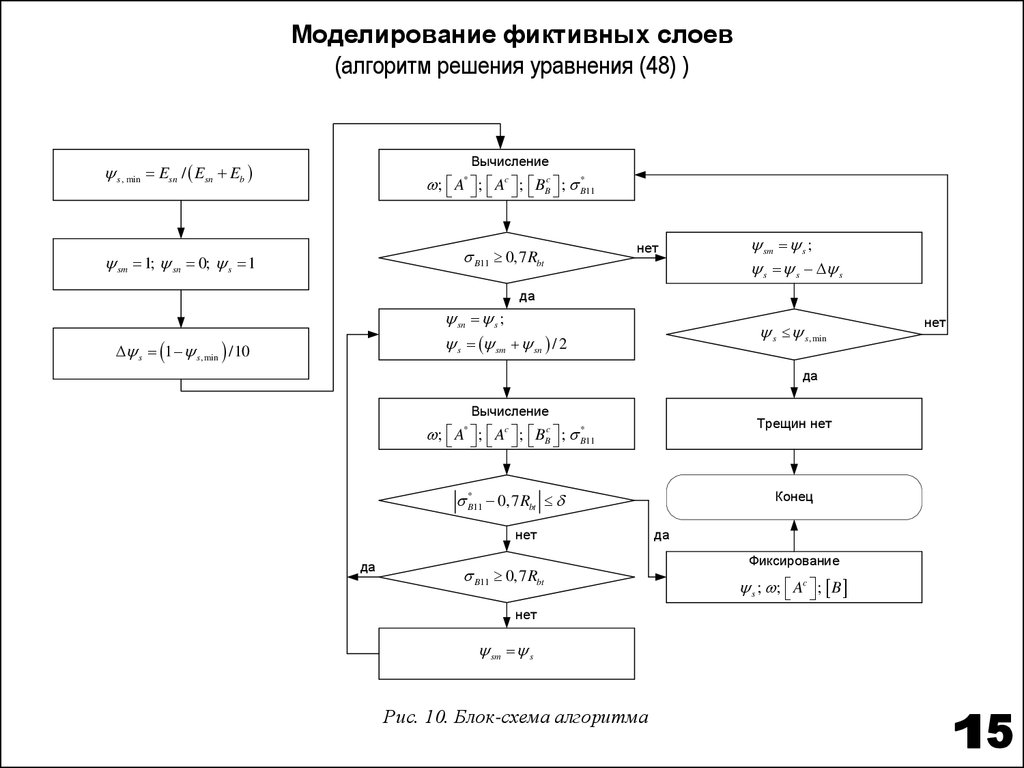
Моделирование фиктивных слоев
(алгоритм решения уравнения (48) )
Вычисление
s , min Esn / Esn Eb
; A ; Ac ; BBc ; B*11
*
B11 0,7 Rbt
sm 1; sn 0; s 1
нет
sm s ;
s s s
да
sn s ;
s s , min
s sm sn / 2
s 1 s , min /10
да
Вычисление
; A ; Ac ; BBc ; B*11
Трещин нет
B* 11 0,7 Rbt
Конец
*
нет
да
B11 0,7 Rbt
нет
sm s
Рис. 10. Блок-схема алгоритма
да
Фиксирование
s ; ; Ac ; B
нет

17.

Моделирование фиктивных слоев (окончание )
Железобетонные слои
с пересекающимися
трещинами:
B BSC
BSC 42
Алгоритм решения задачи
об определении НДС армированных оболочек
из материалов с усложненными свойствами
1.
2.
3.
4.
5.
6.
Формирование задания на расчет конструкции.
Формирование матрицы связи узлов конечных элементов.
Формирование граничных условий.
Задание нагружения оболочки.
Формирование матриц жесткости конечных элементов.
Расчет вектора узловых перемещений.
Повышение помехозащищенность вычислительного
процесса
Возможность искусственно прервать ход решения для:
- оценки динамику сходимости,
- корректировки дальнейшего вычислительного процесса,
- продолжения процесса с прерванной операции.
61

18.

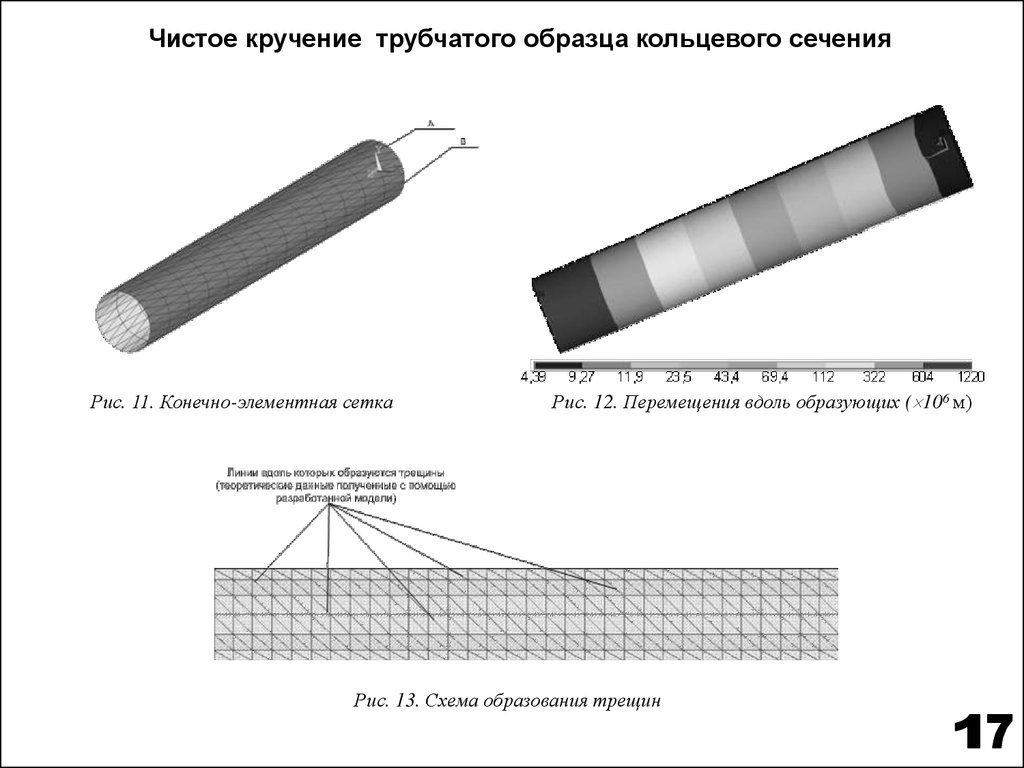
Чистое кручение трубчатого образца кольцевого сечения
Рис. 11. Конечно-элементная сетка
Рис. 12. Перемещения вдоль образующих ( 106 м)
Рис. 13. Схема образования трещин

19.

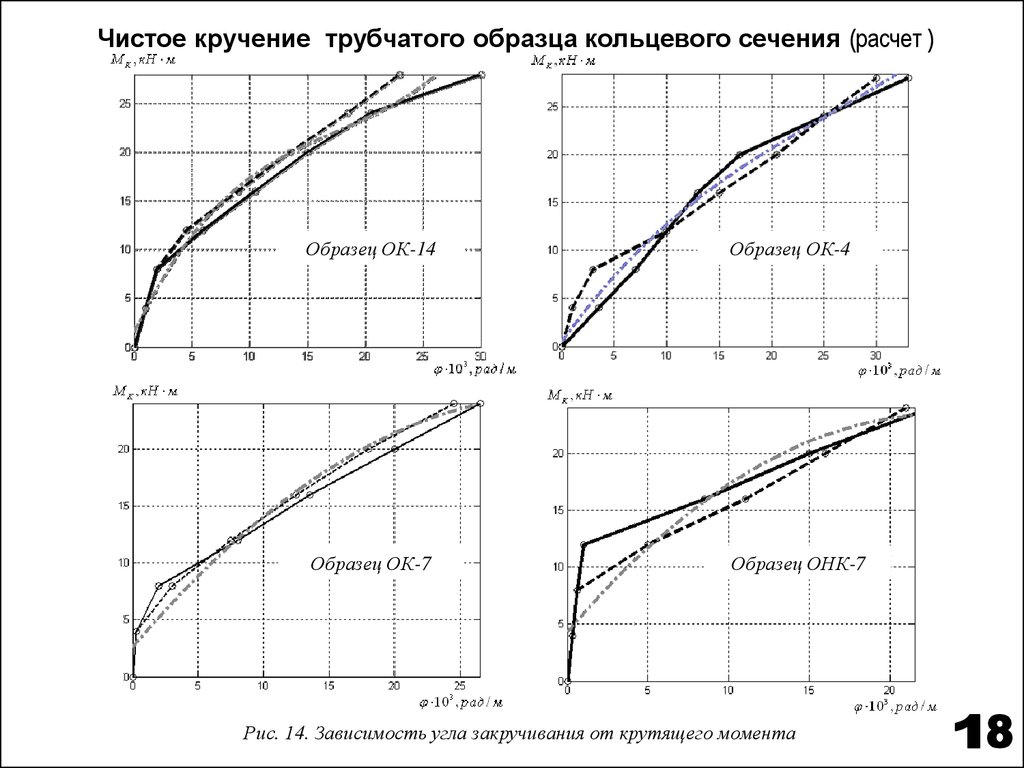
Чистое кручение трубчатого образца кольцевого сечения (расчет )
Образец ОК-14
Образец ОК-4
Образец ОК-7
Образец ОНК-7
Рис. 14. Зависимость угла закручивания от крутящего момента

20.

Цилиндрическая железобетонная оболочка
(размеры в плане 24х12 м, высота подъема 2,5 м, жесткое защемление по образующим)
q, кПа
Момент трещинообразования
w, м
Рис. 15. Конечно-элементная сетка
Рис. 16. График вертикальных прогибов
w(q) в центре плана оболочки
w, м 10 2
w, м 10 2
7 кПа
14 кПа
7 кПа
14 кПа
21 кПа
21 кПа
28 кПа
35 кПа
35 кПа
28 кПа
l, м
l, м
Рис. 17. Распределение вертикальных
прогибов вдоль длинной оси
Рис. 18. Распределение вертикальных
прогибов вдоль диагонали плана

21.

Цилиндрическая железобетонная оболочка (продолжение)
Рис. 19. Распределение сверху
напряжений вдоль диагонали плана
(нагрузка 35 кПа)
Нагрузка
21 кПа
Рис. 20. Распределение снизу
напряжений вдоль диагонали плана
(нагрузка 35 кПа)
Нагрузка
28 кПа
Рис. 21. Развитие трещин в оболочке
Нагрузка
35 кПа

22.

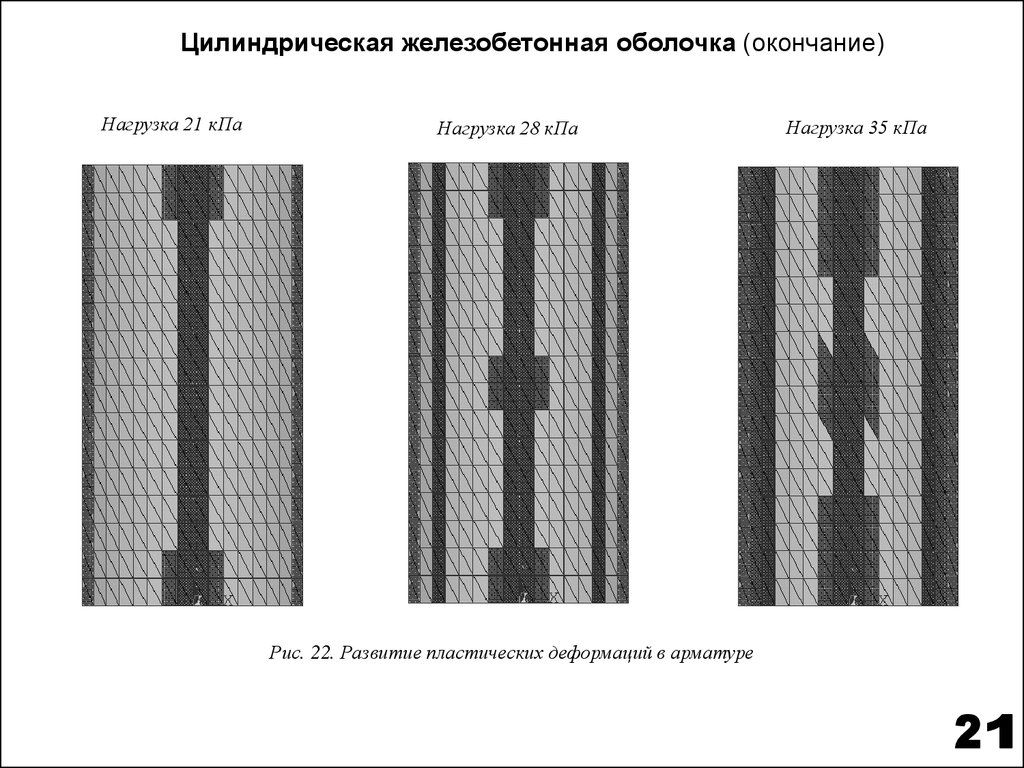
Цилиндрическая железобетонная оболочка (окончание)
Нагрузка 21 кПа
Нагрузка 28 кПа
Рис. 22. Развитие пластических деформаций в арматуре
Нагрузка 35 кПа

23.

Цилиндрическая железобетонная оболочка
(размеры в плане 6х12 м, высота подъема 1,8 м, шарнирное опирание по образующим)
, Па 10 3
Сверху
2,2 кПа
4,4 кПа
6,6 кПа
8,8 кПа
Снизу
11 кПа
l, м
Рис. 23. Распределение напряжений 11 вдоль диагонали плана оболочки
Сверху
Снизу
Рис. 24. Распределение напряжений 12 вдоль диагонали плана оболочки

24.

Цилиндрическая железобетонная оболочка (окончание)
Первичные трещины
Первичные трещины
Первичные трещины
Первичные трещины
Первичные трещины
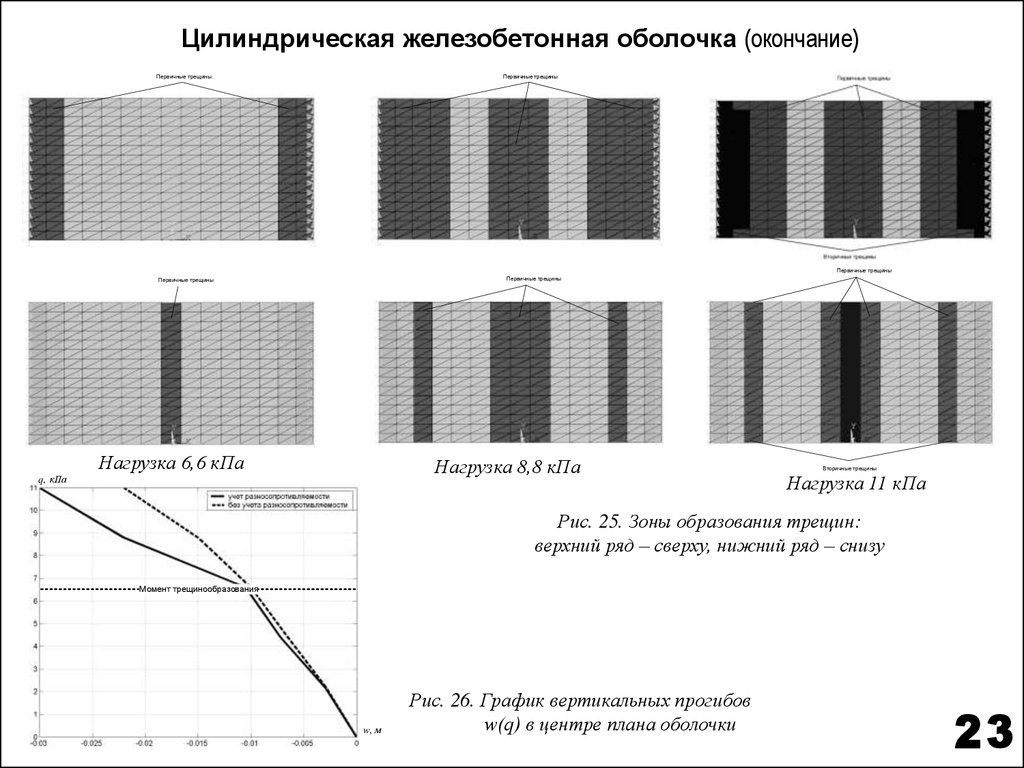
Нагрузка 6,6 кПа
Нагрузка 8,8 кПа
q, кПа
Вторичные трещины
Нагрузка 11 кПа
Рис. 25. Зоны образования трещин:
верхний ряд – сверху, нижний ряд – снизу
Момент трещинообразования
w, м
Рис. 26. График вертикальных прогибов
w(q) в центре плана оболочки

25.

Оболочка положительной гауссовой кривизны
(размеры в плане 24х24 м, высота подъема 6 м)
Рис. 27. Картина распределения вертикальных
перемещений w (м) по поверхности оболочки
q, кПа
Рис. 28. Распределение вертикальных прогибов w
вдоль диагонали плана оболочки
q, кПа
Результаты с учетом
преднапряжения нижнего
пояса фермы
Результаты с учетом
преднапряжения нижнего
пояса фермы
Результаты без учета
преднапряжения нижнего
пояса фермы
Результаты без учета
преднапряжения нижнего
пояса фермы
Момент трещинообразования
Момент трещинообразования
w, м
Рис. 29. График вертикальных прогибов
w(q) в центре плана оболочки
w, м
Рис. 30. График вертикальных прогибов
в точке max w(q)

26.

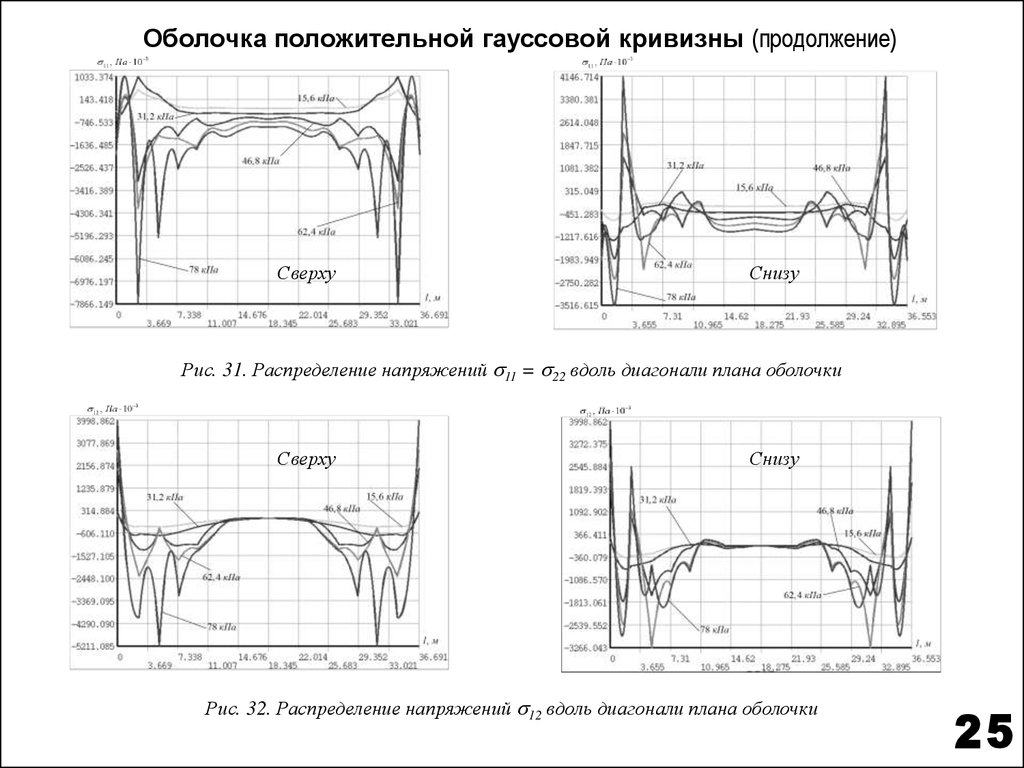
Оболочка положительной гауссовой кривизны (продолжение)
Сверху
Снизу
Рис. 31. Распределение напряжений 11 = 22 вдоль диагонали плана оболочки
Сверху
Снизу
Рис. 32. Распределение напряжений 12 вдоль диагонали плана оболочки

27.

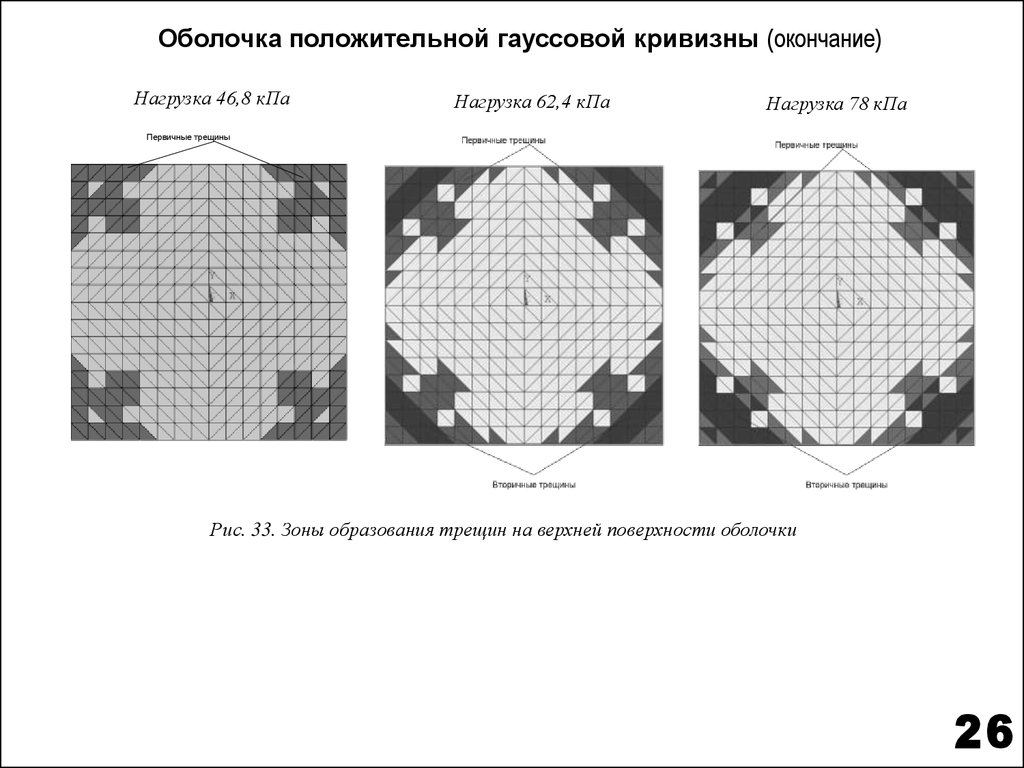
Оболочка положительной гауссовой кривизны (окончание)
Нагрузка 46,8 кПа
Нагрузка 62,4 кПа
Нагрузка 78 кПа
Первичные трещины
Рис. 33. Зоны образования трещин на верхней поверхности оболочки

28.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1. Проведенные исследования позволили получить новое решение научно-технической
задачи механики деформируемого твердого тела, заключающееся в разработке
математической модели и программного комплекса, ориентированных на решение задач по
исследованию НДС элементов макрооднородных и армированных оболочечных конструкций,
выполненных из разносопротивляющихся материалов, с учетом трещинообразования и
пластических деформаций в арматуре. Получены решения для оболочек, которыми
подтверждено наличие известных фактов и обнаружены новые количественные и
качественные эффекты деформирования. В частности показано, что в стадии работы
конструкции с трещинами на ее жесткость и прочность существенное влияние оказывает
процессы образования, распространения трещин и переход арматуры в пластическую область
работы. С другой стороны полученные решения свидетельствуют о необходимости учета
нелинейной разносопротивляемости бетона на всех стадиях работы железобетонной
конструкции.
2. В рамках нормированных пространств напряжений, предложенных в работах
Н.М.Матченко, Л.А.Толоконникова и А.А.Трещева проанализированы подходы к построению
определяющих соотношений деформационной теории структурно изотропных
упругопластических дилатирующих материалов, чувствительных к виду напряженного
состояния. Для использования в прикладных исследованиях выделен наиболее
универсальный вариант потенциала деформаций. Проанализированы вытекающие из
принятых уравнений состояния законы изменения объема, формы и фазовая характеристика.

29.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ (продолжение)
3. Построен плоский треугольный гибридный конечный элемент, обеспечивающий решения
задач об исследовании НДС элементов оболочечных конструкций, выполненных из
материалов с усложненными свойствами. Модифицирована классическая конечно-элементная
модель стержня для учета усложненных свойств и трещинообразования.
4. Разработана математическая модель решения задачи об определении НДС оболочечных
конструкций разной геометрической конфигурации, выполненных из макрооднородных
материалов, обладающих физической нелинейностью. В основу этой модели положен метод
многослойных конечных элементов.
5. На базе модифицированной пошагово-итерационной процедуры решения нелинейных
задач разработан и запрограммирован алгоритм определения характеристик НДС
оболочечных конструкций.
6. С использование разработанного программного обеспечения решен ряд задач по
определению характеристик НДС:
• трубчатых железобетонных элементов при чистом кручении;
• цилиндрической оболочки, выполненной из макрооднородного разносопротивляющегося
материала. В качестве конкретного материала был принят графит марки АРВ;
• жестко защемленной вдоль образующих и свободно опертой вдоль образующих
цилиндрических оболочек;
• оболочки положительной гауссовой кривизны прямоугольной в плане опертой на фермы
по контуру.

30.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ (окончание)
– для трубчатых железобетонных элементов при чистом кручении проведено сравнение с
экспериментальными данными и теорией Н.И. Карпенко, получено хорошее совпадение
результатов;
– цилиндрической оболочки выполненной из макрооднородного разносопротивляющегося
материала. В качестве конкретного материала был принят графит марки АРВ. Результаты
расчета показали, что за счет учета разносопротивляемости удалось получить уточнение
результатов, по сравнению с «классической теорией» оболочек до 33% для перемещений и
углов поворота и в среднем до 50% для напряжений;
– жестко защемленной вдоль образующих и шарнирно опертой вдоль образующих
цилиндрических оболочек. Анализ результатов их расчета показал, что учет усложненных
свойств существенен при проведении статических расчетов. В частности, для перемещений
различия составили до 70% по сравнению с расчетами без учета усложненных свойств бетона.
– оболочки положительной гауссовой кривизны прямоугольной в плане опертой на фермы
по контуру. Показано, что учет трещинообразования, пластических деформаций арматуры, а
также разносопротивляемости бетона имеет существенное влияние для расчета НДС
соответствующих конструкций.