Похожие презентации:
Formālas valodas. Neregulāras valodas
1. Formālas valodas Neregulāras valodas
© V. Vagale 2007-20092. Saturs
• Ievads• Baložu ligzdas princips (Dirihlē princips)
• Pumpējošā lemma
2
3.
{a b : n 0}n n
Neregulāras valodas
{vv : v {a, b}*}
R
Regulāras valodas
a *b
b*c a
b c ( a b) *
u.c.
3
4.
Kā mēs varam pierādīt, ka valoda L navregulāra?
Jāpierāda, ka neeksistē DFA, kas akceptē L.
Problēma: to nav tik vienkārši pierādīt.
Risinājums: Pumpējošā lemma !!!
4
5. Baložu ligzdas princips
56.
4 baloži3 baložu ligzdas
6
7.
Vienā baložu ligzdā būs 2 baloži7
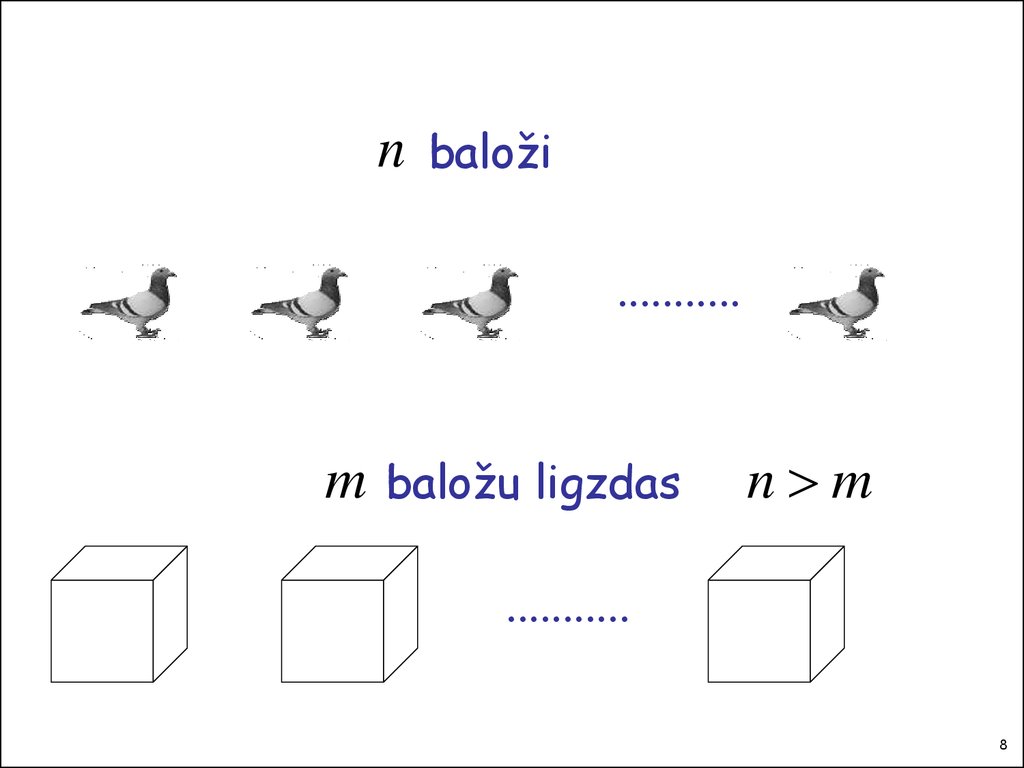
8.
nbaloži
...........
m
baložu ligzdas
n m
...........
8
9. Baložu ligzdas princips
nbaloži
m
baložu ligzdas
n m
Būs vismaz viena ligzda ar 2 baložiem
...........
9
10. Baložu ligzdas princips un DFA
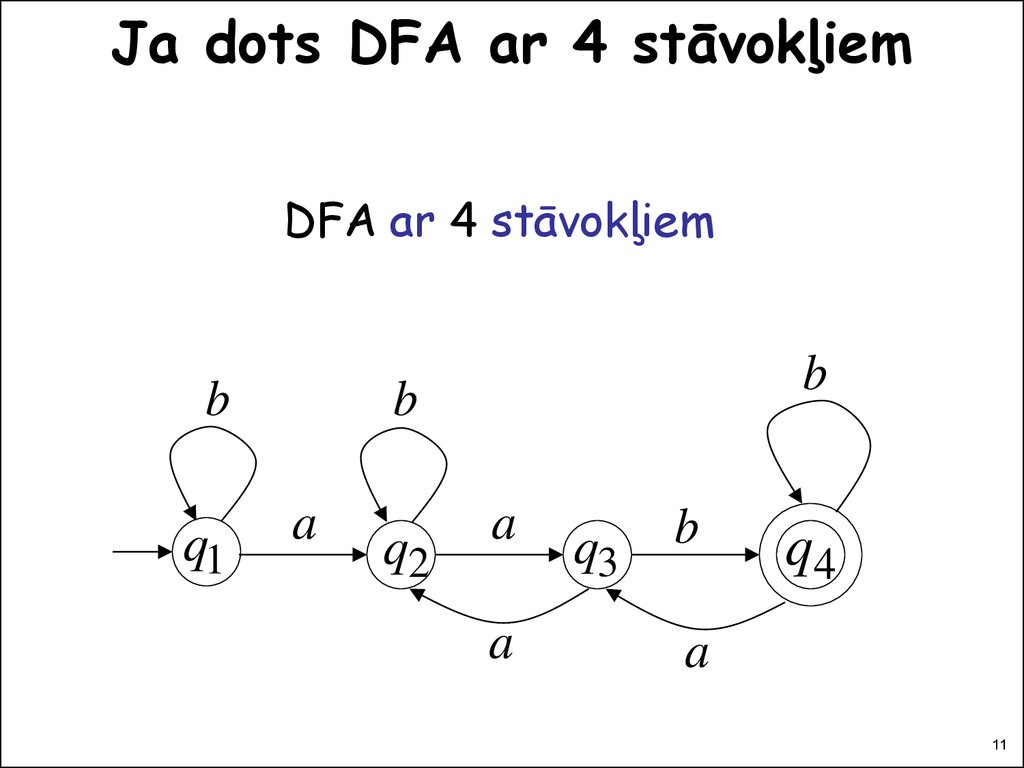
1011. Ja dots DFA ar 4 stāvokļiem
DFA ar 4 stāvokļiemb
q1
b
b
a
q2
a
a
q3
b
q4
a
11
12.
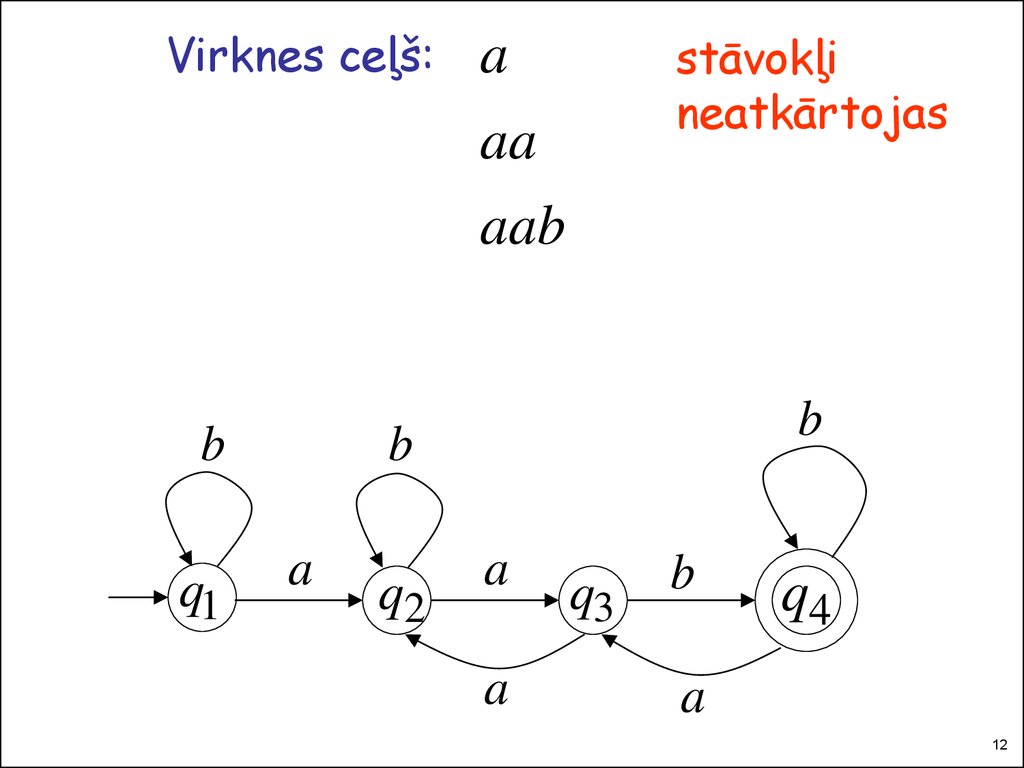
Virknes ceļš:b
q1
stāvokļi
neatkārtojas
a
aa
aab
b
b
a
q2
a
a
q3
b
q4
a
12
13.
Virknes ceļš:b
q1
b
a
q2
stāvokļi
aabb
atkārtojas
bbaa
abbabb
abbbabbabb... b
a
a
q3
b
q4
a
13
14.
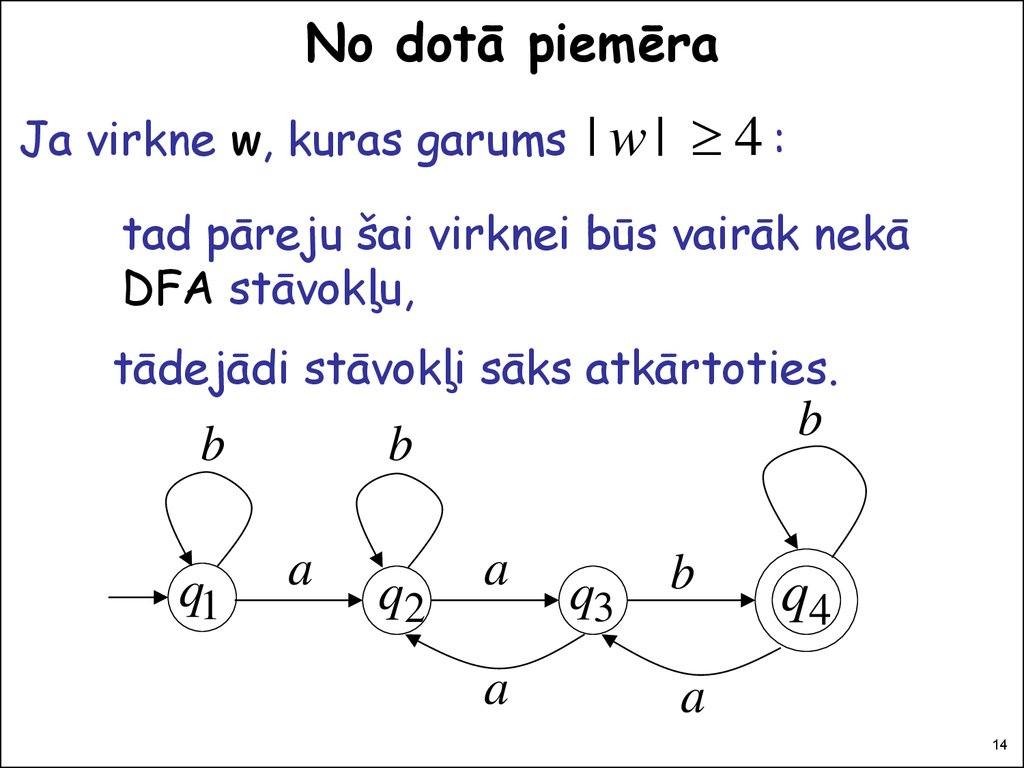
No dotā piemēraJa virkne w, kuras garums
| w| 4:
tad pāreju šai virknei būs vairāk nekā
DFA stāvokļu,
tādejādi stāvokļi sāks atkārtoties.
b
q1
b
b
a
q2
a
a
q3
b
q4
a
14
15.
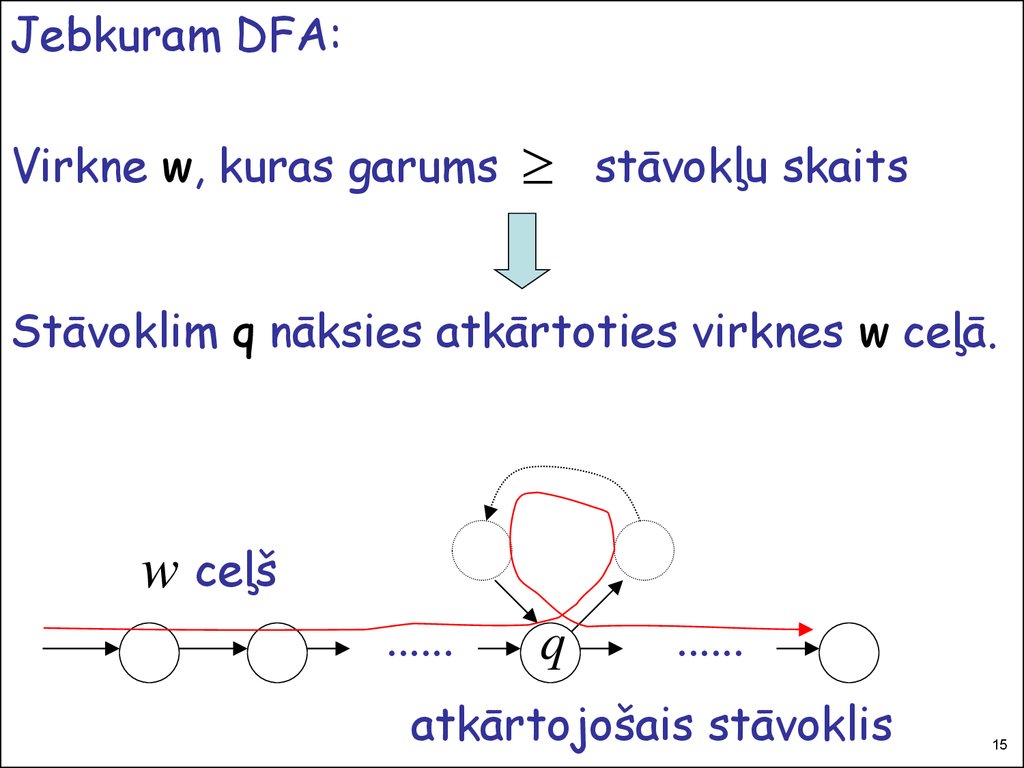
Jebkuram DFA:Virkne w, kuras garums
stāvokļu skaits
Stāvoklim q nāksies atkārtoties virknes w ceļā.
w ceļš
......
q
......
atkārtojošais stāvoklis
15
16.
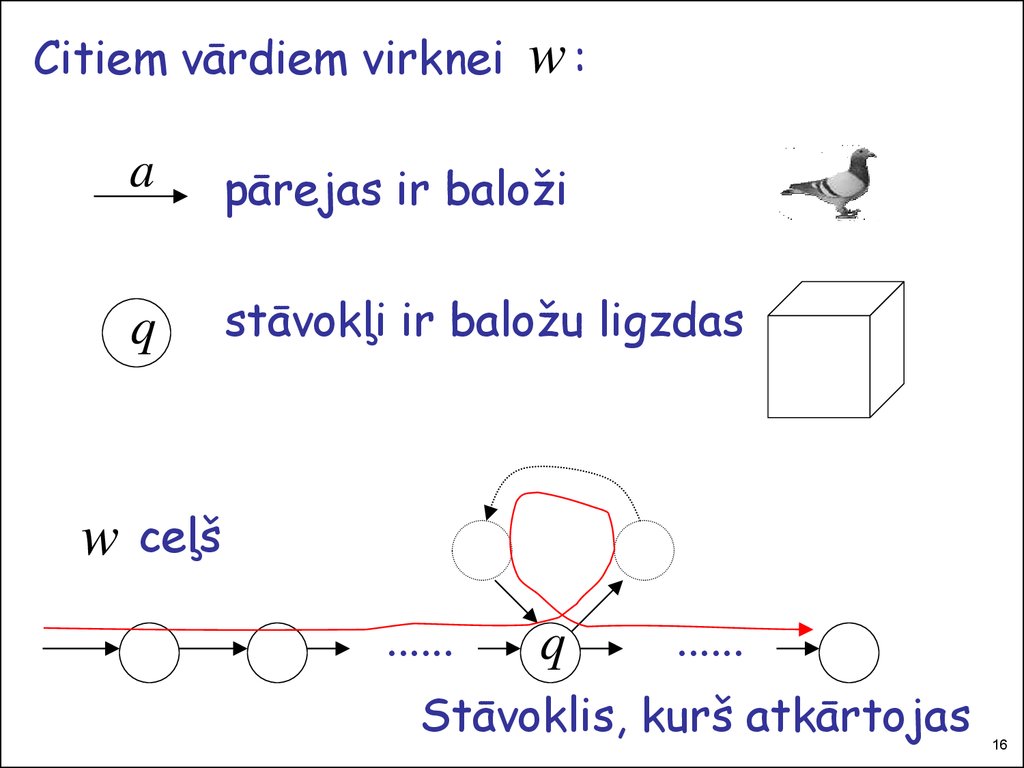
Citiem vārdiem virkneiw
w:
a
pārejas ir baloži
q
stāvokļi ir baložu ligzdas
ceļš
......
q
......
Stāvoklis, kurš atkārtojas
16
17. Pumpējošā lemma
1718.
Paņemsim neierobežotu valodu L.Eksistē DFA, kurš akceptē valodu L
m
stāvokļi
18
19.
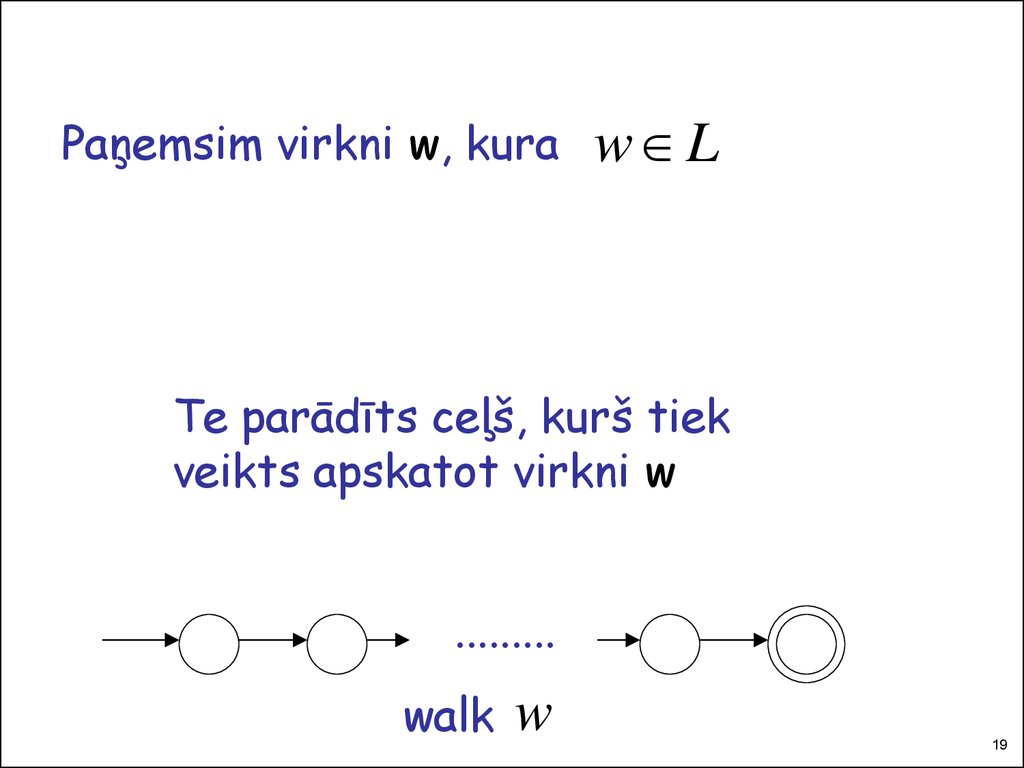
Paņemsim virkni w, kuraw L
Te parādīts ceļš, kurš tiek
veikts apskatot virkni w
.........
walk
w
19
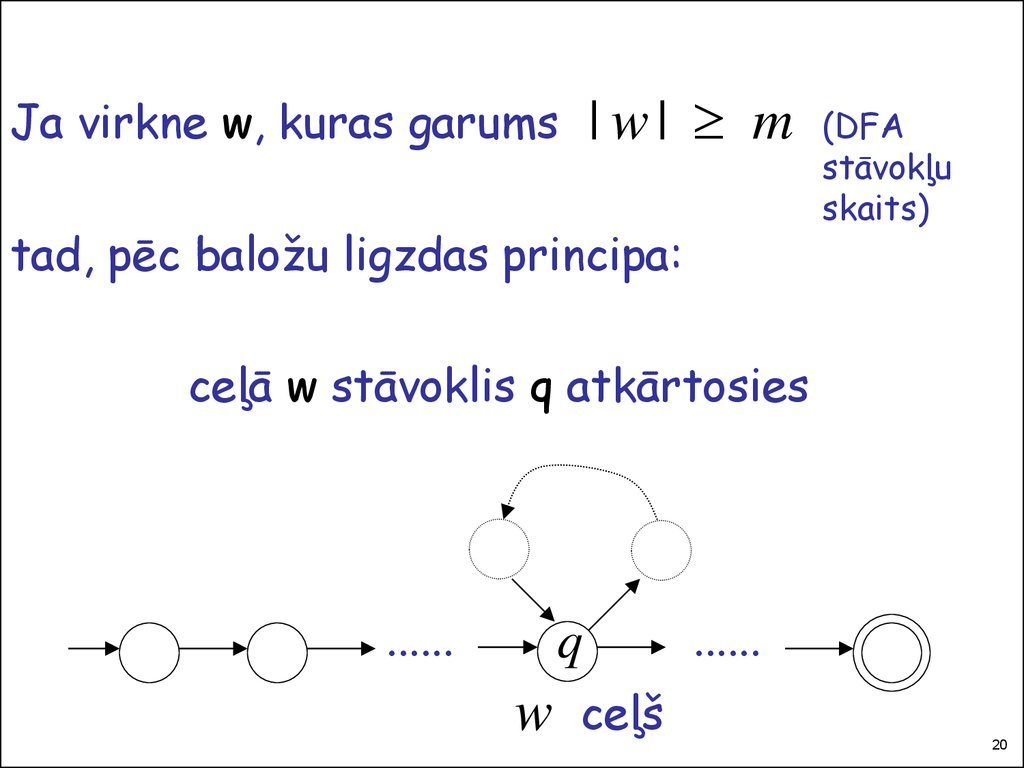
20.
| w| mJa virkne w, kuras garums
tad, pēc baložu ligzdas principa:
(DFA
stāvokļu
skaits)
ceļā w stāvoklis q atkārtosies
......
q
w
ceļš
......
20
21.
Pieņemsim, ka q ir pirmais stāvoklis, kuršsāk atkārtoties w ceļā
......
q
w ceļš
......
21
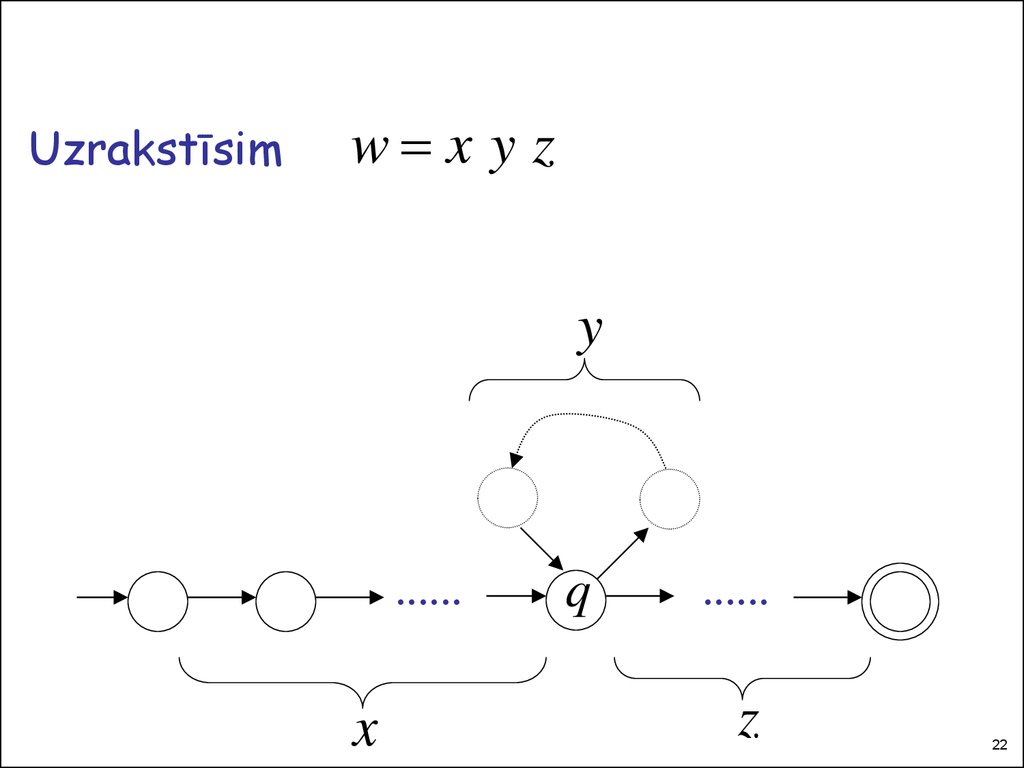
22.
Uzrakstīsimw x y z
y
......
x
q
......
z
22
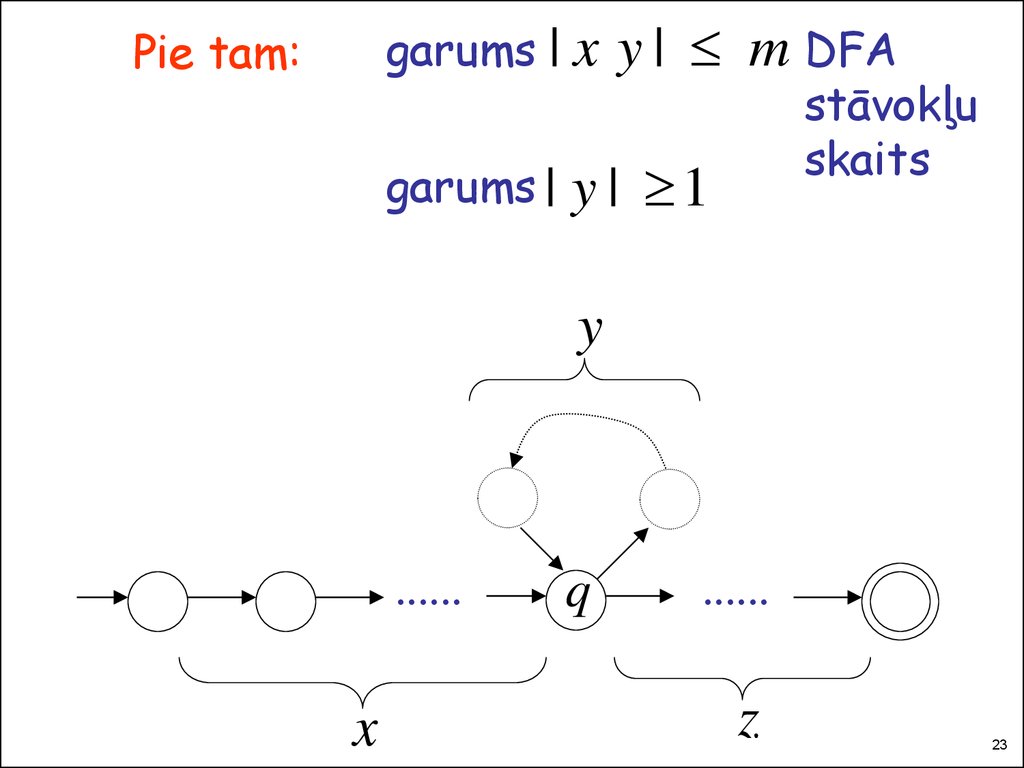
23.
garums | xPie tam:
garums |
y | m DFA
stāvokļu
skaits
y | 1
y
......
x
q
......
z
23
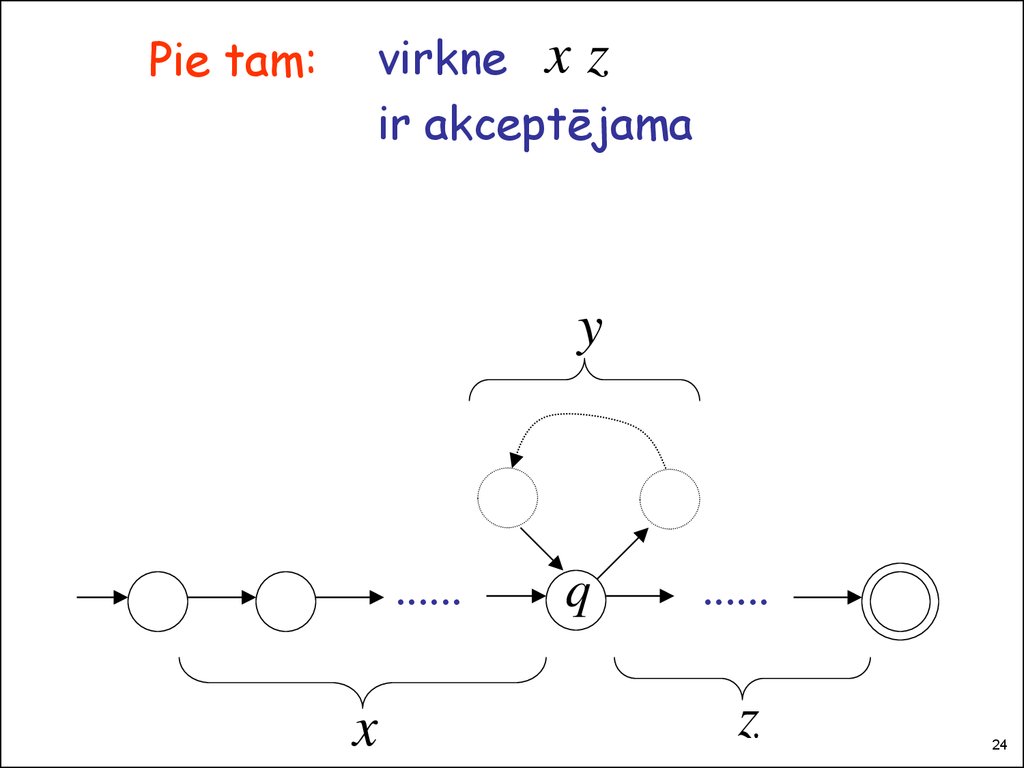
24.
Pie tam:virkne x z
ir akceptējama
y
......
x
q
......
z
24
25.
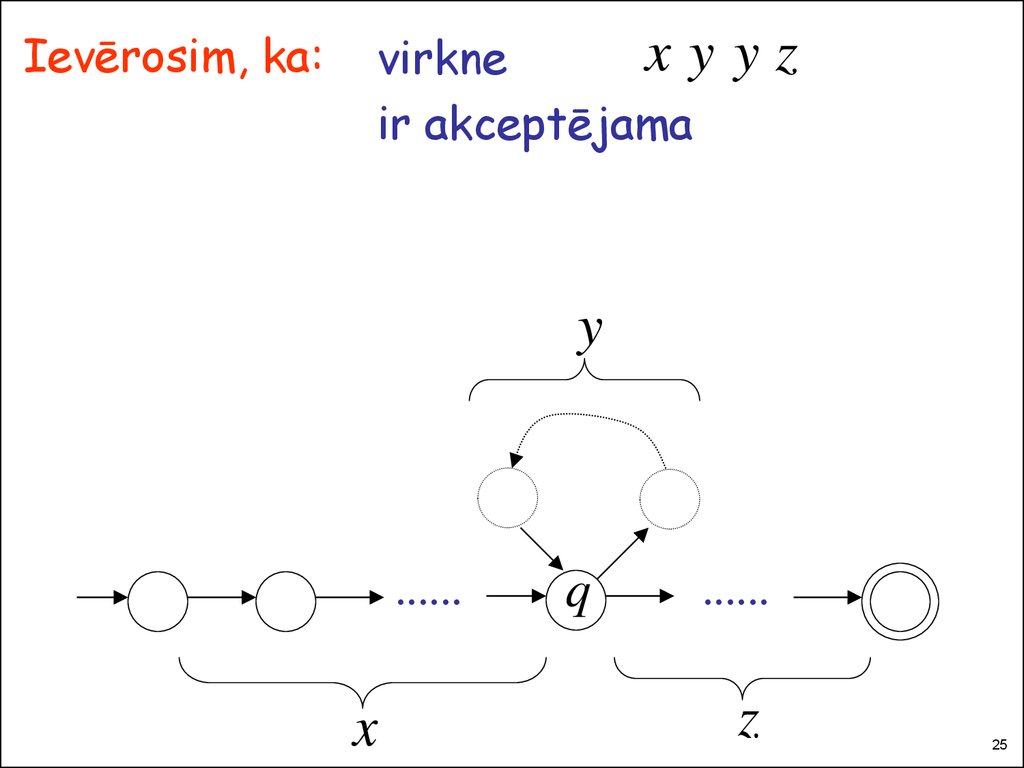
Ievērosim, ka:xy
virkne
ir akceptējama
yz
y
......
x
q
......
z
25
26.
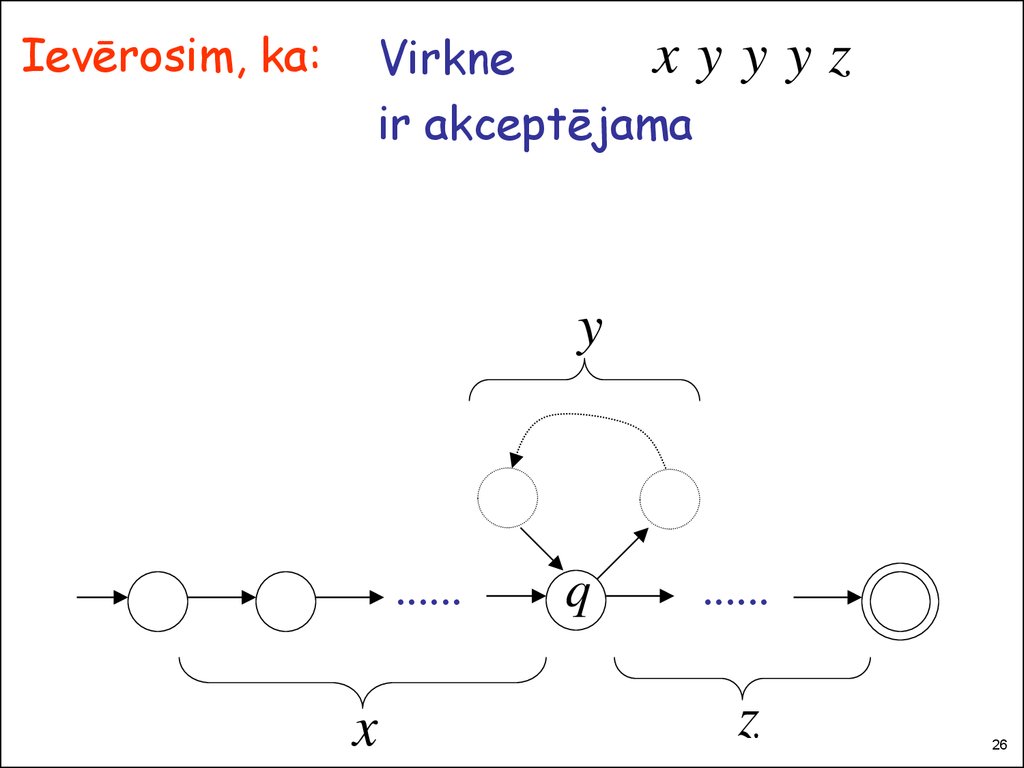
Ievērosim, ka:xy
Virkne
ir akceptējama
yyz
y
......
x
q
......
z
26
27.
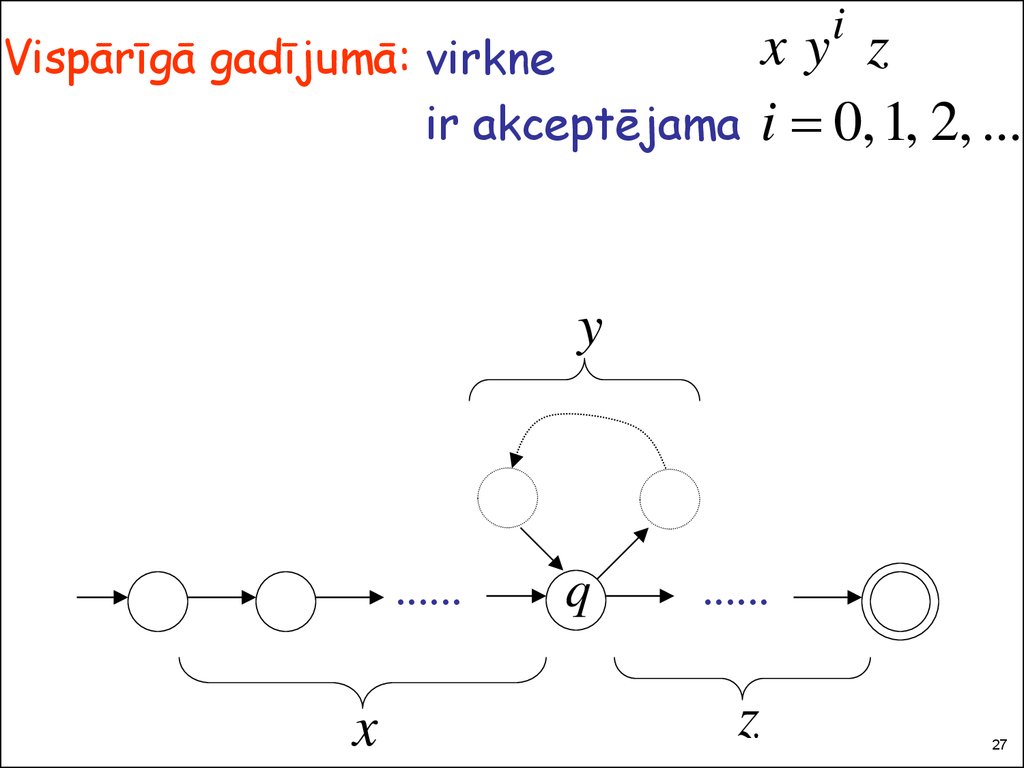
Vispārīgā gadījumā: virkneir akceptējama
i
xy z
i 0, 1, 2, ...
y
......
x
q
......
z
27
28.
Vispārīgā gadījumā:x y z L i 0, 1, 2, ...
i
Valoda, kuru akceptē DFA
y
......
x
q
......
z
28
29.
Citiem vārdiem, esam aprakstījuši:Pumpējošo lemmu !!!
29
30. Pumpējošā lemma
Ņemot neierobežotu regulāru valodu Leksistē konstante m, kurai
jebkurai virknei w L
mēs varam rakstīt
kur
ar garumu
w x y z
| x y | m un
tā ka:
xy z L
i
| w| m
| y | 1
i 0, 1, 2, ...
30
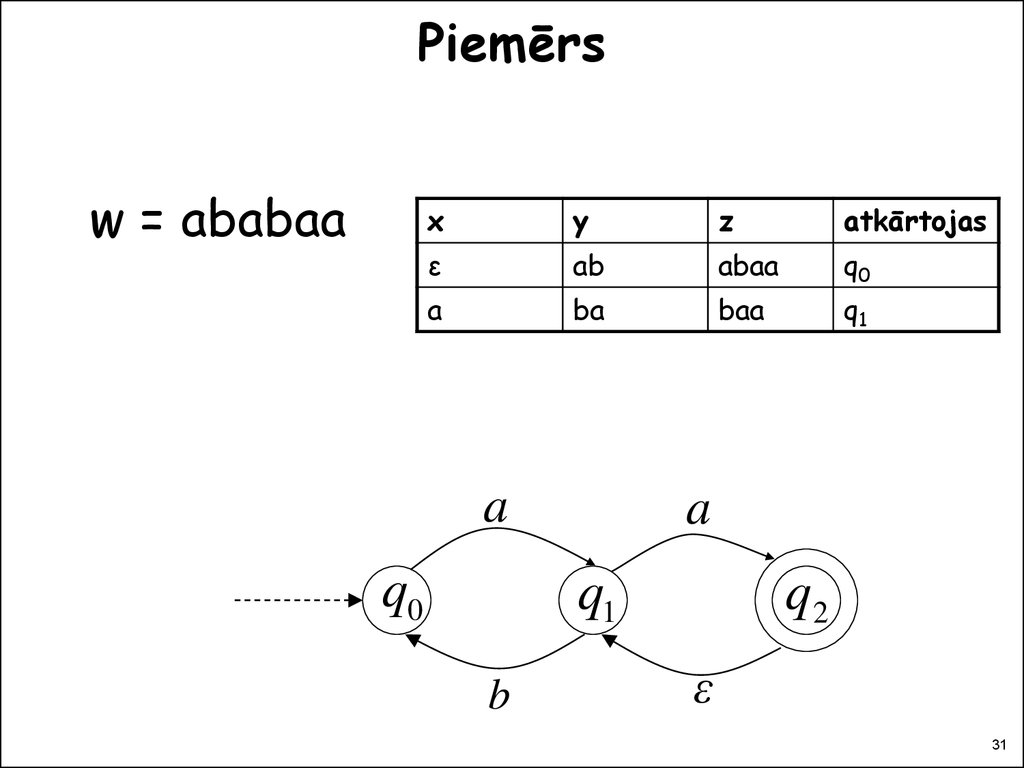
31. Piemērs
w = ababaax
y
z
atkārtojas
ε
ab
abaa
q0
a
ba
baa
q1
a
q0
a
q1
b
q2
ε
31
32. Pumpējošās lemmas izmantošana
3233.
Teorēma: ValodaL {a b : n 0}
n n
nav regulāra
Pierādījums: Izmanto Pumpējošo lemmu
33
34.
L {a b : n 0}n n
Pieņemsim pretējo, ka
L ir regulāra valoda
Tā kā L ir neierobežota
mēs varam izmantot Pumpējošo lemmu
34
35.
L {a b : n 0}n n
Pumpējošā lemmā m ir vesels skaitlis
Izvēlēsimies virkni w, tādu, ka
w L
garums
Pieņemsim
| w| m
w a b
m m
35
36.
Rakstām:a b xy z
m m
k
No Pumpējošās lemmas
izriet, ka
| x y | m, | y | 1
m
xy z a b
k
m m
a...aa...aa...ab...b
x
tādējādi:
m
z
y
x a ,y a , z a
i
j
m i j
b , j 1
m
36
37.
xy z Li
No Pumpējošās lemmas
i 0, 1, 2, ...
x a , y a , z a
i
j
xy z a (a ) a
0
i
j 0
m i j
m i j
b a
m
a
Pretruna!!!
b , j 1
m j
m j
m
b , j 1
m
b L
m
37
38.
w am 1 m 1
b
a. x a , y a , z a
i
b. x a
m 1 i
j
m i j 1 m 1
, y a b, z b
j
b
m 2
, j 0
, j 0
c. x a m 1 , y b, z b m 2
38
39.
a. k 0 xy0 z a i (a j ) 0 a m i j 1b m 1 a m j 1b m 1 , j 0b. k 2 xy2 z a m 1 i (a j b) 2 b m 2 a m 1 i 2 j b m , j 0
c. k 0 xy0 z a m 1b 0b m 2 a m 1b m 2
39
40.
Tādēļ:Slēdziens:
Mūsu pieņēmums, ka valoda L
ir regulāra ir nepareizs.
L Ir neregulāra valoda
40
41.
Neregulāras valodas{a b : n 0}
n n
Regulāras valodas
41
42. Uzdevumi
Pierādīt, ka valodas ir neregulāras:a. {vv | v {a, b}*}
R
b. {a b | n t}
c. {v | v {a, b}* un a ir mazāa nekā b}
n t
d . {a nbl c n l | n, l 0}
e. {a | n 0} n! 1 2 (n 1) n
n!
f . {x | x {a, b} un x x }
*
rev
g. {a | n 1}
n2
h. {a b | n t}
n t
i. {x | x {a, b} , and x x }
*
rev
42
43.
a. {vv | v {a, b}*}R
• Pieņemsim pretējo, ka šī valoda ir regulāra.
• Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina
Pumpējošās lemmas nosacījumus.
• Izvēlēsimies:
w a mbba m
xyz a mbba m , kur | xy | m un | y | 0 xyk z L, k 0
x a i , y a j , z a m i j bba m , kur j 0
xy0 z a i (a j ) 0 a m i j bba m a m j bba m
a m j bba m L
43
44.
b. {a b | n t}n t
• Pieņemsim pretējo, ka šī valoda ir regulāra.
• Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina
Pumpējošās lemmas nosacījumus.
• Izvēlēsimies:
w a m 1b m
xyz a m 1b m , kur | xy | m un | y | 0 xyk z L, k 0
K=0
44
45.
c. {v | v {a, b}*, kur a ir mazak nekā b• Pieņemsim pretējo, ka šī valoda ir regulāra.
• Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina
Pumpējošās lemmas nosacījumus.
• Izvēlēsimies:
w a mb m 1
xyz a mb m 1 , kur | xy | m un | y | 0 xyk z L, k 0
K=2
45





















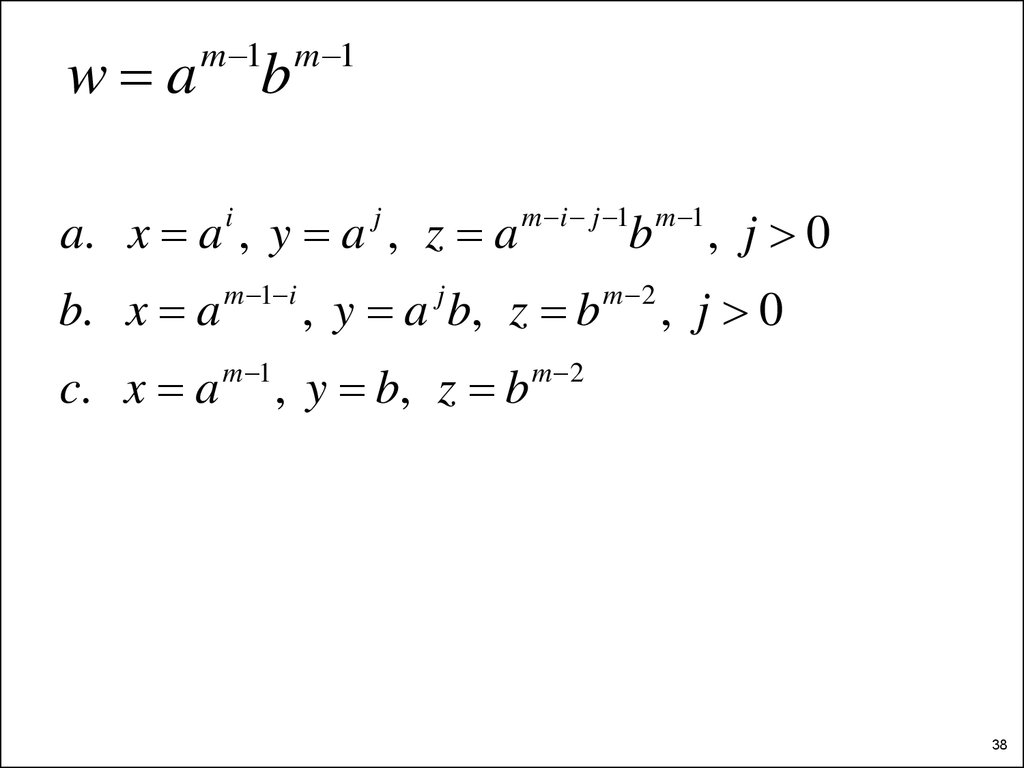
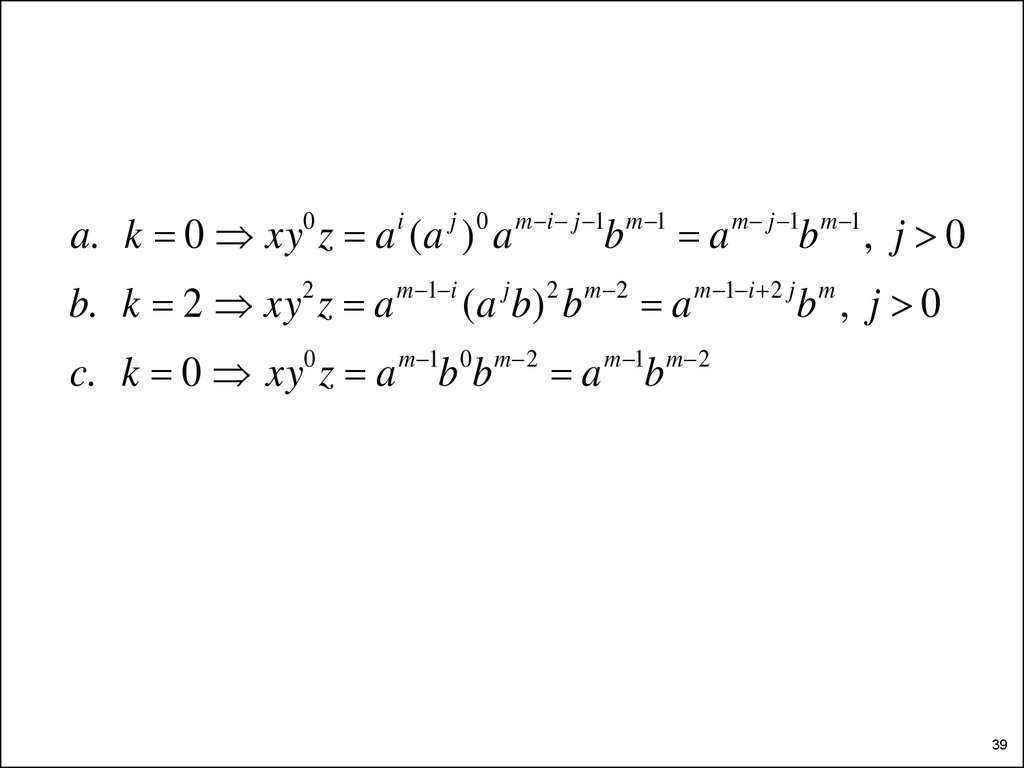






 Математика
Математика
