Экономические задачи. Задание 17, ЕГЭ

1.

2.

• 1 тип : Банковские задачи на кредиты
Дифференцированные платежи.
• 2 тип : Банковские задачи на кредиты
Аннуитетные платежи.
• 3 тип : Банковские задачи на вклады
Депозиты. Платежи разными суммами
• 4 тип : Заводские задачи на оптимизацию
• 5 тип : Фермерские и предпринимательские задачи

3.

Дифференцированный платеж - это платеж, когда сумма,
которую нужно выплачивать каждый месяц уменьшается,
потому что вы ежемесячно гасите одну и ту же часть основного
долга плюс ещё набежавшие проценты.
Уменьшение ежемесячного платежа
происходит за счет
уменьшения основного долга, так как процент начисляется на
меньшую сумму.
Таким образом наибольший платеж
приходится
на
первый
месяц
кредитования, а наименьший - на
последний.

4.

Год/
месяц
Долг
Начисленные %
Выплата
Основные обозначения:
а – кредит (иногда S);
n – платёжный период;
r – начисленные %, иногда целесообразнее перейти от десятичных
дробей к обыкновенным или ввести k=1+ r/100;
P – общая сумма выплат.

5.

Задача 1.
15 января планируется взять кредит в банке на 25 месяцев. Условия его
возврата таковы:
-1-го числа каждого месяца долг возрастает на r % по сравнению с концом
предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину
меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь
срок кредитования, на 13 % больше, чем сумма, взятая в кредит. Найдите r.
Из условия задачи следует, что каждый месяц долг уменьшался на
Введем переменные и заполним таблицу.

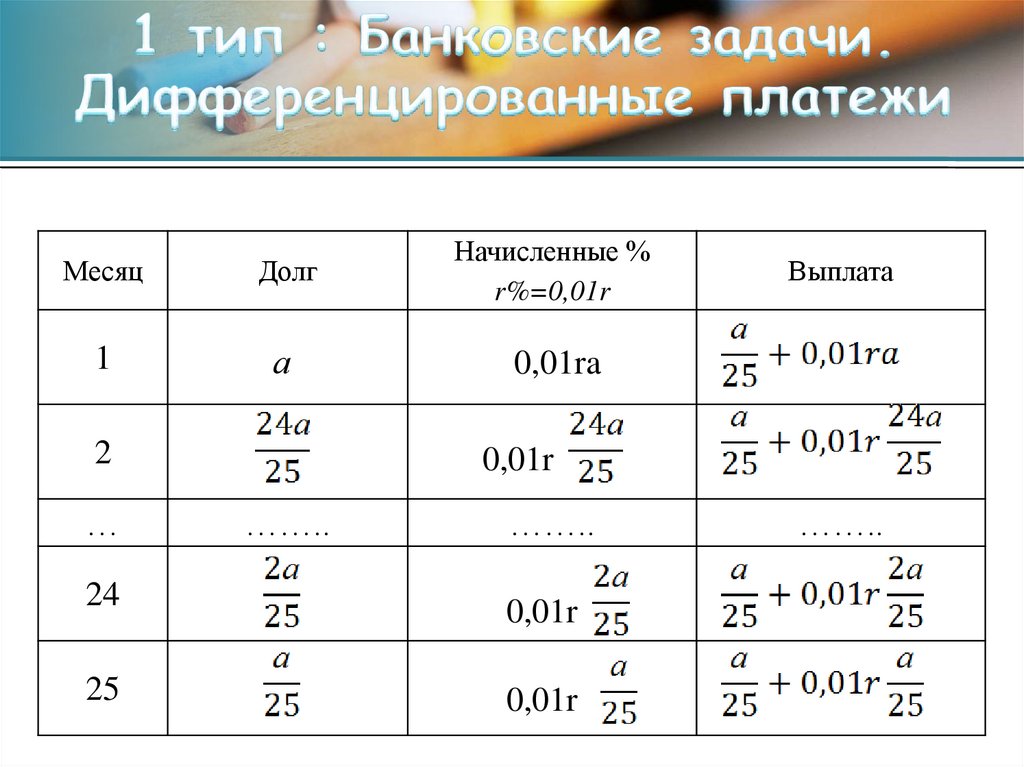
6.

Месяц
Долг
Начисленные %
r%=0,01r
1
а
0,01ra
2
…
24
25
Выплата
0,01r
……..
……..
0,01r
0,01r
……..

7.

1) Найдем полную выплату по таблице:
2) По условию полная выплата на 13 % больше, чем а.
Составим уравнение:
Ответ: 1%.

8.

Задача 2.
15 января планируется взять кредит в банке на 7 месяцев. Условия его
возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с
концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть
долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же
величину меньше долга на 15-е число предыдущего месяца.
Известно, что на четвёртый месяц кредитования нужно выплатить 54
тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока
кредитования?

9.

Месяц
1
Долг
Начисленные
%
2% = 0,02
а
0,02а
Выплата
2
…
….
….
……..
….
….
….
4
…
7

10.

1) Выплата на четвёртый месяц кредитования составляет 54000 рублей:
а=350000
2) Найдем полную выплату по таблице и подставим а:
Ответ: 378000 рублей.

11.

А3 ЕГЭ 2018. Основной срок.
15-го декабря планируется взять кредит в банке на 31 месяц. Условия
возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с
концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть
долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на 20
тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца кредит должен быть полностью
погашен.
Какой долг будет 15-ого числа 30-ого месяца, если общая сумма
выплат после полного его погашения составит 1348 тысяч рублей?
Заметим, что в данной задаче долг гасится равномерно до предпоследнего месяца, а
затем выплачивается весь остаток по кредиту. Это необходимо отразить в
таблице.

12.

Месяц
Долг
Начисленные
проценты, 0,01
Выплата, тыс руб
1
а
0,01а
20+0,01а
2
а-20
0,01(а-20)
20+0,01(а-20)
……..
…..
…….
……..
30
а-20*29
0.01(а-20*29)
20+0.01(а-20*29)
до 15ого числа 31
месяца
а-20*30
0.01(а-20*30)
1,01(а-20*30)
после 15ого числа
0

13.

Дифференцированный платеж с погашением
остатка долга в последний месяц
Найдем общую сумму выплат по таблице:
1) P =20+0,01a+20+0,01(a-20)+…+20+0,01(a-29*20)+1,01(a-30*20);
P = 600+0,2a-0,2(1+2+…+29)+1,01a-606;
P =1,31a – 6 – 87
2) По условию P=1348 тыс. руб., следовательно
1,31a=1441; a=1100 (тыс.руб)
2) Найдем долг на 15-е число 30 месяца.
(а-20*30) = 1100-600=500 (тыс.руб)
Ответ: 500000 рублей

14.

Дифференцированный платеж
с особыми условиями
Задача из сборника под редак цией Ф.Ф. Лысенко ЕГЭ - 2021 года.
Вариант 36.
1-ого марта 2020 года был взят кредит на 8 лет. Условия его возврата таковы:
- в апреле каждого года банк увеличивает сумму долга на 25%;
- с мая по август клиент должен выплатить часть долга;
- в сентябре каждого года с 1 -го по 6-й сумма долга должна быть на
одну и ту же величину меньше по сравнению с мартом;
- в сентябре 6-го года сумма долга должна равняться половине величины
кредита;
- в ноябре 7-го и 8-го годов сумма долга должна быть на одну и ту же
величину меньше, чем в ноябре предыдущего года.
На какую сумму был взят кредит, если первая выплата больше последней
на 9000 рублей?

15.

Дифференцированный платеж
с особыми условиями

16.

Дифференцированный платеж
с особыми условиями
По условию первая выплата больше последней на 9000 рублей.
Найдем эту разность по таблице:
S=432000 руб.
Ответ: 432000 рублей

17.

Дифференцированный платеж с
заданной таблицей
Математика, И.В. Ященко. 36 вариантов.
ЕГЭ 2021
15-го января Аркадий планирует взять кредит в банке на шесть месяцев в
размере 1 млн рублей. Условия его возврата следующие:
- 1-го числа каждого месяца долг увеличивается на r процентов по сравнению
с концом предыдущего месяца, где r — целое число;
- выплата должна производиться один раз в месяц со 2-го по 14-е число
каждого месяца;
-15-го числа каждого месяца долг должен составлять некоторую сумму в
соответствии со следующей таблицей.
Дата
Долг (в млн
рублей)
15.01 15.02 15.03 15.04 15.05 15.06 15.07
1
0,8
0,6
0,5
0,4
0,3
0
Найдите наименьшее значение r, при котором Аркадию в общей сумме
придётся выплатить больше 1,5 млн рублей.

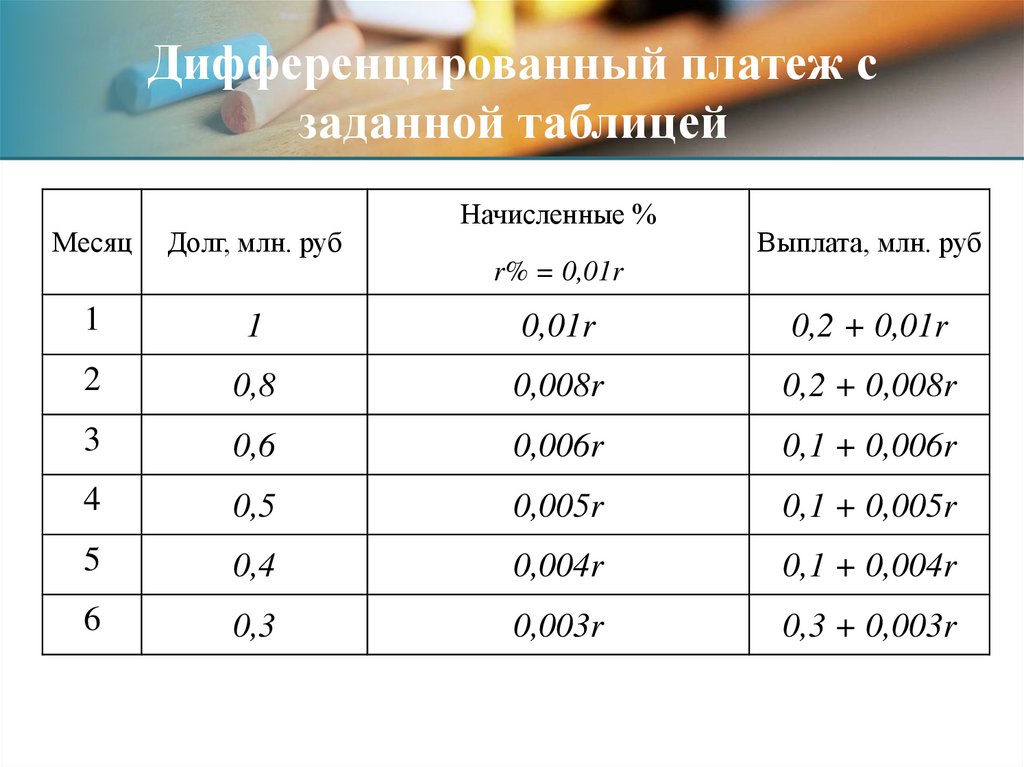
18.

Дифференцированный платеж с
заданной таблицей
Месяц
Долг, млн. руб
Начисленные %
Выплата, млн. руб
r% = 0,01r
1
1
0,01r
0,2 + 0,01r
2
0,8
0,008r
0,2 + 0,008r
3
0,6
0,006r
0,1 + 0,006r
4
0,5
0,005r
0,1 + 0,005r
5
0,4
0,004r
0,1 + 0,004r
6
0,3
0,003r
0,3 + 0,003r

19.

Дифференцированный платеж с
заданной таблицей
2) Полная выплата: 1+0,01r∙(1+0,8+0,6+0,5+0,4+0,3) = 1+0,036r
Найдем наименьшее значение r, при котором полная выплата
больше 1,5 млн рублей:
1+0,036r
1,5
r = 14%, так как r – наименьшее целое число
Ответ: 14%.

20.

Аннуитетный
платеж
это
гашение
кредита
равными суммами каждый месяц. Например, каждый месяц
выплата составляет 3000 рублей. В эту сумму входят
начисленные банком проценты и гашение основного долга так,
чтобы в результате получилась одна и та же сумма. В первую
очередь выплачиваются проценты, только затем снимают
основной долг, чтобы дополнить до определенной суммы.
Основной долг уменьшается неравномерно и медленно,
проценты набегают большие и поэтому такой кредит невыгоден.

21.

22.

23.

Задача 1.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит
под 10% годовых. Схема выплаты кредита следующая: 31 декабря
каждого следующего года банк начисляет проценты на оставшуюся
сумму долга (то есть увеличивает долг на 10%), затем Михаил
переводит в банк 2 928 200 рублей. Какую сумму взял Михаил в
банке, если он выплатил долг четырьмя равными платежами (то есть
за четыре года)?
Вид таблицы не меняется, а вот механизм выплат теперь иной. Выплаты
все одинаковые.

24.

1) Пусть х = 2 928 200 рублей – ежегодная выплата
Год
1
2
Долг
а
а + 0,1а –х=
=1,1а – х
Начисленные %
10% = 0,1
0,1а
0,1(1,1а –
х)
3
1,1(1,1а – х) – х =
=1,12а – 2,1х
0,1(1,12а – 2,1х)
4
1,1(1,12а – 2,1х) – х =
=1,13а – 3,31х
0,1(1,13а – 3,31х)
Выплата
х
х
х
х

25.

2) Долг выплатили за четыре года, то есть на начало пятого года
долг стал равен 0:
1,1(1,13а – 3,31х) – х =0
1,14а – 4,641х=0
Ответ: 9282000 рублей.

26.

Задача 2
31 декабря 2014 года Сергей взял в банке 8 420 000 рублей в кредит
под 10,5% годовых. Схема выплат кредита следующая – 31 декабря
каждого следующего года банк начисляет проценты на оставшуюся
сумму долга (то есть увеличивает долг на 10,5%), затем Сергей
переводит в банк x рублей. Какой должна быть сумма x, чтобы
Сергей выплатил долг двумя равными платежами (то есть за два
года)?

27.

1) Пусть а = 8 420 000 рублей – сумма, взятая в кредит
Год
Долг
Начисленные %
10,5% = 0,105
Выплата
1
а
0,105а
х
2
1,105а – х
0,105(1,105а – х)
х

28.

2) Долг выплатили за два года, то есть на начало третьего года долг
стал равен 0:
1,105(1,105а – х) – х=0
1,1052 а – 2,105х=0
Ответ: 4 884 100 рублей.

29.

Задача 1. Платежи разными суммами.
31 декабря 2014 года Антон взял в банке 1 млн рублей в кредит.
Схема выплаты кредита следующая: 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму
долга (то есть увеличивает долг на определенное количество
процентов), затем Антон переводит очередной транш. Антон
выплатит кредит за два транша, переведя первый раз 510 тыс.
рублей, во второй – 649 тыс. рублей. Под какой процент банк выдал
кредит Антону?

30.

Год
Долг, тыс.
1
а
Начисленные %
r%=0,01r
Выплата,
тыс.
0,01ra
510
2 а + 0,01ra – 510 0,01r (а + 0,01ra – 510)
649

31.

2) Долг выплатили за два года, то есть на начало третьего года
долг стал равен 0:
а + 0,01ra – 510 + 0,01r (а + 0,01ra – 510) – 649 = 0
r – 510 + 0,01r (а + 0,01ra – 510) – 649 = 0
r2 +149r – 1590 = 0
Ответ: r = 10%.

32.

Вклады под разные проценты.
Задача из сборника ЕГЭ 2021 под редакцией Ф.Ф. Лысенко. Вариант 32.
Ирина Евгеньевна хочет положить определённую сумму денег в банк под
проценты. Эту сумму она кладёт на вклад «А» с такими условиями:
первые два года банк начисляет q% годовых, третий и четвёртый годы р% годовых (проценты начисляются в конце года и добавляются к сумме
вклада ). Через 3 года сумма вклада (с учётом процентов) равна 290 400
рублей, а через четыре года - 348 480 рублей. Банк также предлагает
положить деньги на вклад «В» с такими условиями: первый год банк
начисляет q% годовых, второй и третий годы - р% годовых. Если бы
Ирина Евгеньевна изначально положила такую же сумму на вклад «В», то
через 3 года сумма вклада (с учётом добавленных процентов) была бы
равна 316 800 рублей. Чему была бы равна сумма вклада через четыре
года, если бы такую же сумму можно было разместить в банке под
наибольшее из q% и р% годовых число процентов?

33.

Вклады под разные проценты
Пусть S-сумма вклада; n=1+q/100; k=1+p/100
Вклад А. Sn2k2=348480 (1)
Sn2k=290400 (2)
Вклад В. Snk2=316800 (3)
1) Поделим (1) на (2) и найдем k: k=34848/29040=1,2; р=20%
2) Поделим (1) на (3) и найдем n: n=34848/31680=1,1; q=10%
3) Подставим n и k в (3) найдем S: S=200000 руб.
4) Sk4=200000*1,24 =414720 руб.
Ответ: 414720 руб.

34.

Вклады под разные проценты
Клиент планирует положить определенную сумму денег в
банки под некоторые проценты. Треть этой суммы он помещает
на вклад А под r% процентов годовых, а оставшуюся часть
денег на вклад Б под q% годовых (проценты начисляются в
конце года и добавляются к сумме вклада). Через год сумма
вкладов с учетом процентов увеличилась на 2/15 от
первоначального значения, а через два года стала составлять
463 200 рублей. Если бы клиент изначально положил бы 1/3
этой суммы на вклад Б, а оставшиеся средства — на вклад А, то
через год сумма вклад с учетом добавленных процентов)
увеличилась бы на 1/6 от первоначальной. Чему в этом случае
была бы равна сумма вкладов через два года?

35.

Вклады под разные проценты
Следовательно, при втором способе размещения денег через два года сумма
вкладов была бы равна:

36.

Основные обозначения: S – масса сплава
Вид задачи
Найти
1
Невзаимозаменяемые металлы
Наибольшее значение S
2
Взаимозаменяемые металлы
Наибольшее значение S

37.

Алюминий
Количество
рабочих, чел
1
2
Всего
Количество
металла за
смену, кг
Никель
Количество
рабочих, чел
Количество
металла за смену, кг

38.

Задача 1.
В двух шахтах добывают алюминий и никель. В первой шахте
имеется 20 рабочих, каждый из которых готов трудиться 5 часов в
день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг
никеля. Во второй шахте имеется 100 рабочих, каждый из которых
готов трудиться 5 часов в день. При этом один рабочий за час
добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд
промышленности производится сплав алюминия и никеля, в котором
на 2 кг алюминия приходится 1 кг никеля. При этом шахты
договариваются между собой вести добычу металлов так, чтобы
завод мог произвести наибольшее количество сплава. Сколько
килограммов сплава при таких условиях ежедневно сможет
произвести завод?

39.

Алюминий
Шахта 1
Шахта 2
Всего
Никель
Количество
Количество
Количество
металла за
рабочих, чел
рабочих, чел
смену, кг
Количество
металла за смену, кг
5∙1∙x=5х
5∙2∙(20 – х)=200–10 х
x
20 – х

40.

Алюминий
Никель
Кол-во
рабочих,
чел.
Кол-во
металла за
смену, кг
Кол-во
рабочих,
чел
Кол-во металла за смену,
кг
Шахта 1
x
5∙1∙x=5х
20 – х
5∙2∙(20 – х)=200–10 х
Шахта 2
y
5∙2∙у=10y
100 – у
5∙1∙ (100 – у) =500–5у
Всего

41.

Алюминий
Никель
Количество Количество
Количество
рабочих, металла за
рабочих, чел
чел
смену, кг
Количество
металла за смену, кг
Шахта 1
x
5∙1∙x=5х
20 – х
5∙2∙(20 – х)=200–10 х
Шахта 2
y
5∙2∙у=10y
100 – у
5∙1∙ (100 – у) )=500–5у
Всего
5x + 10y
200–10 х+500–5у =
= 700 – 10х – 5у
Так по условию Al : Ni = 2 : 1, то есть Al = 2Ni.
Тогда 5x + 10y = 2(700 – 10х – 5у). Выразим х.
х = 0,2(280-4y)

42.

Пусть S – масса сплава (Al+Ni), тогда
S = (5x + 10y) + (700 – 10х – 5у) =
= 700 – (280 – 4у) + 5у) = 420 + 9у
Рассмотрим функцию S(y) = 420 + 9у
Р
S наиб.= S (70)= 420 + 630 = 1050
Ответ: 1050 кг.

43.

Задача 2.
В двух областях есть по 100 рабочих, каждый из которых готов трудиться
по 10 часов в сутки на добыче алюминия или никеля. В первой области
один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во
второй области для добычи х кг алюминия в день требуется х2 человекочасов труда, а для добычи у кг никеля в день требуется у2 человеко-часов
труда.
Обе области поставляют добытый металл на завод, где для нужд
промышленности производится сплав алюминия и никеля, в котором на 1
кг алюминия приходится 1 кг никеля. При этом области договариваются
между собой вести добычу металлов так, чтобы завод мог произвести
наибольшее количество сплава. Сколько килограммов сплава при таких
условиях ежедневно сможет произвести завод?

44.

Алюминий
Никель
Количество
рабочих, чел
Количество
металла за
смену, кг
Количество
рабочих, чел
Количество
металла за смену, кг
1 обл.
x
10∙0,3∙x =3х
100 – х
10∙0,1∙(100 – х) = 100 – х
2 обл.
y
Всего
100 – у

45.

Алюминий
Количество Количество
рабочих,
металла за
чел
смену, кг
1 обл.
x
2 обл.
y
10∙0,3∙x =3х
Никель
Количество
рабочих, чел
Количество
металла за смену, кг
100 – х
10∙0,1∙(100 – х) = 100 – х
100 – у
Всего
2) Так по условию Al : Ni = 1 : 1, то есть Al = Ni.
Тогда

46.

3) Пусть S – масса сплава (Al+Ni), тогда
S=
S=
Рассмотрим функцию S
Р
S наиб.= S (10)= 150+45 + 5 = 200
Ответ: 200 кг.

47.

Вариант 3.
В двух областях есть по 160 рабочих, каждый из которых готов
трудиться по 5 часов в сутки на добыче алюминия или никеля. В
первой области один рабочий за час добывает 0,1 кг алюминия или
0,3 кг никеля. Во второй области для добычи х кг алюминия в день
требуется х2 человеко-часов труда, а для добычи у кг никеля в день
требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий,
или никель, причём 1 кг алюминия можно заменить 1 кг никеля.
Какую наибольшую массу металлов можно добыть в двух областях
суммарно для нужд промышленности?

48.

Алюминий
1 обл.
2 обл.
Всего
Никель
Количество
рабочих, чел
Количество
металла за
смену, кг
Количество
рабочих, чел
Количество
металла за смену, кг
---
---
160
5∙0,3∙160=240

49.

Алюминий
Никель
Количество
рабочих, чел
Количество
металла за
смену, кг
Количество
рабочих, чел
Количество
металла за смену, кг
1 обл.
---
---
160
5∙0,3∙160=240
2 обл.
х
=
Всего
160-х

50.

Алюминий
Никель
Количество
рабочих, чел
Количество
металла за
смену, кг
Количество
рабочих, чел
Количество
металла за смену, кг
1 обл.
---
---
160
5∙0,3∙160=240
2 обл.
х
=
160-х
Всего
2) Пусть S – масса сплава (Al+Ni), тогда
240+

51.

S наиб.= S (80)= 20+240 + 20 = 280
Ответ: 280 кг.

52.

Задача 1.
У фермера есть два поля, каждое площадью 10 гектаров. На
каждом поле можно выращивать картофель и свёклу, поля можно
делить между этими культурами в любой пропорции.
Урожайность картофеля на первом поле составляет 400 ц/га, а на
втором — 300 ц/га. Урожайность свёклы на первом поле
составляет 300 ц/га, а на втором — 400 ц/га.
Фермер может продавать картофель по цене 10 000 руб. за
центнер, а свёклу — по цене 11000 руб. за центнер. Какой
наибольший доход может получить фермер?

53.

Картофель
Площадь поля, га
1 поле
2 поле
Урожай, ц
Свекла
Площадь поля, га
Урожай, ц

54.

Картофель
Площадь поля, га
1 поле
2 поле
х
у
Свекла
Урожай
400х
300у
Площадь поля, га
10-х
10-у
Урожай
300(10-х)=
3000-300х
400(10-у)=
4000-400у

55.

1) Пусть S1 – доход с первого поля (тыс. руб.), тогда
S1=10∙400х+11∙(3000-300х)
S1=700х+33000, возрастающая функция, наиб. значение достигает
при набольшем х: S1 наиб.=S1(10)=40000
2) Пусть S2 – доход со второго поля, тогда
S2=10∙300у+11∙(4000-400у)
S2=-1400у+44000, убывающая функция, наиб. значение достигает
при наим. у: S2 наиб.=S2(0)=44000
3) Пусть S – наибольший общий доход, тогда
S= S1 наиб.+ S2 наиб.=84 000 (тыс.руб.)
Примечание.
Данную задачу можно решить арифметически, с письменным
обоснованием на каком поле какую культуру выгоднее выращивать
Ответ: 84 000 000 руб.

56.

л

57.

58.

59.

60.

61.

62.

63.

64.

Спасибо за внимание!