Течение воды через песок и трубки

1. Лекция 1. Течение воды через песок и трубки.

Владимир Павлович Крайнов,
кафедра теоретической физики
МФТИ, 03.09.2016

2.

• Характерный размер песчинки равен а;
пористость песка равна (это
отношение объема пустот к суммарному
объему песчинок и пустот). Медленное
течение воды (или нефти) через поры в
песке или другой пористой среды под
действием градиента давления – это
вязкое течение Пуазейля, имеющее
место при малых числах Рейнольдса.

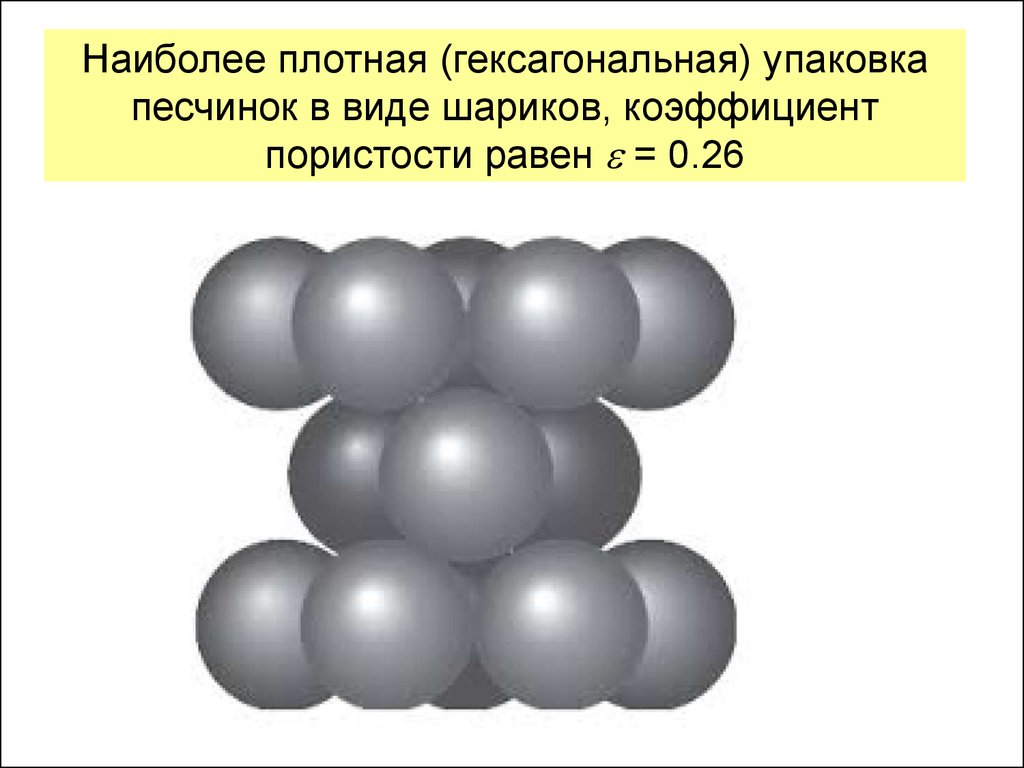
3. Наиболее плотная (гексагональная) упаковка песчинок в виде шариков, коэффициент пористости равен  = 0.26

Наиболее плотная (гексагональная) упаковка
песчинок в виде шариков, коэффициент
пористости равен = 0.26

4.

• Мы моделируем поры полыми
трубочками. Пусть l – длина трубочки, r
– ее характерный поперечный размер, а
р- малая разность давлений на концах
трубочки. Скорость медленного течения
пропорциональна градиенту давления :
это первый член разложения скорости в
ряд Тейлора в уравнениях НавьеСтокса. Подчеркнем, что скорость
течения определяется именно
градиентом давления, а не разностью
давлений на концах трубочки.

5.

• Коэффициент пропорциональности в
этой зависимости (уже не содержащий
l) можно оценить из соображений
размерности – он содержит плотность
воды , r и кинематическую вязкость
воды . Последняя величина имеет
размерность см2/с – она оценивается
как произведение скорости молекулы
воды на длину ее свободного пробега
(вязкость среды определяется
передачей импульса от одной молекулы
к другой при столкновении друг с
другом).

6.

• Получаем качественно формулу
Пуазейля
• (1)
p r2 г
см2
см
u
=
2 2
3
2
l см с (г/см )(см /с) с
• Объемный расход жидкости через одну
трубочку оценивается как
• (2)
4
p r
q ur
l
2

7.

• Если трубочка имеет цилиндрическую форму
радиуса r, то численный коэффициент в этой
зависимости равен /8 (формула Пуазейля).
Мы видим, что коэффициент имеет порядок
единицы. Этот факт является достаточно
общим утверждением: решение
дифференциального уравнения (в данном
случае, уравнения Навье-Стокса) с
коэффициентами порядка единицы, как
правило, также имеет порядок единицы. Эти
соотношения справедливы при малом
значении безразмерного числа Рейнольдса
Re
ur
1.
• Тогда можно пренебречь нелинейным
слагаемым в уравнении Навье-Стокса.

8.

• Рассмотрим параллелепипед из песка
длиной l и поперечным сечением S.
Скорость течения воды через этот
параллелепипед запишем в виде,
аналогичным формуле (1)
p k
u
l
• Величина k называется
коэффициентом проницаемости. Он
имеет размерность площади. Нам
требуется оценить его величину.

9.

• Объемный расход воды через весь
параллелепипед равен (закон Дарси)
p kS
• (3)
Q
l
• Это верно, если считать, что вода течет
через множество трубочек, причем
течения через различные трубочки не
зависят друг от друга (лучше сказать, в
лабиринте пустот в песке они редко
пересекаются). Радиус трубочки r
оценим ниже.

10.

• В такой модели пористость
(отношение объема пустот к
суммарному объему песчинок и пустот)
можно представить в виде
2
• (4)
V ' S 'l n ' r l
.
V
Sl
V
• Здесь S ' n ' r 2 - суммарная площадь
трубочек, через которые просачивается
вода. Величина это число трубочек.
Числовые множители во всех оценках
опускаем.

11.

• Число песчинок оценивается как
• (5)
V V ' 1 V
n
a
3
a
3
.
• Площадь поверхности всех песчинок,
2
которые омывает вода, равна a n .
• Главная идея модели состоит в том,
что, с другой стороны, эта площадь
равна площади поверхности всех
пустотелых трубочек, которые омывает
вода. Получаем:

12.

• (6)
a n n ' rl
• Подставляя (4) и (5) в (6), находим
1 V V
a
r
• Отсюда получаем оценку для радиуса
каждой трубочки
• (7)
2
r
1
a.

13.

• Конечно, при малой проницаемости
( << 1) радиус трубочки мал по
сравнению с размером песчинки, в
соответствии с качественным
представлением о просачивании.
Далее, из-за изгибов трубочки при
обтекании песчинки длина трубочки
больше высоты параллелепипеда l. Для
шарообразной песчинки радиуса а эта
длина увеличивается в /2 раз. Однако
при качественном подходе мы
пренебрегаем всеми такими факторами.

14.

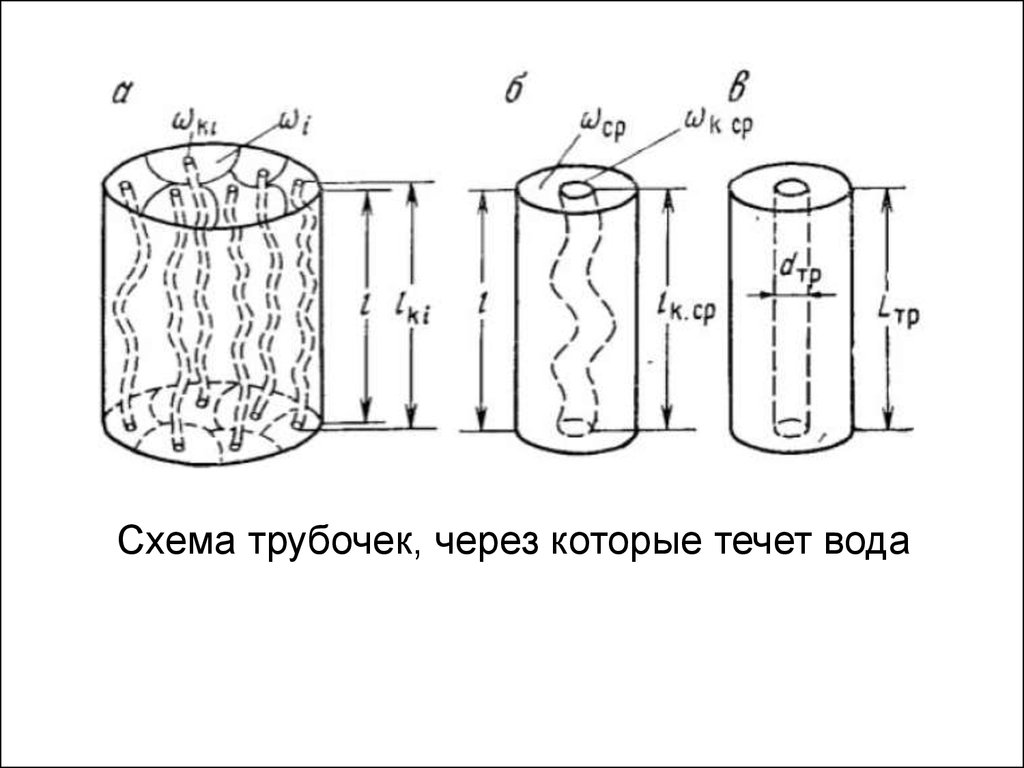
Схема трубочек, через которые течет вода

15.

• Объемный расход q воды через одну
трубочку дается соотношением (2).
Расход воды через все трубочки равен
p r
Q qn '
n'
l
4
• Сравнивая эту формулу с
определением (3), находим
коэффициент проницаемости (учитывая
(4))
4
2
n'r
S 'r
k
r 2.
S
S

16.

• Подставляя радиус трубочки (7) в это
соотношение, получим
3
• (8)
k
1
2
2
a .
• Она справедлива при малом значении
числа Рейнольдса
ua
Re
1.
1

17.

• При обычном условии << 1 выражение
(8) приобретает совсем простой вид
3 2
• (9)
k a .
• Видно, что коэффициент
проницаемости очень сильно зависит от
пористости среды.
• Если учесть все численные множители,
опущенные выше, а также увеличение
длины трубочки из-за ее изгиба при
обтекании песчинок, о котором
упоминалось выше, то получим
формулу Козени-Кармана

18. Формула Козени-Кармана

• Она хорошо согласуется с
экспериментальными данными.
• (10)
3
k
45 1
2
2
a .
Малый численный множитель связан с
увеличением длины трубочек из-за их
сильного искривления.

19. Водяные часы

• Сначала определим форму водяных
часов, пренебрегая трением.
• Скорость вытекающей
• воды через отверстие
• радиуса r должна быть
• постоянна, чтобы часы
• шли равномерно.
• Обозначим ее V0.

20.

• Обозначим радиальную координату
стенок часов x, а высоту стенок для
этой координаты y(x).
• Уравнение несжимаемости воды имеет
2
2
вид
r V x V ( x).
0
• Здесь V ( x ) - скорость воды для
координаты x.
• Уравнение Бернулли для жидкости без
трения имеет вид 1
1 2
2
V0 gy V x
• (закон сохранения
2
2
• энергии)

21.

• Исключая из этих двух уравнений скорость
V ( x ) , находим уравнение формы часов
V02 r 4
y ( x)
1 4 ; y x r 0.
2g x
• Обозначим высоту сосуда H y x
• Тогда уравнение формы водяных часов
принимает вид
r4
V02
y ( x) H 1 4 ; H
.
2g
x

22.

• Начальный объем воды в часах равен
H
x 2 dy 2 r 2 H .
0
• Вся вода вытечет за время Т,
определяемое из соотношения
r V0T .
2
• Получаем
H
T
2g
• Время вытекания не зависит от размера
отверстия сосуда! Для высоты Н = 20м
• получим Т = 1 с.

23. Учет трения в часах

• Возьмем сосуд в форме цилиндра, из
которого по узкой трубке вытекает вода
• Радиус узкой трубки обозначим через r0

24. Уравнение Навье-Стокса

• Стационарное уравнение Навье-Стокса
при малых числах Рейнольдса имеет вид
V p.
• Здесь - коэффициент кинематической
вязкости. В цилиндрических координатах
имеем для трубочки длиной l
d 2V 1 dV
p
.
2
dr
r dr
l

25.

• Решение уравнения Навье-Стокса,
обращающееся в нуль на стенке
трубочки радиуса r0 имеет вид
p 2 2
V (r )
r0 r
4
• Скорость распределена по сечению
трубочки по параболическому закону.
• Масса жидкости, протекающая в 1 с
через трубочку, равна
r0
Q 2 V (r )rdr.
0

26.

• Вычисляя интеграл, получим формулу
Пуазейля для массы, вытекающей в единицу
времени из узкой трубки длиной l, равна
p 4
Q
r0
8 l
• Здесь - коэффициент кинематической
вязкости, а р = gl – перепад давления в
узкой трубке. Итак, расход жидкости равен
g 4
Q
r0
8

27.

• Вся вода вытечет из сосуда за время Т,
определяемое из соотношения
QT R H
2
• Здесь Н – высота основного сосуда, а R
- его радиус. Получаем
8 R 2 H
T
4
0
gr
.
• Кинематическая вязкость воды равна
• = 0.01 см2/с. Возьмем r0 = 1 мм, R = 10
cм, Н = 1 м. Получаем Т = 2.2 часа.

28.

• Если вместо воды в тот же сосуд налить
глицерин, то из-за его большой вязкости
= 6.8 см2/с, время работы часов
значительно увеличивается: до 2
месяцев.
• Однако отверстие сосуда нельзя делать
слишком малым из-за поверхностного
натяжения жидкости, которое может
прекратить ее истечение.

29.

В древние времена
промежуток времени
измерялся количеством
воды, вытекавшей
капля за каплей
из малого отверстия,
сделанного на дне сосуда.
Здесь время вытекания
определяется другой физикой:
поверхностным натяжением
воды, т.е. временем
образования очередной
капли.

30. Спасибо за внимание