Логические основы работы компьютера

1. Логические основы работы компьютера.

1

2. Логика - наука, изучающая законы и формы мышления. Этапы развития логики: I этап - формальная логика. Основатель — Аристотель

(384-322 гг. до
н.э.), ввел основные формы абстрактного мышления.
II этап - математическая логика. Основатель - немецкий ученый и
философ Лейбниц (1642-1716), предпринял попытку логических
вычислений.
III этап - математическая логика (булева алгебра). Основатель английский математик Джордж Буль (1815-1864), ввел алфавит,
орфографию и грамматику для математической логики.
3

3. Алгебра логики - это математический аппарат с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают

логические высказывания.
Высказывание (суждение) - повествовательное предложение,
о котором можно сказать, истинно оно или ложно.
Высказывание может принимать только одно из двух логических
значений - истинно (1) или ложь (0).
Примеры высказывании:
• Земля - планета Солнечной системы (истинное высказывание).
3 + 6 > 10 (ложное высказывание).
4

4. Утверждение — суждение, которое требуется доказать или опровергнуть, например, сумма внутренних углов треугольника равна180°.

Рассуждение — цепочка высказываний или утверждений,
определённым образом связанных друг с другом, например, если
хотите начать работать на компьютере, то необходимо сначала
включить электропитание.
Умозаключение — логическая операция, в результате которой из
одного или нескольких данных суждений получается (выводится)
новое суждение.
Область знаний, которая изучает истинность или ложность
высказываний (суждений), называется математической логикой.
Утверждения в математической логике называются
логическими выражениями.
5

5. Высказывания бывают простые и сложные.

• Простое высказывание (логическая
переменная)
содержит только одну простую мысль. Логические
переменные обычно обозначаются буквами латинского
алфавита : A, В, С, D...
Например, А = {Квадрат - это ромб}.
• Сложное высказывание (логическая
функция)
содержит несколько простых мыслей, соединенных между
собой с помощью логических операций.
Например,
F(A,B) = {Лил дождь, (и) дул холодный ветер}.
А
В
7

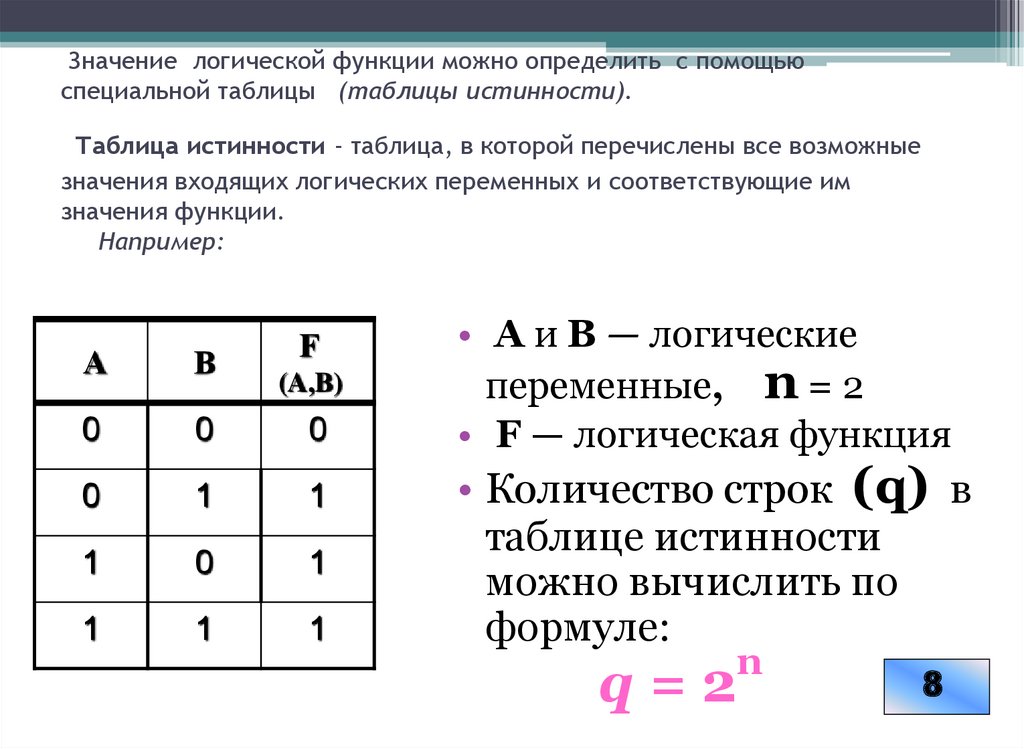
6. Значение логической функции можно определить с помощью специальной таблицы (таблицы истинности). Таблица истинности - таблица,

в которой перечислены все возможные
значения входящих логических переменных и соответствующие им
значения функции.
Например:
F
А
В
0
0
0
0
1
1
1
0
1
1
1
1
(A,B)
• А и В — логические
переменные, n = 2
• F — логическая функция
• Количество строк (q) в
таблице истинности
можно вычислить по
формуле:
q=2
n
8

7. Логический элемент (вентиль) – часть электронной логической схемы, которая выполняет элементарную логическую операцию. Каждый

логический элемент имеет свое условное
обозначение, имеет один или несколько входов,
на которые подаются сигналы «высокого»
напряжения («1») и «низкого» напряжения («0»),
и только один выход.
9

8. Основные логические операции

1. Отрицание (инверсия),
соответствует частице НЕ, словосочетанию
НЕВЕРНО, ЧТО;
• обозначение: А
таблица истинности
А
0
1
А
1
0
Инверсия логической переменной
истинна, если сама переменная ложна,
и, наоборот, инверсия ложна,
если переменная истинна, пример:
А={На улице идет снег}. A={Неверно, что на улице идет снег}
А={На улице не идет снег};
10

9. Логическое сложение (дизъюнкция), от лат. disjunctio - различаю: • соответствует союзу ИЛИ; • обозначение: +, V; • таблица

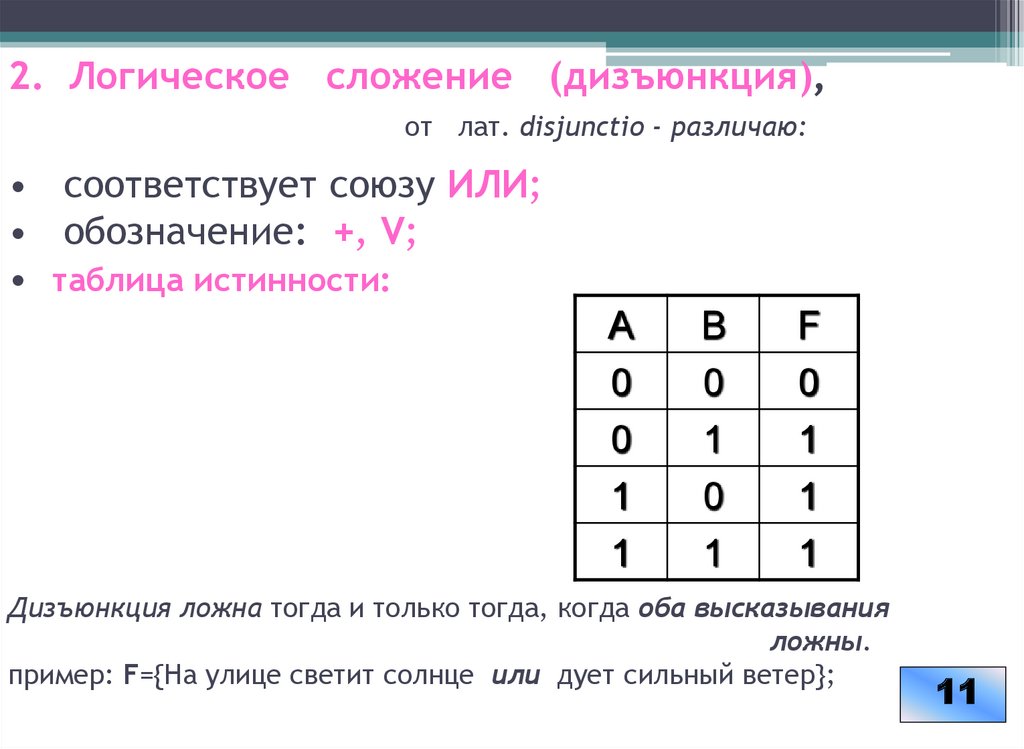
2. Логическое сложение (дизъюнкция),
от лат. disjunctio - различаю:
• соответствует союзу ИЛИ;
• обозначение: +, V;
• таблица истинности:
A
0
0
1
1
B
0
1
0
1
F
0
1
1
1
Дизъюнкция ложна тогда и только тогда, когда оба высказывания
ложны.
пример: F={Ha улице светит солнце или дует сильный ветер};
11

10. 3. Логическое умножение (конъюнкция), от лат. conjunctio - связываю: • соответствует союзу И (в естественном языке: и А, и В

как А, так и В
А вместе с В
А, несмотря на В
А, в то время как В);
обозначение:
*, ^;
таблица истинности:
Конъюнкция истинна тогда и
только тогда, когда оба
высказывания истинны.
пример:
F={Ha улице светит солнце и дует сильный ветер};
A
0
0
1
1
B
0
1
0
1
F
0
0
0
1
12

11. Любое сложное высказывание можно записать с помощью основных логических операций И, ИЛИ, НЕ. С помощью логических схем И, ИЛИ,

НЕ
можно реализовать любую
логическую функцию,
описывающую работу различных
устройств компьютера.
13

12. Порядок выполнения логических операций:

1)
2)
3)
4)
операция в скобках;
отрицание;
логическое умножение;
логическое сложение;
18

13. ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ ДЛЯ СЛОЖНЫХ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ.

23

14. При изучении работы различных устройств компьютера приходится рассматривать такие его логические элементы, в которых

реализуются
сложные логические выражения.
Поэтому необходимо научиться
определять результат этих выражений, то
есть строить для них
таблицы истинности.
24

15. Порядок построения таблиц истинности по булеву выражению:

• 1) определить число переменных;
• 2) определить число строк в таблице истинности:
q=2
n
• 3) записать все возможные значения переменных;
• 4) определить количество логических операций и
их порядок;
• 5) записать логические операции в таблицу
истинности и определить для каждой значение;
• 6) подчеркнуть значения переменных, для
которых F = 1.
26

16. Рассмотрим пример построения таблицы истинности для сложного (составного) логического выражения :

D A (B C)
25

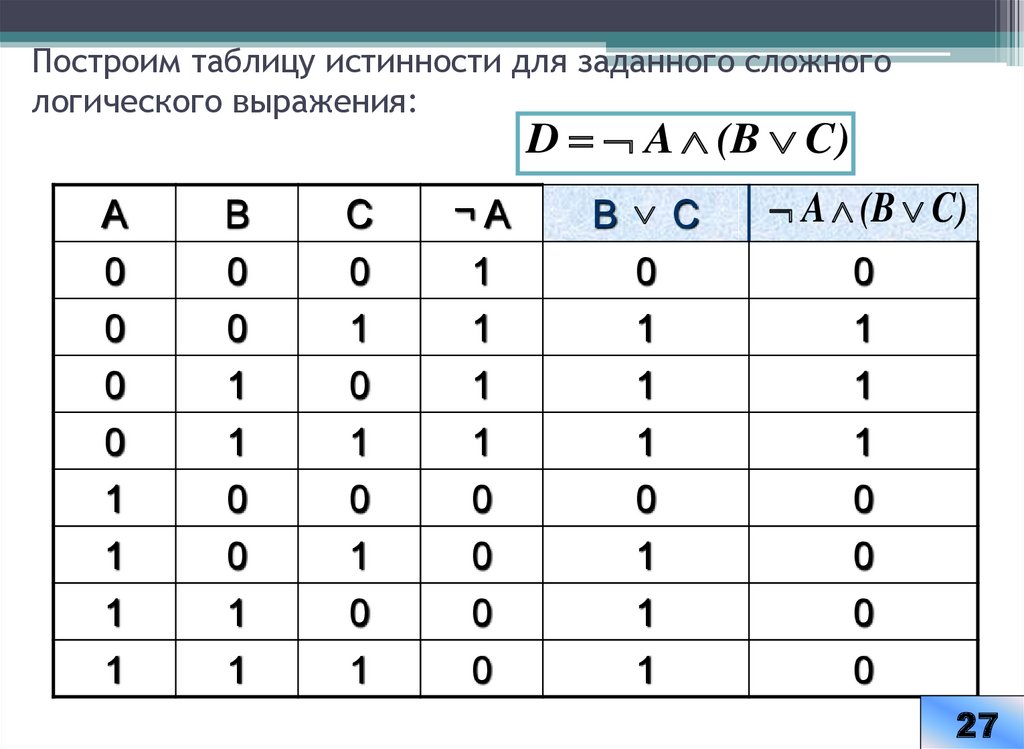
17. Построим таблицу истинности для заданного сложного логического выражения:

D A (B C)
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
¬A
1
1
1
1
0
0
0
0
B C
0
1
1
1
0
1
1
1
A (B C)
0
1
1
1
0
0
0
0
27

18. Задания: построить таблицы истинности для логических выражений:

1) D (A B C)
2) F (A B) C
3) F (A B C)
4) F A B C ( B C A)
31

19. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

33

20. Упрощённо можно представить работу компьютера как некоторого устройства, производящего обработку двоичных сигналов,

соответствующих 0 и 1. Такую обработку в
любом компьютере выполняют так называемые
логические элементы, из которых составляются
логические схемы, выполняющие различные
логические операции.
Реализация любых логических операций над
двоичными сигналами основана на использовании
логических элементов трех типов: И, ИЛИ, НЕ.
34

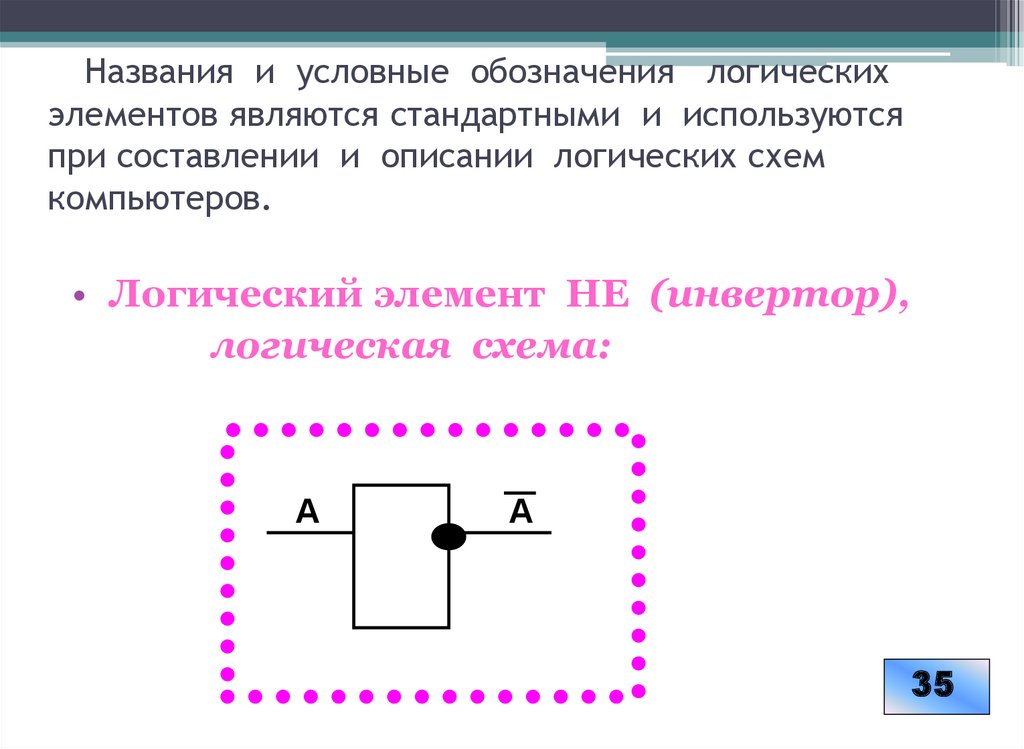
21. Названия и условные обозначения логических элементов являются стандартными и используются при составлении и описании логических

схем
компьютеров.
• Логический элемент НЕ (инвертор),
логическая схема:
А
А
35

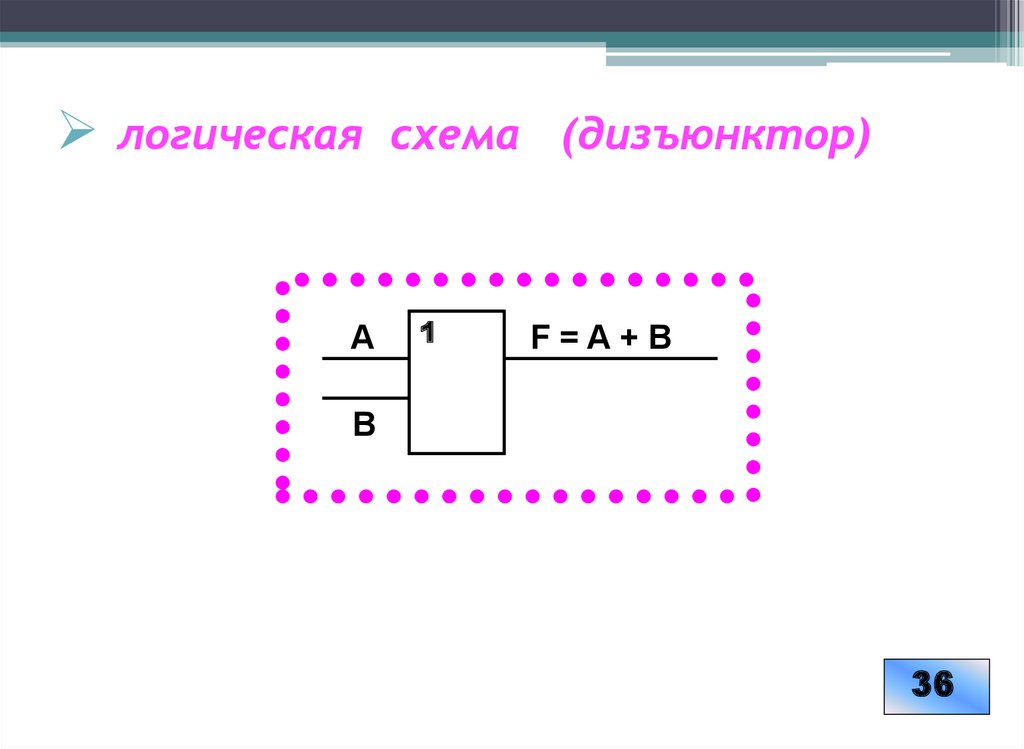
22. логическая схема (дизъюнктор)

А
1
F=A+B
В
36

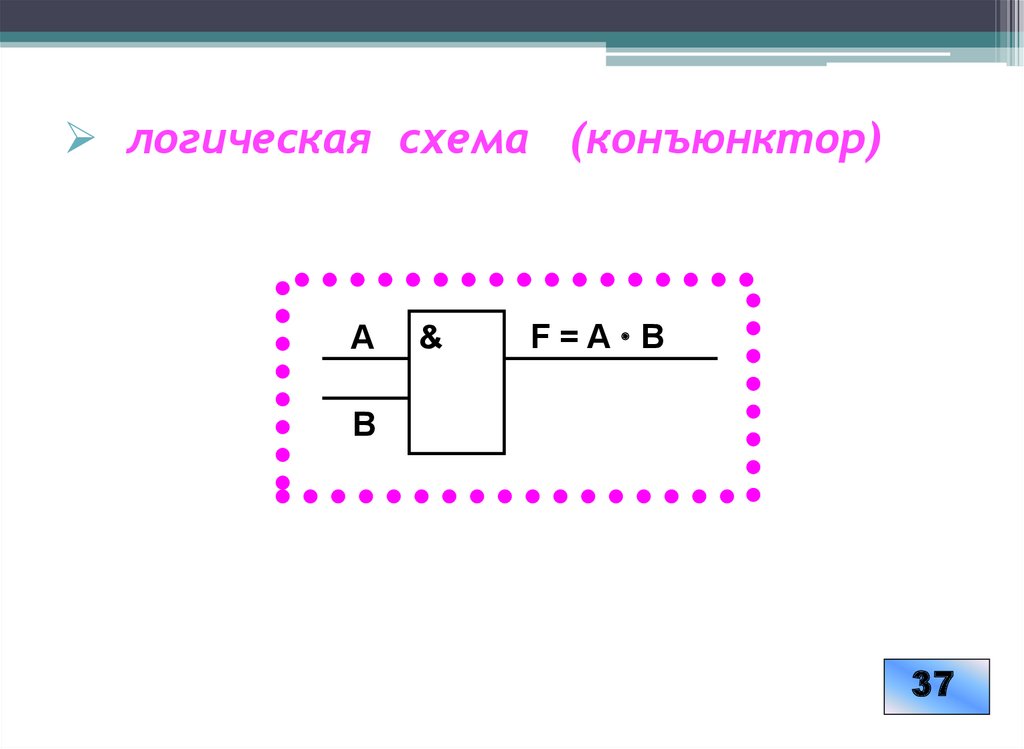
23. логическая схема (конъюнктор)

А
&
F=A B
В
37

24. Построение логических схем по булеву выражению:

• 1) определить число переменных;
• 2) определить количество логических
операций и их порядок;
• 3) построить для каждой логической
операции
свою схему (если это возможно);
• 4) объединить логические схемы в порядке
выполнения логических операций.
38

25. Рассмотрим пример построения логической схемы по булеву выражению :

D A (B C)
39

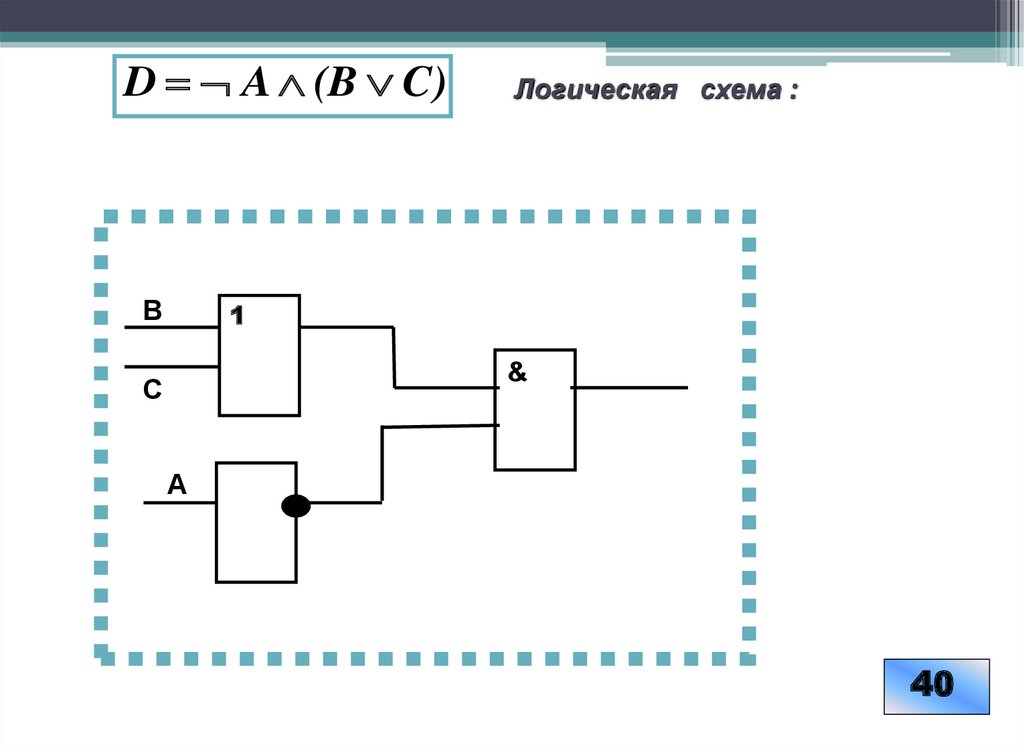
26.

D A (B C)
В
Логическая схема :
1
&
С
А
40

27. Задания: построить логические схемы по булевым выражениям:

1) D (A B C)
2) F (A B) C
3) F A B C
4 ) F A B C ( B C A )
42

28. Построение булева выражения по логической схеме:

1) на выходе каждого логического элемента
записать результат логической операции;
2) записать получившуюся формулу на выходе
последнего элемента;
3) упростить получившуюся формулу.
44

29. ТОЖДЕСТВА АЛГЕБРЫ ЛОГИКИ.

1)
2)
3)
4)
Логического
сложения
A+0=A
A+1=1
A+A=A
A+ A=1
(из двух противоречивых
высказываний хотя бы одно
истинно)
Логического
умножения
1)
2)
3)
4)
A
A
A
A
0 =0
1=A
A=A
A=0
(невозможно, чтобы одновременно
два противоположных
высказывания были истинны)
5) А = А
(двойное отрицание)
Распределительный закон:
(A + B) C = A C + B C
49

30.

Закон поглощения
A ( A B ) A B
A ( A B ) A B
A ( A B ) A
A ( A B ) A
Закон склеивания
( A B ) ( A B ) B
( A B ) ( A B ) A
54

31. Упростить логические выражения:

1) F B ( A A B)
2) F (A C) (A C) ( B C )
3) F A B A B A B B C
55