Механика жидкостей и газов

1.

ЛЕКЦИЯ 7
МЕХАНИКА ЖИДКОСТЕЙ И
ГАЗОВ

2.

Гидродинамика
раздел физики сплошных сред, изучающий движение идеальных и реальных
жидкости и газа. Как и в других разделах физики сплошных сред, прежде
всего осуществляется переход от реальной среды, состоящей из большого
числа отдельных атомов или молекул, к абстрактной сплошной среде, для
которой и записываются уравнения движения.
раздел
гидромеханики,
в котором
изучаются
движение
несжимаемых
жидкостей и
взаимодействи
е их с твёрдыми
телами.

3.

Давление в жидкости и газе
• Молекулы газа, совершая беспорядочное, хаотическое движение, не
связаны или весьма слабо связаны силами взаимодействия, поэтому
они движутся свободно и объем газа определяется объемом того
сосуда, который газ занимает.
• Жидкость, имея определенный объем, принимает форму того сосуда,
в который она заключена. В жидкостях среднее расстояние между
молекулами остается практически постоянным, поэтому жидкость
обладает практически неизменным объемом.
• Физическая величина, определяемая нормальной силой,
действующей со стороны жидкости (газа) на единицу площади,
называется давлением р жидкости (газа):
р = F/ S.
• Единица давления – паскаль (Па): 1 Па равен давлению,
создаваемому силой 1 Н, равномерно распределенной по
нормальной к ней поверхности площадью 1 м2 (1 Па =1 Н/м2).
3

4.

• Давление при равновесии жидкостей (газов) подчиняется
закону Паскаля: давление в любом месте покоящейся
жидкости одинаково по всем направлениям, причем давление
одинаково передается по всему объему, занятому покоящейся
жидкостью.
• Если жидкость несжимаема, то её плотность не зависит от
давления. Тогда при поперечном сечении S столба жидкости, его
высоте h и плотности r, вес столба жидкости P = r ·g·S·h, а
давление на нижнее основание
р = Р/ S = r ·g·S·h / S = r ·g·h,
т.е. давление изменяется линейно с высотой. Давление p·g·h
называется гидростатическим давлением.
• По закону Архимеда на тело, погруженное в жидкость (газ),
действует со стороны этой жидкости направленная вверх
выталкивающая сила, равная весу вытесненной телом
жидкости (газа):
FА = r·g·V,
где r – плотность жидкости, V – объем погруженного в
жидкость тела.
4

5.

Стационарное течение.
Условие неразрывности струи.
Уравнение Бернулли
• Движение жидкости называется течением, а
совокупность частиц движущейся жидкости
– потоком.
• Течение жидкости называется
установившимся или стационарным,
если форма и расположение линий тока, а
также значения скоростей в каждой ее точке
со временем не изменяется.

6.

Схематичное изображение
ламинарного (a) и турбулентного (b) течения в
плоском слое

7.

Рассмотрим стационарно текущую
идеальную жидкость

8.

• S1υ1 = S2υ2 = const (1)
• уравнение неразрывности
струи

9.

r
2
2
rgh p const
(8)
уравнение Бернулли
• где p - статистическое давление (на
поверхности);
r
- гидродинамическое
2
давление;
• rgh - гидростатическое давление.
2

10.

Вязкость жидкости Уравнение
Ньютона. Кровь, как
неньютоновская жидкость.
• При течении реальной жидкости
отдельные слои ее воздействуют друг
на друга с силами, касательными к
слоям. Это явление называют
внутренним трением или вязкостью.

11.

12.

d
Fтр S
dx
где η – коэффициент
пропорциональности, называемый
коэффициентом внутреннего трения
или динамической вязкостью.
(9)

13.

• Жидкости, вязкость которых не
зависит от градиента скорости
называются ньютоновскими.
• Жидкости, вязкость которых
зависит от градиента скорости
называются неньютоновскими.

14.

• Вязкость ньютоновских
жидкостей называют
нормальной,
• а неньютоновских –
аномальной.

15.

Кинематическая вязкость
В технике, в частности, при расчёте гидроприводов и в триботехнике,
часто приходится иметь дело с величиной
и эта величина получила название кинематической вязкости. Здесь
— плотность жидкости;
— динамическая вязкость
Кинематическая вязкость в старых источниках часто указана в
сантистоксах (сСт). В систему СИ эта величина переводится следующим
образом:
1 сСт = 1мм2/1c =
м2/c

16.

Течение вязкой жидкости по
трубам. Формула Пуазейля.
Гидравлическое сопротивление
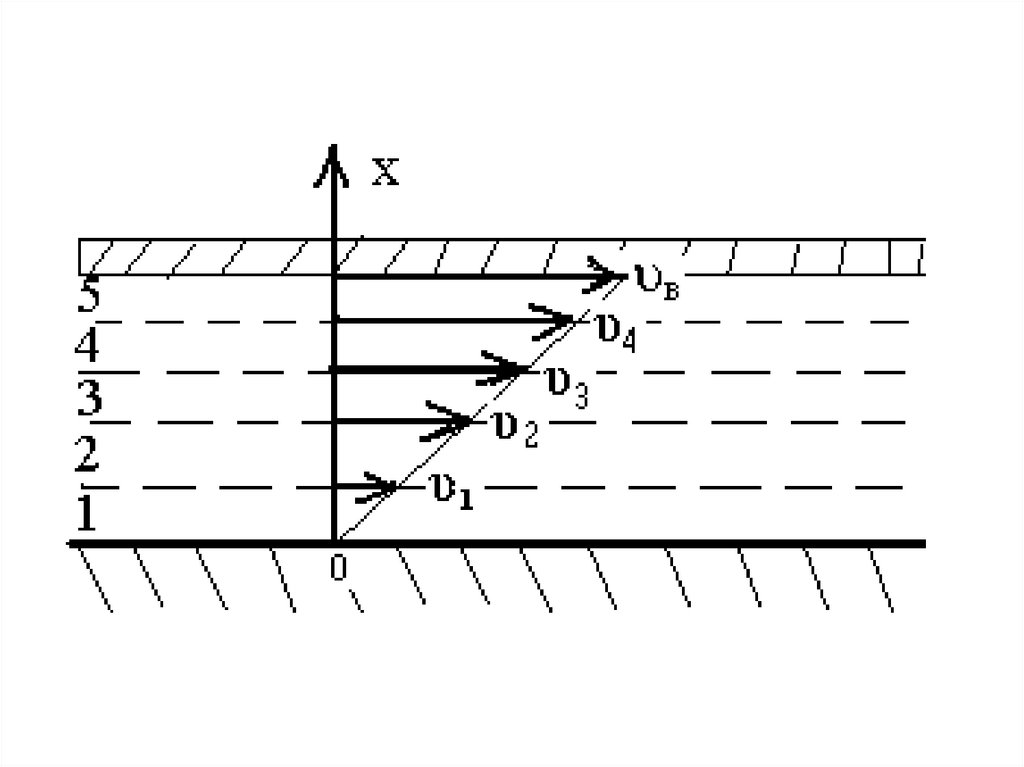
• Распределение скорости частиц жидкости в
сечении трубы

17.

• Цилиндрический объем жидкости
некоторого радиуса r и длины l.

18.

• На торцах этого цилиндра
поддерживается давление p1 и p2
соответственно, что обуславливает
результирующую силу
• F = p1πr2– p2πr2 = ( p1 – p2)πr2 (10)

19.

• На боковую поверхность цилиндра
со стороны окружающего слоя
жидкости действует сила
внутреннего трения, равная:
d
Fтр S =
dx
d
2 r
dr
где S = 2πrl – площадь боковой
поверхности цилиндра.
(11)

20.

• Так как жидкость движется
равномерно, то силы,
действующие на выделенный
цилиндр, уравновешены:
• F = Fтр
(12)
Следовательно:
d
• (p1 – p2)πr2 = – 2 r
dr
(13)

21.

• из выражения (13) имеем:
• dυ =
p1 p 2
rdr
2
(14)
• Проинтегрировав выражение (14)
получим:
•υ =
p1 p 2 2 2
(R r )
2
(15)

22.

• Наибольшую скорость имеет слой, текущий
вдоль оси трубы (r=0):
• υmax =
( p1 p 2 ) R
4
2
(16)

23.

• Установим, от каких факторов
зависит объем Q жидкости,
протекающей через
горизонтальную трубу за 1 с. Для
этого выделим цилиндрический
слой радиусом r и толщиной dr.
Площадь сечения этого слоя
• dS = 2πrdr

24.

• Так как слой тонкий, то можно
считать, что он перемещается с
одинаковой скоростью υ. За 1 с
слой переносит объем жидкости:
• dQ = υdS = υ2πrdr
(17)
• Подставим (16) в (17) получим:
p1 p 2 2 2
(R r )rdr (18)
• dQ =
2

25.

• Проинтегрируем (18) по всему
сечению, получим:
p1 p 2
R
• Q=
8
4
(19)
(19) формула Пуазейля.
• X=8η /(πR4) – гидравлическое
сопротивление.

26.

• При последовательном соединении
сосудов:
• Х = Х1+Х2+Х3
(20)
• При параллельном:
• Х=
1
1
1
X1 X 2 X 3
1
(21)

27.

Ламинарное и турбулентное
течение. Число Рейнольдса.
• Рассмотренное ранее течение
жидкости является слоистым, или
ламинарным.
• Увеличение скорости течения вязкой
жидкости по поперечному сечению
трубы создает завихрение, и движение
становится вихревым или
турбулентным.

28.

• Характер течения жидкости по трубе
зависит от свойств жидкости, скорости
ее течения, размеров трубы
определяется числом Рейнольдса:
• Rе = ρжυD/η
(22)
• где ρж – плотность жидкости;
• D – диаметр трубы

29.

• Так как число Рейнольдса зависит от
вязкости и плотности жидкости, то
удобно ввести их соотношение,
называемое кинематической
вязкостью:
• ν = η/ρж (м2/с)
(23)
• Используя это понятие, число
Рейнольдса можно выразить в виде:
• Rе = υD/ν
(24)