Инновационный менеджмент и стратегическое управление

1.

Подготовили студентки БМО 21
Муренцева В.
Кривонос В.

2.

Стратегическое управление инновациями является составной
частью инновационного менеджмента и решает вопросы
планирования и реализации инновационных проектов,
рассчитанных на значительный качественный скачок в
предпринимательстве, производстве или социальной среде
предприятия.
По своей сущности любые стратегические меры, принимаемые
предприятием, носят инновационный характер, поскольку они так
или иначе основаны на нововведениях в его экономическом,
производственном или сбытовом потенциалах.
Стратегия нововведений (инновационная политика) предполагает
объединение целей технической политики и политики
капиталовложений и направлена на внедрение новых технологий и
видов продукции.
Она предусматривает выбор определенных объектов
исследований, с помощью которых предприятие в первую очередь
осуществляет систематический поиск новых технологических
возможностей.
Общий менеджмент определяет генеральную линию
стратегического развития и включает:
1. нормативный менеджмент — разработка философии,
предпринимательской политики, определение позиции
предприятия в конкретной нише рынка; формулирование общих
стратегических намерений;
2. стратегический менеджмент — выработка набора стратегий, их
реализация во времени, фиксирование изменений,
переформулирование стратегий, стратегический контроль,
управление стратегическими решениями в целом;
3. оперативный менеджмент — разработка и реализация
оперативных (тактических) мер, связанных с практическим
осуществлением мероприятий по внедрению стратегий в действие.

3.

Цели стратегического управления инновациями подразделяют на:
- функциональные (поддержание достигнутого состояния системы);
- новые (приобретение нового качественного состояния системы).
Новые цели требуют выхода на новые ориентиры, новые критерии равновесия в системе, новые решения, новые
организационные структуры, то есть вызывают необходимость разработки и осуществления комплекса действий,
которые определяются как стратегии.
Стратегия в общем виде — это поиск наиболее результативных вариантов ввода в действие ресурсов (капитала,
рабочей силы) в соответствии с главными целями предприятия и с учетом ситуации на рынке как в настоящий
момент, так и ожидаемой в будущем.
Стратегия предполагает разработку обоснованных мер и планов (программ, проектов) достижения намеченных
целей, в которых должны быть учтены научно-технический и производственный потенциалы предприятия и его
рыночно-сбытовые возможности. Стратегические цели отражают генеральную линию развития ИП. Стратегическая
цель ориентирована на решение той или иной проблемы, или задачи, связанной с рынком или с принципиальным
вопросом выживаемости инновационного предприятия.
Постановка и формулирование стратегических целей служат исходной базой для выбора и разработки
обеспечивающих их достижение стратегий.

4.

Процесс создания инновационной продукции на промышленном предприятии связан не только со
значительными инвестициями, но и рисками на всех этапах жизненного цикла.
В связи с этим на практике постоянно встает вопрос об эффективности вкладываемых инвестиций
в инновационные проекты и разработки такого механизма управления инновационным риском,
который позволял бы сократить потери эффекта от инвестиций и, в свою очередь, повысить
эффективность инновационной деятельности.
На заключительных этапах жизненного цикла на эффективность инвестиций оказывают
значительное влияние преимущественно рыночные риски. Однако на начальных этапах
жизненного цикла проекта значительное влияние на эффективность инвестиций оказывают
инновационные риски .
К их числу можно отнести: риски отрицательных результатов испытаний продукции, патентного
анализа, уникальности сырьевых и материальных ресурсов, необходимых для изготовления
инновационной продукции и др.
Для решения проблемы оценки риска изменчивости инновационного проекта разработана
методика, которая основана на моделировании бизнес-процессов этапов инновационных проектов
сетевыми графами и использовании методологии имитационного моделирования.

5.

Сетевое моделирование — это один из методов
системного подхода к управлению сложными
динамическими системами с целью обеспечения
определенных оптимальных показателей. В основе
сетевого моделирования лежит изображение
планируемого комплекса работ в виде графа.
Дадим некоторые основные определения:
Граф — это схема, состоящая из заданных точек
(вершин), соединенных определенной системой
линий. Отрезки, соединяющие вершины,
называются ребрами (дугами) графа.
Сетевой график — это ориентированный граф без
контуров, ребра которого имеют одну или
несколько числовых характеристик. В сетевом
графике различают два основных элемента:
работу и событие.

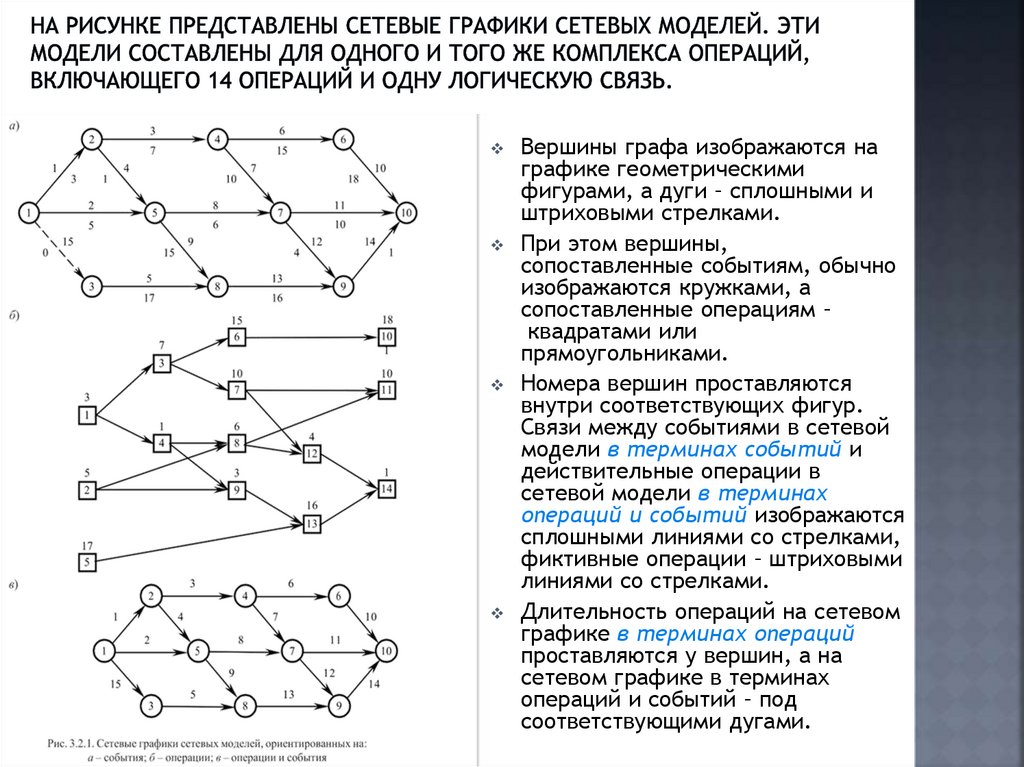
6.

В зависимости от цели моделирования сетевые
модели могут быть ориентированы либо на
события, либо на операции, либо на операции
и события.
Сетевая модель, Сетевая модель, Сетевая модель,
ориентированная ориентированная ориентированная
на события
на операции
на операции и
события
Сеть,
в которой
вершинам
сопоставлены
события, а дугам
– связи между
ними.
Сеть, в
которой
вершинам
сопоставлены
операции, а
дугам – связи
между ними.
Сеть, в которой
вершинам
сопоставлены
события, а дугам
– операции.
Эти сетевые модели называют также моделями в
терминах событий, операций, операций и событий
соответственно.

7.

Вершины графа изображаются на
графике геометрическими
фигурами, а дуги – сплошными и
штриховыми стрелками.
При этом вершины,
сопоставленные событиям, обычно
изображаются кружками, а
сопоставленные операциям –
квадратами или
прямоугольниками.
Номера вершин проставляются
внутри соответствующих фигур.
Связи между событиями в сетевой
модели в терминах событий и
действительные операции в
сетевой модели в терминах
операций и событий изображаются
сплошными линиями со стрелками,
фиктивные операции – штриховыми
линиями со стрелками.
Длительность операций на сетевом
графике в терминах операций
проставляются у вершин, а на
сетевом графике в терминах
операций и событий – под
соответствующими дугами.

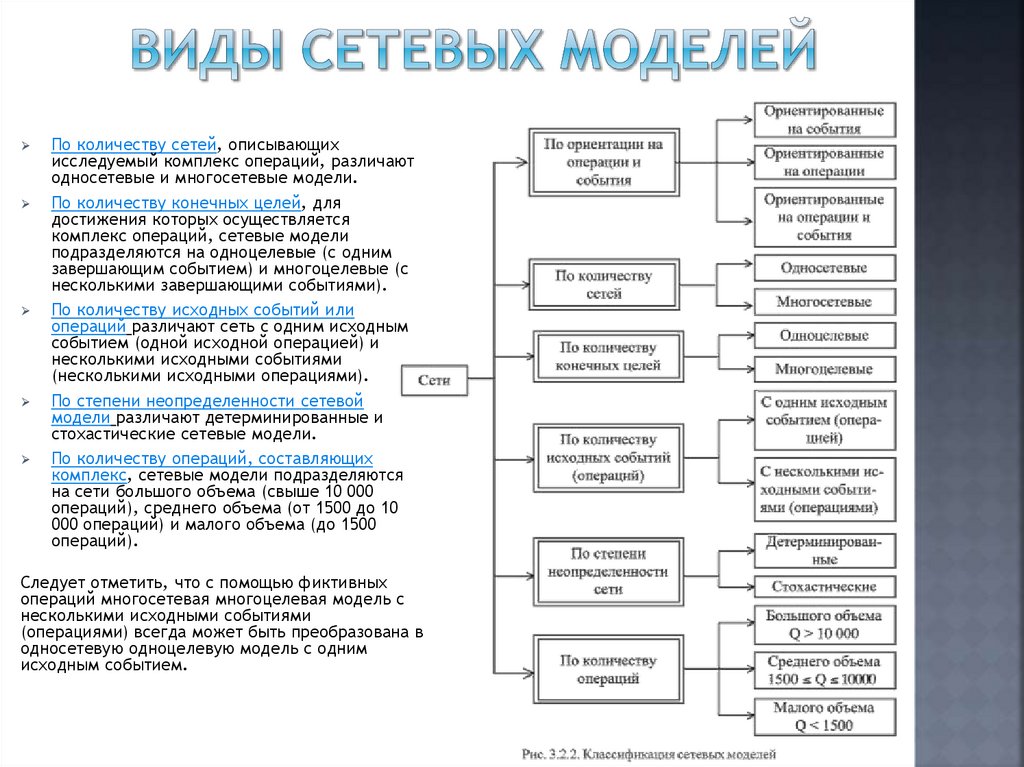
8.

По количеству сетей, описывающих
исследуемый комплекс операций, различают
односетевые и многосетевые модели.
По количеству конечных целей, для
достижения которых осуществляется
комплекс операций, сетевые модели
подразделяются на одноцелевые (с одним
завершающим событием) и многоцелевые (с
несколькими завершающими событиями).
По количеству исходных событий или
операций различают сеть с одним исходным
событием (одной исходной операцией) и
несколькими исходными событиями
(несколькими исходными операциями).
По степени неопределенности сетевой
модели различают детерминированные и
стохастические сетевые модели.
По количеству операций, составляющих
комплекс, сетевые модели подразделяются
на сети большого объема (свыше 10 000
операций), среднего объема (от 1500 до 10
000 операций) и малого объема (до 1500
операций).
Следует отметить, что с помощью фиктивных
операций многосетевая многоцелевая модель с
несколькими исходными событиями
(операциями) всегда может быть преобразована в
односетевую одноцелевую модель с одним
исходным событием.

9.

При построении сетевой модели ее вершинам обычно присваиваются числа, которые служат
номерами вершин. Тогда каждой дуге сети может быть сопоставлена пара чисел, первое из
которых соответствует вершине, из которой исходит дуга, а второе – вершине, в которую
заходит дуга.
Основные правила построения:
Для каждой вершины сети номер любой предшествующей ей вершины должен быть меньше
ее собственного номера.
В сетевой модели не должно быть "лишних" висячих и тупиковых вершин, т. е. таких
висячих вершин, которые не соответствуют исходным событиям и операциям, и таких
тупиковых вершин, которые не соответствуют завершающим событиям и операциям.
В сети не должно быть петель, контуров и кратных дуг.
В сети должны быть только одна исходная и одна завершающая
вершины.
Выполнение данных правил облегчает построение и контроль правильности построения
сетевой модели, а также позволяет применять существующие программы для расчета
параметров и анализа сетей на ЭВМ.

10.

Широкое распространение сетевого моделирования
при решении практических задач управления
обусловлено тем, что она позволяет реализовывать
системный подход, применять математические
методы и современную вычислительную технику при
исследовании сложных процессов, повышать
эффективность планирования и управления такими
процессами.

11.

Граф -это множество точек или вершин и множество линий или ребер,
соединяющих между собой все или часть этих точек.
Графы возникли в восемнадцатом столетии, когда известный математик,
Леонард Эйлер, пытался решить теперь уже классическую задачу о
Кенигсбергских мостах.
В то время в городе Кенигсберге было два острова, соединенных семью
мостами с берегами реки Преголь и друг с другом так, как показано на
рисунке.
Задача состоит в следующем: осуществить прогулку по городу таким
образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться
в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер
изобразил Кенигсберг в виде графа, отождествив его вершины с частями
города, а ребра — с мостами, которыми связаны эти части.

12.

Модель задачи — это граф, состоящий из множества вершин и множества ребер, соединяющих
вершины. Вершины A, B , С и D символизируют берега реки и острова, а ребра а, b, с, d, е, f и g
обозначают семь мостов. Искомый маршрут соответствует обходу ребер графа таким образом, что
каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки
по мосту. Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и
проходящий по всем ребрам графа ровно один раз, называется эйлеровым графом. Последовательность
вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут,
называется эйлеровым циклом.
Простой граф определяется как пара G = (V, Е),где V — конечное множество вершин, а, Е — конечное
множество ребер, при чем G не может содержать петель (ребер, начинающихся и заканчивающихся в
одной вершине) и кратных ребер (кратными называются несколько ребер, соединявших одну и ту же
пару вершин). Граф, изображенный на рисунке, не является простым, поскольку, например, вершины А
и В соединяются двумя ребрами (как раз эти ребра и называются кратными). Также некоторые важные
обозначения, используемые в теории графов:
|V| – порядок (число вершин);
|E| – размер графа (число рёбер)
В данном случае |V|=4, |E|=7;

13.

Когда из любой связанной вершины можно перейти в другую вершину и обратно, то
такой граф называется неориентированным (рис. 1). Если же это условие не
выполняется (ребра являются направленными), тогда такой граф называется
ориентированным или орграфом (рис. 2).
В ориентированных и неориентированных графах имеется понятие степени вершины.
Степень вершины – это количество ребер соединяющих ее с другими вершинами.
Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для
рисунка 1-2 сумма всех степеней равна 20.
В орграфе, в отличие от неориентированного графа, имеется возможность двигаться
из вершины a в вершину b без промежуточных вершин, лишь тогда когда ребро
выходит из f и заходит в b, но не наоборот.
Ориентированные графы имеют следующую форму записи:
G=(V, A), где V – вершины, A – направленные ребра.
Третий тип графов – смешанные графы (рис. 3). Они могут иметь как направленные
ребра, так и ненаправленные. Форма записи данного типа: G=(V, E, A), где каждая из
букв в скобках означает тоже, что ей приписывалось ранее. Тут одни дуги
направленные [(e, a), (e, с), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e,
b), (d, c)…].

14.

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает
вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4.11).
Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие
графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с
определенным числом ребер в одном графе имеет тождественную вершину в другом. Выше изображены
два изоморфных графа.
Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра,
тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды
измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые
значения указываются, как правило, рядом с ребрами.
В любом из графов имеется возможность выделить путь и, причем не один.
Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра.
Если первая и последняя вершины совпадают, то такой путь называется циклом.
Длина пути определяется количеством составляющих его ребер.

15.

Не имеет значения, как нарисовать граф, поскольку все его изображения являются изоморфными
графами и несут одну и ту же информацию. Однако встречаются ситуации, когда крайне важно, чтобы
изображение графа на плоскости удовлетворяло определенным требованиям.
В радиоэлектронике при изготовлении микросхем печатным способом электрические цепи наносятся
на поверхность изоляционного материала. А так как проводники не изолированы, то они не должны
пересекаться.
Аналогичная задача возникает при проектировании железнодорожных и иных путей, где
нежелательны переезды.
Геометрический граф назовем плоским графом, если он нарисован на плоскости так, что все линии,
изображающие его ребра, пересекаются только в точках, соответствующих вершинам графа, т.е. любая
точка пересечения таких линий есть вершина, инцидентная ребрам, которые эти линии изображают.
Любой граф, изоморфный плоскому графу, называют планарным.
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку).
Планарный граф можно уложить на плоскости, а плоский граф - это граф, уже уложенный на плоскости.
Плоский граф есть изображение планарного графа, однако не каждое изображение планарного графа
является плоским графом.

16.

Матрица инцинденций. Это
матрица А с n строками, соответствующими
вершинам, и m столбцами, соответствующего
рёбрам. Для ориентированного графа столбец,
соответствующий дуге (х,y) содержит - 1 в
строке, соответствующей вершине х и 1, в
строке, соответствующей вершине у. Во всех
остальных 0. Петлю, т.е. дугу (х,х) можно
представлять иным значением в строке х,
например, 2.
Матрица смежности. Это матрица n×n где n число вершин, где bij = 1, если существует
ребро, идущее из вершины х в вершину у и bij =
0 в противном случае.
Матрица инцидентности, как и матрица смежности,
однозначно определяет граф. Существуют приемы
перехода от одной матрицы к другой.
С помощью матриц смежности можно установить
изоморфизм графов. Для этого необходимо в
матрице смежности одного графа проделать
перестановки строк и столбцов. Если после
очередной перестановки получим матрицу,
тождественно совпадающую с матрицей другого
графа, то графы изоморфны.

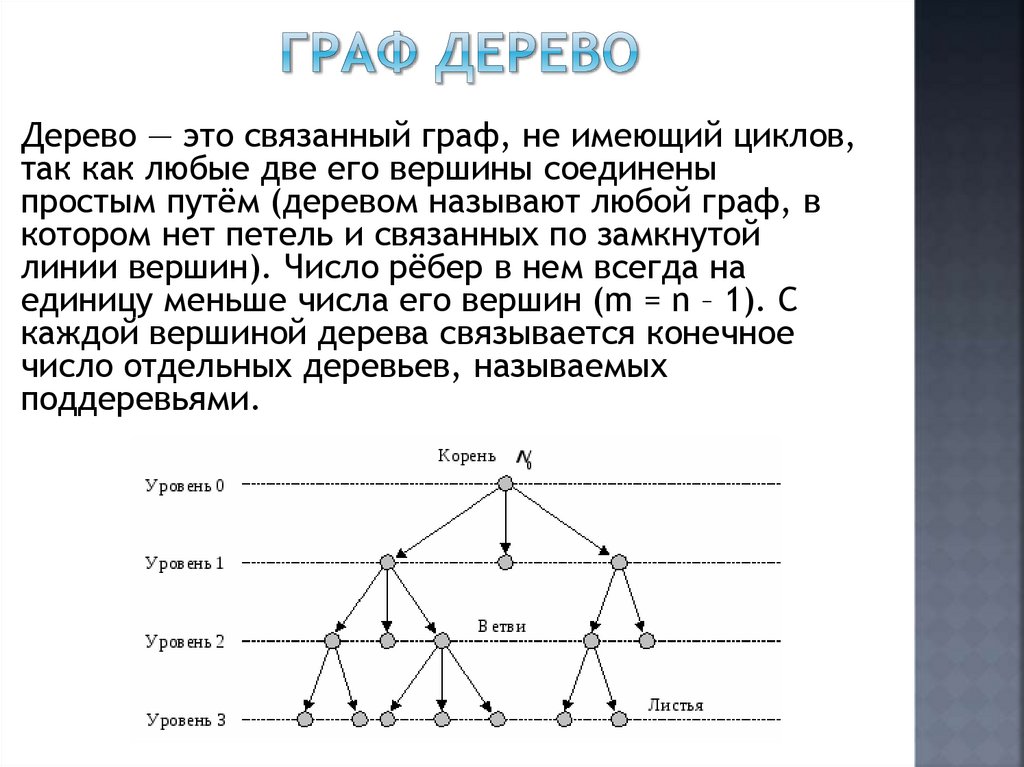
17.

Дерево — это связанный граф, не имеющий циклов,
так как любые две его вершины соединены
простым путём (деревом называют любой граф, в
котором нет петель и связанных по замкнутой
линии вершин). Число рёбер в нем всегда на
единицу меньше числа его вершин (m = n – 1). С
каждой вершиной дерева связывается конечное
число отдельных деревьев, называемых
поддеревьями.

18.

Примерами деревьев могут служить генеалогические и
организационные диаграммы. Деревья используются при
анализе электрических цепей, при представлении
структур математических формул. Деревья используются
для организации информации в системах управления
базами данных (иерархическая база данных).

19.

Язык графов оказывается удобным для описания многих
физических, технических, экономических,
биологических, социальных и других систем.
«Транспортные» задачи, в которых вершинами графа
являются пункты, а ребра – дороги или другие
транспортные маршруты.
Сети снабжения (энергоснабжения, газоснабжения,
снабжения товарами и т. д.), в которых вершинами
являются пункты производства и потребления, а
ребрами – возможные маршруты перемещения
(линии электропередач, газопроводы, дороги и т.
д.).
«Технологические задачи», в которых вершины
отражают производственные элементы (заводы,
цеха, станки и т. д.), а дуги – потоки сырья,
материалов и продукции между ними, заключаются в
определении оптимальной загрузки
производственных элементов и обеспечивающих эту
загрузку потоков.
Обменные схемы, являющиеся моделями таких
явлений как бартер, взаимозачёты и т. д. Вершины
графа при этом описывают участников обменной
схемы, а дуги – потоки материальных и финансовых
ресурсов между ними. Задача заключается в
определении цепочки обменов, оптимальной с точки
зрения, например, организатора обмена и
согласованной с интересами участников цепочки и
существующими ограничениями.

20.

Управление проектами. С точки зрения теории графов –
совокупность операций и зависимостей между ними
(сетевой график). Примером является проект
строительства некоторого объекта. Совокупность
моделей и методов, использующих язык и результаты
теории графов и ориентированных на решение задач
управления проектами, получила название календарносетевого планирования и управления (КСПУ). В рамка
КСПУ решаются задачи определения
последовательности выполнения операций и
распределения ресурсов между ними, оптимальных с
точки зрения тех или иных критериев (времени
выполнения проекта, затрат риска и др.).
Модели коллектива и групп, используемые в
социологии, основываются на представлении людей
или их групп в виде вершин, а отношений между ними
(например, отношений знакомства, доверия, симпатии
и т. д.) – в виде рёбер или дуг. Тем самым решаются
задачи исследования структуры социальных групп, их
сравнения и т. д.
Модели организационных структур, в которых
вершинами являются элементы организационной
системы, а рёбрами или дугами – связи
(информационные, управляющие, технологические и
др.) между ними.

21.

Сетевое планирование — метод анализа сроков
(ранних и поздних) начала и окончания
нереализованных частей проекта, позволяет
увязать выполнение различных работ и
процессов во времени, получив прогноз общей
продолжительности реализации всего проекта.
Основная цель сетевого планирования сокращение до минимума продолжительности
проекта.
Задача сетевого планирования состоит в том,
чтобы графически, наглядно и системно
отобразить и оптимизировать
последовательность и взаимозависимость
работ, действий или мероприятий,
обеспечивающих своевременное и
планомерное достижение конечных целей.
Для отображения и алгоритмизации тех или
иных действий или ситуаций используются
экономико-математические модели, которые
принято называть сетевыми моделями,
простейшие из них - сетевые графики.
С помощью сетевой модели руководитель
работ или операции имеет возможность
системно и масштабно представлять весь ход
работ или оперативных мероприятий,
управлять процессом их осуществления, а
также маневрировать ресурсами.

22.

Структурное планирование начинается с разбиения проекта на четко определенные
операции, для которых определяется продолжительность. Затем строится сетевой
график, который представляет взаимосвязи работ проекта. Это позволяет детально
анализировать все работы и вносить улучшения в структуру проекта еще до начала
его реализации.
Календарное планирование предусматривает построение календарного графика,
определяющего моменты начала и окончания каждой работы и другие временные
характеристики сетевого графика. Это позволяет, в частности, выявлять
критические операции, которым необходимо уделять особое внимание, чтобы
закончить проект в директивный срок.
Во время календарного планирования определяются временные характеристики всех
работ с целью проведения оптимизации сетевой модели, которая улучшает
эффективность использования какого-либо ресурса.
В ходе оперативного управления используются сетевой и календарный графики для
составления периодических отчетов о ходе выполнения проекта. При этом сетевая
модель может подвергаться оперативной корректировке, вследствие чего будет
разрабатываться новый календарный план остальной части проекта.

23.

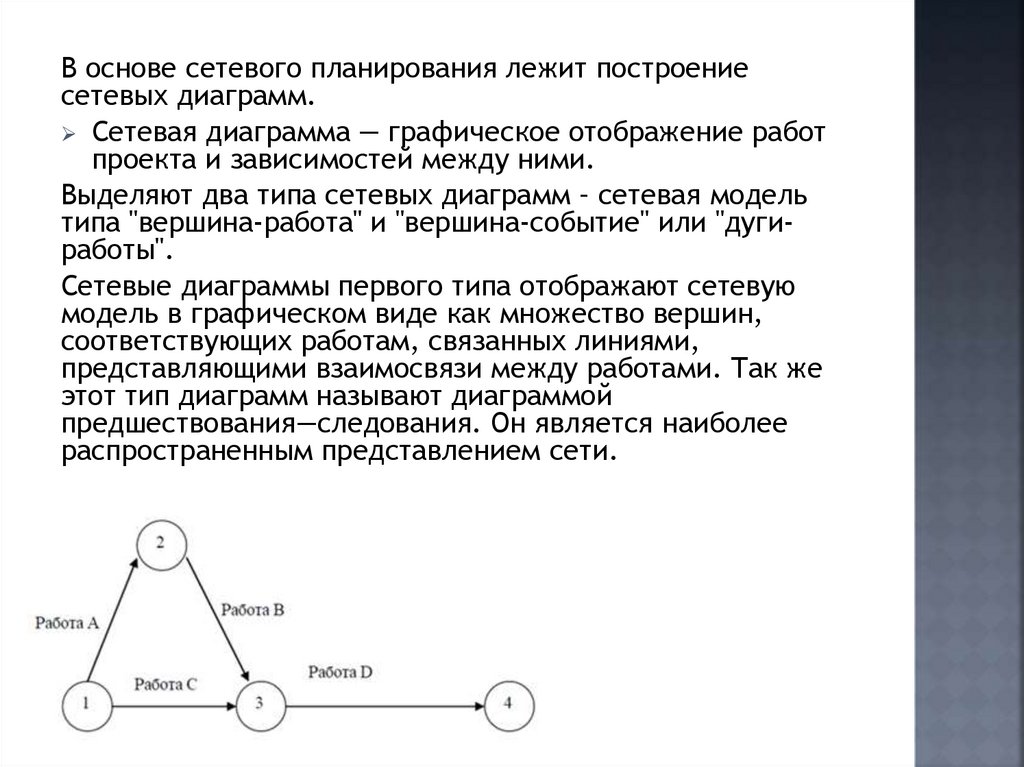
В основе сетевого планирования лежит построение
сетевых диаграмм.
Сетевая диаграмма — графическое отображение работ
проекта и зависимостей между ними.
Выделяют два типа сетевых диаграмм – сетевая модель
типа "вершина-работа" и "вершина-событие" или "дугиработы".
Сетевые диаграммы первого типа отображают сетевую
модель в графическом виде как множество вершин,
соответствующих работам, связанных линиями,
представляющими взаимосвязи между работами. Так же
этот тип диаграмм называют диаграммой
предшествования—следования. Он является наиболее
распространенным представлением сети.

24.

Другой тип сетевой
диаграммы — сеть типа
"вершина—событие", на
практике используется
реже.
При данном подходе
работа представляется в
виде линии между двумя
событиями (узлами
графа), которые, в свою
очередь, отображают
начало и конец данной
работы.
PERT-диаграммы являются
примерами этого типа
диаграмм.

25.

Детерминированные сетевые методы;
Диаграмма Ганта
Метод критического пути (МКП)
Вероятностные сетевые методы;
Неальтернативные
1. Метод имитационного моделирования
(метод Монте-Карло)
2. Метод оценки и пересмотра планов (PERT)
Альтернативные
1. Метод графической оценки
и анализа (GERT).

26.

Диаграмма Ганта — это тип столбчатых диаграмм, который используется для иллюстрации плана,
графика работ по какому-либо проекту. Является одним из методов планирования проектов.
Используется в приложениях по управлению проектами.
Диаграмма представляет собой ряд полос, состоящий из двух осей. Горизонтальная ось
называется осью времени, а вертикальная ось – это перечень задач, которые необходимо
выполнить в рамках проекта.
Диаграмма включает набор полос на графике, которые располагаются вдоль временной оси.
Конец каждой полосы – это время окончания старой задачи и начало новой.
Длина каждой полосы указывает на продолжительность срока, во время которого выполняется
конкретная задача.
Кроме основных данных на диаграмме Ганта принято отображать и некоторые дополнительные
данные. К примеру, процент выполнения каждой задачи, последовательность действий, отметка
ключевых моментов и отметка времени.

27.

Метод критического пути - инструмент планирования расписания и управления сроками
проекта.
В основе метода лежит определение наиболее длительной последовательности задач от
начала проекта до его окончания с учетом их взаимосвязи.
Задачи, лежащие на критическом пути, имеют нулевой резерв времени выполнения, и, в
случае изменения их длительности, изменяются сроки всего проекта. В связи с этим, при
выполнении проекта критические задачи требуют более тщательного контроля, в
частности, своевременного выявления проблем и рисков, влияющих на сроки их
выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе
выполнения проекта критический путь проекта может меняться, так как при изменении
длительности задач некоторые из них могут оказаться на критическом пути.
Применение метода критического пути для разработки календарного графика реализации
работ по проекту предусматривает в основном выполнение четырех этапов анализа. Но их
может быть намного больше, если проект более масштабный.
Цели и
ограничения
Продолжите
льность
работ
Сетевой
график
работ
Линейная
диаграмма
Ганта и
сетевой
график

28.

Первый этап
Чтобы установить цели и ограничения в рамках планирования по методу критического пути,
необходимо рассмотреть проект в следующих аспектах:
продолжительность;
стоимость;
качество;
наличие производственных ресурсов (рабочая сила и оборудование);
другие важные аспекты.
Второй этап планирования по методу критического пути представляет собой определение работ,
входящий в проект, и расчете длительности каждой работы.
Третий этап планирования по методу критического пути включает в себя анализ установки очередности работ и
составление графика, отражающего последовательность работ.
Некоторые работы должны производиться в определенной последовательности, некоторые можно выполнять
параллельно.
Очередность работ в основном определяется техническими причинами.
Четвертый этап планирования по методу критического пути предусматривает построение диаграммы Ганта и календарного
сетевого графика на основе оценок продолжительности работ и полученной сетки.

29.

В рамках метода Монте-Карло анализ риска выполняется с помощью моделей
возможных результатов. При создании таких моделей любой фактор, которому
свойственна неопределенность, заменяется диапазоном значений —
распределением вероятностей.
Затем выполняются многократные расчеты результатов, причем каждый раз
используется другой набор случайных значений функций вероятности. Порой для
завершения моделирования бывает необходимо произвести тысячи и даже десятки
тысяч перерасчетов — в зависимости от количества неопределенностей и
установленных для них диапазонов. Моделирование по методу Монте-Карло
позволяет получить распределения значений возможных последствий.
При использовании распределений вероятностей переменные могут иметь разные
вероятности наступления разных последствий. Распределения вероятностей
представляют собой гораздо более реалистичный способ описания
неопределенности переменных в процессе анализа риска. Далее перечислены
наиболее распространенные распределения вероятностей.

30.

Нормальное распределение (или « гауссова кривая
»). Чтобы описать отклонение от среднего, пользователь
определяет среднее или ожидаемое значение и
стандартное отклонение.
Логнормальное распределение. Значения имеют
положительную асимметрию и несимметричны. Такое
распределение используется для отражения величин,
которые не опускаются ниже нуля, но могут принимать
неограниченные положительные значения.
Равномерное распределение. Все величины могут с равной
вероятностью принимать то или иное значение,
пользователь просто определяет минимум и максимум.
Треугольное распределение. Пользователь определяет
минимальное, наиболее вероятное и максимальное
значения.
Дискретное распределение. Пользователь определяет
конкретные значения из числа возможных, а также
вероятность получения каждого из них.
При моделировании по методу Монте-Карло значения
выбираются случайным образом из исходных
распределений вероятности. Каждая выборка значений
называется итерацией; полученный из выборки результат
фиксируется. В процессе моделирования такая процедура
выполняется сотни или тысячи раз, а итогом становится
распределение вероятностей возможных последствий.
Таким образом, моделирование по методу Монте-Карло дает
гораздо более полное представление о возможных событиях.
Оно позволяет судить не только о том, что может произойти, но
и о том, какова вероятность такого исхода.

31.

Моделирование по методу Монте-Карло имеет ряд
преимуществ:
Вероятностные результаты. Результаты
демонстрируют не только возможные события, но и
вероятность их наступления.
Графическое представление результатов. Характер
данных, получаемых при использовании метода
Монте-Карло, позволяет создавать графики
различных последствий, а также вероятностей их
наступления.
Анализ чувствительности. При проведении
моделирования по методу Монте-Карло несложно
увидеть, какие исходные данные оказывают
наибольшее воздействие на конечные результаты.
Анализ сценариев. Применяя метод Монте-Карло,
аналитики могут точно определить, какие исходные
данные приводят к тем или иным значениям, и
проследить наступление определенных
последствий. Это очень важно для проведения
дальнейшего анализа.
Корреляция исходных данных. Метод Монте-Карло
позволяет моделировать взаимозависимые
отношения между исходными переменными. Для
получения достоверных сведений необходимо
представлять себе, в каких случаях при увеличении
некоторых факторов соответствующим образом
возрастают или снижаются другие.

32.

Program Evaluation and Review Technique — техника оценки и анализа программ, которая используется при управлении
проектами.
PERT обеспечивает оценку и анализ времени выполнения, трудозатрат и потребности в других ресурсах проекта, на
основе соответствующих характеристик и зависимостей входящих в него задач. В особенности, анализа и оценки
времени, которое требуется для выполнения каждой отдельной задачи, а также минимально необходимого времени
для выполнения всего проекта.
PERT была разработана главным образом для упрощения планирования и составления графиков больших и сложных
проектов. PERT предназначена для очень масштабных, единовременных, сложных, не рутинных проектов. Техника
подразумевала наличие неопределённости, давая возможность разработать рабочий график проекта без точного знания
деталей и необходимого времени для всех его составляющих.
Диаграмма PERT с работами на стрелках представляет собой множество точек-вершин (события) вместе с
соединяющими их ориентированными дугами (работы). Всякой дуге, рассматриваемой в качестве какой-то работы из
числа нужных для осуществления проекта, приписываются определенные количественные характеристики.
Это — объёмы выделяемых на данную работу ресурсов и, соответственно, её ожидаемая продолжительность (длина
дуги). Любая вершина интерпретируется как событие завершения работ, представленных дугами, которые входят в
неё, и одновременно начала работ, отображаемых дугами, исходящими оттуда. Таким образом отражается тот факт,
что ни к одной из работ нельзя приступить прежде, чем будут выполнены все работы, предшествующие ей согласно
технологии реализации проекта. Начало этого процесса — вершина без входящих, а окончание — вершина без
исходящих дуг. Остальные вершины должны иметь и те, и другие дуги.

33.

Этот метод используется, когда для операции сложно задать и определить точную
длительность.
Особенность метода PERT заключается в возможности учета вероятностного характера
продолжительностей всех или некоторых работ при расчете параметров времени на сетевой
модели. Он позволяет определять вероятности окончания проекта в заданные периоды
времени и к заданным срокам.
Вместо одной детерминированной величины продолжительности для работ проекта задаются
три оценки длительности:
оптимистическая (работа не может быть выполнена быстрее, чем за tа);
пессимистическая (работа не может быть выполнена медленнее, чем за tb);
наиболее вероятная tn
Затем вероятностная сетевая модель превращается в детерминированную путем замены трех
оценок продолжительностей каждой из работ одной величиной, называемой ожидаемой
продолжительностью tожид и рассчитываемой как средневзвешенное арифметическое трех
экспертных оценок длительностей данной работы:
tожид=( tа + tb + tn)/6
Определяется критический путь на основании для каждой tожидоперации.
Определяется среднее квадратичное отклонение каждой операции:
Ϭt=( tа + ta) /6
Среднее квадратичное отклонение времени реализации всего проекта:
Ϭпр=√∑ϬtІ

34.

Метод графической оценки и анализа (GERT, анг. Graphical Evaluation and Review
Technique) — альтернативный вероятностный метод сетевого планирования, применяется в
случаях организации работ, когда последующие задачи могут начинаться после
завершения только некоторого числа из предшествующих задач, причём не все задачи,
представленные на сетевой модели, должны быть выполнены для завершения проекта.
Разработан в США в 1966 году.
Основу применения метода GERT составляет использование альтернативных сетей,
называемых GERT-сетями. Они позволяют более адекватно задавать сложные процессы
строительного производства в тех случаях, когда затруднительно или невозможно (по
объективным причинам) однозначно определить, какие именно работы и в какой
последовательности должны быть выполнены для достижения цели проекта (то есть
существует многовариантность реализации проекта).
Расчёт GERT-сетей, моделирующих реальные процессы, чрезвычайно сложен, однако
программное обеспечение для вычисления сетевых моделей такого типа в настоящее
время не распространено.

35.

1) Правило последовательности изображения работ: сетевые модели следует строить от
начала к окончанию, т.е. слева направо.
2) Правило изображения стрелок. В сетевом графике стрелки, обозначающие работы,
ожидания или зависимости, могут иметь различный наклон и длину, но должны идти
слева направо.
3) Правило пересечения стрелок. При построении сетевого графика следует избегать
пересечения стрелок: чем меньше пересечений, тем нагляднее график.
4) Правило обозначения работ. В сетевом графике между обозначениями двух смежных
событий может проходить только одна стрелка.
5) В сетевой модели не должно быть "тупиковых" событий, то есть событий, из которых
не выходит ни одна работа, за исключением завершающего события.
6) Правило расчленения и запараллеливания работ. При построении сетевого графика
можно начинать последующую работу, не ожидая полного завершения
предшествующей.
7) Правило запрещения замкнутых контуров (циклов, петель). В сетевой модели
недопустимо строить замкнутые контуры.
8) Правило запрещения хвостовых событий. В сетевом графике не должно быть
хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением
начального события.
9) Правило изображения поставки. В сетевом графике поставки изображаются двойным
кружком либо другим знаком, отличающимся от знака обычного события данного
графика.
13) Технологическое правило построения сетевых графиков. Для построения сетевого
графика необходимо в технологической последовательности установить:
• какие работы должны быть завершены до начала данной работы;
• какие работы должны быть начаты после завершения данной работы;
• какие работы необходимо выполнять одновременно с выполнением данной работы.
14) Правила кодирования событий сетевого графика. Для кодирования сетевых
графиков необходимо пользоваться следующими правилами.
1. Все события графика должны иметь свои собственные номера.
2. Кодировать события необходимо числами натурального ряда без пропусков.
3. Номер последующему событию следует присваивать после присвоения номеров
предшествующим событиям.
4. Стрелка (работа) должна быть всегда направлена из события с меньшим номером в
событие с большим номером

36.

Наиболее распространенными направлениями
применения сетевого планирования являются:
целевые научно-исследовательские и
проектно-конструкторские разработки
сложных объектов, машин и установок, в
создании которых принимают участие многие
предприятия и организации;
планирование и управление основной
деятельностью разрабатывающих
организаций;
планирование комплекса работ по подготовке
и освоению производства новых видов
промышленной продукции;
строительство и монтаж объектов
промышленного, культурно-бытового и
жилищного назначения;
реконструкция и ремонт действующих
промышленных и других объектов;
планирование подготовки и переподготовки
кадров, проверка исполнения принятых
решений, организация комплексной проверки
деятельности предприятий, объединений,
строительно-монтажных организаций и
учреждений.