Похожие презентации:
Особенности подготовки школьников к ЕГЭ по математике (профильный уровень)
1.
Особенности подготовки школьниковк ЕГЭ по математике
(профильный уровень)
2.
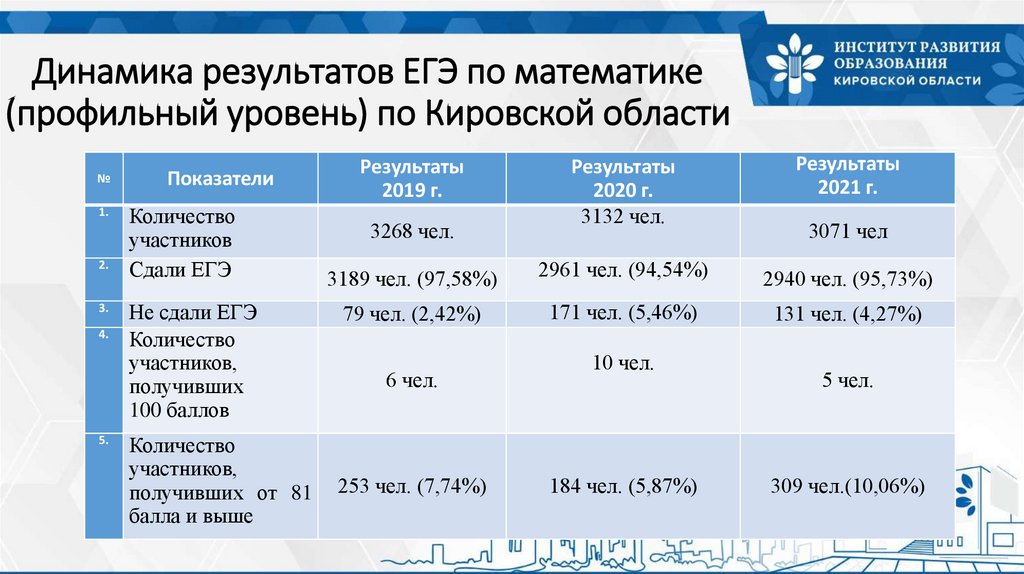
Динамика результатов ЕГЭ по математике(профильный уровень) по Кировской области
№
1.
2.
3.
4.
5.
Показатели
Количество
участников
Сдали ЕГЭ
Не сдали ЕГЭ
Количество
участников,
получивших
100 баллов
Количество
участников,
получивших от 81
балла и выше
Результаты
2020 г.
3132 чел.
Результаты
2021 г.
3189 чел. (97,58%)
2961 чел. (94,54%)
2940 чел. (95,73%)
79 чел. (2,42%)
171 чел. (5,46%)
131 чел. (4,27%)
Результаты
2019 г.
3268 чел.
6 чел.
253 чел. (7,74%)
10 чел.
184 чел. (5,87%)
3071 чел
5 чел.
309 чел.(10,06%)
3.
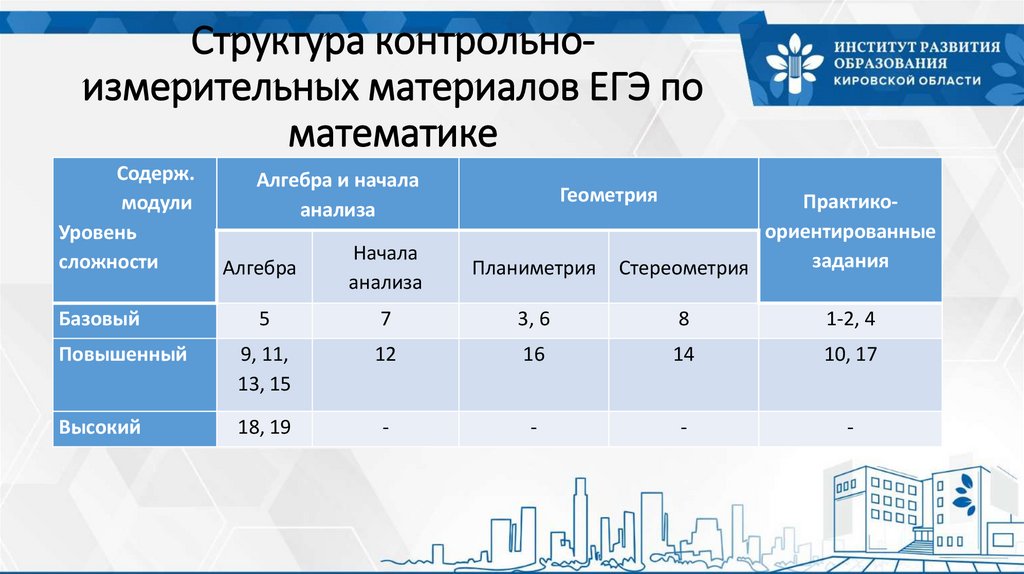
Структура контрольноизмерительных материалов ЕГЭ поматематике
Содерж.
модули
Уровень
сложности
Алгебра и начала
анализа
Геометрия
Практикоориентированные
задания
Стереометрия
Алгебра
Начала
анализа
Планиметрия
5
7
3, 6
8
1-2, 4
Повышенный
9, 11,
13, 15
12
16
14
10, 17
Высокий
18, 19
-
-
-
-
Базовый
4.
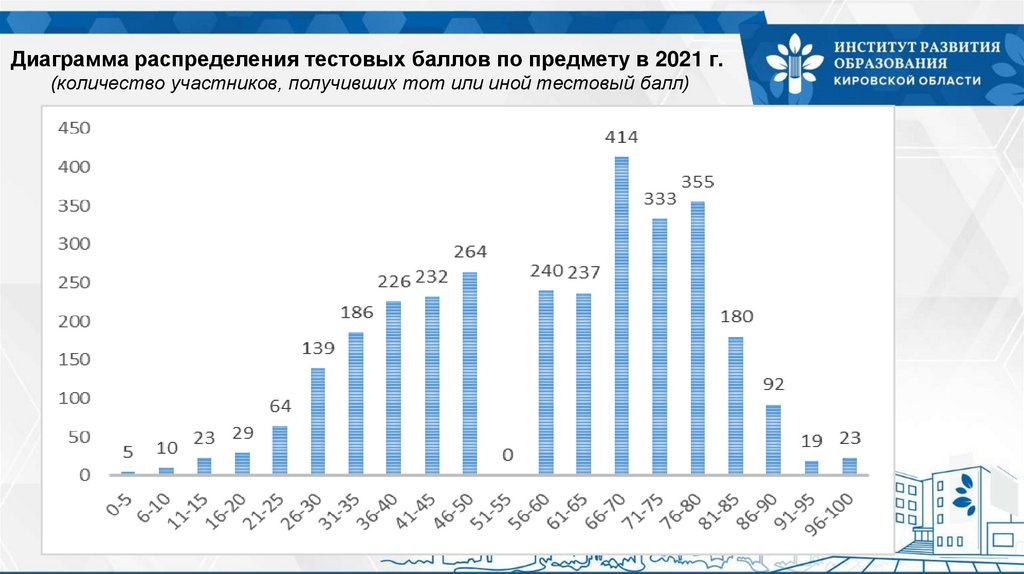
Диаграмма распределения тестовых баллов по предмету в 2021 г.(количество участников, получивших тот или иной тестовый балл)
5.
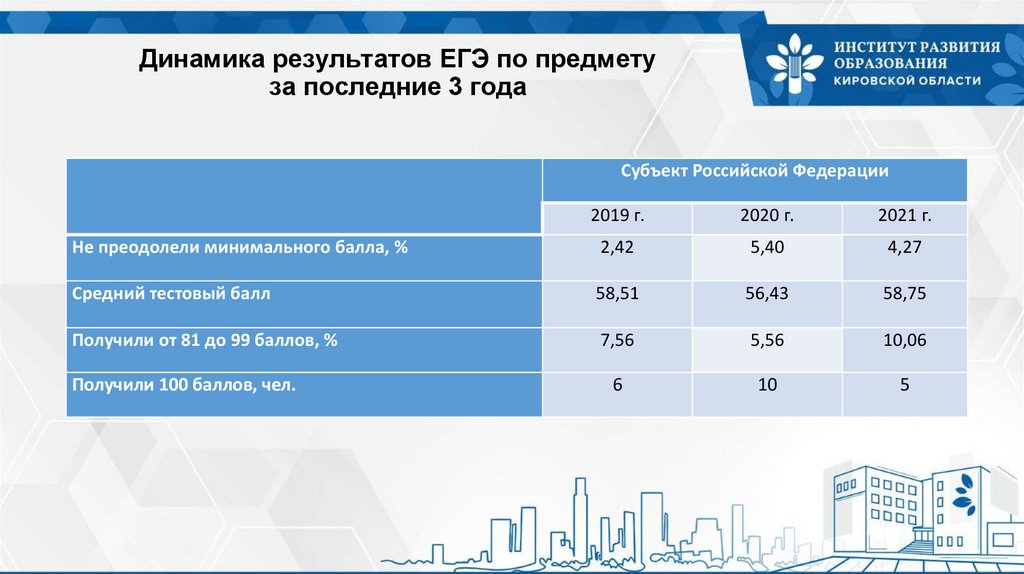
Динамика результатов ЕГЭ по предметуза последние 3 года
Субъект Российской Федерации
2019 г.
2020 г.
2021 г.
Не преодолели минимального балла, %
2,42
5,40
4,27
Средний тестовый балл
58,51
56,43
58,75
Получили от 81 до 99 баллов, %
7,56
5,56
10,06
6
10
5
Получили 100 баллов, чел.
6.
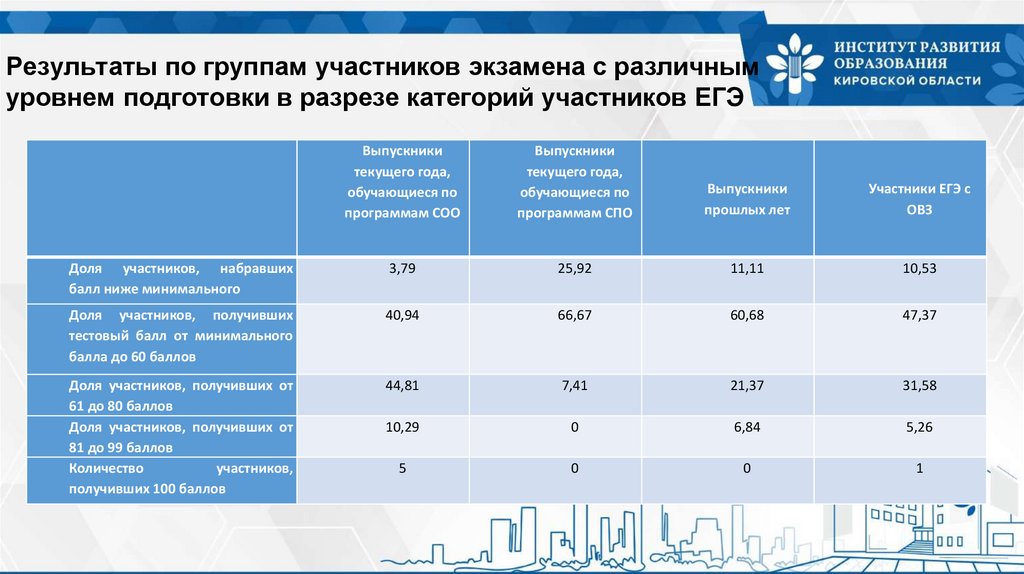
Результаты по группам участников экзамена с различнымуровнем подготовки в разрезе категорий участников ЕГЭ
Выпускники
текущего года,
обучающиеся по
программам СОО
Выпускники
текущего года,
обучающиеся по
программам СПО
Выпускники
прошлых лет
Участники ЕГЭ с
ОВЗ
Доля участников, набравших
балл ниже минимального
3,79
25,92
11,11
10,53
Доля участников, получивших
тестовый балл от минимального
балла до 60 баллов
40,94
66,67
60,68
47,37
Доля участников, получивших от
61 до 80 баллов
Доля участников, получивших от
81 до 99 баллов
Количество
участников,
получивших 100 баллов
44,81
7,41
21,37
31,58
10,29
0
6,84
5,26
5
0
0
1
7.
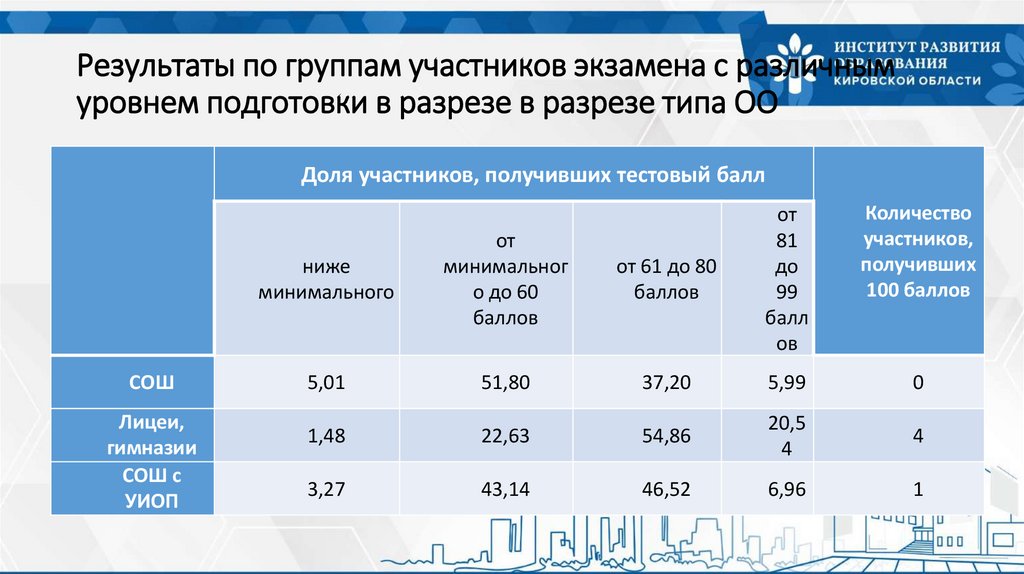
Результаты по группам участников экзамена с различнымуровнем подготовки в разрезе в разрезе типа ОО
Доля участников, получивших тестовый балл
СОШ
Лицеи,
гимназии
СОШ с
УИОП
Количество
участников,
получивших
100 баллов
ниже
минимального
от
минимальног
о до 60
баллов
от 61 до 80
баллов
от
81
до
99
балл
ов
5,01
51,80
37,20
5,99
0
1,48
22,63
54,86
20,5
4
4
3,27
43,14
46,52
6,96
1
8.
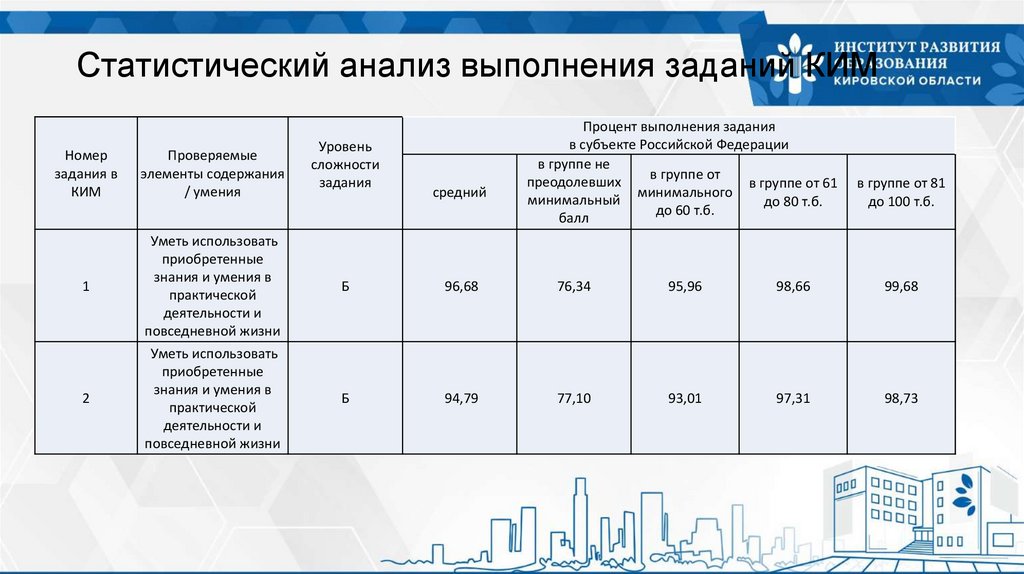
Статистический анализ выполнения заданий КИМНомер
задания в
КИМ
1
2
Проверяемые
элементы содержания
/ умения
Уметь использовать
приобретенные
знания и умения в
практической
деятельности и
повседневной жизни
Уметь использовать
приобретенные
знания и умения в
практической
деятельности и
повседневной жизни
Уровень
сложности
задания
средний
Процент выполнения задания
в субъекте Российской Федерации
в группе не
в группе от
преодолевших
в группе от 61
минимального
минимальный
до 80 т.б.
до
60
т.б.
балл
в группе от 81
до 100 т.б.
Б
96,68
76,34
95,96
98,66
99,68
Б
94,79
77,10
93,01
97,31
98,73
9.
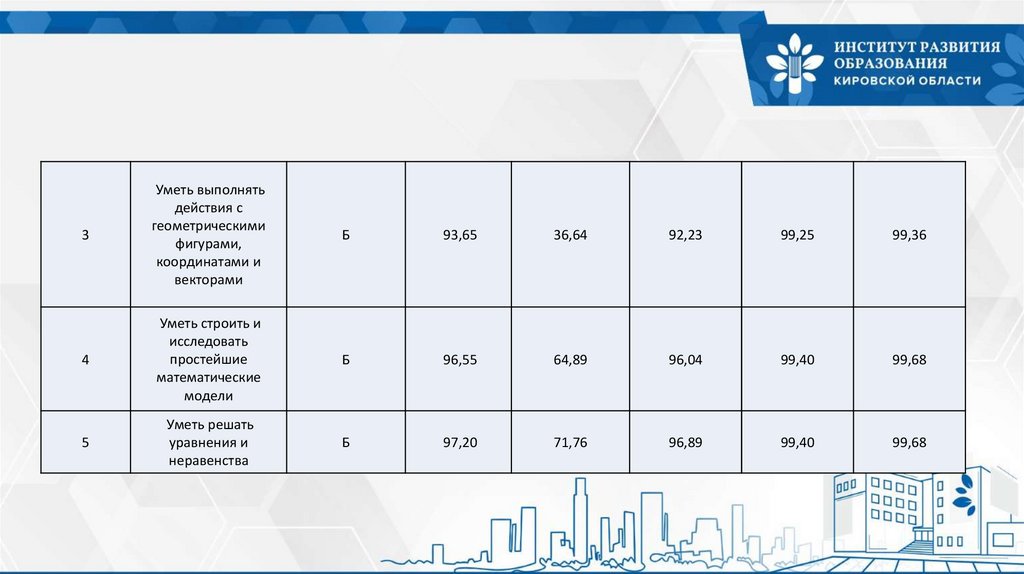
3Уметь выполнять
действия с
геометрическими
фигурами,
координатами и
векторами
Б
93,65
36,64
92,23
99,25
99,36
4
Уметь строить и
исследовать
простейшие
математические
модели
Б
96,55
64,89
96,04
99,40
99,68
5
Уметь решать
уравнения и
неравенства
Б
97,20
71,76
96,89
99,40
99,68
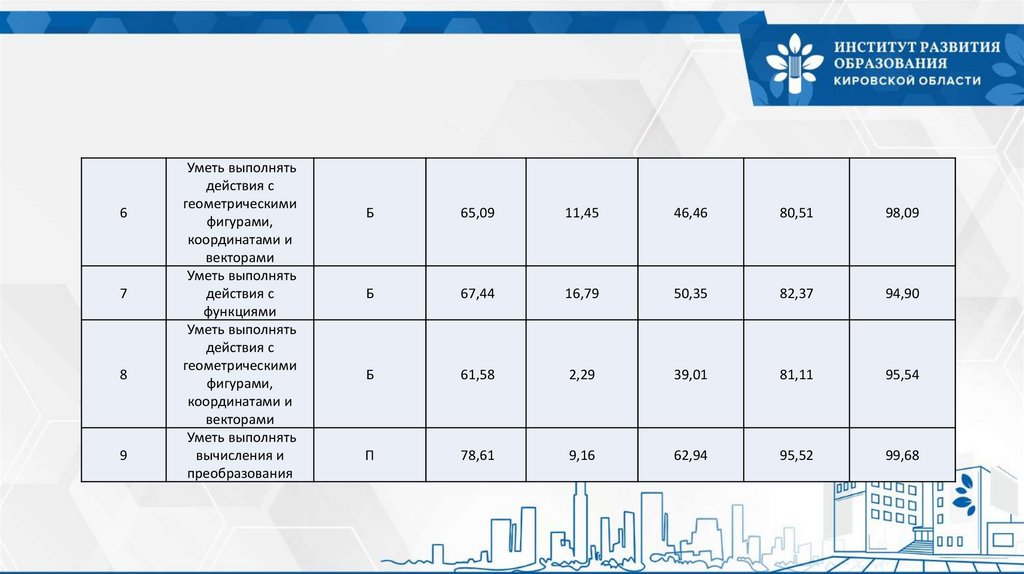
10.
67
8
9
Уметь выполнять
действия с
геометрическими
фигурами,
координатами и
векторами
Уметь выполнять
действия с
функциями
Уметь выполнять
действия с
геометрическими
фигурами,
координатами и
векторами
Уметь выполнять
вычисления и
преобразования
Б
65,09
11,45
46,46
80,51
98,09
Б
67,44
16,79
50,35
82,37
94,90
Б
61,58
2,29
39,01
81,11
95,54
П
78,61
9,16
62,94
95,52
99,68
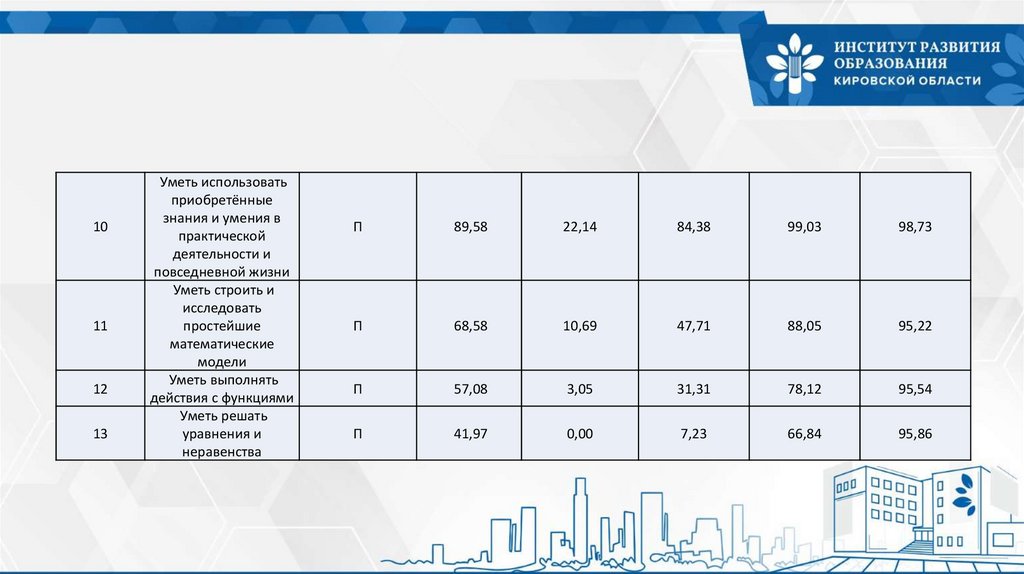
11.
1011
12
13
Уметь использовать
приобретённые
знания и умения в
практической
деятельности и
повседневной жизни
Уметь строить и
исследовать
простейшие
математические
модели
Уметь выполнять
действия с функциями
Уметь решать
уравнения и
неравенства
П
89,58
22,14
84,38
99,03
98,73
П
68,58
10,69
47,71
88,05
95,22
П
57,08
3,05
31,31
78,12
95,54
П
41,97
0,00
7,23
66,84
95,86
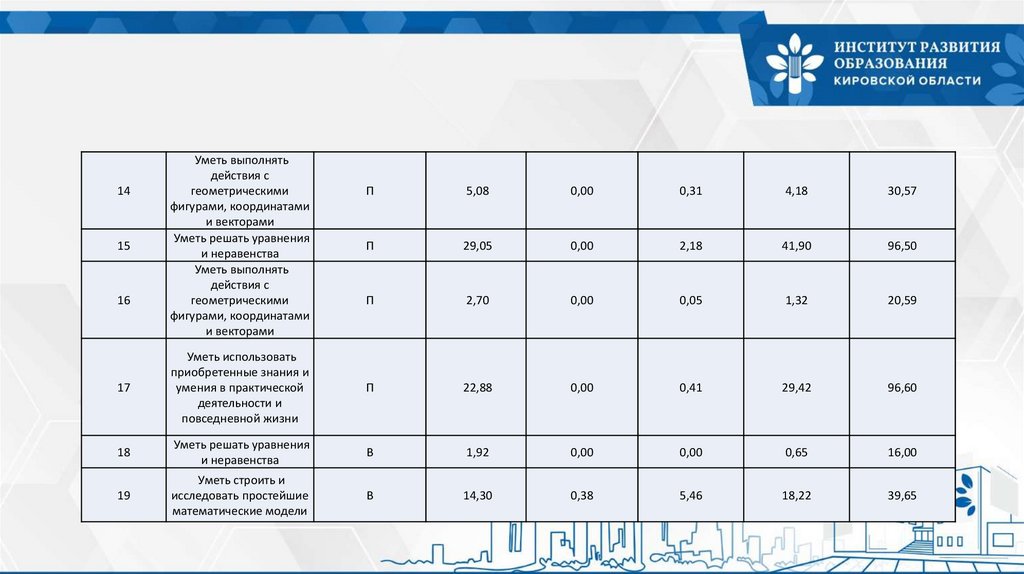
12.
14Уметь выполнять
действия с
геометрическими
фигурами, координатами
и векторами
Уметь решать уравнения
и неравенства
Уметь выполнять
действия с
геометрическими
фигурами, координатами
и векторами
П
5,08
0,00
0,31
4,18
30,57
П
29,05
0,00
2,18
41,90
96,50
П
2,70
0,00
0,05
1,32
20,59
17
Уметь использовать
приобретенные знания и
умения в практической
деятельности и
повседневной жизни
П
22,88
0,00
0,41
29,42
96,60
18
Уметь решать уравнения
и неравенства
В
1,92
0,00
0,00
0,65
16,00
19
Уметь строить и
исследовать простейшие
математические модели
В
14,30
0,38
5,46
18,22
39,65
15
16
13.
Выводы по итогам анализа выполнения заданий поматематике (профильный уровень) в 2021 году
- Умение использовать приобретенные знания и умения в практической
деятельности и повседневной жизни, умения строить и исследовать
простейшие математические модели, умение решать уравнения и
неравенства, умение выполнять действия с геометрическими фигурами,
координатами и векторами, умения выполнять действия с функциями на
базовом уровне сформированы достаточно хорошо.
- Умение выполнять вычисления и преобразования, умение использовать
приобретенные знания и умения в практической деятельности и
повседневной жизни на повышенном уровне сформированы достаточно
хорошо. Умения выполнять действия с функциями на повышенном уровне
сформировано достаточно.
- Нельзя назвать стабильными и сформированными на высоком уровне
умения выполнять действия с функциями (задача 12). Здесь результативность
во многом зависит от техники дифференцирования.
14.
Выводы по итогам анализа выполнения заданий поматематике (профильный уровень) в 2021 году
- Умение решать уравнения и неравенства на повышенном уровне
(задача 13) сформировано недостаточно. Требует внимания обучение
решению простейших тригонометрических уравнений и обоснованию
отбора корней уравнения на указанном промежутке.
- Традиционной в 2021 году остается проблема формирования умения
выполнять действия с геометрическими фигурами, координатами и
векторами у обучающихся на повышенном уровне. Даже, если этот
показатель зависит от задачи, решаемость не поднимается выше 9%. В
2021 году средний процент выполнения заданий по региону составил
около 5%.
- Требует особого внимания обучение школьников методу подстановки
при решении неравенств. Умение решать уравнения и неравенства на
повышенном уровне (задача 15) сформировано недостаточно.
15.
Рекомендации по совершенствованию организации и методикипреподавания предмета в на основе выявленных типичных затруднений
и ошибок по совершенствованию преподавания учебного предмета всем
обучающимся
- при анализе КИМ 2021 года было выявлено, что в части с кратким ответом достаточно
большое количество ошибок были допущены из-за вычислительных ошибок. Таким образом,
необходимо продолжать развивать вычислительные навыки учащихся на уроках, строго
запрещать использование калькуляторов при работе на уроках алгебры и геометрии; помимо
вычислительных навыков, следует особое внимание уделить рациональным способам
вычислений;
- при подготовке к ЕГЭ 2022 года, следует уходить от «натаскивания» на определенные типы
задач: учащиеся в недостаточной мере уделяют внимание вдумчивому смысловому чтению
задач с выделением важных элементов;
- обратить внимание учащихся, на необходимость работы с КИМом (подчеркивать важные
элементы, выделять вопрос, делать дополнительные построения);
- особое внимание необходимо обратить на важность обоснованного отбора корней
уравнения при решении №13. Необходимо использовать различные способы отбора, в том
числе графическую иллюстрацию отрезка, на котором необходимо отобрать корни. При этом,
если корни отбираются путем подстановки значений n, помимо нахождения значений, при
котором корни лежат в заданном отрезке, необходимо указать и те, значения, при которых
корни впервые выходят за границы отрезка. Это считается необходимым обоснованием того,
что других корней в заданном отрезке не существует;
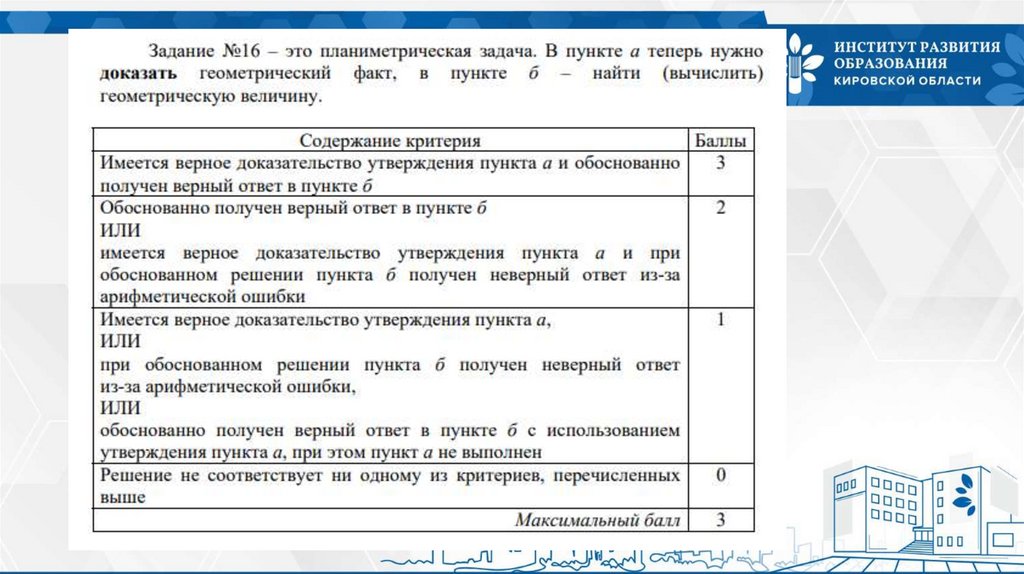
16.
- при решении задания № 14 обратить внимание на обоснование соответствияпостроенных сечений условию задачи;
- необходимо продолжать работу с доказательством геометрических
утверждений (задания 14 и 16). Учащиеся должны быть обучены выстраивать
утверждения при доказательстве таким образом, чтобы каждое последующее
прямо следовало из предыдущего до полного оказательства;
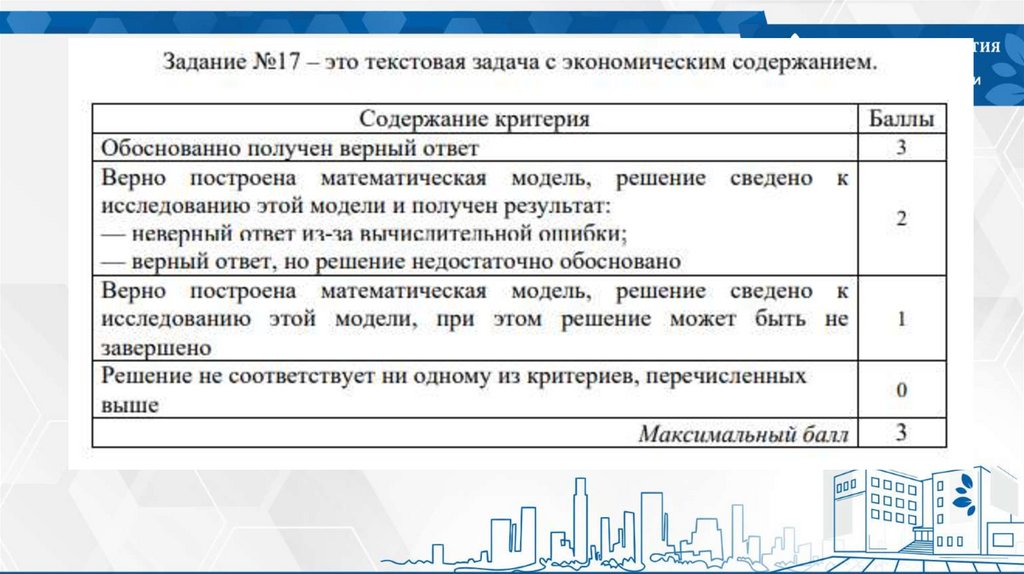
- при решении задания №17 особое внимание уделить обоснованности
построения математической модели;
- периодически организовывать уроки обобщающего повторения пройденного
материала за курс геометрии, алгебры и начал анализа, это позволит
актуализировать полученные ранее знания. Особенно это касается некоторых
нечасто используемых формул и свойств при решении геометрических задач;
17.
- необходимо, в обязательном порядке, проводить анализ демонстрационноговарианта ЕГЭ 2022 года по математике. Это позволит учителям и учащимся иметь
представление об уровне трудности и типах заданий предстоящей экзаменационной
работы;
- использование материалов открытого банка заданий, опубликованных на
официальном сайте ФИПИ, даст возможность подготовиться качественно к экзамену
и на уроках с помощью учителя, и самостоятельно дома каждому выпускнику;
- использование ресурсов, компилирующих варианты заданий на основе открытого
банка заданий ФИПИ, а также других источников, для более разносторонней
подготовки к ЕГЭ по математике;
- подготовку к ЕГЭ по математике профильного уровня сложности не рекомендуется
начинать с решения готовых вариантов. В первую очередь необходимо разобраться с
теоретической базой, а также спектром прототипов по каждому из заданий. Когда
этот материал будет достаточно усвоен, приступать к решению вариантов целиком;
18.
- образовательным учреждениям рекомендуется проводитьпробные экзамены с соблюдением всех требований реального ЕГЭ
по математике, с периодичностью, не допускающей перегрузки
учеников. Это позволит, помимо оценки возможностей каждого из
учащихся, сформировать стрессоустойчивость к реальному
экзамену ЕГЭ. В частности, необходимо внедрение эффективных
механизмов текущего и рубежного контроля (проведение
диагностических и тренировочных работ в системе Статград).
19.
20.
Ошибки учащихся при решении №1321.
Ошибки учащихся при решении №1322.
Ошибки учащихся при решении №1323.
Ошибки учащихся при решении №1324.
Ошибки учащихся при решении №1325.
26.
Ошибки учащихся при решении №1427.
Ошибки учащихся при решении №1428.
Типичные ошибки учащихся при решении№14
29.
30.
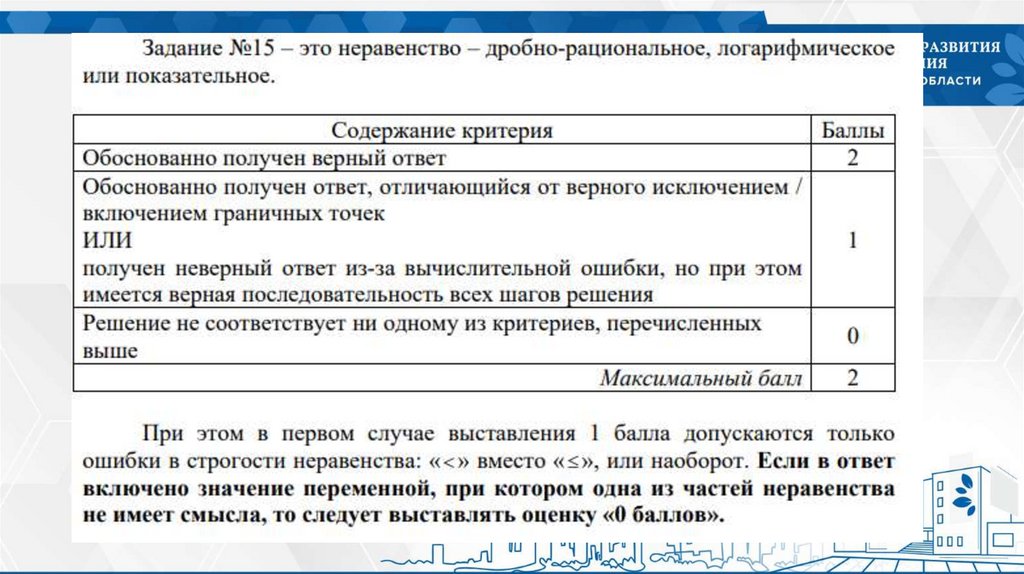
Ошибки учащихся при решении №1531.
Ошибки учащихся при решении №1532.
Ошибки учащихся при решении №1533.
34.
Ошибки учащихся при решении №1635.
Ошибки учащихся при решении №1636.
37.
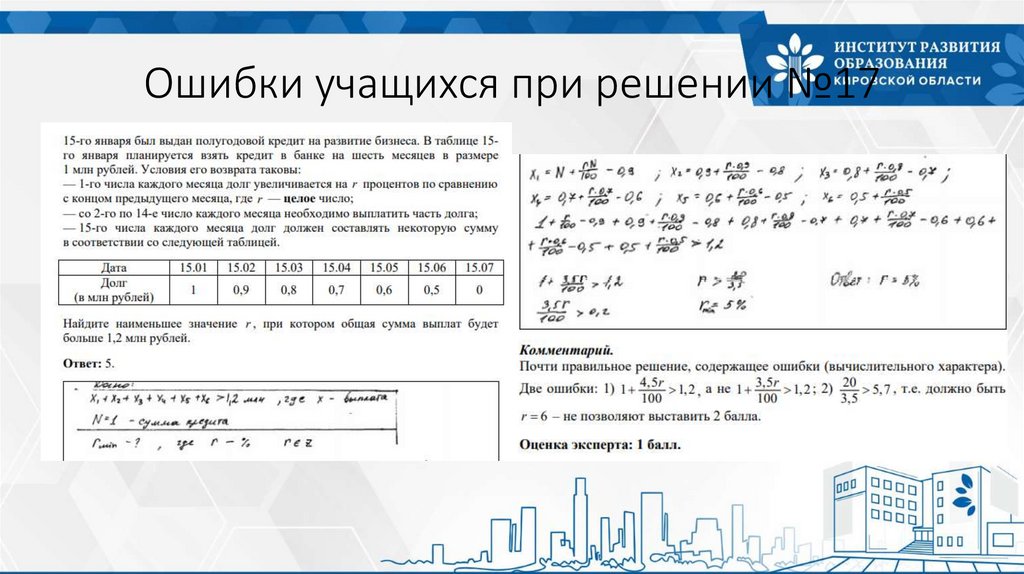
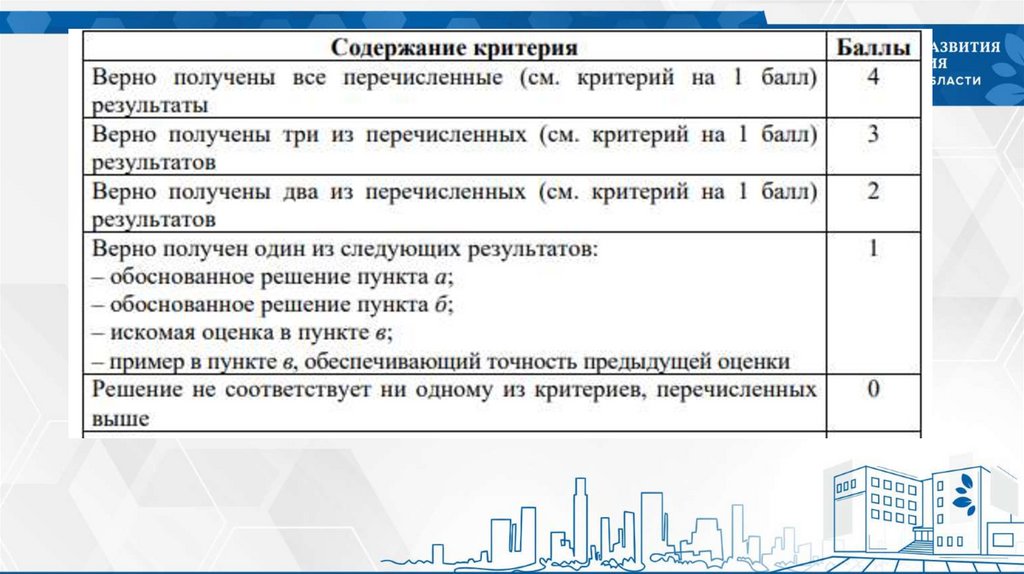
Ошибки учащихся при решении №1738.
Ошибки учащихся при решении №1739.
40.
41.
Ошибки учащихся при решении №1842.
Ошибки учащихся при решении №1843.
44.
45.
Ошибки учащихся при решении №1946.
Ошибки учащихся при решении №1947.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы ФИПИ (сайт https://fipi.ru)
48.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы федерального портала «Российское образование»
(http://www.edu.ru)
49.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы «Навигатора ГИА» Рособрнадзора (http://navgia.obrnadzor.gov.ru/navigator-gia/materialy-dlya-podgotovki-k-ege/)
50.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы «Открытого банка задач ЕГЭ по математике»
(https://prof.mathege.ru/)
51.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы сайта https://alexlarin.net/ege21.html
52.
Ресурсно-методическое обеспечение подготовкишкольников к ЕГЭ по математике (профильный уровень)
• Материалы сайта https://ege.sdamgia.ru/


































 Математика
Математика








