Похожие презентации:
Универсальность дискретного (цифрового) представления информации
1.
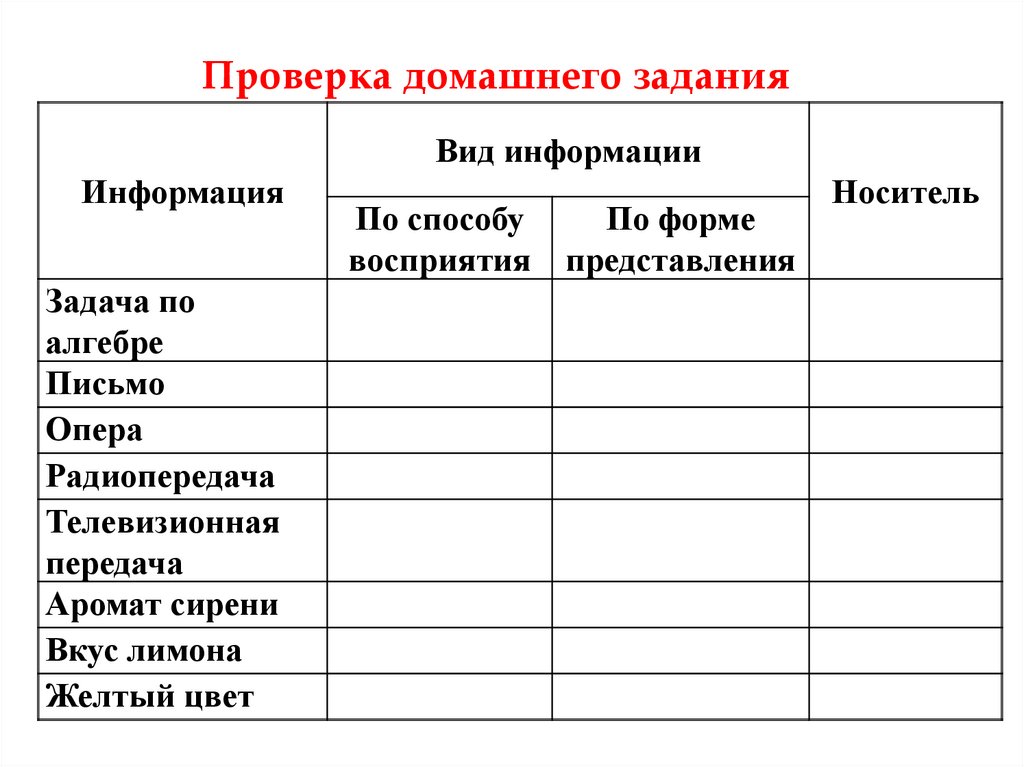
Проверка домашнего заданияВид информации
Информация
Задача по
алгебре
Письмо
Опера
Радиопередача
Телевизионная
передача
Аромат сирени
Вкус лимона
Желтый цвет
По способу
восприятия
По форме
представления
Носитель
2.
• Тема урока:Универсальность дискретного
(цифрового) представления
информации.
Дискретизация — это преобразование
непрерывных изображений и звука в набор
дискретных значений в форме кодов.
3.
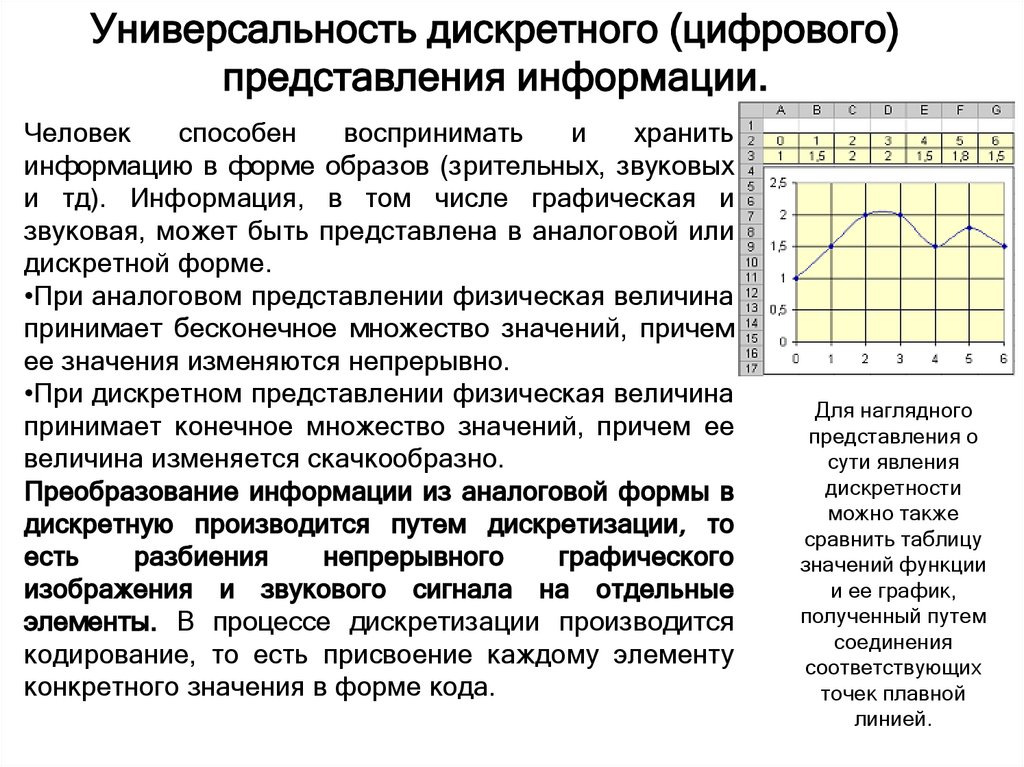
Универсальность дискретного (цифрового)представления информации.
Человек
способен
воспринимать
и
хранить
информацию в форме образов (зрительных, звуковых
и тд). Информация, в том числе графическая и
звуковая, может быть представлена в аналоговой или
дискретной форме.
•При аналоговом представлении физическая величина
принимает бесконечное множество значений, причем
ее значения изменяются непрерывно.
•При дискретном представлении физическая величина
принимает конечное множество значений, причем ее
величина изменяется скачкообразно.
Преобразование информации из аналоговой формы в
дискретную производится путем дискретизации, то
есть
разбиения
непрерывного
графического
изображения и звукового сигнала на отдельные
элементы. В процессе дискретизации производится
кодирование, то есть присвоение каждому элементу
конкретного значения в форме кода.
Для наглядного
представления о
сути явления
дискретности
можно также
сравнить таблицу
значений функции
и ее график,
полученный путем
соединения
соответствующих
точек плавной
линией.
4.
Универсальность дискретного (цифрового)представления информации.
Достоинства дискретного (цифрового) представления
информации:
• простота;
• удобство физической реализации;
•универсальность
представления
любого
вида
информации;
•обеспечение защиты от случайных искажений или
нежелательного доступа.
Компьютер способен хранить только дискретно
представленную информацию тк его память состоит из
отдельных битов.
5.
Преобразование информации происходит впроцессе кодирования информации.
Код – правило для преобразования одного набора
знаков в другой.
Кодирование – процесс преобразования одного набора
знаков в другой.
Длина кода – количество знаков, которое используется
для представления кодируемого символа.
6.
Измерение информацииВ качестве длины кода для кодирования одного
символа в ПК выбрано 8бит=1байт.
1
0
1
1
1
1
0
1
Различных комбинаций 0 и 1 при длине кода 8 бит
может быть 28=256, поэтому с помощью одной
таблицы перекодировки можно закодировать 256
символов. При длине кода в 2 байта (16 бит) можно
закодировать 65536 символов.
Бит – одна из двух цифр 0 или 1 в машинном коде.
Каждый символ кодируется 8 или 16 битным кодом.
1 байт=8 бит
1 Кбайт = 210байт=1024байт
1 Мбайт = 210Кбайт = 220байт
1 Гбайт = 210Мбайт = 220Кбайт = 230байт
7.
Кодирование текстовой информацииВ качестве международного стандарта принята кодовая
таблица ASCII (American Standard Code for Information
Interchange).
• Коды 0-32 – соответствуют операциям (перевод
строки, ввод пробела и т. д.).
• Коды 33-127 - соответствуют символам латинского
алфавита,
цифрам,
знакам
арифметических
операций и препинания.
• Коды
128-255
–
соответствуют
символам
национального алфавита.
8.
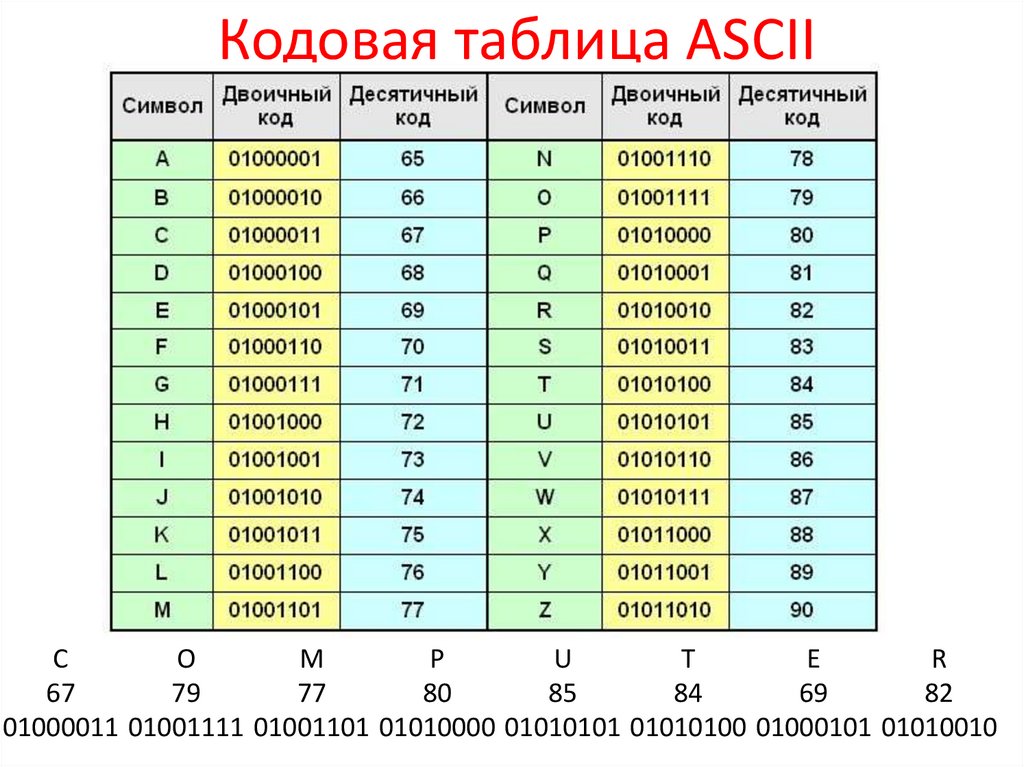
Кодовая таблица ASCIIC
O
M
P
U
T
E
R
67
79
77
80
85
84
69
82
01000011 01001111 01001101 01010000 01010101 01010100 01000101 01010010
9.
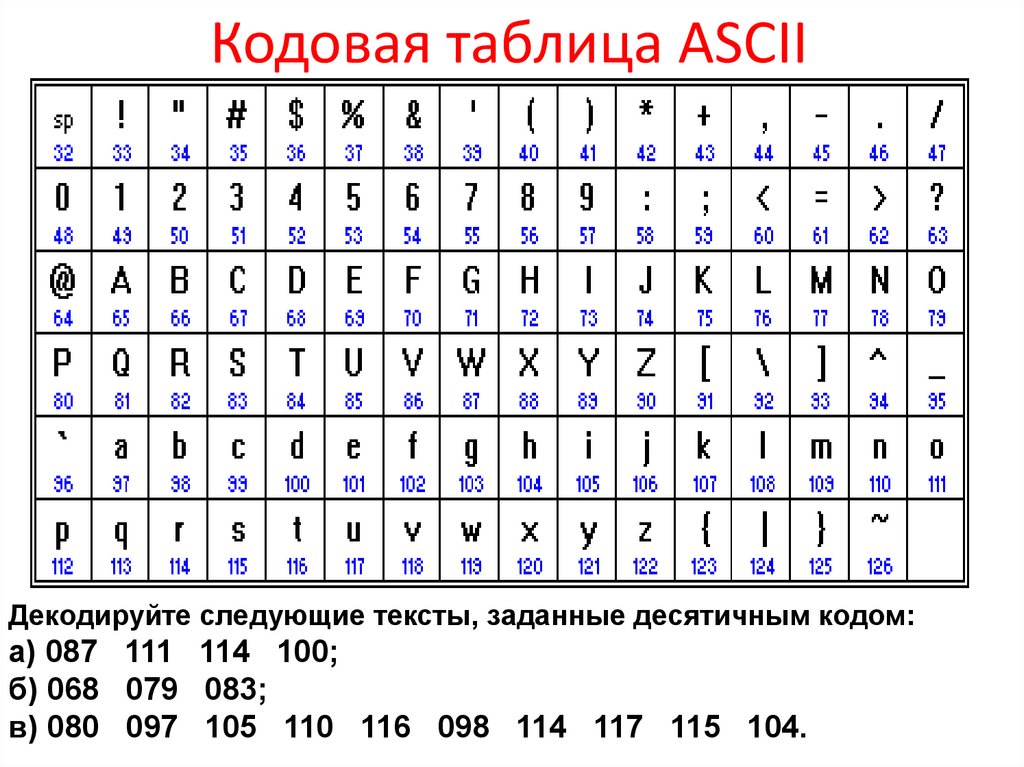
Кодовая таблица ASCIIДекодируйте следующие тексты, заданные десятичным кодом:
а) 087 111 114 100;
б) 068 079 083;
в) 080 097 105 110 116 098 114 117 115 104.
10.
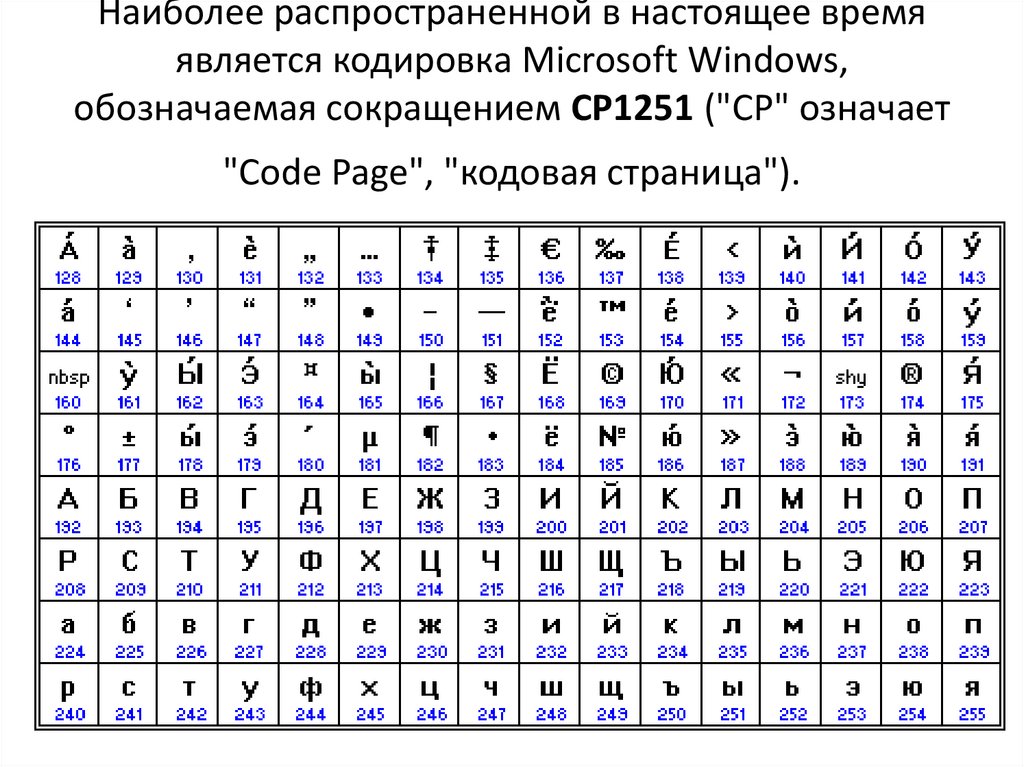
Наиболее распространенной в настоящее времяявляется кодировка Microsoft Windows,
обозначаемая сокращением CP1251 ("CP" означает
"Code Page", "кодовая страница").
11.
Компьютеры фирмы Apple, работающие подуправлением операционной системы Mac OS,
используют свою собственную кодировку Mac.
12.
Кодирование графической информации• Графическая информация на экране монитора дискретна и
представляется в виде растрового изображения: из точек –
ПИКСЕЛЕЙ. Связана она с техническими особенностями
устройства экрана. Количество пикселей на экране зависит от
разрешения экрана 800х600, 1024х768 и т.п. Экран монитора
характеризуется такими параметрами как длина диагонали
(в дюймах) и разрешающая способность (в точках на дюйм,
dpi).
Пиксели бывают только трех
цветов - зеленого, синего и
красного. Другие цвета
образовываются при помощи
смешения цветов.
Рассмотрим самый простой
случай - каждый кусочек
пикселя может либо гореть
(1), либо не гореть (0).
Из трех цветов можно получить
восемь комбинаций.
13.
• Для получения богатой палитры цветов базовым цветам могут бытьзаданы различные интенсивности. Цветные изображения могут
иметь различную глубину цвета, которая задается
количеством битов, используемым для кодирования цвета
точки. Наиболее распространенными значениями глубины
цвета являются 8, 16, 24 или 32 бита.
Качество двоичного кодирования изображения
определяется разрешающей способностью экрана и
глубиной цвета.
14.
Объем видеопамяти• Для того чтобы на экране монитора формировалось
изображение, информация о каждой его точке (код цвета
точки) должна храниться в видеопамяти компьютера.
• Рассчитаем необходимый объем видеопамяти для одного
из графических режимов, например, с разрешением
800 х 600 точек и глубиной цвета 24 бита на точку.
Всего точек на экране: 800 • 600 = 480 000
Необходимый объем видеопамяти:
24 бит • 480 000 = 11 520 000 бит = 1 440 000 байт =
1406,25 Кбайт = 1,37 Мбайт.
15.
Векторная графикаГрафическая информация может быть представлена в
виде векторного изображения.
Векторное
изображение
представляет
собой
графический объект, состоящий из элементарных
отрезков и дуг.
Положение этих элементарных объектов определяется
координатами точек и длиной радиуса. Для каждой
линии указывается ее тип (сплошная, пунктирная,
штрих-пунктирная), толщина и цвет. Информация о
векторном изображении кодируется как обычная
буквенно-цифровая и обрабатывается специальными
программами.
16.
Кодирование числовой информацииДля записи информации о количестве объектов
используются числа. Числа записываются с
использованием особых знаковых систем, которые
называются системами счисления. Алфавит
системы счисления состоит из символов, которые
называются цифрами.
Системы счисления
Цифры – это символы, участвующие в записи чисел
и составляющие некоторый алфавит.
Число – это некоторая величина.
Система счисления (СС) – это способ записи
чисел с помощью цифр.
17.
Виды систем счисленияПозиционной
называется такая СС, в
которой
количественный
эквивалент («вес»)
цифры зависит от ее
месторасположения в
записи числа.
Непозиционной
называется такая система
счисления, у которой
количественный эквивалент
(«вес») цифры не зависит
от ее местоположения в
записи числа.
123 руб.- 321 руб.
Примеры: двоичная СС, Примеры: единичная
десятичная СС.
СС, древнеегипетская
СС, римская СС,
алфавитные СС.
18.
Непозиционные ССНепозиционные СС возникли раньше позиционных.
Последние являются в свою очередь результатом
длительного исторического развития непозиционных
СС.
Непозиционной называется такая система
счисления, у которой количественный эквивалент
(«вес») цифры не зависит от ее местоположения в
записи числа.
К непозиционным системам счисления относятся
единичная система счисления, древнеегипетская
десятичная
непозиционная
СС,
римская
СС,
алфавитные системы счисления.
19.
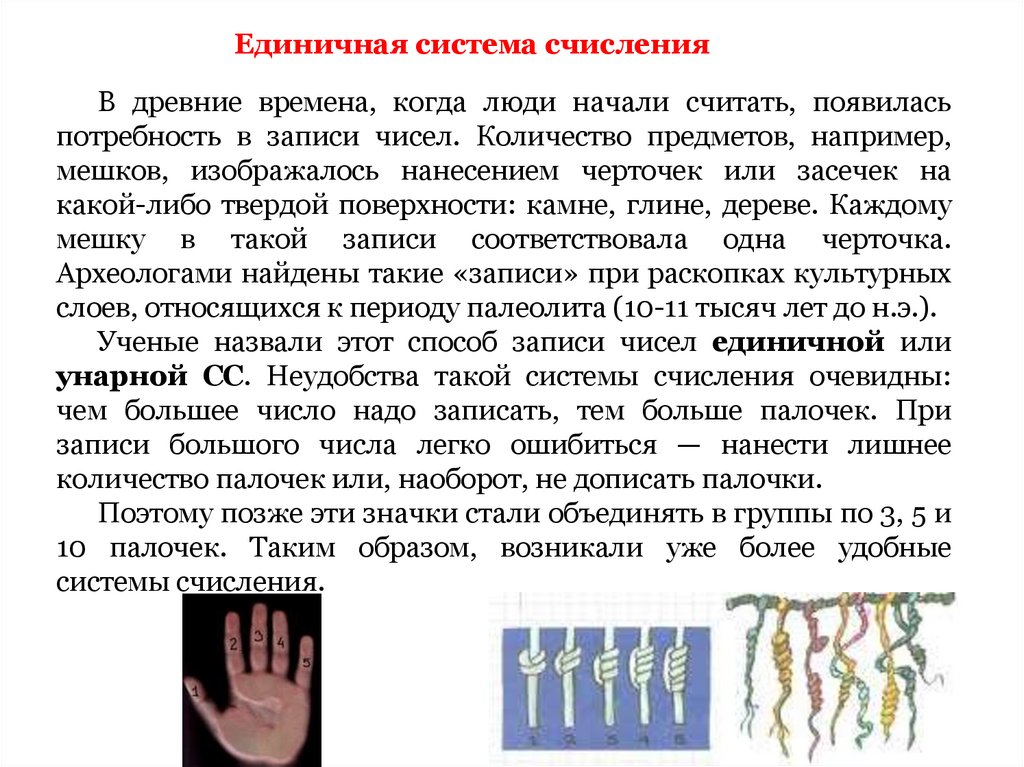
Единичная система счисленияВ древние времена, когда люди начали считать, появилась
потребность в записи чисел. Количество предметов, например,
мешков, изображалось нанесением черточек или засечек на
какой-либо твердой поверхности: камне, глине, дереве. Каждому
мешку в такой записи соответствовала одна черточка.
Археологами найдены такие «записи» при раскопках культурных
слоев, относящихся к периоду палеолита (10-11 тысяч лет до н.э.).
Ученые назвали этот способ записи чисел единичной или
унарной СС. Неудобства такой системы счисления очевидны:
чем большее число надо записать, тем больше палочек. При
записи большого числа легко ошибиться — нанести лишнее
количество палочек или, наоборот, не дописать палочки.
Поэтому позже эти значки стали объединять в группы по 3, 5 и
10 палочек. Таким образом, возникали уже более удобные
системы счисления.
20.
Древнеегипетскаядесятичная непозиционная система счисления
Древнеегипетская десятичная непозиционная система возникла во второй половине третьего тысячелетия до н.э. Бумагу заменяла глиняная дощечка, и именно поэтому цифры имеют такое начертание.
В этой системе счисления использовали в качестве цифр ключевые
числа 1, 10, 100, 1000 и т.д. и записывались они при помощи специальных
иероглифов.
Какое число изображено?
21.
Римская система счисленияВ римской системе счисления для обозначения цифр использовались
следующие латинские буквы:
I- 1, V-5, Х- 10, L-50, С- 100, D-500, М- 1000
Правила составления чисел в римской системе счисления:
Число равно:
1. Сумме значений идущих подряд нескольких одинаковых «цифр»
(назовем их группой первого вида);
2. Разности значений двух «цифр», если слева от большей«цифры» стоит
меньшая. В этом случае от значения большей «цифры» отнимается
значение меньшей «цифры». Вместе они образуют группу второго вида.
Заметим, что левая «цифра» может быть меньше правой максимум на один
порядок: так перед L(50) и С( 100) из «младших» может стоять только Х(10),
перед D(500) и М(1000) — только С(100), перед V(5)- только I(1);
3. Сумме значений групп и «цифр», не вошедших в группы первого или
второго вида.
22.
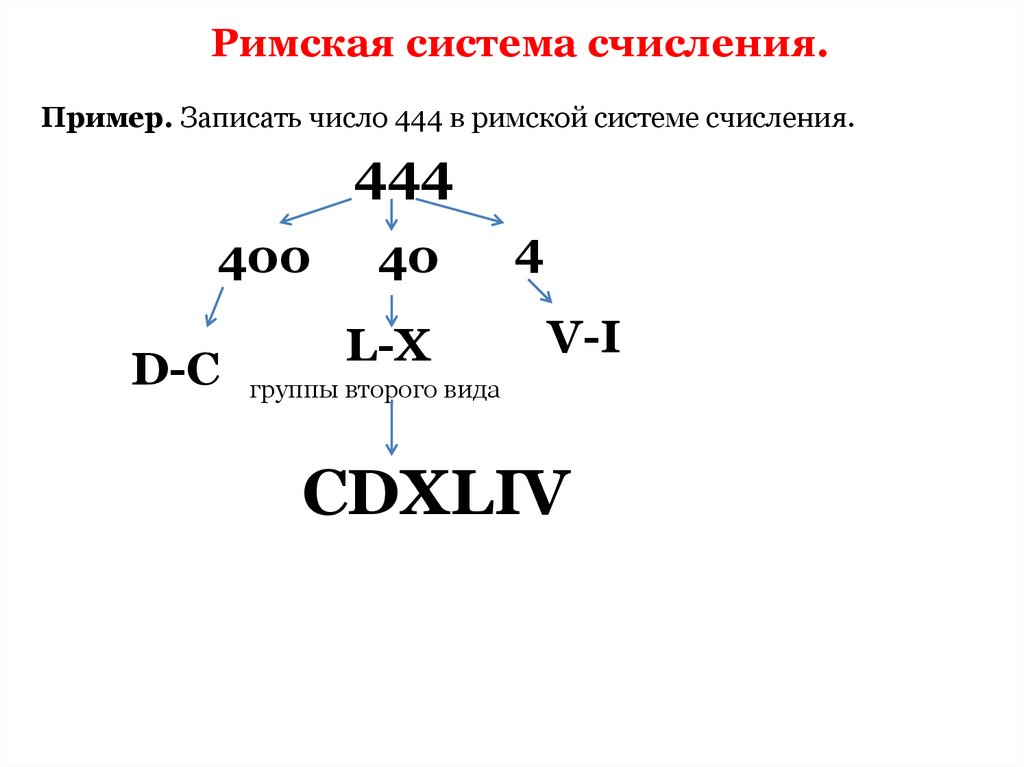
Римская система счисления.Пример. Записать число 444 в римской системе счисления.
444
400
D-C
40
L-X
4
V-I
группы второго вида
CDXLIV
23.
Позиционные ССПозиционной называется такая СС, в которой
количественный эквивалент («вес») цифры зависит от
ее месторасположения в записи числа.
Пример. Рассмотрим число 222
В записи этого числа используются трижды цифра 2. На вклад каждой
цифры в величину числа разный. Первая 2 означает число сотен, вторая –
число десятков, третья – число единиц.
Если сравнить вес каждой цифры в этом числе, то получиться что
первая 2 «больше» второй в десять раз и т.д.
Разряд – это позиция цифры в числе.
Основание (базис) позиционной СС – это
количество цифр и других знаков, используемых для
записи чисел в данной СС.
24.
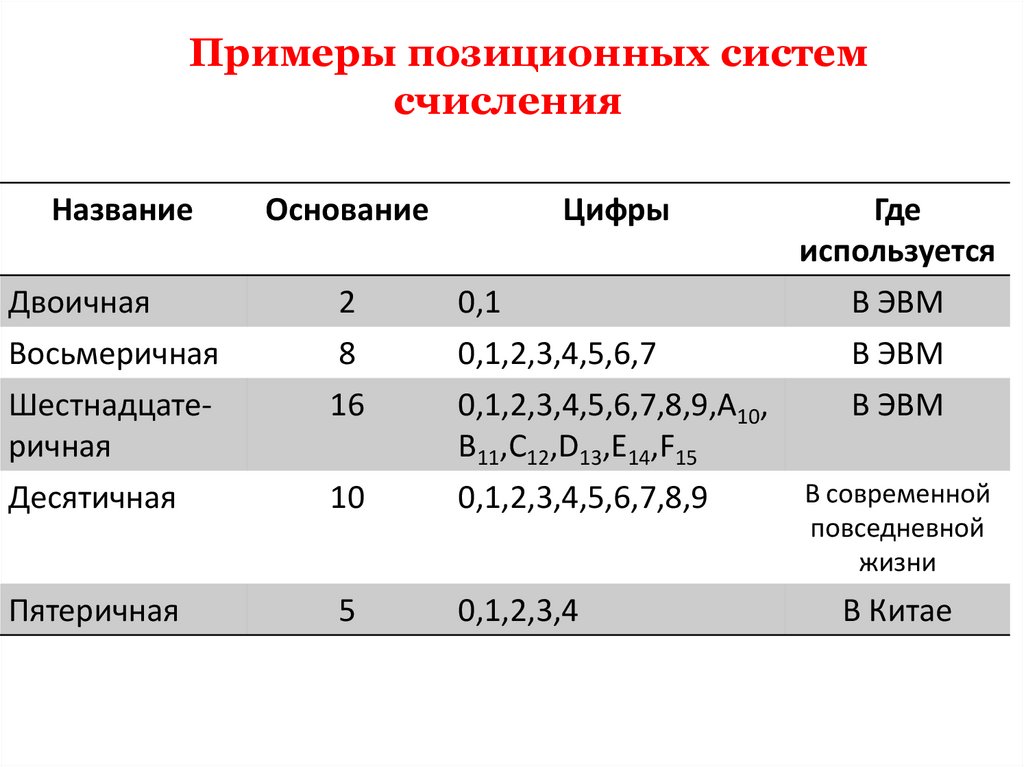
Примеры позиционных системсчисления
Название
Основание
Цифры
Где
используется
Двоичная
Восьмеричная
Шестнадцатеричная
Десятичная
2
8
16
В ЭВМ
В ЭВМ
В ЭВМ
10
0,1
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7,8,9,A10,
B11,C12,D13,E14,F15
0,1,2,3,4,5,6,7,8,9
Пятеричная
5
0,1,2,3,4
В современной
повседневной
жизни
В Китае
25.
Двоичная система счисления• Двоичное
кодирование
–
один
из
распространенных
способов
представления
информации. Двоичный алфавит состоит из двух
цифр 0 и 1.
• Цифровые
ЭВМ
(персональные
компьютеры
относятся к классу цифровых) используют двоичное
кодирование любой информации. В основном это
объясняется тем, что построить техническое
устройство, безошибочно различающее 2 разных
состояния сигнала, технически оказалось проще, чем
то, которое бы безошибочно различало 5 или 10
различных состояний.
26.
Двоичная система счисления• Двоичная система счисления аналогична десятичной
за исключением того, что в формировании числа
участвуют всего лишь две знака-цифры: 0 и 1. Как
только разряд достигает своего предела (т.е.
единицы), появляется новый разряд, а старый
обнуляется.
• Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
27.
Двоичная система счисленияВ десятичной системе счисления любое число можно
представить в форме суммы единиц, десяток, сотен и
т.д.
3210
разряды
147610 = 1000 + 400 + 70 + 6= 1 * 103 + 4 * 102 +
+7 * 101 + 6 * 100
Аналогично можно разложить двоичное число.
765 4 3 210
разряды
100010012 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 +
+0*22 + 0*21 + 1*20=128+0+0+0+8+0+0+1=13710
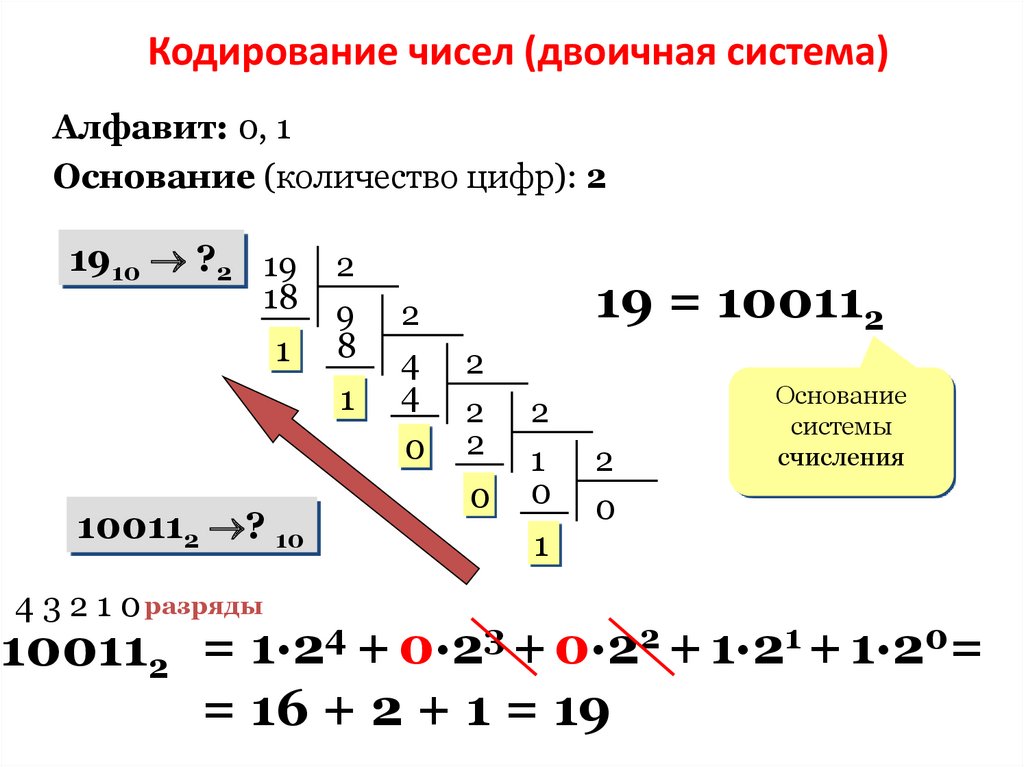
28.
Кодирование чисел (двоичная система)Алфавит: 0, 1
Основание (количество цифр): 2
1910 ?2 19
18
1
2
9
8
1
2
4
4
0
100112 ? 10
4 3 2 1 0 разряды
19 = 100112
2
2
2
0
2
1
0
1
2
0
Основание
системы
счисления
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20=
= 16 + 2 + 1 = 19
29.
Перевод десятичного числа в двоичное• Один из способов – это целочисленное деление на два и
формирование двоичного числа из остатков.
7710 ?2
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе,
начиная с конца: 1001101.
7710 = 10011012
• Проверим:
10011012 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 +
+1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77 10
30.
Вопросы:• Заполните в тетради таблицу слайд № 1.
• Почему дискретное представление информации универсально?
• Почему в вычислительной технике широко используется
двоичное кодирование?
• Определение понятий: код, кодирование, длина кода, Понятие
байта и бита.
• Принцип кодирование текстовой информации.
• Принцип кодирование графической информации.
• Определение понятия «система счисления». Виды СС.
Приведите примеры различных видов.
• Как осуществить перевод числа в двоичной системе в число
десятичной СС?
• Как осуществить перевод числа в десятичной системе в число
двоичной СС?
Домашнее задание:
Выполнить самостоятельную работу №3 (по вариантам)





















 Информатика
Информатика








