Спецглавы высшей математики. Лекционный материал

1.

Спецглавы высшей
математики
лекционный материал (1)
Лектор: Давыденко Александр Юрьевич,
д. ф.-м.н., профессор

2.

Цель и задачи курса
Цель курса: изучение математического аппарата,
используемого в геолого-геофизических приложениях.
Задачи:
1. Изучить основы вероятностно-статистических методов
анализа геолого-геофизической информации;
2. Освоить методы аппроксимации экспериментальных
данных;
3. Изучить применение численных методов
дифференцирования и интегрирования при решении
прямых задач геофизики.
4. Освоить применение специализированного
математического пакета Маткад15 для решения
прикладных задач.
2

3.

Литература
• Дэвис Дж. Статистический анализ данных в геологии. В 2-х
томах., М., «Недра», 1990 г.
• Вентцель Е., Овчаров Л. - Теория вероятностей и ее
инженерные приложения. М., Высшая школа, 2000.
• Дубровская Л.И., Князев Г.Б., Компьютерная обработка
естественно-научных данных методами многомерной
прикладной статистики: Учебное пособие. –Томск: ТМЛПресс, 2011,- 120 с.
• Никитин А. А, Петров А. В. «Теоретические основы
обработки геофизической информации» уч. пособие,
Москва, Изд-во РГГУ, 2008, 112 стр.
• Демьянов В. В. , Савельева Е. А. Геостатистика
• теория и практика. М., Наука, 2010.
• Интернет-ресурсы.
3

4.

Вероятностно-статистические
методы в геофизике
Методы прикладной геофизики располагают обширным арсеналом программно-аппаратных средств для
получения, извлечения, анализа и отображения геологических данных.
Значительный объем информации, ее многомерный характер, наличие случайных помех естественного и
антропогенного происхождения порождает проблемы извлечения полезной информации из полученных
полевых данных. Существенную роль при этом играют вероятностно- статистические методы обработки и
анализа данных.
Математическая статистика - раздел математики, разрабатывающий методы регистрации, описания и анализа
данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных
явлений.
Методы математической статистики широко используются в самых различных областях: экономика (эконометрика);
медицинская статистик; биология; метеорология и …
Геостати́ стика — это наука занимающаяся анализом, обработкой и представлением пространственнораспределенной информации на основе статистических методов.
Как самостоятельная наука геостатистика начала развиваться из решения задач геологического
опробования (Дэвид Криг, Ж. Матерон) в середине 20-го столетия. Сейчас геостатистические методы широко
используются не только в геологии и геофизике, но и во многих других областях, имеющих дело с
пространственно-распределенными данными (метеорология, география, океанология и …).
4

5.

Задачи статистического анализа
В математической статистике (МС) фундаментальными понятиями
являются «Генеральная совокупность» и «Выборка из
генеральной совокупности» (далее просто «Выборка»).
Основные задачи МС:
• оценка параметров генеральной совокупности по выборке;
• определение доверительных интервалов оцениваемых
параметров;
• Проверка статистических гипотез о сходстве/различии
сравниваемых выборок;
В геостатистическом анализе понятие выборки расширено
за счет учета пространственного положения элементов выборки.
5

6.

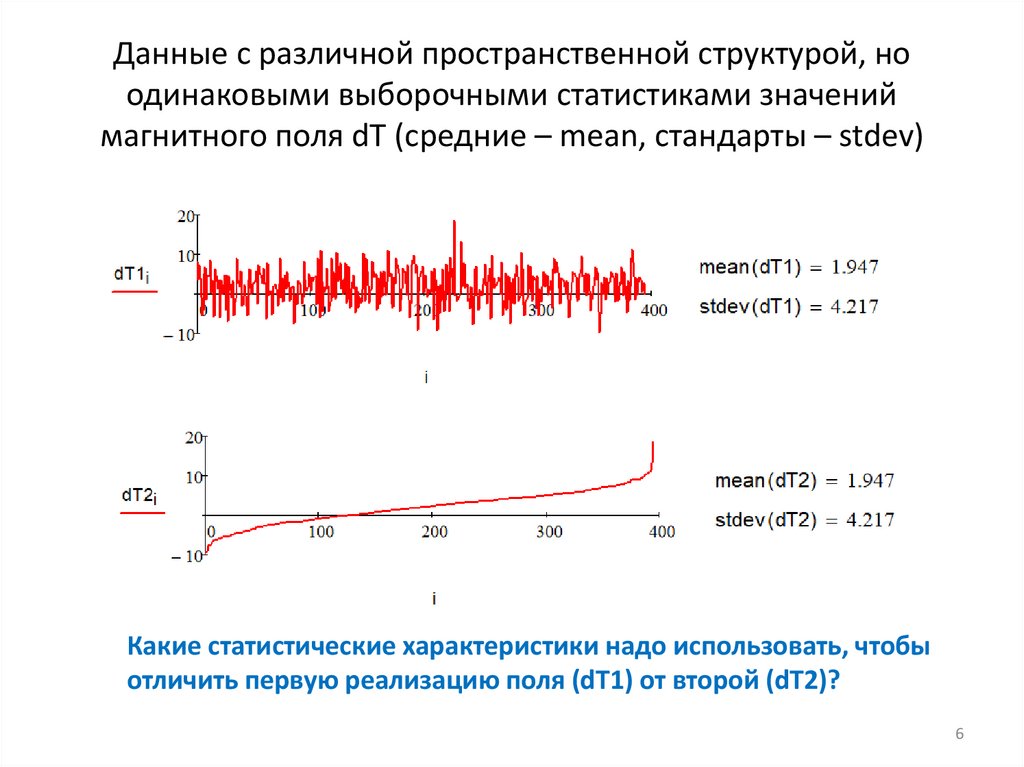
Данные с различной пространственной структурой, но
одинаковыми выборочными статистиками значений
магнитного поля dT (средние – mean, стандарты – stdev)
Какие статистические характеристики надо использовать, чтобы
отличить первую реализацию поля (dT1) от второй (dT2)?
6

7.

Применение геостатистических
методов
• Определение рациональных систем
геологического опробования при подсчете
запасов.
• Выделение элементов структуры полей и
определение их статистических характеристик
• Решение задач интерполяции и экстраполяции
полей.
• Разделение полей на составляющие.
• Проверка геостатистических гипотез.
7

8.

Литература
• Дэвис Дж. Статистический анализ данных в геологии. В 2-х томах., М.,
«Недра», 1990 г.
• Вентцель Е., Овчаров Л. - Теория вероятностей и ее инженерные
приложения. М., Высшая школа, 2000.
• Дубровская Л.И., Князев Г.Б., Компьютерная обработка естественнонаучных данных методами многомерной прикладной статистики:
Учебное пособие. –Томск: ТМЛ-Пресс, 2011,- 120 с.
• Никитин А. А, Петров А. В. «Теоретические основы обработки
геофизической информации» уч. пособие, Москва, Изд-во РГГУ, 2008,
112 стр.
• Интернет-ресурсы.
Учебная литература по пакету Маткад 15
• http://old.exponenta.ru/soft/Mathcad/Mathcad.asp и др.
• Макаров Е. Инженерные расчеты в Маткад 15
• Новиковский Е. А. Работа в MatCAD 15.
8

9.

Основы программирования в среде Mathcad 15
Mathcad — программная среда из класса систем автоматизированного
проектирования (Computer Aided Design ), позволяющая решать широкий
класс математических и специализированных инженерных, в т. ч.
геофизических задач, с использованием интуитивного и простого для
использования интерфейса.
Работа в Маткад осуществляется в пределах рабочего листа, на котором
уравнения и выражения отображаются наглядным образом в привычной
математической транскрипции.
9

10.

Ввод данных трех случайных величин x1, x2, x3 из
файла data_1.xlsx
Внимание! В начале работы файл Маткад должен
быть сохранен в той же папке, что и файл с данными
data_1.xlsx.
10

11.

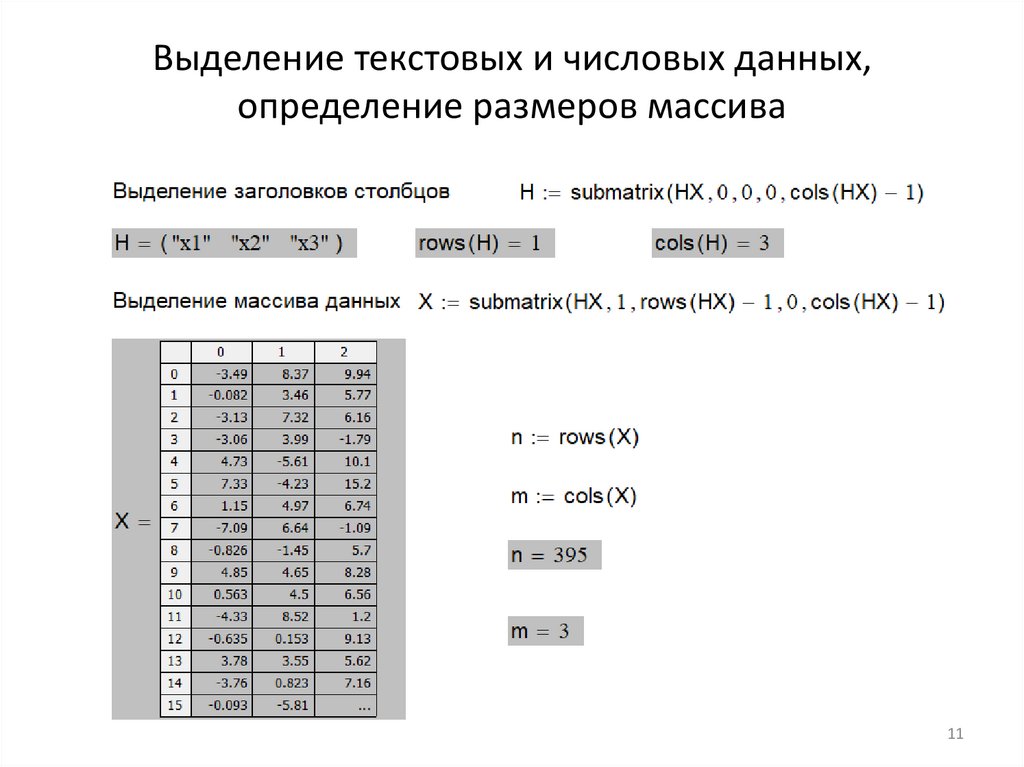
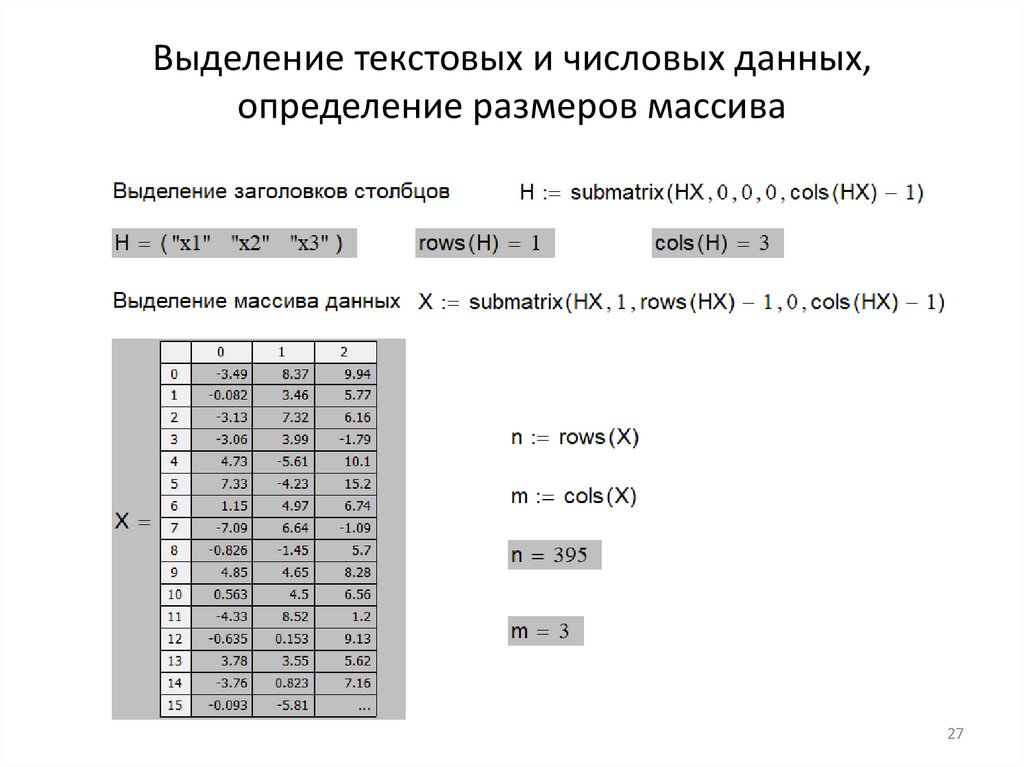
Выделение текстовых и числовых данных,
определение размеров массива
11

12.

X - система многомерных случайных величин;
x1, x2, x3 – одномерные случайные величины
12

13.

Одномерные и многомерные величины
• Столбцы таблицы, рассматриваемые по отдельности, –
выборки одномерных случайных величин. Некоторый
столбец – выборка одномерной случайной величины
• Совокупность столбцов – выборка многомерной
случайной величины, размерность которой определена
количеством столбцов.
Например, рассмотрение системы из пяти столбцов –
приводит к необходимости анализа пятимерной случайной
величины. Если столбцов 25, то каждый объект (строчка
массива) характеризуется 25-ти мерным вектором (25-ю
признаками), а все объекты надо рассматривать в 25-ти
мерном пространстве признаков.
13

14.

Одномерные статистики для переменных x1, x2, x3
14

15.

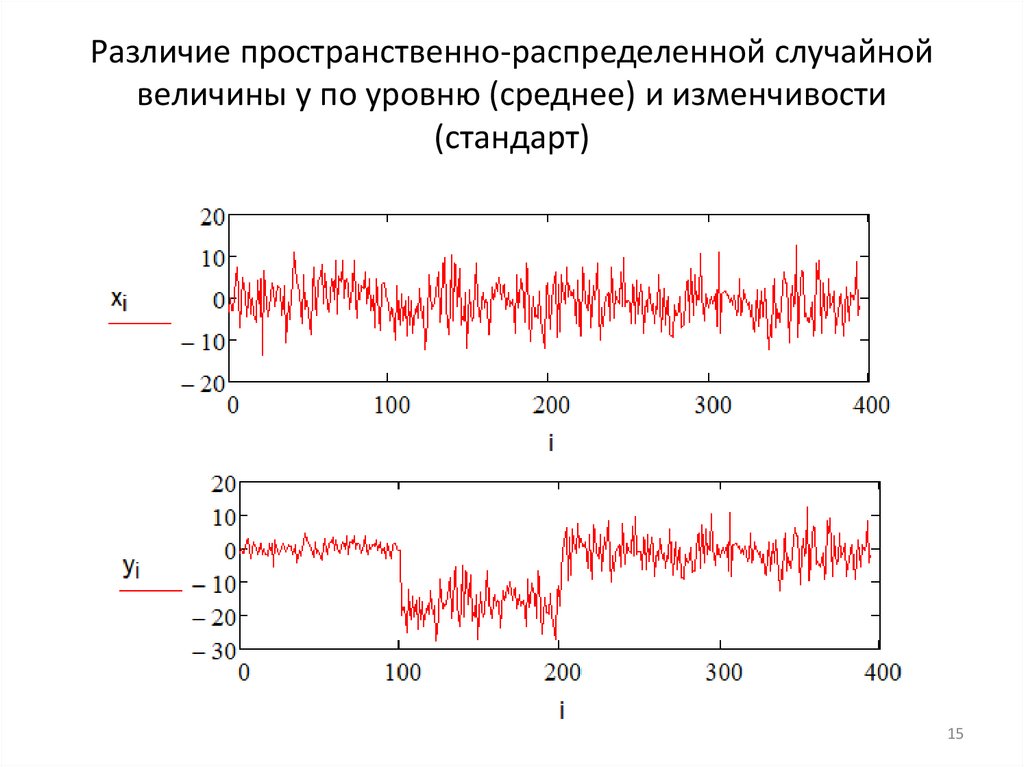
Различие пространственно-распределенной случайной
величины y по уровню (среднее) и изменчивости
(стандарт)
15

16.

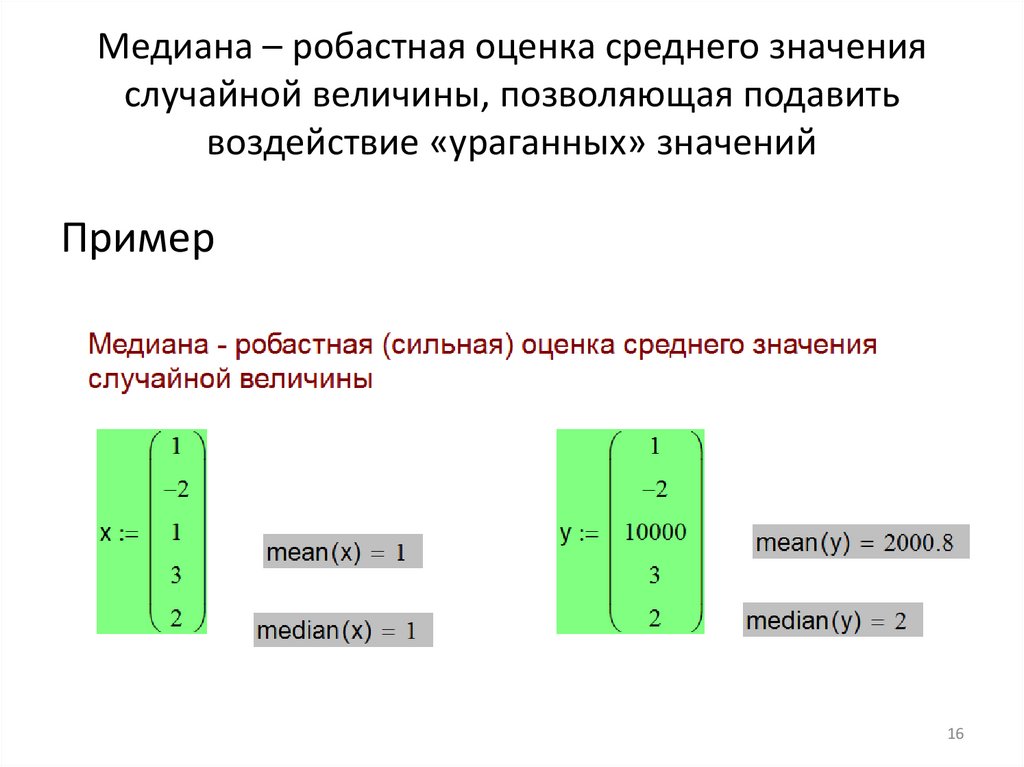
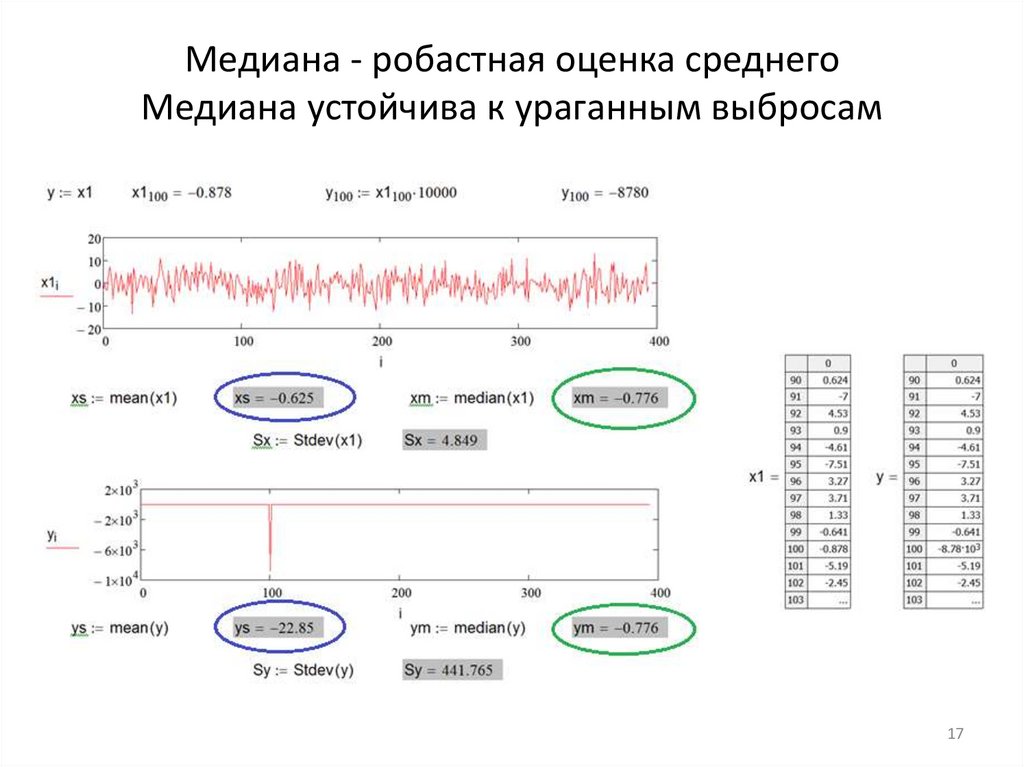
Медиана – робастная оценка среднего значения
случайной величины, позволяющая подавить
воздействие «ураганных» значений
Пример
16

17.

Медиана - робастная оценка среднего
Медиана устойчива к ураганным выбросам
17

18.

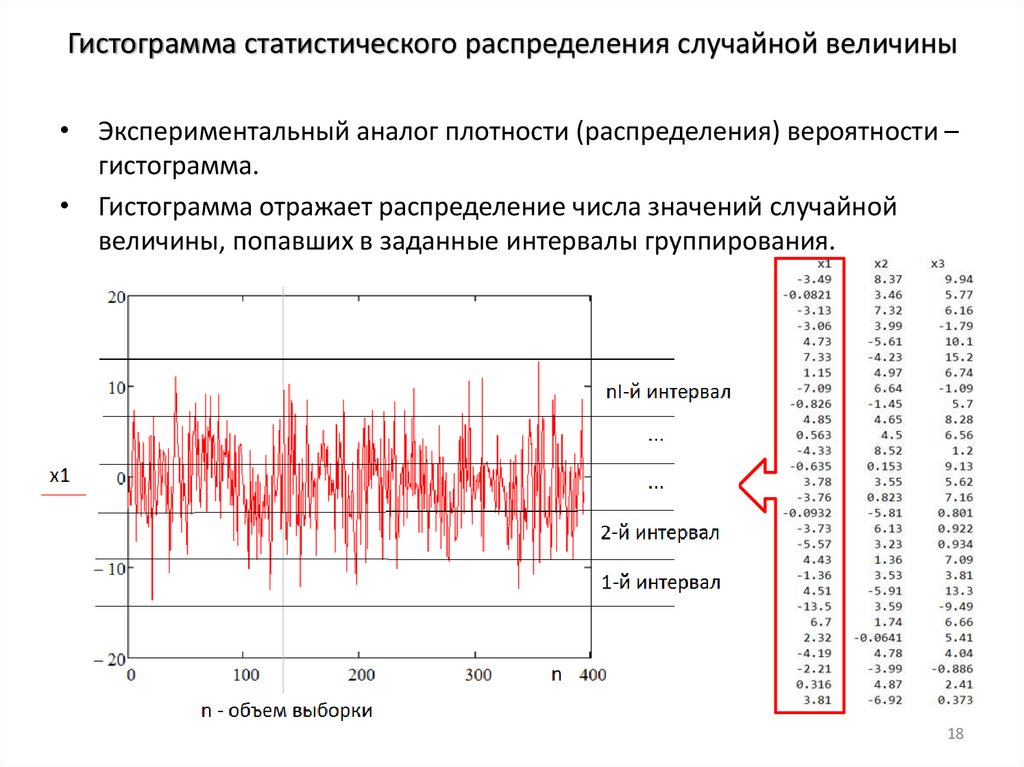
Гистограмма статистического распределения случайной величины
• Экспериментальный аналог плотности (распределения) вероятности –
гистограмма.
• Гистограмма отражает распределение числа значений случайной
величины, попавших в заданные интервалы группирования.
18

19.

Гистограмма статистического
распределения случайной величины
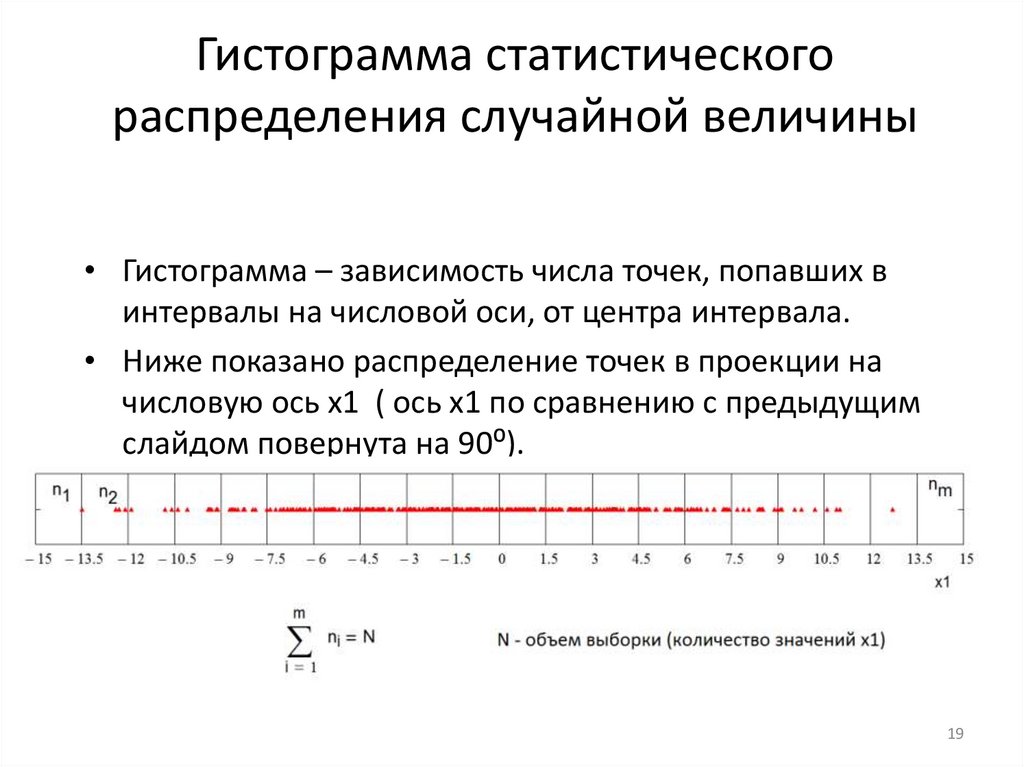
• Гистограмма – зависимость числа точек, попавших в
интервалы на числовой оси, от центра интервала.
• Ниже показано распределение точек в проекции на
числовую ось x1 ( ось x1 по сравнению с предыдущим
слайдом повернута на 90⁰).
19

20.

20

21.

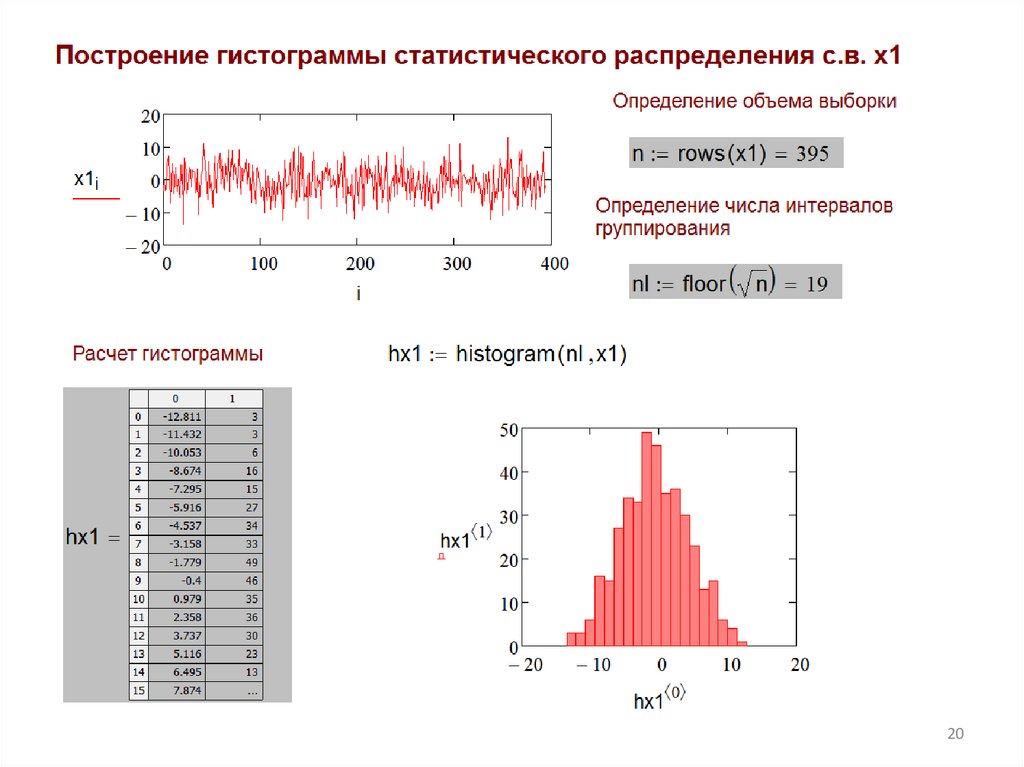
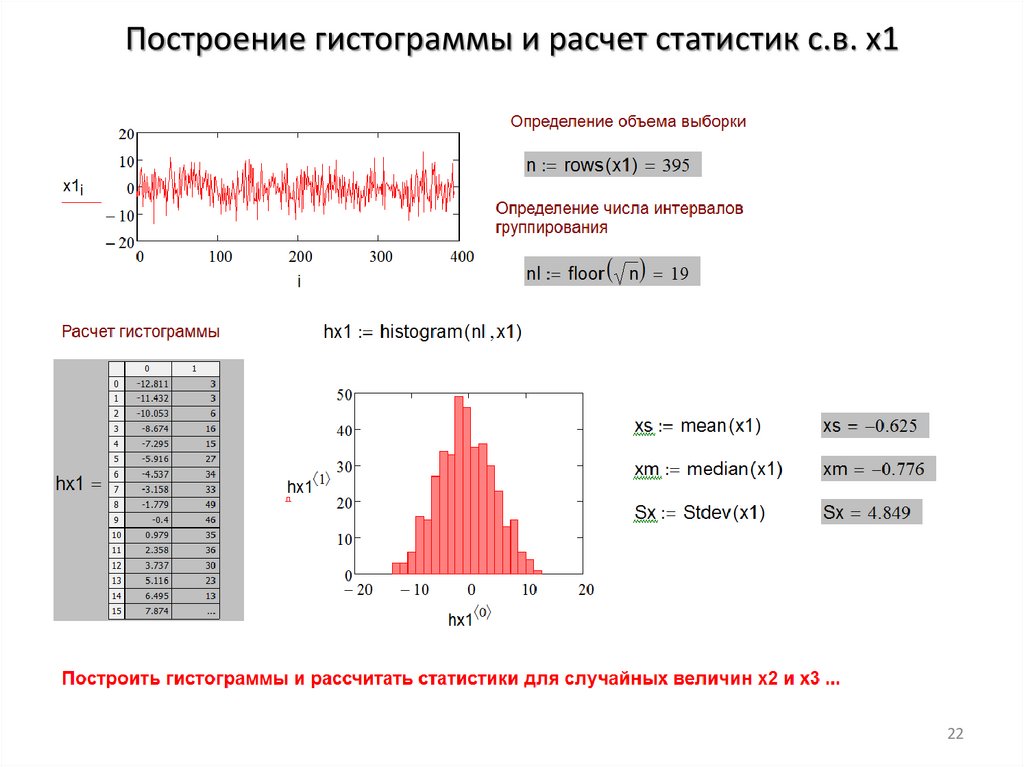
Алгоритм построения гистограммы
статистического распределения
1. Определяем число интервалов группирования ≈n½.
2. Определяем размах случайной величины:
минимальное и максимальное значения.
3. Определяем величину интервалов группирования и их
центры.
4. Подсчитываем число точек, попавших в каждый
интервал группирования.
5. Строим гистограмму: зависимость числа точек,
попавших в каждый интервал группирования, от
центров интервалов.
Алгоритм легко реализуется в программе Mathcad.
21

22.

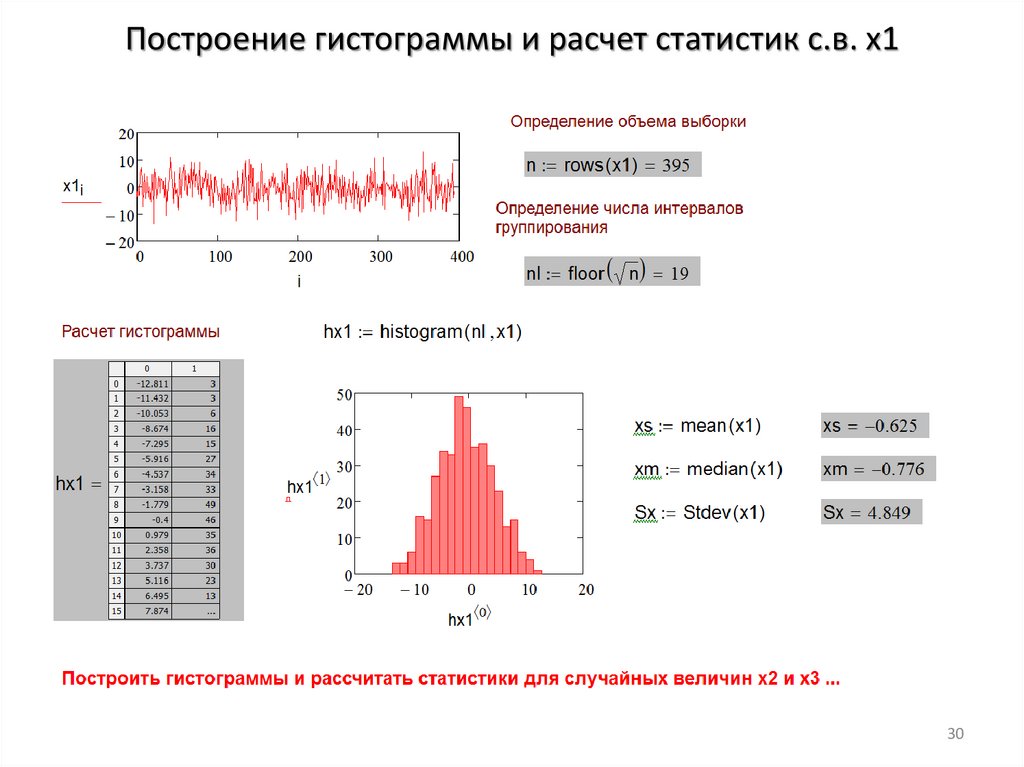
Построение гистограммы и расчет статистик с.в. x1
22

23.

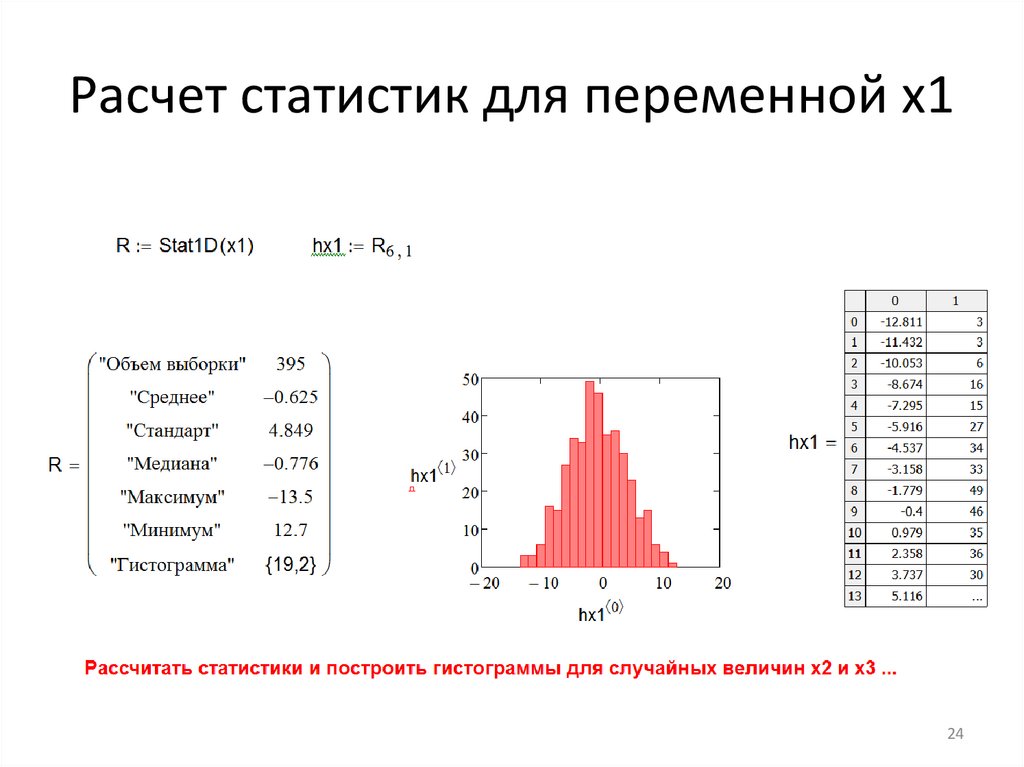
Программирование функции для
вычисления одномерных статистик
23

24.

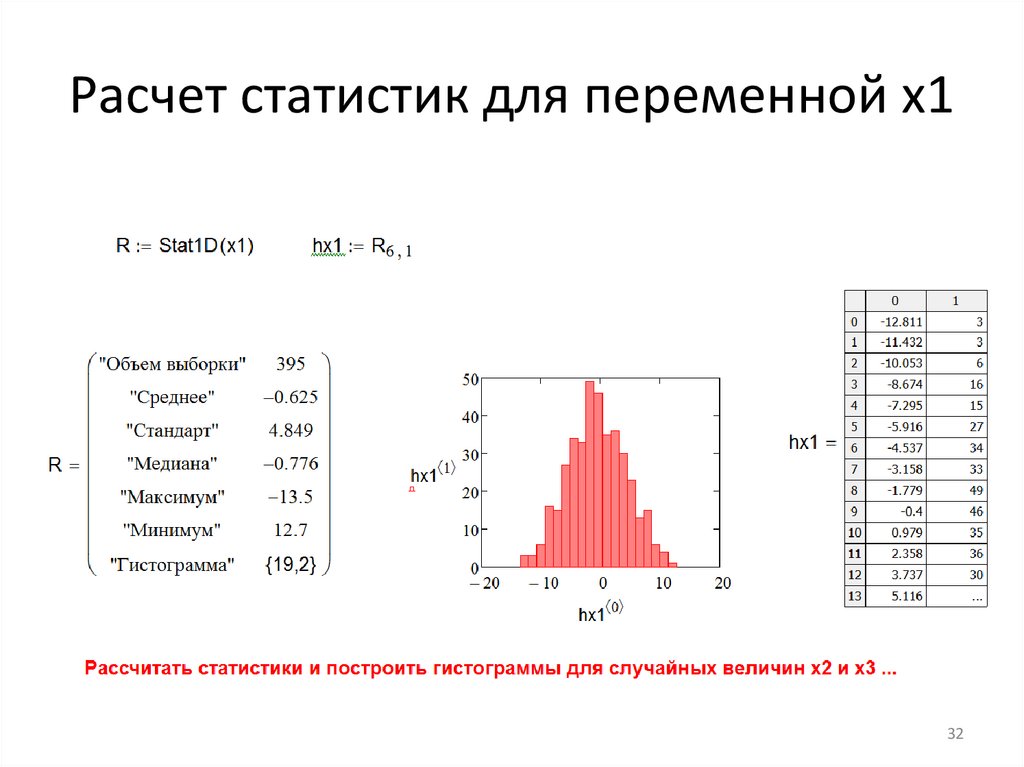
Расчет статистик для переменной x1
24

25.

Практическое задание 1
Решение задач статистической обработки данных в среде
Маткад
Mathcad — программная среда из класса систем автоматизированного проектирования
(Computer Aided Design ), позволяющая решать широкий класс математических и
специализированных инженерных, в т. ч. геофизических задач, с использованием
интуитивного и простого для использования интерфейса.
Работа в Маткад осуществляется в пределах рабочего листа, на котором уравнения и
выражения отображаются наглядным образом в привычной математической транскрипции.
25

26.

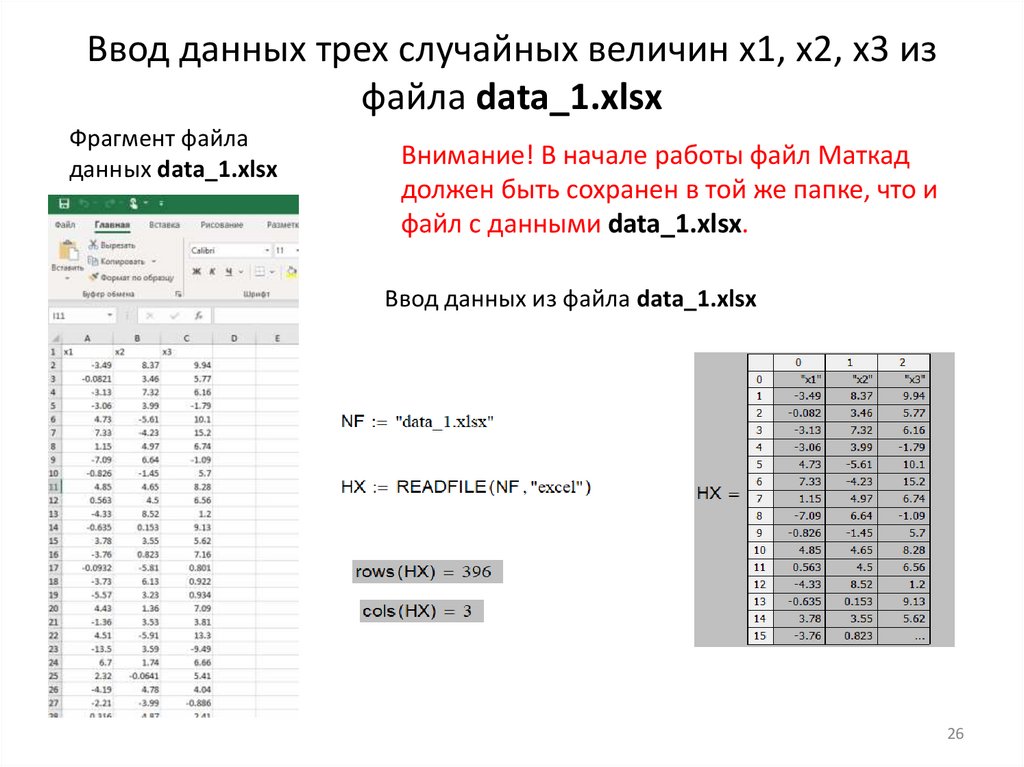
Ввод данных трех случайных величин x1, x2, x3 из
файла data_1.xlsx
Фрагмент файла
данных data_1.xlsx
Внимание! В начале работы файл Маткад
должен быть сохранен в той же папке, что и
файл с данными data_1.xlsx.
Ввод данных из файла data_1.xlsx
26

27.

Выделение текстовых и числовых данных,
определение размеров массива
27

28.

X - система многомерных случайных величин;
x1, x2, x3 – одномерные случайные величины
28

29.

Статистики одномерной случайной величины x1
29

30.

Построение гистограммы и расчет статистик с.в. x1
30

31.

Программирование функции для
вычисления одномерных статистик
31

32.

Расчет статистик для переменной x1
32