Параллельность плоскостей

1.

*
Фесенко Ольга Васильевна
учитель математики ГПОУ «НОВОАЗОВСКИЙ ИНДУСТРИАЛЬНЫЙ
ТЕХНИКУМ»
2021г

2.

* Цели урока
Образовательная:
Знать
виды расположением плоскостей в пространстве;
Признак параллельности плоскостей;
Свойствами параллельных плоскостей
Развивающая:
развивать пространственное воображение студентов,
познавательную и творческую деятельность, память,
внимание;
логическое и алгоритмическое мышление, умения
оперировать с абстрактными
объектами,
математическими понятиями, символами для выражения
количественных и качественных отношений;
Воспитательная: воспитывать ответственное отношение к
учебному труду, волевые качества; формировать
эмоциональную культуру, отношения к математике как к
части общечеловеческой культуры

3.

Д.Грин «Мечты»

4.

Математику нельзя изучать,
наблюдая, как это делает
сосед!
К.Маркс
ДЕЙСТВУЙ:
1. Вспомни определение и признак параллельности плоскостей
2.Приведи 3 примера параллельных плоскостей
3. Выполни практическое задание (слайд 8) в рабочей тетради
4.Выполни чертёж и оформи решение задачи (слайд 9)
5. Запиши два свойства параллельных плоскостей (слайд 10-11),
доказательство каждого из них найди в учебнике (п 11, стр21)
6. Реши задачи (слайды 13-16) самостоятельно, оформляя решения
каждой из них в рабочей тетради (чертеж, дано, решение с
обоснованием, ответ)

5.

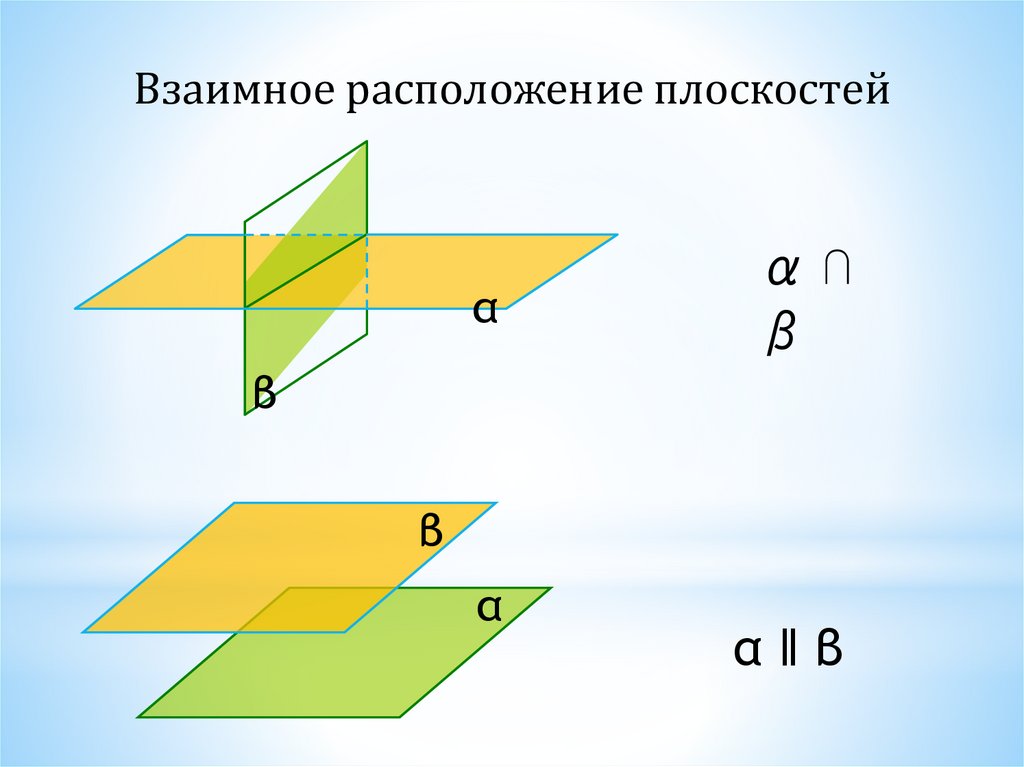
Взаимное расположение плоскостей
α
α⋂
β
β
β
α
α‖β

6.

Плоскости
Пересекаются
Параллельны
α
α
β
β
α∩β
α || β

7.

*
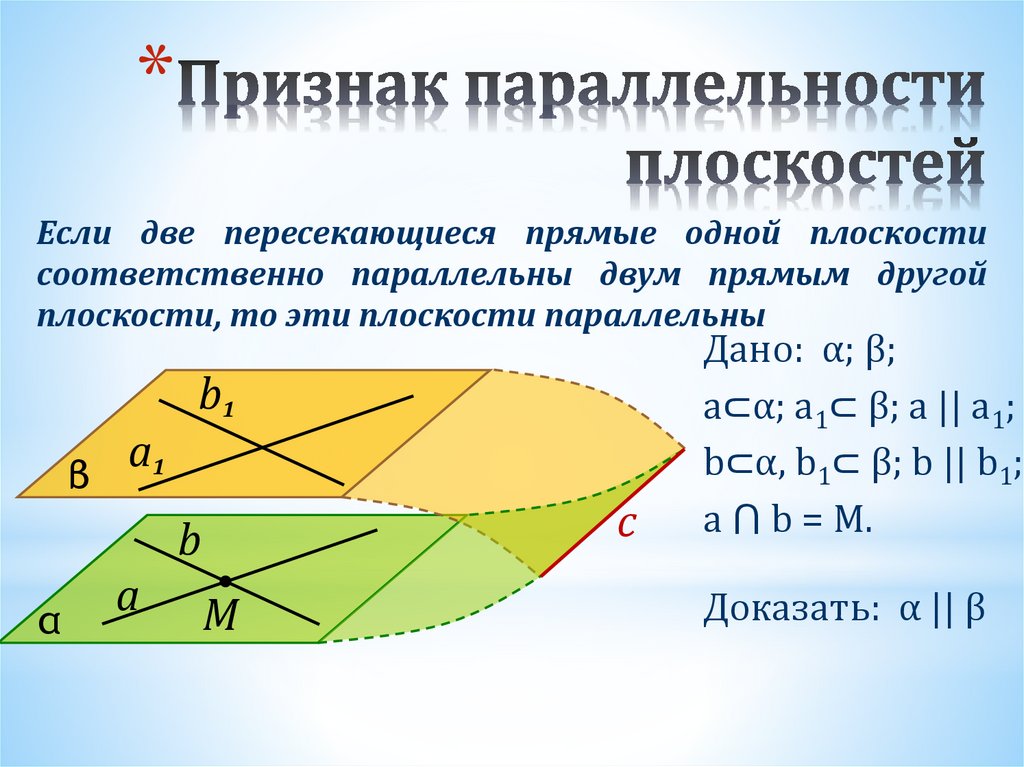
Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны
b1
β
a1
с
b
α
a
М
Дано: α; β;
a⊂α; a1⊂ β; a || a1;
b⊂α, b1⊂ β; b || b1;
a ⋂ b = M.
Доказать: α || β

8.

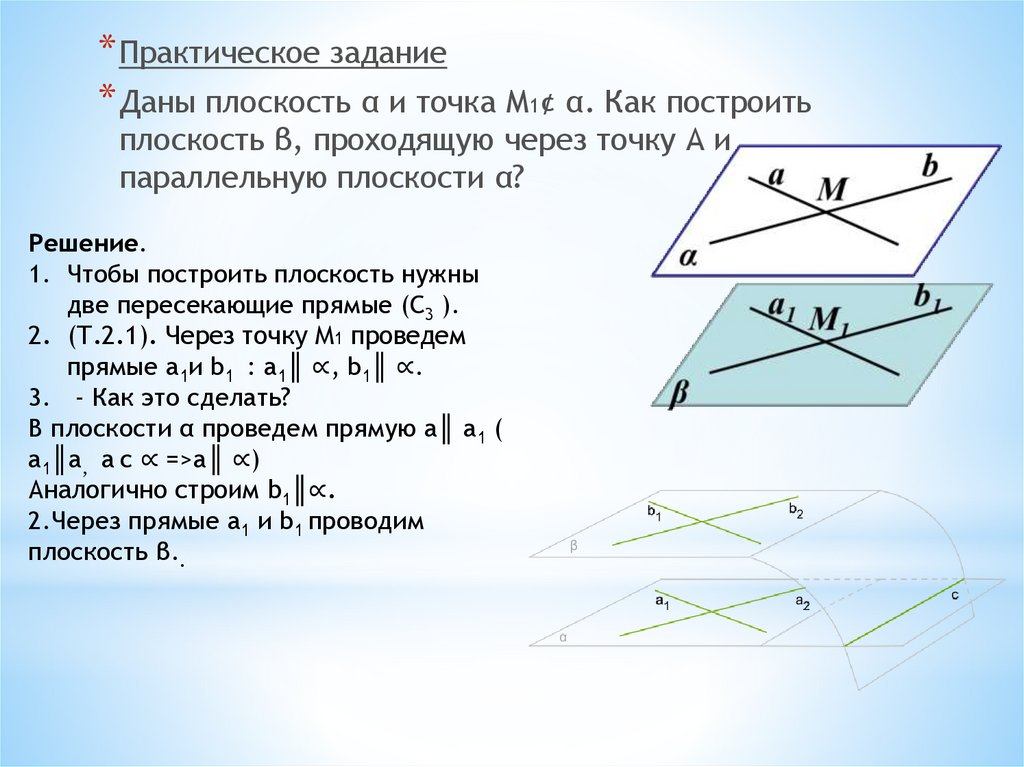
* Практическое задание
* Даны плоскость α и точка М1¢ α. Как построить
плоскость β, проходящую через точку А и
параллельную плоскости α?
Решение.
1. Чтобы построить плоскость нужны
две пересекающие прямые (С3 ).
2. (Т.2.1). Через точку М1 проведем
прямыe a1и b1 : a1║ ∝, b1║ ∝.
3. - Как это сделать?
В плоскости α проведем прямую а║ a1 (
а1║a, а с ∝ =>a║ ∝)
Аналогично строим b1║∝.
2.Через прямые a1 и b1 проводим
плоскость β..

9.

Дано: ΔАDС. М, К, Р середины ВА, ВС, ВD
соответственно.
SADC = 48 см2.
а) Доказать: МРN║ АDС.
б) Найти: SMNP.
В
N
М
C
Р
А
D

10.

*
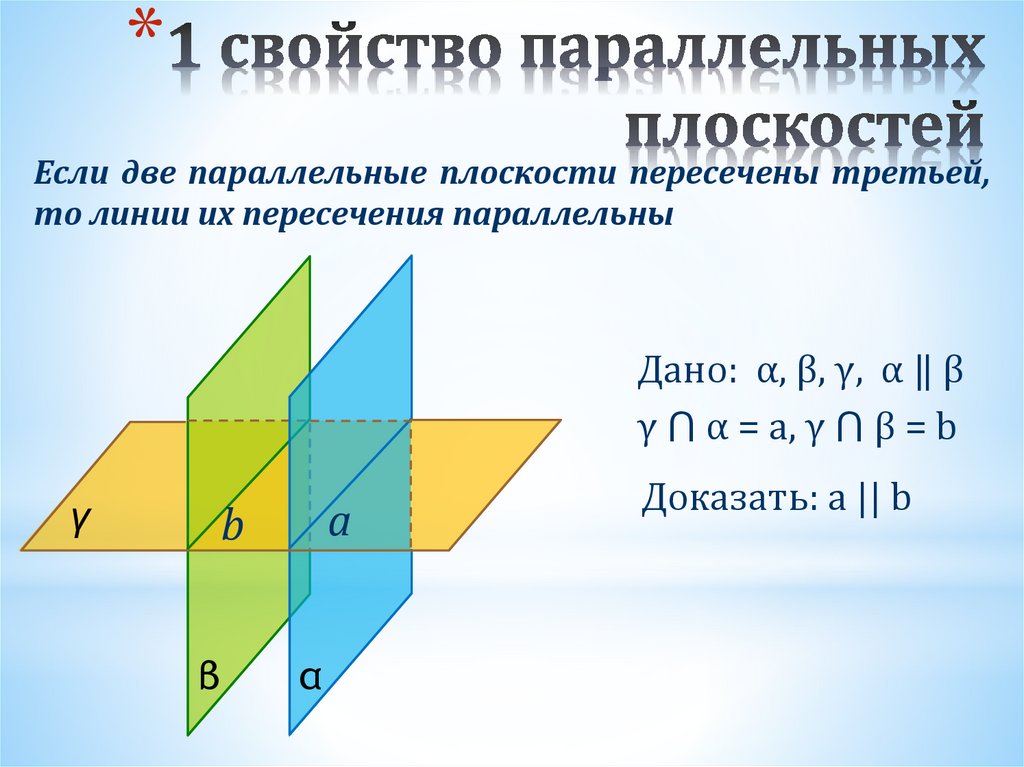
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны
Дано: α, β, γ, α ‖ β
γ ⋂ α = a, γ ⋂ β = b
γ
a
b
β
α
Доказать: a || b

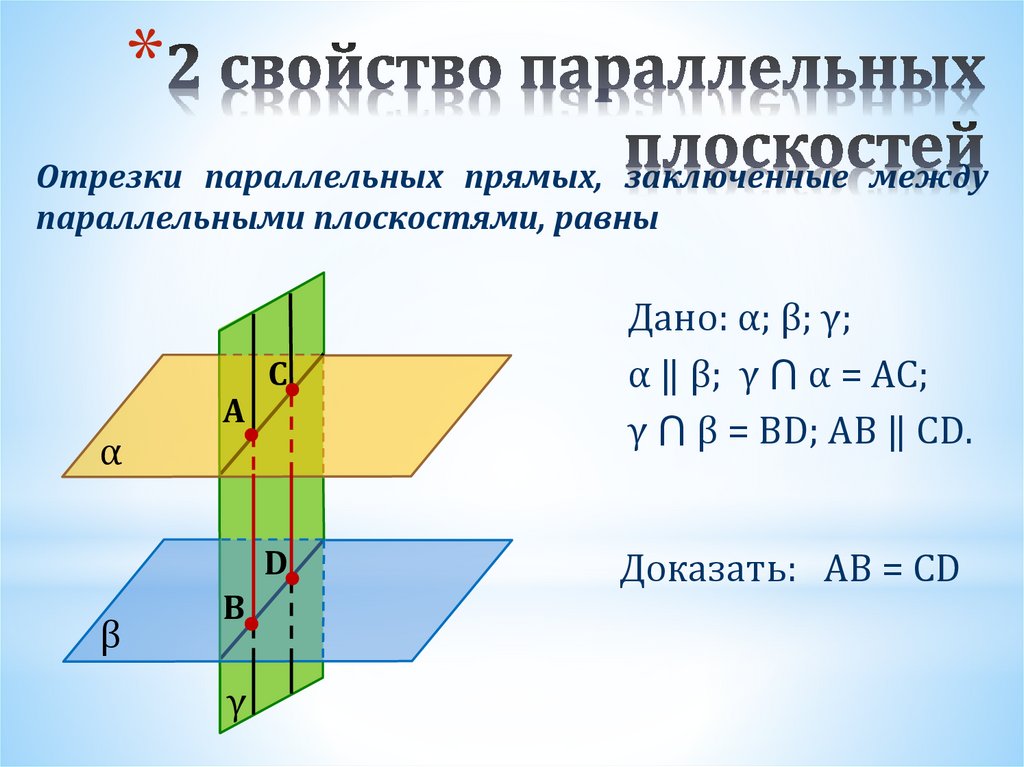
11.

*
Отрезки параллельных прямых, заключенные между
параллельными плоскостями, равны
α
β
A
B
γ
C
Дано: α; β; γ;
α ‖ β; γ ⋂ α = AC;
γ ⋂ β = BD; AB ‖ CD.
D
Доказать: AB = CD

12.

Самостоятельная
работа

13.

* Задача № 1
А
5
Даны параллельные
плоскости и . Через точки
А и В плоскости
проведены параллельные
прямые, пересекающие
плоскость в точках А1 и В1.
Найдите А1В1, если АВ=5см.
В
.
В1
А1

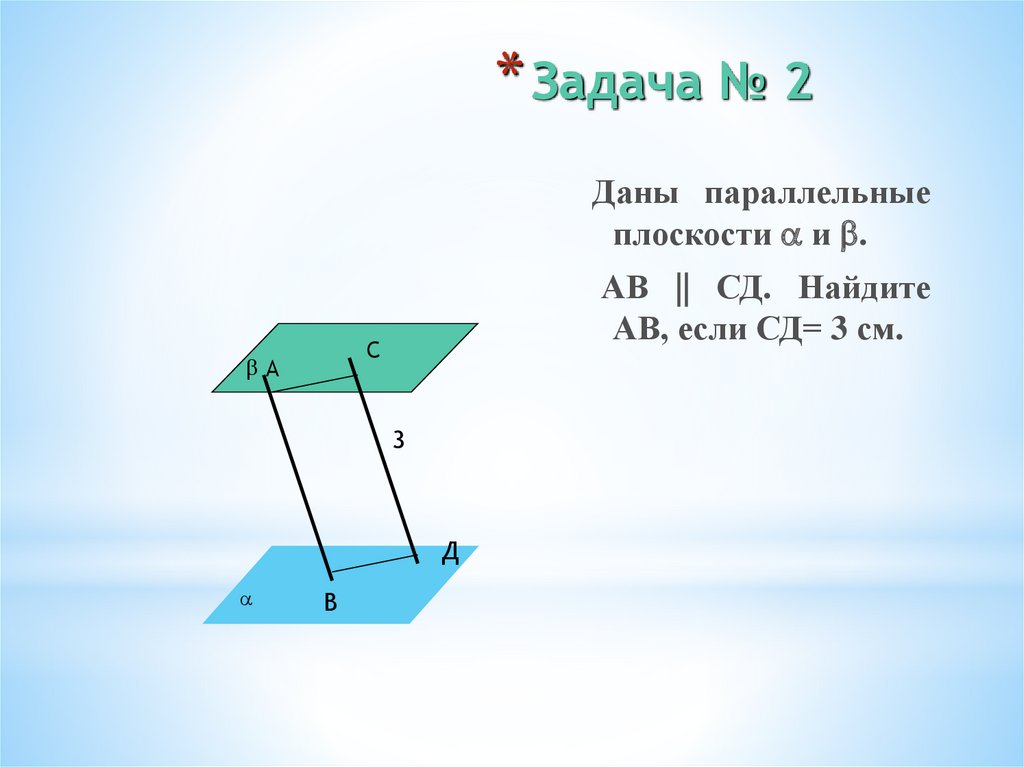
14.

* Задача № 2
Даны параллельные
плоскости и .
АВ || СД. Найдите
АВ, если СД= 3 см.
С
А
3
Д
В

15.

* Задача № 3
Через точку О, расположенную между
параллельными плоскостями и ,
проведены две прямые, которые
пересекают плоскости в точках А и
А1, В и В1
1)
Как расположены прямые АВ и А1В1
?
(Ответ поясните.)
2)
Найдите длину отрезка А1В1,
если АВ = 18 см, АО : ОАг = 3:5.

16.

* Задача № 4
* Через точки В1 и В2 стороны
АВ равностороннего
треугольника ABC проведены
плоскости и ,
параллельные прямой ВС.
1) На какие фигуры делится
этот треугольник
плоскостями и ?
2) Вычислите периметры фигур
АВ1С1 и АВ2С2, если АС = 18 см
и AB1 :АВ = 1:3.