Faraday’s law of induction/

1.

Physics 1
Voronkov Vladimir Vasilyevich

2. Lecture 13

• Faraday’s law of induction
• Lenz’ law
• Eddy currents
• Maxwell’s equations

3.

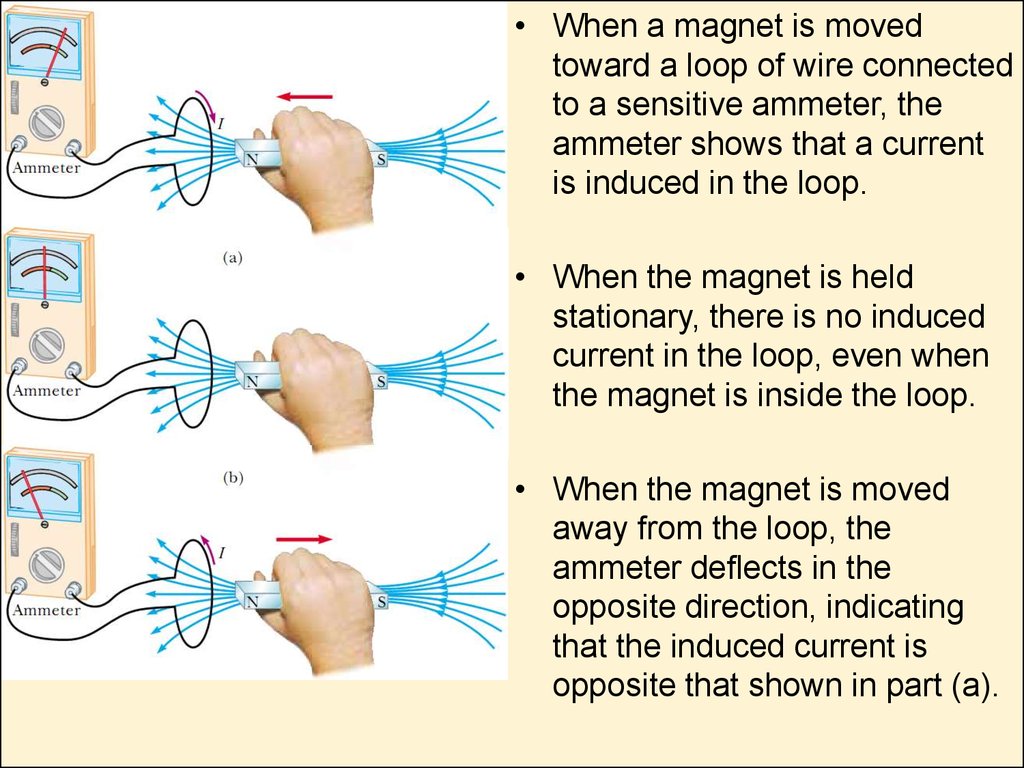
• When a magnet is moved
toward a loop of wire connected
to a sensitive ammeter, the
ammeter shows that a current
is induced in the loop.
• When the magnet is held
stationary, there is no induced
current in the loop, even when
the magnet is inside the loop.
• When the magnet is moved
away from the loop, the
ammeter de ects in the
opposite direction, indicating
that the induced current is
opposite that shown in part (a).

4.

• From these observations, we conclude
that the loop detects that the magnet is
moving relative to it and we relate this
detection to a change in magnetic eld.
• Thus, it shows that a relationship exists
between current and changing magnetic
eld.
• So a current is set up even though no
batteries are present in the circuit! We
call such a current an induced current
and say that it is produced by an induced
emf.

5.

• Initially, when the switch is open, no current is detected by the
ammeter. The same is when the switch is closed ammeter detects no
current.
• When the switch in the primary circuit is either opened or thrown
closed. At the instant the switch is closed, the galvanometer
needle de ects in one direction and then returns to zero. At the
instant the switch is opened, the needle de ects in the opposite
direction and again returns to zero.

6.

• So when the switch was open, and is
closed, the changing current in the
primary circuit creates changing
magnetic field in the iron ring, which
creates current in the secondary coil.
• When the switch was closed, and is
opened, the current in the primary
circuit also is changing – from some
constant value to zero, it creates
changing magnetic field in the iron
ring, which creates current in the
secondary coil.

7. Summary of the two experiments

An electric current can be induced in a
circuit by a changing magnetic eld. The
induced current exists only while the
magnetic eld through the secondary coil
is changing. Once the magnetic eld
reaches a steady value, the current in
the coil disappears.

8. Faraday’s Law of Induction

• The emf induced in a circuit is directly
proportional to the time rate of change of
the magnetic ux through the circuit.
• Here ФB is the magnetic flux through the
circuit:

9. Loop in a uniform magnetic field

A conducting loop that encloses an
area A in the presence of a uniform
magnetic eld B. The angle
between B and the normal to the
loop is Q.
FB=BAcosQ
An emf can be induced in the circuit
in several ways:
The magnitude of B can change with time.
The area enclosed by the loop can change with time.
The angle Q between B and the normal to the loop can change with time.
Any combination of the above can occur.

10. Lenz’s Law

Faraday’s law (e=-dФB/dt) indicates that the
induced emf and the change in ux have opposite
algebraic signs. This has a very real physical
interpretation that has come to be known as Lenz’s
law (2 equivalent variants):
1. The induced current in a loop is in the direction
that creates a magnetic eld that opposes the
change in magnetic ux through the area
enclosed by the loop.
2. Induced currents produce magnetic fields which
tend to cancel the flux changes that induce
them.

11.

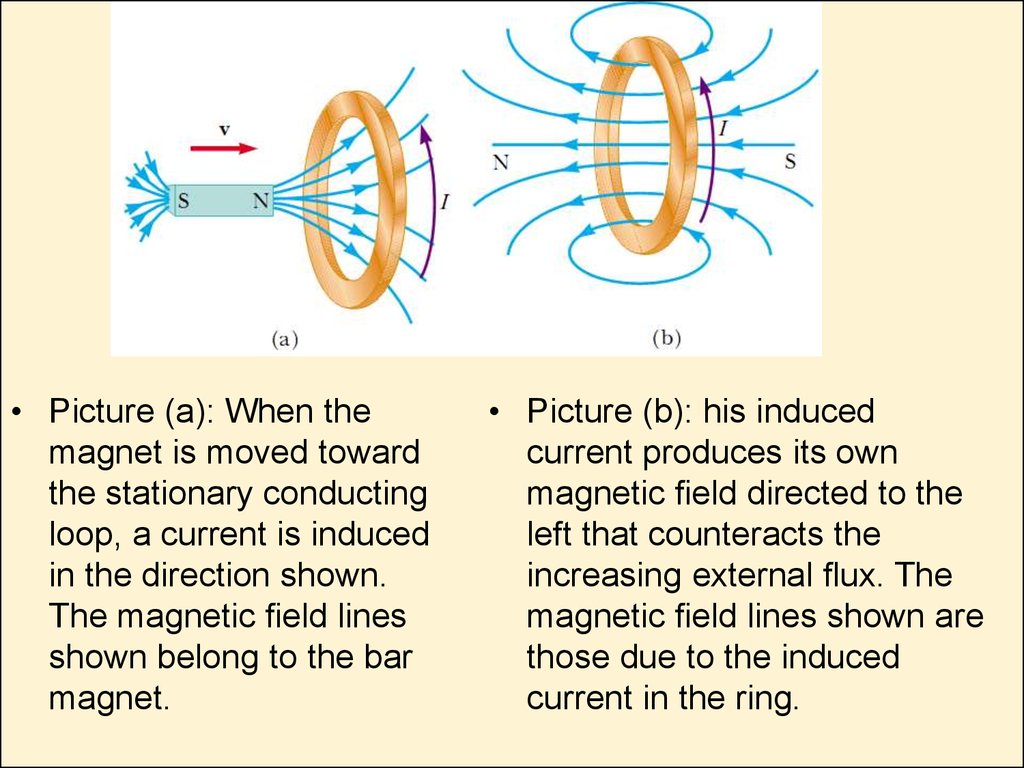
• Picture (a): When the
magnet is moved toward
the stationary conducting
loop, a current is induced
in the direction shown.
The magnetic eld lines
shown belong to the bar
magnet.
• Picture (b): his induced
current produces its own
magnetic eld directed to the
left that counteracts the
increasing external ux. The
magnetic eld lines shown are
those due to the induced
current in the ring.

12.

As the conducting bar slides on the two xed
conducting rails, the magnetic ux due to the
external magnetic eld, through the area enclosed
by the loop, increases in time. By Lenz’s law, the
induced current must be counterclockwise so as
to produce a counteracting magnetic eld directed
out of the page.

13. Induced emf and Electric Fields

A conducting loop of
radius r in a uniform
magnetic eld
perpendicular to the
plane of the loop. If B
changes in time, an
electric eld is induced in
a direction tangent to the
circumference of the
loop.

14.

e=-dФB/dt
The work done by the electric
eld in moving a test charge
q once around the loop is
equal to qe. Because the
electric force acting on the
charge is qE, the work done
by the electric eld in moving
the charge once around the
loop is qE(2pr):

15.

The magnet flux through
the ring is:
Then, using the expressions
on the previous slide, we
can get the electric field:
This result can be
generalized:

16. General form of Faraday’s Law of Induction

• Here
is integration along an enclosed path.
• ФB is a magnetic flux through that enclosed path
(along which the integration
goes).
• The induced electric eld E in this expression is a
nonconservative eld that is generated by a
changing magnetic eld.

17. Eddy Currents

• Circulating currents called eddy currents
are induced in bulk pieces of metal moving
through a magnetic eld.
• Eddy currents are used in many braking systems of
subway and rapid-transit cars.
• Eddy currents are often undesirable because they
represent a transformation of mechanical energy to
internal energy. To reduce this energy loss, conducting
parts are often laminated—that is, they are built up in
thin layers separated by a nonconducting material. This
layered structure increases the resistance of eddy
current paths and effectively con nes the currents to
individual layers.

18.

Eddy currents appears in a solid
conducting plate moving through
a magnetic eld. As the plate
enters or leaves the eld, the
changing magnetic ux induces
an emf, which causes eddy
currents in the plate.

19.

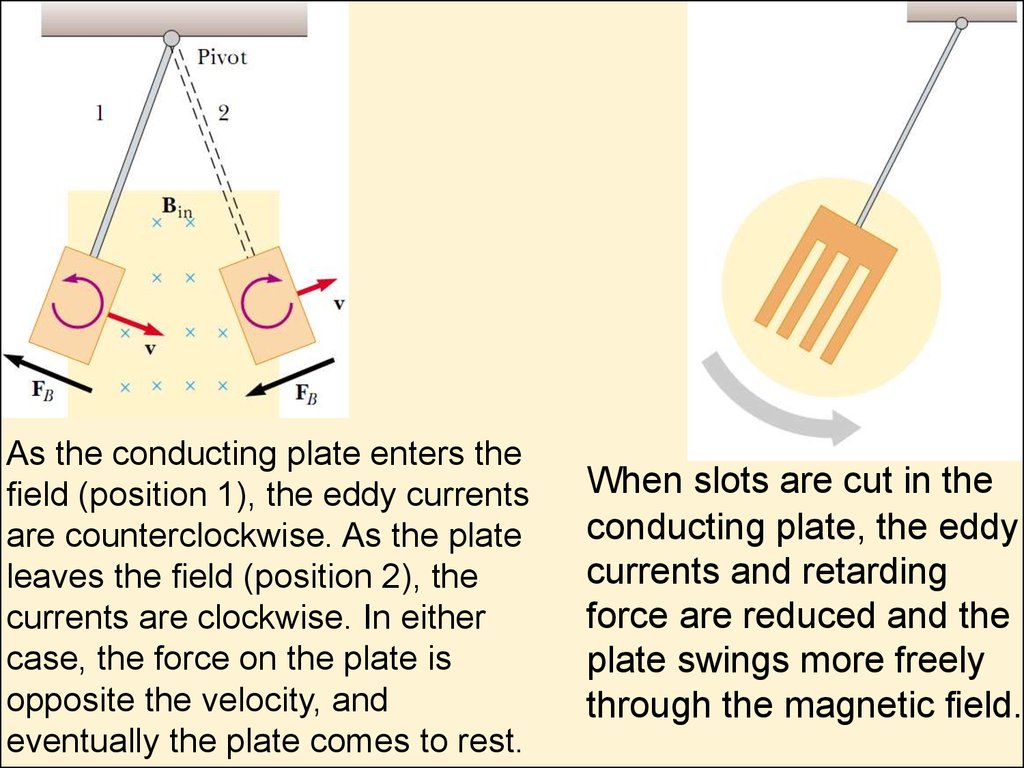
As the conducting plate enters the
eld (position 1), the eddy currents
are counterclockwise. As the plate
leaves the eld (position 2), the
currents are clockwise. In either
case, the force on the plate is
opposite the velocity, and
eventually the plate comes to rest.
When slots are cut in the
conducting plate, the eddy
currents and retarding
force are reduced and the
plate swings more freely
through the magnetic eld.

20. Maxwell’s Equations

Maxwell’s equations applied to free space, that is, in the
absence of any dielectric or magnetic material:
(1)
(2)
(3)
(4)

21.

• Equation (1):
• Here integration goes across an enclosed
surface, q is the charge inside it.
• This is the Gauss’s law: the total electric
ux through any closed surface equals the
net charge inside that surface divided by
e0.
• This law relates an electric eld to the
charge distribution that creates it.

22.

• Equation (2):
• Here integration goes across an enclosed surface.
It can be considered as Gauss’s law in magnetism,
states that the net magnetic ux through a closed
surface is zero.
• That is, the number of magnetic eld lines that enter
a closed volume must equal the number that leave
that volume. This implies that magnetic eld lines
cannot begin or end at any point. It means that there is
no isolated magnetic monopoles exist in nature.

23.

• Equation (3):
• Here integration goes along an enclosed path,
ФB is a magnetic flux through that enclosed path.
• This equation is Faraday’s law of induction,
which describes the creation of an electric
eld by a changing magnetic ux.
• This law states that the emf, which is the line
integral of the electric eld around any
closed path, equals the rate of change of
magnetic ux through any surface area
bounded by that path.

24.

• Equation (4):
• This is Ampère–Maxwell law, or the generalized
form of Ampère’s law. It describes the
creation of a magnetic eld by an electric eld
and electric currents: the line integral of the
magnetic eld around any closed path is the
sum of m0 times the net current through that
path and e0m0 times the rate of change of
electric ux through any surface bounded by
that path.

25. Maxwell’s Equations Symmetry

• Equations (1) and (2) are symmetric, apart
from the absence of the term for magnetic
monopoles in Equation (2).
• Equations (3) and (4) are symmetric in that the
line integrals of E and B around a closed path
are related to the rate of change of magnetic
ux and electric ux, respectively.
• Maxwell’s equations are of fundamental
importance not only to electromagnetism but
to all of science.

26.

• Maxwell’s equations predict the
existence of electromagnetic waves
(traveling patterns of electric and
magnetic elds), which travel with a
speed
the speed of light. Furthermore, the theory
shows that such waves are radiated by
accelerating charges.

27. Units in Si

• Emf
e
• Electric Flux
• Magnetic Flux
• Electric permeability
of free space:
• Magnetic permeability
of free space:
V
ФE
ФB
V*m
T*m2