Основные определения

1.

Механика
– наука о моделировании механического движения.
Движение – всякое изменение материи.
Механическое движение
– перемещение вещественных форм материи в
пространстве и времени.
Материальное тело
– количество материи ограниченное размерами
(занимающее объем в пространстве).
Материальная ПЛОСКОСТЬ, ЛИНИЯ, ТОЧКА – гипотетические
формы, имеющие соответственно ДВА, ОДНО и НОЛЬ измерений в
пространстве.
Абсолютно твердое тело
– тело, расстояние между любыми точками
которого не меняется при любом механическом движении (гипотетическое).
Механическое
взаимодействие
(воздействие)
– воздействие
механических объектов друг на друга, приводящее к изменению механического
движения.

2.

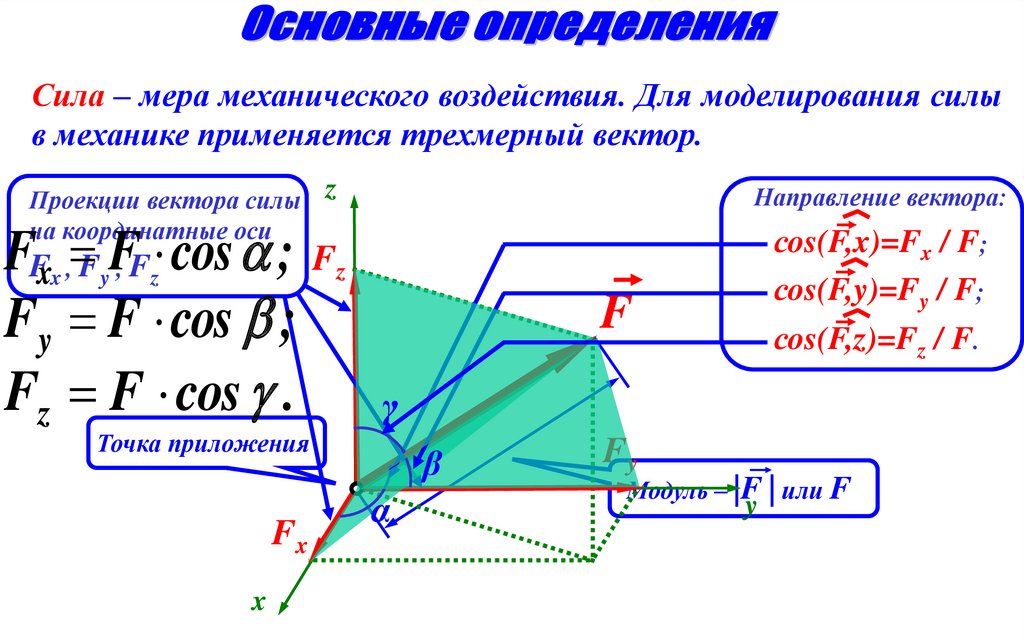
Сила – мера механического воздействия. Для моделирования силы
в механике применяется трехмерный вектор.
Проекции вектора силы z
на координатные оси
Fz
Fxx , Fy , Fz
F F cos ;
Fy F cos ;
Fz F cos .
Направление вектора:
F
γ
Точка приложения
Fx
x
сos(F,x)=Fx / F;
сos(F,y)=Fy / F;
сos(F,z)=Fz / F.
β
α
Fy
Модуль – |F | или F
y

3.

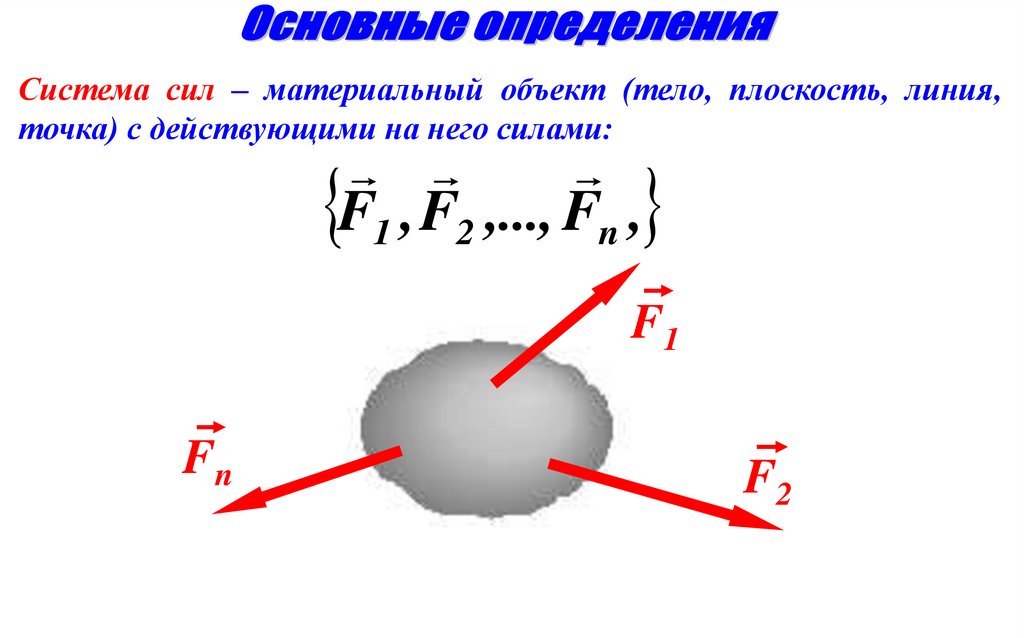
Система сил – материальный объект (тело, плоскость, линия,
точка) с действующими на него силами:
F1 , F2 ,..., Fn ,
F1
Fn
F2

4.

Эквивалентные системы сил – системы, придающие
механическому объекту одинаковое изменение движения:
F1 ,..., Fn Ф1 ,..., Фm
F1
Fn
Фn
F2
Ф1
Ф2

5.

Уравновешенная (эквивалентная нулю) система сил – система сил,
которая будучи добавлена или изъята из механической системы,
не изменяет ее движения:
F1 ,..., Fn 0
Равнодействующая системы сил – одна сила, придающая
механической системе такое-же движение, как и система сил
(сила, заменяющая систему):
F1 ,..., Fn R
Уравновешивающая системы сил – одна сила, которая, будучи
добавлена к системе, делает ее эквивалентной нулю:
*
F1 ,..., Fn , R 0

6.

7.

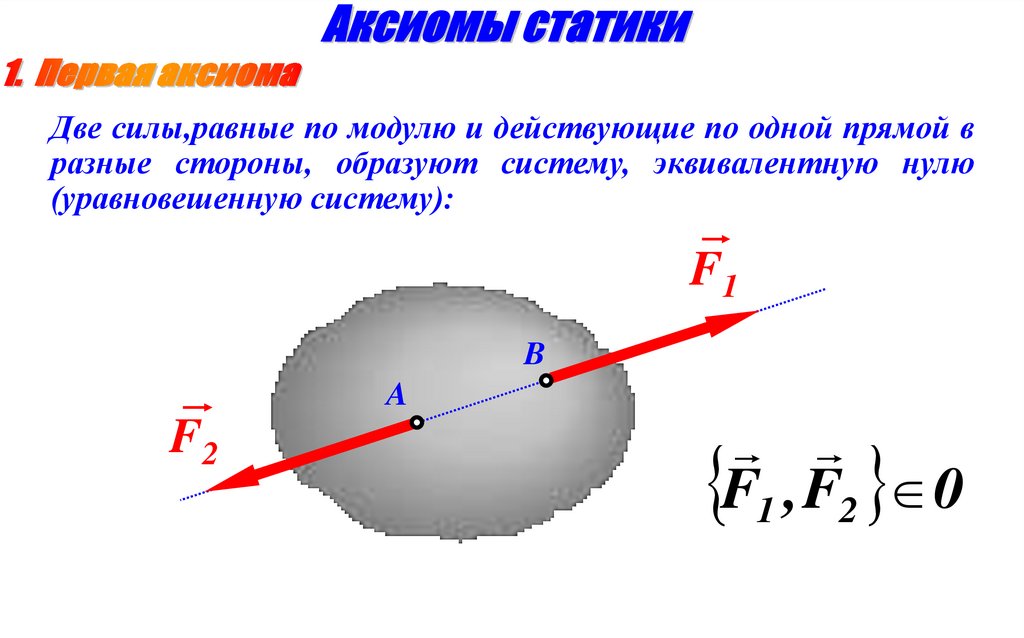
Две силы,равные по модулю и действующие по одной прямой в
разные стороны, образуют систему, эквивалентную нулю
(уравновешенную систему):
F1
B
A
F2
F1 , F2 0

8.

F1 , F2 0
Механическое состояние системы не
нарушится при добавлении или изъятии
системы сил, эквивалентной нулю:
A
F2
B
F1
A
B
F1
F2
Следствие 1
Сила – скользящий вектор, т.е.
может быть перенесена
по
линии действия в любую точку
Доказательство
системы.
Следствие 2
Только такая система имеет
уравновешивающую,
которая
имеет равнодействующую.
Доказательство

9.

Всякое действие вызывает равное ему и противоположное
противодействие.
F2
F1
F1 F2

10.

Система из двух сил, приложенных в одной
R F1 F2
точке всегда имеет равнодействующую.
2
2
R F1 F2 2 F1 F2 cos F1 , F2
F1
F1
A
F1
F1
F2
R
F2
Обратное утверждение:
F2 Силу можно разложить на две
составляющих
бессчетным
F2 числом способов.

11.

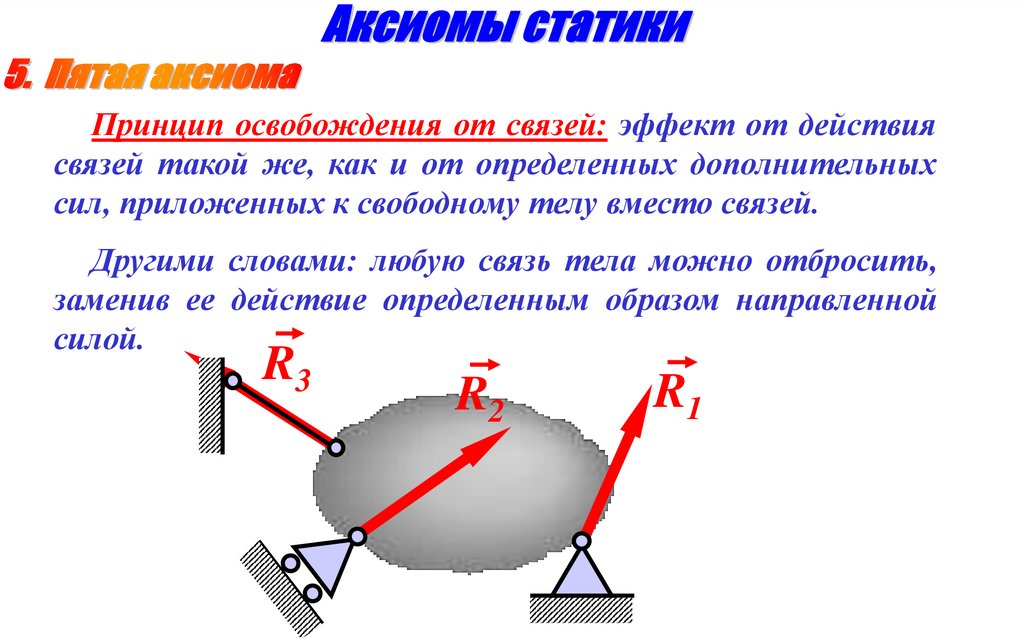
Принцип освобождения от связей: эффект от действия
связей такой же, как и от определенных дополнительных
сил, приложенных к свободному телу вместо связей.
Другими словами: любую связь тела можно отбросить,
заменив ее действие определенным образом направленной
силой.
R3
R1
R2

12.

Аксиома отвердевания: Равновесие системы не
нарушится при наложении дополнительных связей. В
частности, если все точки тела скрепить абсолютно
жестко.
Прием расширения габаритов: Все точки равновесной
системы можно прикрепить абсолютно жестко к
любому окружающему объему, вплоть до бесконечного.
Таким образом, габариты системы могут быть
расширены вплоть до бесконечных.

13.

Рассматривается контакт гладких поверхностей, трением
между телами можно пренебречь.
Связи без трения называются идеальными.
R
R 01
R
90
R
1
0
2 900
90
R
900 2
900
Реакция
гладкой
поверхности направлена
всегда
по общей
нормалито
к
Если
одна
из соприкасающихся
поверхностей
имеет
заострение,
поверхности
тела и по
поверхности
связи вповерхности.
точке их касания.
реакция направлена
нормали к другой

14.

Жесткие
тонкие связи
связи ––абсолютно
жесткие
невесомые
Гибкие тонкие
канаты, нити,
цепи,
тросы стержни
и др. –
различной конфигурации. Трение в идеальных шарнирах
относятся
к
классу
так
называемых
нерастяжимых
нитей.
отсутствует.
R3
R
R21
R1 R
R2
Реакциягибкой
невесомого
и шарнирно
закрепленного
Реакция
тонкой связи
направлена вдоль
самой связистержня
направлена вдоль линии, соединяющей центры шарниров

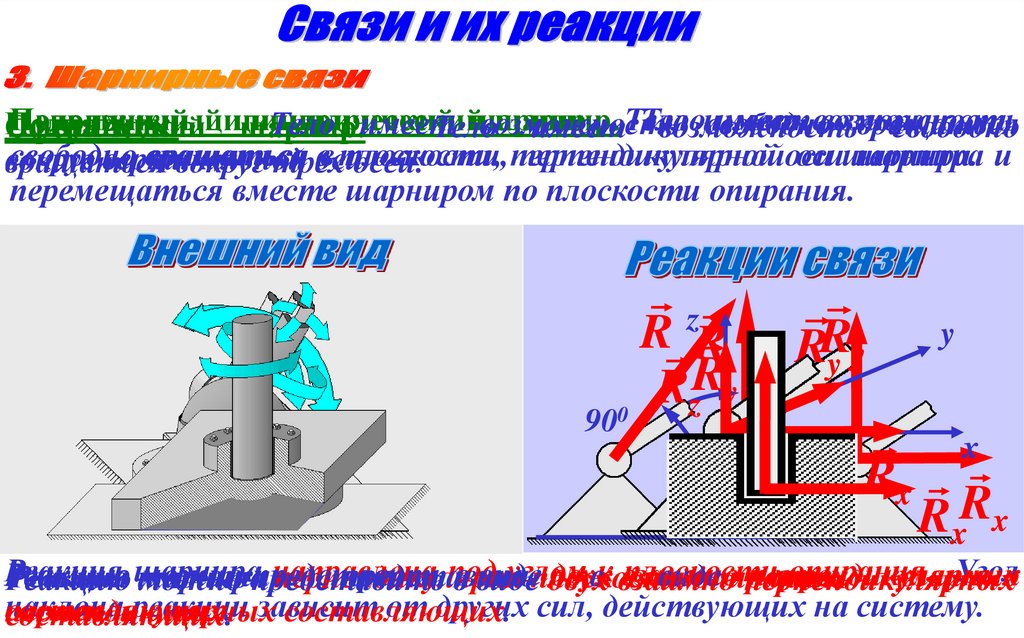
15.

Подвижный цилиндрический
Неподвижный
цилиндрический
шарнир.
шарнир.
Тело
имеет
имеет возможность
возможность
Подпятник.
Тело имеет
возможность
свободно
вращаться
Сферический
шарнир.
Тело
имеетТело
возможность
свободно
свободно
вращаться
вв плоскости,
плоскости,
перпендикулярной
перпендикулярнойоси
осишарнира.
шарнира и
вокруг
вертикальной
оси
вращаться
вокруг трех
осей.
перемещаться вместе шарниром по плоскости опирания.
z
R R
Ry
R
z
0
RR
yy
90
α
Rx
y
x
R
R x
x
Реакция
направлена
под
углом
плоскости
опирания.
Угол
можно
представить
в виде
двух
взаимно
перпендикулярных
Реакцию
можно
представить
вк взаимно
виде
трех
взаимно
Реакция шарнира
шарнира
перпендикулярна
плоскости
опирания.
перпендикулярных
наклона
реакции зависит
от других сил, действующих на систему.
составляющих.
перпендикулярных
составляющих.

16.

Один конец твердого тела (балки) неподвижно защемлен (в стене).
Связь не допускает линейных перемещений тела и поворота по всем
координатным осям.
Ry
Rx
М
состоит
из ТРЕХпространства)
составляющихсостоит
(для плоскости)
–
Реакция (для
трехмерного
из ШЕСТИ
проекции реакции
на горизонталь,
реакции на(Rx,
вертикаль
составляющих
– проекции
реакциипроекции
на оси координат
Ry, Rz) ии
момента сил
реакции (момент
или реактивный
момент)
проекции
реактивного
моментазаделки
на оси координат
(Mx, My,
Mz).

17.

F ;
' ''
F F F ;
'
''
F F ;
' ''
F
F ,F 0
' ''
F F , F , F ;
''
''
F F
F ,F 0;
' ''
'
F F , F , F F
F
B
F
A

18.

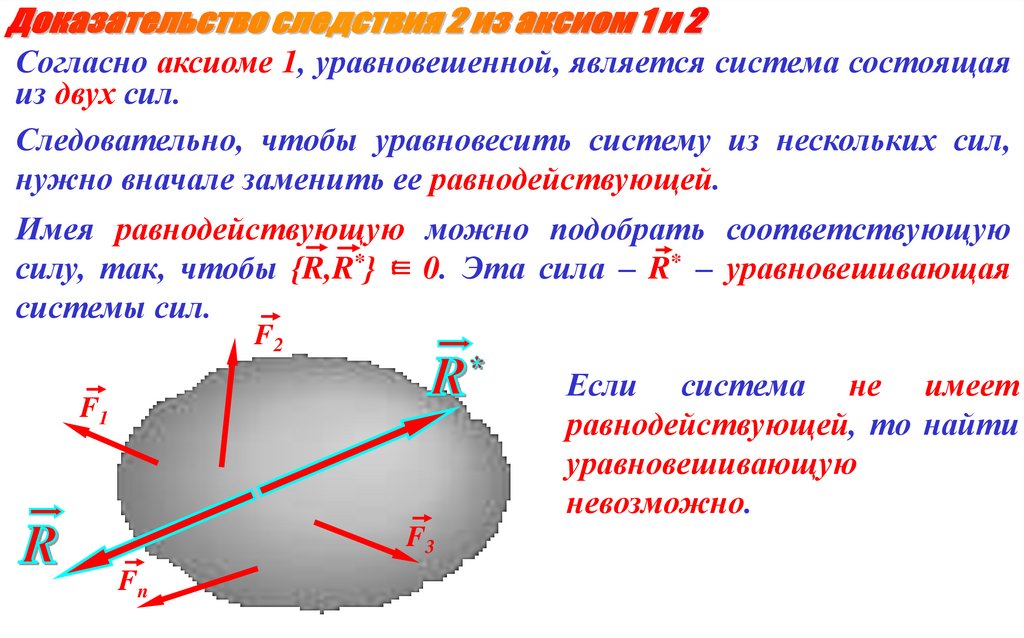
Согласно аксиоме 1, уравновешенной, является система состоящая
из двух сил.
Следовательно, чтобы уравновесить систему из нескольких сил,
нужно вначале заменить ее равнодействующей.
Имея равнодействующую можно подобрать соответствующую
силу, так, чтобы {R,R*} ≡ 0. Эта сила – R* – уравновешивающая
системы сил.
F2
Если система не имеет
равнодействующей, то найти
уравновешивающую
невозможно.
F1
F3
Fn