Понятие многогранника. Правильные многогранники

1.

Понятие
многогранника.
Правильные
многогранники.

2.

Цели урока:
Ввести понятие многогранника
Дать понятие правильных многогранников ( на основе
определения многогранников).
Рассмотреть свойства правильных многогранников.
Познакомить с историческими фактами, связанными с
теорией правильных многогранников.
Развивать познавательный интерес учащихся, учить их
видеть связь между математикой и окружающей жизнью;

3.

Теория
Теориямногогранников,
многогранников,ввчастности
частности
выпуклых
выпуклыхмногогранников,
многогранников,
—
—одна
однаиз
изсамых
самыхувлекательных
увлекательныхглав
глав
геометрии.
геометрии.
Л.
Л.А.
А.Люстерник
Люстерник

4.

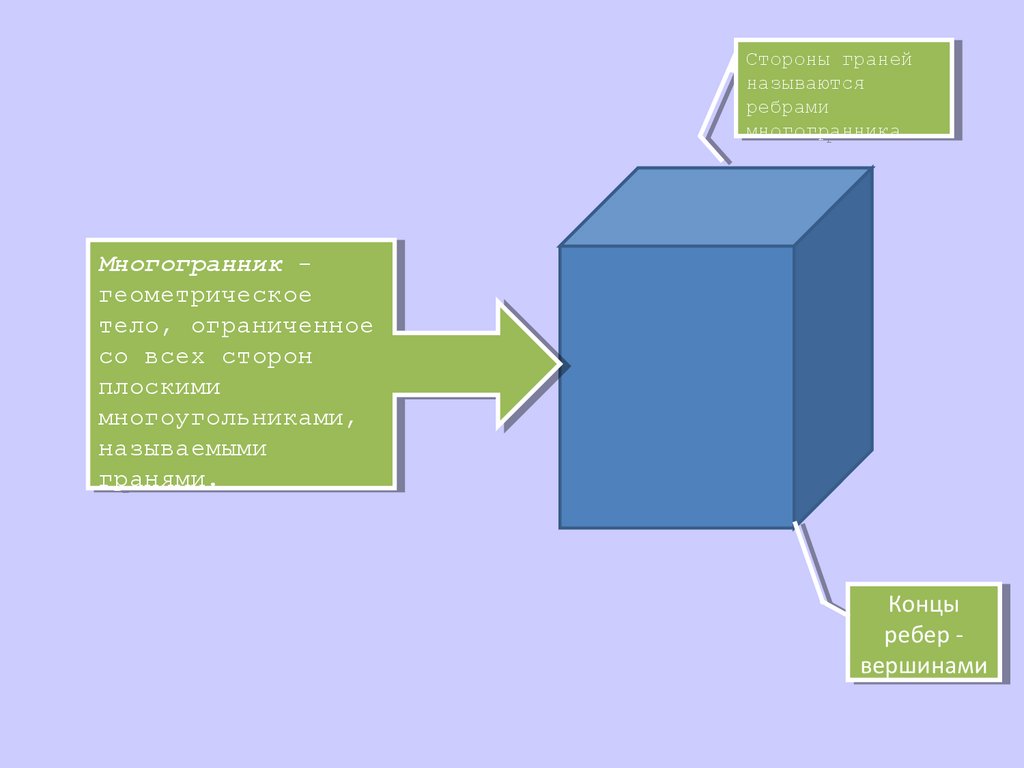
Стороны
Стороны граней
граней
называются
называются
ребрами
ребрами
многогранника
многогранника
Многогранник
Многогранник -геометрическое
геометрическое
тело,
тело, ограниченное
ограниченное
со
со всех
всех сторон
сторон
плоскими
плоскими
многоугольниками,
многоугольниками,
называемыми
называемыми
гранями.
гранями.
Концы
Концы
ребер
ребер-вершинами
вершинами

5.

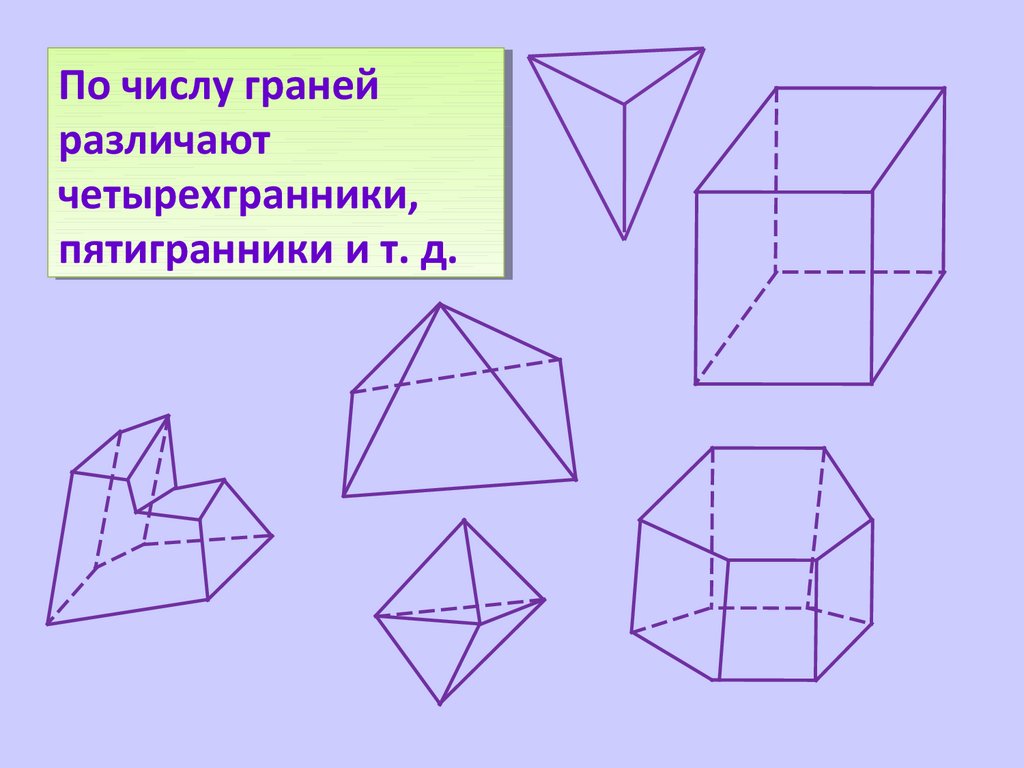
По
По числу
числу граней
граней
различают
различают
четырехгранники,
четырехгранники,
пятигранники
пятигранники ии т.т. д.
д.

6.

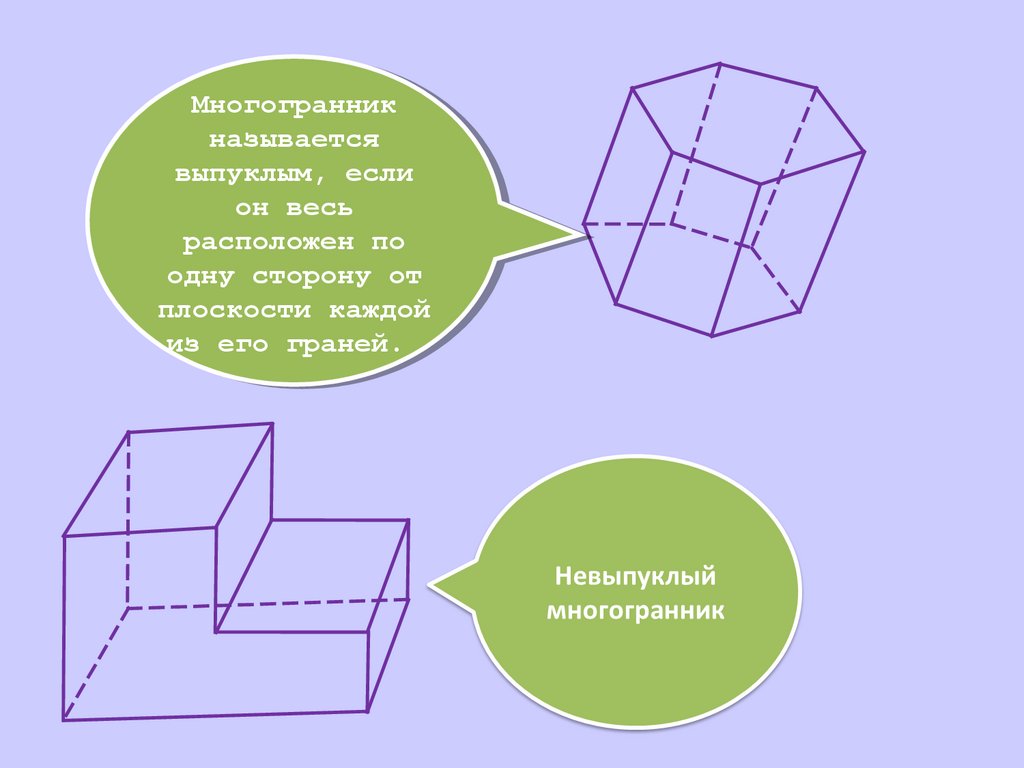
Многогранник
Многогранник
называется
называется
выпуклым,
выпуклым, если
если
он
он весь
весь
расположен
расположен по
по
одну
одну сторону
сторону от
от
плоскости
плоскости каждой
каждой
из
из его
его граней.
граней.

7.

ВВкаждой
каждойвершине
вершинемногогранника
многогранникадолжно
должносходиться
сходиться
столько
столькоправильных
правильныхnn––угольников,
угольников,чтобы
чтобысумма
суммаих
ихуглов
угловбыла
была
00
меньше
меньше360
360 ..
00
βk
βk << 360
360
β-градусная
β-градуснаямера
мераугла
угламногоугольника
многоугольника
kk––число
числомногоугольников,
многоугольников,сходящихся
сходящихсявводной
однойвершине
вершине
многогранника
многогранника
ВВлюбом
любомвыпуклом
выпукломмногограннике
многогранникесумма
суммачисла
числаграней
гранейии
числа
числавершин
вершинбольше
большечисла
числаребер
реберна
на2.
2.
Г+В=Р+2
Г+В=Р+2

8.

Правильным
Правильнымназывается
называетсямногогранник,
многогранник,уукоторого
котороговсе
все
грани
граниявляются
являютсяправильными
правильнымимногоугольниками,
многоугольниками,иивсе
все
многогранные
многогранныеуглы
углыпри
привершинах
вершинахравны.
равны.

9.

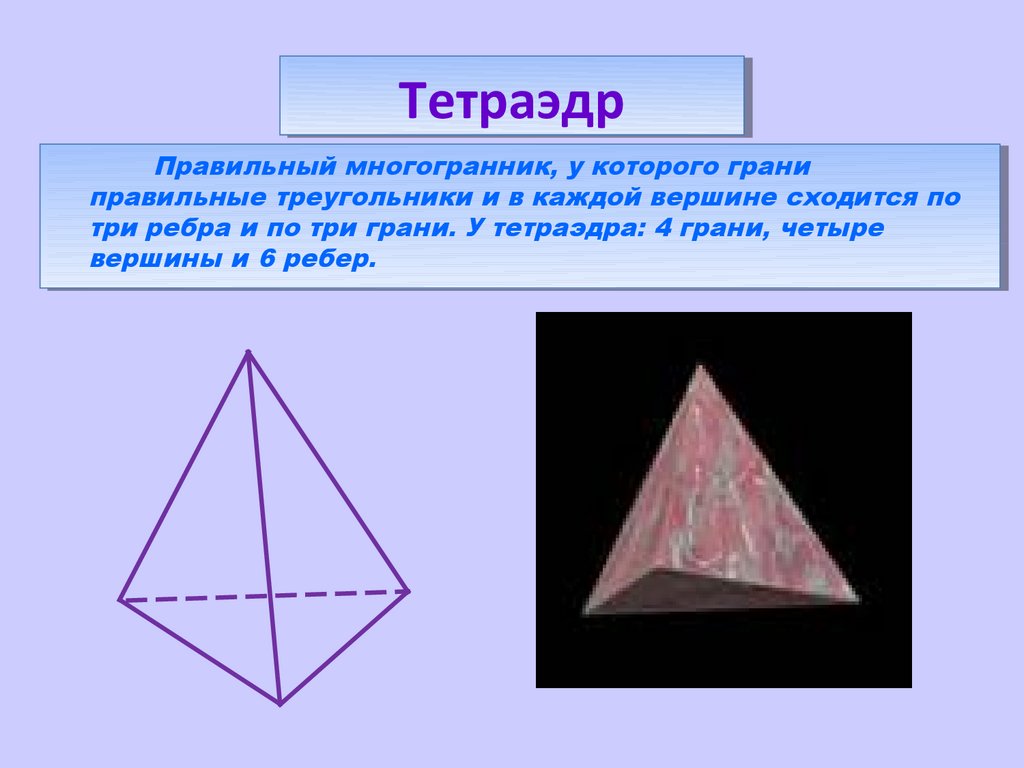
Тетраэдр
Тетраэдр
Правильный
Правильныймногогранник,
многогранник,уукоторого
которогограни
грани
правильные
правильныетреугольники
треугольникиииввкаждой
каждойвершине
вершинесходится
сходитсяпо
по
три
триребра
ребраиипо
потри
триграни.
грани.УУтетраэдра:
тетраэдра:44грани,
грани,четыре
четыре
вершины
вершиныии66ребер.
ребер.

10.

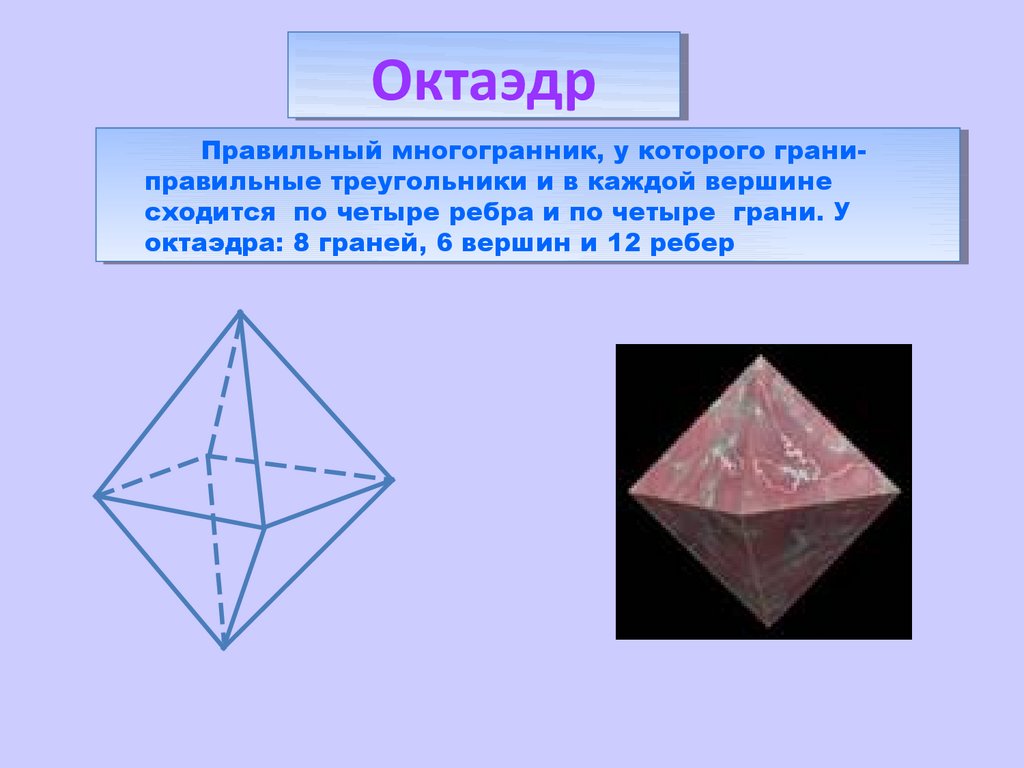
Октаэдр
Октаэдр
Правильный
Правильныймногогранник,
многогранник,уукоторого
которогограниграниправильные
правильныетреугольники
треугольникиииввкаждой
каждойвершине
вершине
сходится
сходится по
почетыре
четыреребра
ребраиипо
почетыре
четыре грани.
грани.УУ
октаэдра:
октаэдра:88граней,
граней,66вершин
вершинии12
12ребер
ребер

11.

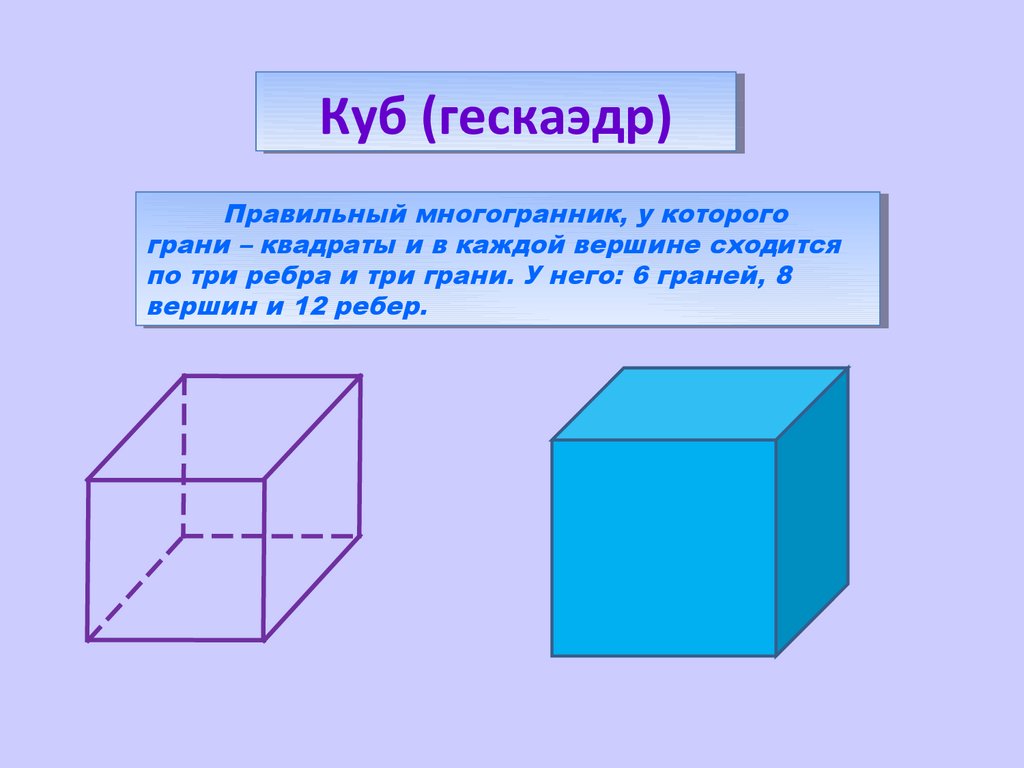
Куб
Куб (гескаэдр)
(гескаэдр)
Правильный
Правильныймногогранник,
многогранник,уукоторого
которого
грани
грани––квадраты
квадратыииввкаждой
каждойвершине
вершинесходится
сходится
по
потри
триребра
ребраиитри
триграни.
грани.УУнего:
него:66граней,
граней,88
вершин
вершинии12
12ребер.
ребер.

12.

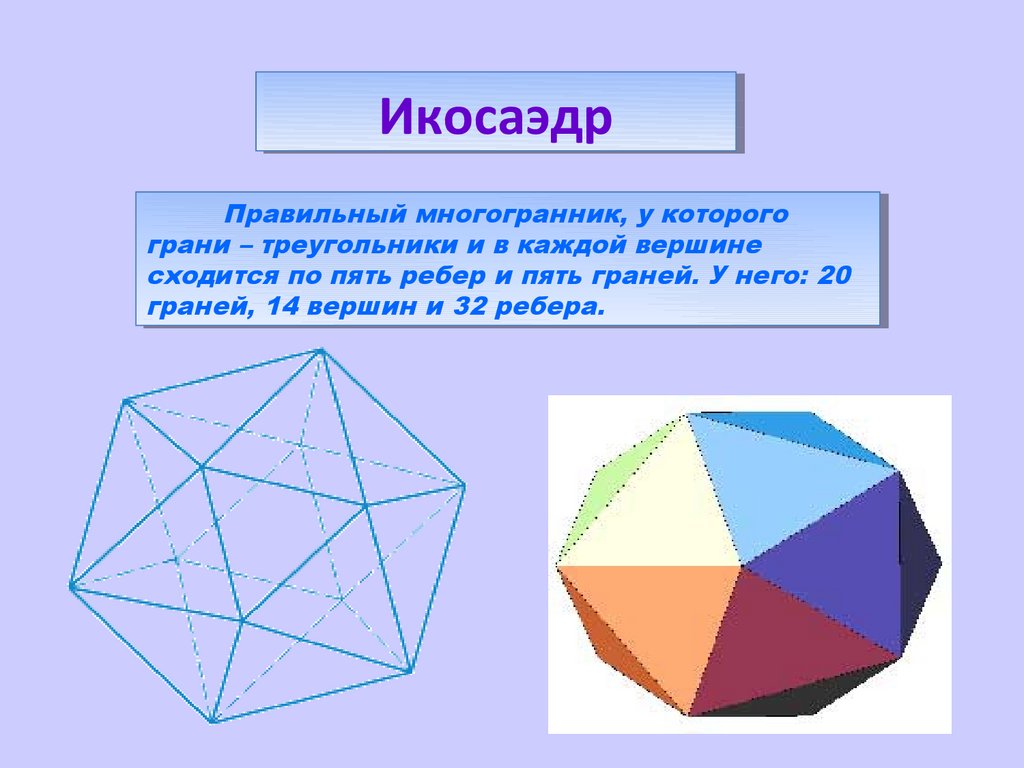
Икосаэдр
Икосаэдр
Правильный
Правильныймногогранник,
многогранник,уукоторого
которого
грани
грани––треугольники
треугольникиииввкаждой
каждойвершине
вершине
сходится
сходитсяпо
попять
пятьребер
ребериипять
пятьграней.
граней.УУнего:
него:20
20
граней,
граней,14
14вершин
вершинии32
32ребера.
ребера.

13.

Додекаэдр
Додекаэдр
Правильный
Правильныймногогранник,
многогранник,уукоторого
которогограни
грани
правильные
правильныепятиугольники
пятиугольникиииввкаждой
каждойвершине
вершине
сходится
сходитсяпо
потри
триребра
ребраиитри
триграни.
грани.УУдодекаэдра:12
додекаэдра:12
граней,
граней,20
20вершин
вершинии30
30ребер.
ребер.

14.

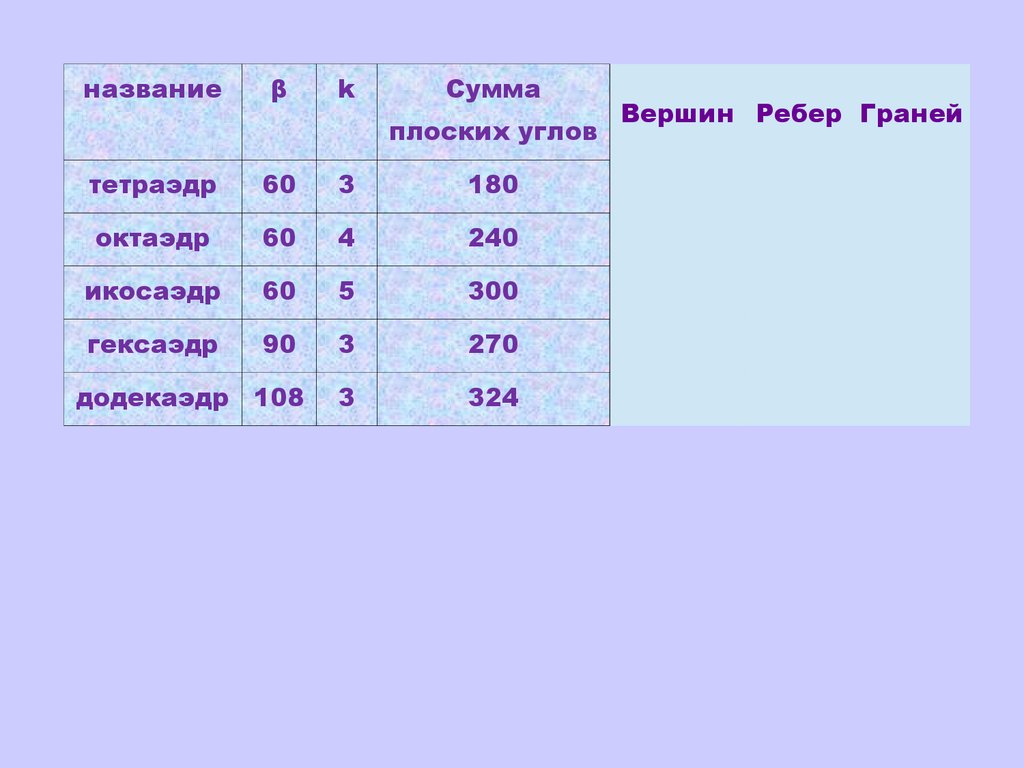
название
β
k
Сумма
плоских углов
тетраэдр
60
3
180
октаэдр
60
4
240
икосаэдр
60
5
300
гексаэдр
90
3
270
3
324
додекаэдр 108
Вершин Ребер Граней

15.

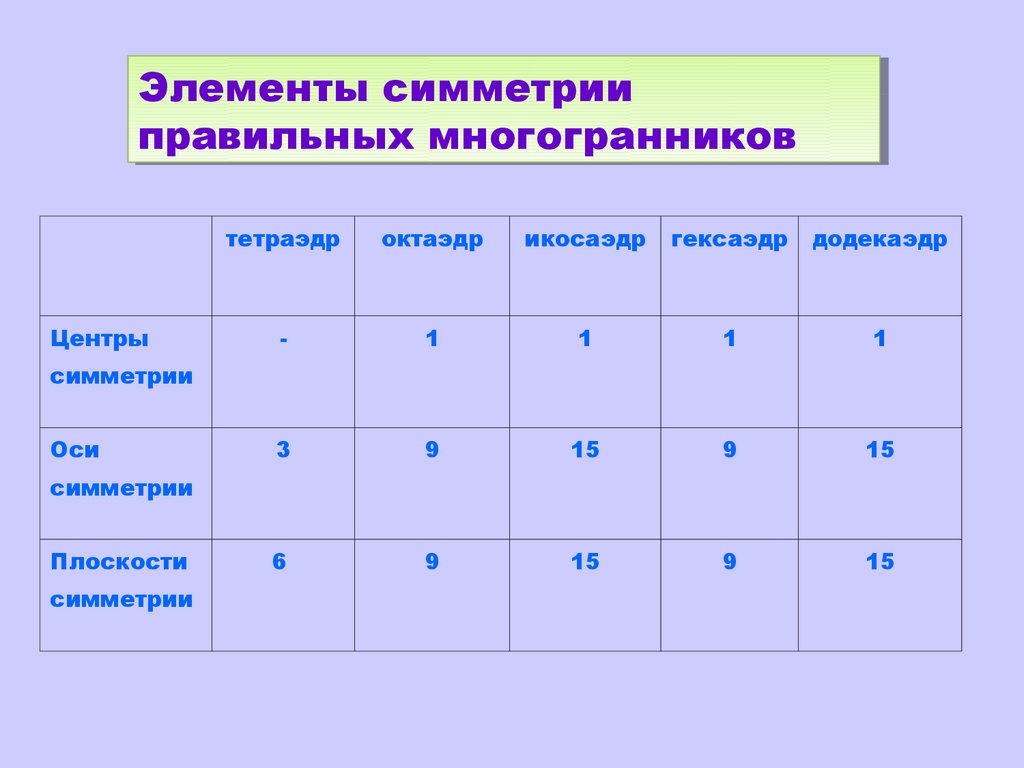
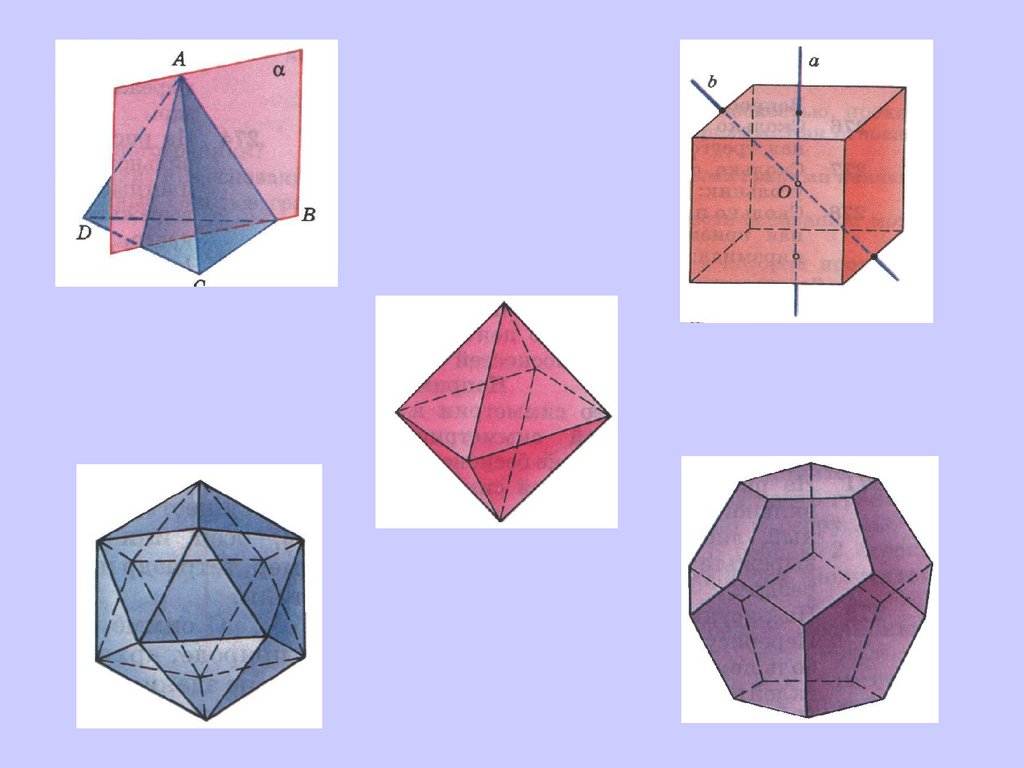
Элементы
Элементы симметрии
симметрии
правильных
правильных многогранников
многогранников
Центры
тетраэдр
октаэдр
икосаэдр
гексаэдр
додекаэдр
-
1
1
1
1
3
9
15
9
15
6
9
15
9
15
симметрии
Оси
симметрии
Плоскости
симметрии

16.

17.

Немного
Немного истории
истории
Все
Все типы
типы правильных
правильных многогранников
многогранников были
были
известны
известны вв Древней
Древней Греции
Греции –– именно
именно им
им
посвящена
посвящена завершающая,
завершающая, XIII
XIII книга
книга «Начал»
«Начал»
Евклида.
Евклида.

18.

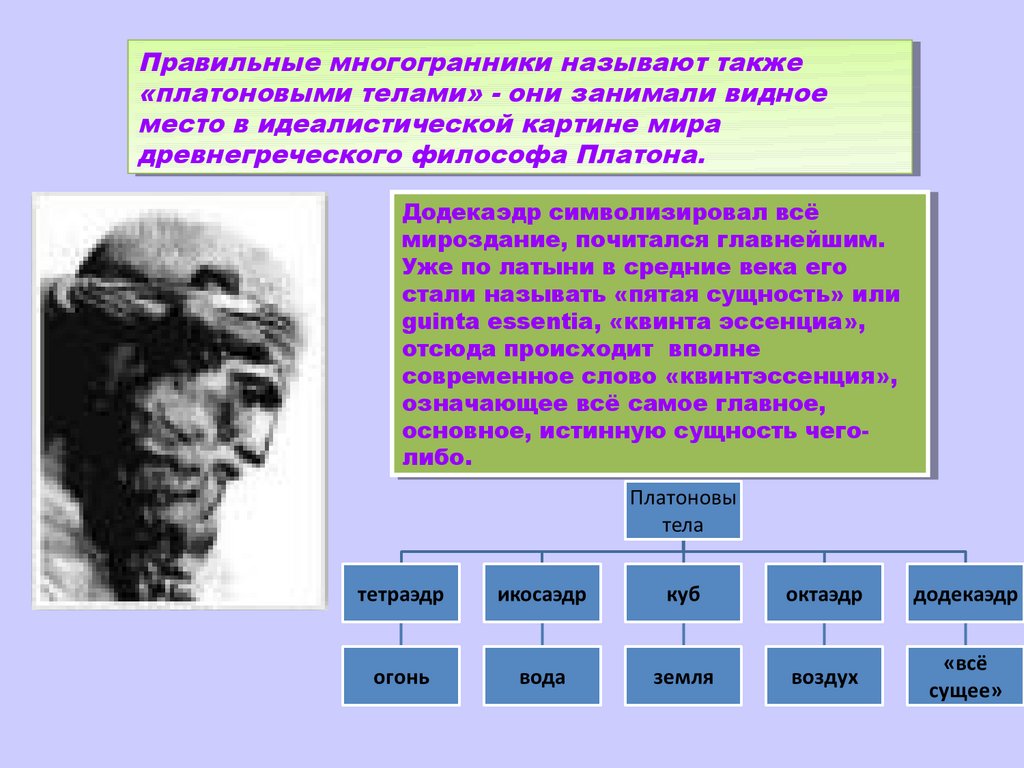
Правильные
Правильныемногогранники
многогранникиназывают
называюттакже
также
«платоновыми
«платоновымителами»
телами»--они
онизанимали
занималивидное
видное
место
местоввидеалистической
идеалистическойкартине
картинемира
мира
древнегреческого
древнегреческогофилософа
философаПлатона.
Платона.
Додекаэдр
Додекаэдрсимволизировал
символизировалвсё
всё
мироздание,
мироздание,почитался
почиталсяглавнейшим.
главнейшим.
Уже
Ужепо
полатыни
латыниввсредние
средниевека
векаего
его
стали
сталиназывать
называть«пятая
«пятаясущность»
сущность»или
или
guinta
guintaessentia,
essentia,«квинта
«квинтаэссенциа»,
эссенциа»,
отсюда
отсюдапроисходит
происходит вполне
вполне
современное
современноеслово
слово«квинтэссенция»,
«квинтэссенция»,
означающее
означающеевсё
всёсамое
самоеглавное,
главное,
основное,
основное,истинную
истиннуюсущность
сущностьчегочеголибо.
либо.

19.

Олицетворение
Олицетворение многогранников
многогранников

20.

Звездчатые
Звездчатые правильные
правильные
многогранники
многогранники

21.

.
Существует
Существует семейство
семейство тел,
тел,
родственных
родственных платоновым
платоновым -- это
это
полуправильные
полуправильные выпуклые
выпуклые
многогранники,
многогранники, или
или Архимедовы
Архимедовы тела.
тела.
УУ них
них все
все многогранные
многогранные углы
углы равны,
равны,
все
все грани
грани -- правильные
правильные
многоугольники,
многоугольники, но
но нескольких
нескольких
различных
различных типов.
типов.

22.

Если
Еслинаблюдать
наблюдатьиирассматривать
рассматривать
многогранные
многогранныеформы,
формы,то
томожно
можноне
не
только
толькопочувствовать
почувствоватьих
ихкрасоту,
красоту,но
ноии
обнаружить
обнаружитьнекоторые
некоторые
закономерности,
закономерности,возможно,
возможно,
имеющие
имеющиеприкладное
прикладноезначение.
значение.
Некоторые
Некоторыеиз
изправильных
правильныхии
полуправильных
полуправильныхтел
телвстречаются
встречаютсявв
природе
природевввиде
видекристаллов,
кристаллов,другие
другие—
—
вввиде
видевирусов,
вирусов,простейших
простейших
микроорганизмов.
микроорганизмов.
Кристаллы
Кристаллы—
—тела,
тела,имеющие
имеющиемногогранную
многогранную
форму.
форму.Вот
Вотодин
одиниз
изпримеров
примеровтаких
такихтел:
тел:кристалл
кристалл
пирита
пирита(сернистый
(сернистыйколчедан
колчеданFeS)
FeS)—
—природная
природная
модель
модельдодекаэдра.
додекаэдра.Пирит
Пирит(от
(отгреч.
греч.“пир”
“пир”—
—огонь)
огонь)—
—
сернистое
сернистоежелезо
железоили
илисерный
серныйколчедан,
колчедан,наиболее
наиболее
распространенный
минерал
из
группы
сульфидов.
распространенный минерал из группы сульфидов.
Размеры
Размерыкристаллов
кристалловпирита
пиритачасто
частодостигают
достигают
нескольких
несколькихсантиметров
сантиметровииявляются
являютсяхорошим
хорошим
коллекционным
коллекционнымматериалом.
материалом.От
Отдругих
другихподобных
подобных
ему
емуминералов
минераловотличается
отличаетсятвердостью:
твердостью:царапает
царапает
стекло.
стекло.

23.

Замечено,
Замечено,что
чтонаша
нашаматушка-Земля
матушка-Земля
последовательно
последовательнопроходит
проходитэволюцию
эволюциюправильных
правильных
объемных
объемныхфигур.
фигур.Существует
Существуетмного
многоданных
данныхоо
сравнении
сравненииструктур
структуриипроцессов
процессовЗемли
Землисс
вышеуказанными
вышеуказаннымифигурами.
фигурами.Полагают,
Полагают,что
чточетырем
четырем
геологическим
геологическимэрам
эрамЗемли
Землисоответствуют
соответствуютчетыре
четыре
силовых
силовыхкаркаса
каркасаправильных
правильныхПлатоновских
Платоновскихтел:
тел:
Протозою
Протозою--тетраэдр
тетраэдр(четыре
(четыреплиты),
плиты),Палеозою
Палеозою-гексаэдр
гексаэдр(шесть
(шестьплит)
плит),Мезозою
,Мезозою--октаэдр
октаэдр(восемь
(восемь
плит)
плит),Кайнозою
,Кайнозою--додекаэдр
додекаэдр(двенадцать
(двенадцатьплит).
плит).
Существует
Существуетгипотеза,
гипотеза,по
покоторой
которойядро
ядроЗемли
Землиимеет
имеетформу
форму
иисвойства
свойстварастущего
растущегокристалла,
кристалла,оказывающего
оказывающего
воздействие
воздействиена
наразвитие
развитиевсех
всехприродных
природныхпроцессов,
процессов,
идущих
идущихна
напланете.
планете.«Лучи»
«Лучи»этого
этогокристалла,
кристалла,ааточнее
точнееего
его
силовое
силовоеполе,
поле,обусловливают
обусловливаютикосаэдроикосаэдрододекаэдрическую
додекаэдрическуюструктуру
структуруЗемли,
Земли,проявляющуюся
проявляющуюсявв
том,
том,что
чтоввземной
земнойкоре
корекак
какбы
быпроступают
проступаютпроекции
проекции
вписанных
вписанныхввземной
земнойшар
шарправильных
правильныхмногогранников:
многогранников:
икосаэдра
икосаэдраиидодекаэдра.
додекаэдра.62
62их
ихвершины
вершиныиисередины
серединыребер,
ребер,
называемые
называемыеузлами,
узлами,оказывается,
оказывается,обладают
обладаютрядом
рядом
специфичecких
специфичecкихсвойств,
свойств,позволяющих
позволяющихобъяснить
объяснитьмногие
многие
непонятные
непонятныеявления.
явления.

24.

Если нанести на глобус очаги наиболее крупных
и примечательных культур и цивилизаций
Древнего мира, можно заметить закономерность
в их расположении относительно
географических полюсов и экватора планеты.
Многие залежи полезных ископаемых тянутся
вдоль икосаэдрово-додекаэдровой сетки. Еще
более удивительные вещи происходят в местах
пересечения этих ребер: тут располагаются
очаги древнейших культур и цивилизаций: Перу,
Северная Монголия, Гаити, Обская культура и
другие. В этих точках наблюдаются максимумы и
минимумы атмосферного давления, гигантские
завихрения Мирового океана, здесь
шотландское озеро Лох-Несс, Бермудский
треугольник. Дальнейшие исследования Земли,
возможно, определят отношение к этой красивой
научной гипотезе, в которой, как видно,
правильные многогранники занимают важное
место.

25.

26.

Додекаэдрическая
Додекаэдрическаяструктура,
структура,по
помнению
мнению
Д.
Д.Винтера
Винтера(американского
(американскогоматематика),
математика),
присуща
присущане
нетолько
толькоэнергетическому
энергетическомукаркасу
каркасу
Земли,
Земли,но
ноиистроению
строениюживого
живоговещества.
вещества.
ВВпроцессе
процесседеления
деленияяйцеклетки
яйцеклетки
сначала
сначалаобразуется
образуетсятетраэдр
тетраэдриз
из
четырех
четырехклеток,
клеток,затем
затемоктаэдр,
октаэдр,куб
куби,
и,
наконец,
наконец,додекаэдро-икосаэдрическая
додекаэдро-икосаэдрическая
структура
структурагаструлы.
гаструлы.ИИнаконец,
наконец,самое,
самое,
пожалуй,
пожалуй,главное
главное––структура
структураДНК
ДНК
генетического
генетическогокода
кодажизни
жизни––
представляет
представляетсобой
собойчетырехмерную
четырехмерную
развертку
развертку(по
(пооси
осивремени)
времени)
вращающегося
вращающегосядодекаэдра!
додекаэдра!Таким
Таким
образом,
образом,оказывается,
оказывается,что
чтовся
вся
Вселенная
Вселенная––от
отМетагалактики
Метагалактикииидо
до
живой
живойклетки
клетки––построена
построенапо
поодному
одному
принципу
принципу––бесконечно
бесконечновписываемых
вписываемых
друг
другввдруга
другадодекаэдра
додекаэдраииикосаэдра,
икосаэдра,
находящихся
находящихсямежду
междусобой
собойвв
пропорции
пропорциизолотого
золотогосечения!
сечения!

27.

Впрочем,
Впрочем,многогранники
многогранники--отнюдь
отнюдьне
нетолько
толькообъект
объектнаучных
научных
исследований.
исследований.Их
Ихформы
формы--завершенные
завершенныеиипричудливые,
причудливые,
широко
широкоиспользуются
используютсяввдекоративном
декоративномискусстве.
искусстве.
Надгробный памятник в
кафедральном соборе Солсбери
Титульный лист книги Ж. Кузена
«Книга о перспективе»

28.

Ярчайшим
Ярчайшимпримером
примеромхудожественного
художественногоизображения
изображения
многогранников
многогранниковввXX
XXвеке
векеявляются,
являются,конечно,
конечно,графические
графические
фантазии
фантазииМаурица
МаурицаКорнилиса
КорнилисаЭшера
Эшера(1898-1972),
(1898-1972),
голландского
голландскогохудожника,
художника,родившегося
родившегосяввЛеувардене.
Леувардене.
Мауриц
МаурицЭшер
Эшерввсвоих
своих
рисунках
рисункахкак
какбы
быоткрыл
открылии
интуитивно
интуитивно
проиллюстрировал
проиллюстрировалзаконы
законы
сочетания
сочетанияэлементов
элементов
симметрии,
симметрии,т.е.
т.е.те
тезаконы,
законы,
которые
которыевластвуют
властвуютнад
над
кристаллами,
кристаллами,определяя
определяяии
их
ихвнешнюю
внешнююформу,
форму,ииих
их
атомную
атомнуюструктуру,
структуру,ииих
их
физические
физическиесвойства.
свойства.
Математик,
Математик,так
также
жекак
какиихудожник
художникили
или
поэт,
поэт,создает
создаетузоры,
узоры,ииесли
если
его
егоузоры
узорыболее
болееустойчивы,
устойчивы,то
толишь
лишьпотому,
потому,
что
чтоони
онисоставлены
составленыиз
изидей.
идей.

29.

Тест
Тест«Выбери
«Выбериправильный
правильныйправильный
правильныймногогранник»
многогранник»
1.1. Многогранник,
Многогранник,составленный
составленныйиз
изчетырех
четырехправильных
правильныхмногоугольников:
многоугольников:
А)
В)
Е)Е)Додекаэдр
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр D)
D)Икосаэдр
Икосаэдр
Додекаэдр
2.2. Многогранник,
Многогранник,составленный
составленныйиз
изпятиугольников:
пятиугольников:
А)
В)
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр D)
D)Икосаэдр
Икосаэдр
Е)Е)Додекаэдр
Додекаэдр
3.3. Многогранник,
Многогранник,составленный
составленныйиз
извосьми
восьмитреугольников:
треугольников:
А)
В)
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр D)
D)Икосаэдр
Икосаэдр Е)Е)Додекаэдр
Додекаэдр
4.4. Многогранник,
Многогранник,каждая
каждаявершина
вершинакоторого
которогоявляется
являетсявершиной
вершинойпяти
пятитреугольников:
треугольников:
А)
В)
Е)Е)Додекаэдр
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр D)
D)Икосаэдр
Икосаэдр
Додекаэдр
5.5. Многогранник,
Многогранник,каждая
каждаявершина
вершинакоторого
которогоявляется
являетсявершиной
вершинойтрех
трехквадратов:
квадратов:
А)
В)
Е)Е)Додекаэдр
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр D)
D)Икосаэдр
Икосаэдр
Додекаэдр
6.6. Многогранник
Многогранникссвосьмью
восьмьюгранями:
гранями:
А)
В)
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр
D)
D)Икосаэдр
Икосаэдр
Е)Е)Додекаэдр
Додекаэдр
7.7. Многогранник,
Многогранник,ссчетырьмя
четырьмягранями:
гранями:
А)
В)
А)Тетраэдр
Тетраэдр
В)Куб
Куб С)С)Октаэдр
Октаэдр
D)
D)Икосаэдр
Икосаэдр
Е)Е)Додекаэд
Додекаэд

30.

8.
Многогранник, с шестью вершинами:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
9.
Многогранник, у которого 30 ребер:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
10. Многогранник, у которого 8 вершин:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
11. Многогранник, не имеющий центра симметрии:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
12. Многогранник, имеющий 9 осей и плоскостей симметрии:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
13. Многогранник, имеющий 15 осей и плоскостей симметрии:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
14. Многогранник, у которого 3 оси симметрии:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр
15. Многогранник, имеющий 6 плоскостей симметрии:
А) Тетраэдр
В) Куб
С) Октаэдр
D) Икосаэдр
Е) Додекаэдр

31.

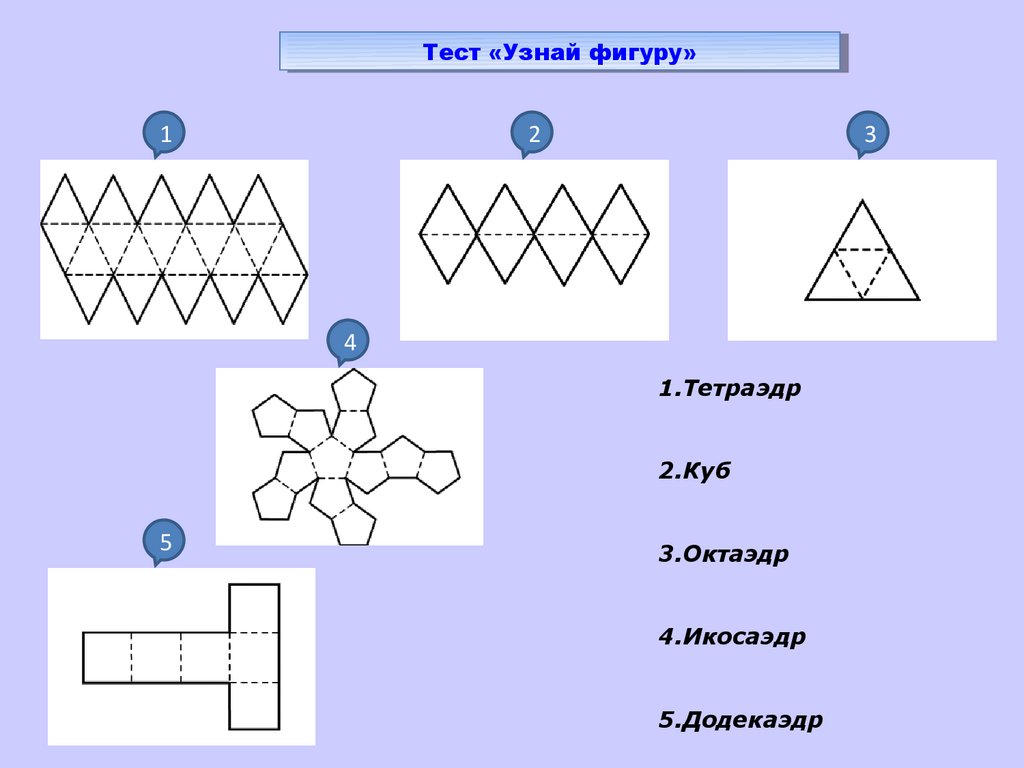
Тест
Тест«Узнай
«Узнайфигуру»
фигуру»
1
2
3
4
1.Тетраэдр
2.Куб
5
3.Октаэдр
4.Икосаэдр
5.Додекаэдр