Компьютерная графика. Лекция 3. Платоновы тела. Аффиные преобразования в пространстве

1.

КОМПЬЮТЕРНАЯ
ГРАФИКА
Лекция 3
«Платоновы тела.
Аффиные преобразования
в пространстве»
Лектор, зав. кафедрой, к.т.н.
Степанченко Илья Викторович
Камышин 2009
Кафедра
автоматизированных
систем обработки
информации и
управления

2.

2.4. ПЛАТОНОВЫ ТЕЛА
Платоновы тела – это правильные выпуклые
многогранники. Правильными многогранниками
(платоновыми
телами)
называются
такие
выпуклые многогранники, все грани которых
являются правильными многоугольниками и все
многогранные углы при вершинах равны между
собой.
Существует
только
пять
правильных
многогранников (это доказал Евклид): тетраэдр,
гексаэдр (куб), октаэдр, икосаэдр и додекаэдр.

3.

2.4. ПЛАТОНОВЫ ТЕЛА
Название
многогранника
Число
граней, Г
Число
ребер, Р
Число
вершин, В
Тетраэдр
(tetrahedron)
4
6
4
Гексаэдр
(hexahedron)
6
12
8
Октаэдр
(octahedron)
8
12
6
Икосаэдр
(icosahedron)
20
30
12
Додекаэдр
(dodecahedron)
12
30
20

4.

2.4. ПЛАТОНОВЫ ТЕЛА
Равенство Эйлера
Г+В=Р+2.
y
y
6
x
8
3
1
z
Гексаэдр
z
Тетраэдр
x

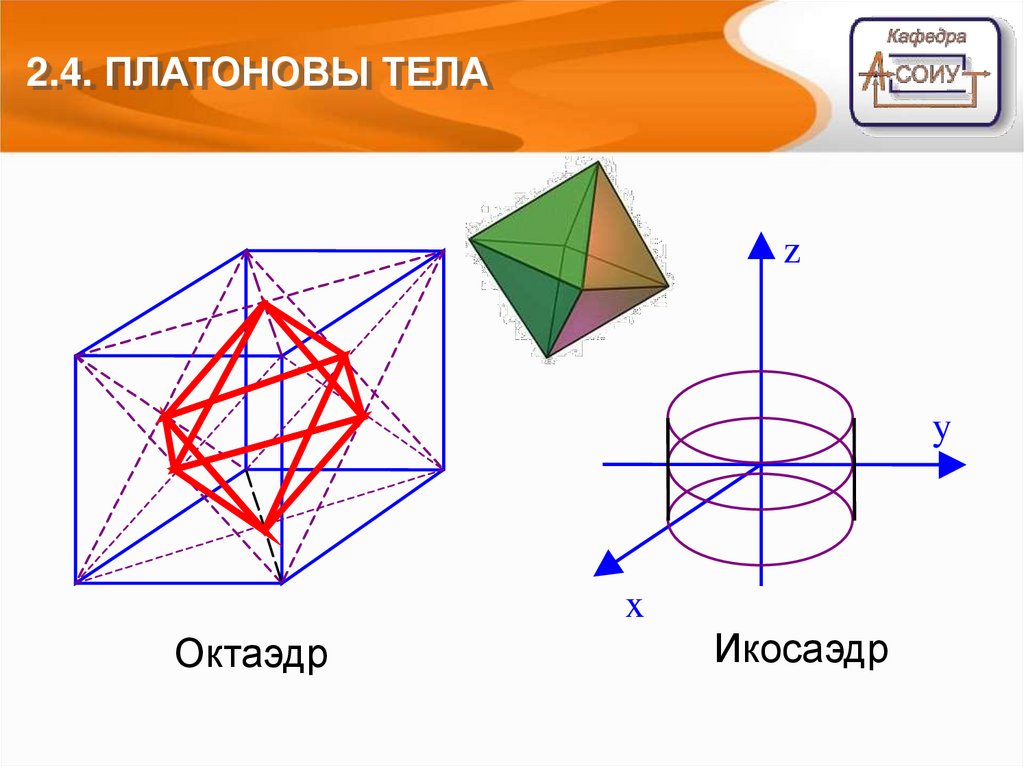
5.

2.4. ПЛАТОНОВЫ ТЕЛА
z
y
x
Октаэдр
Икосаэдр

6.

2.4. ПЛАТОНОВЫ ТЕЛА
6
7
8
6
5
8
9
4
4
10
2
7
5
3
1
10
2
9
1
Икосаэдр
3

7.

2.4. ПЛАТОНОВЫ ТЕЛА
12
8
4
6
2
10
5
7
9
1
3
11
Икосаэдр
Додекаэдр

8.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
1. Поворот относительно прямой (вокруг оси OX,
правосторонняя система).
y r cos( ) r cos cos r sin sin y cos z sin ,
z r sin( ) r sin cos r cos sin z cos y sin ;
z
M’
r
M
y
O
x y z 1 x y z 1 ROX ( ).
x x,
y y cos z sin ,
z y sin z cos .
0
1
0 cos
R
( )
OX
0 sin
0
0
0
sin
cos
0
0
0
.
0
1

9.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
1. Поворот относительно прямой (вокруг оси OY,
правосторонняя система).
x r cos( ) r cos cos r sin sin x cos z sin ,
z r sin( ) r sin cos r cos sin z cos x sin ;
z
M
r
M’
x
O
x y z 1 x y z 1 ROY ( ).
x x cos z sin ,
y y,
z x sin z cos .
cos
0
R
( )
OY
sin
0
0
1
0
0
sin
0
cos
0
0
0
.
0
1

10.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
1. Поворот относительно прямой (вокруг оси OZ,
правосторонняя система).
cos
sin
R ( )
oz
0
0
sin
cos
0
0
0
0
1
0
0
0
.
0
1

11.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
2. Растяжение/сжатие по осям.
x y z 1 x y z 1 D( , , ).
0
0
D( , , )
0
0
0
0
0 0
0 0
, , , 0.
0
0 1
– коэффициент растяжения (если >1) или сжатия (если <1)
по оси OX, >0.
– коэффициент растяжения (если >1) или сжатия (если <1)
по оси OY, >0.
– коэффициент растяжения (если >1) или сжатия (если <1)
по оси OZ, >0.

12.

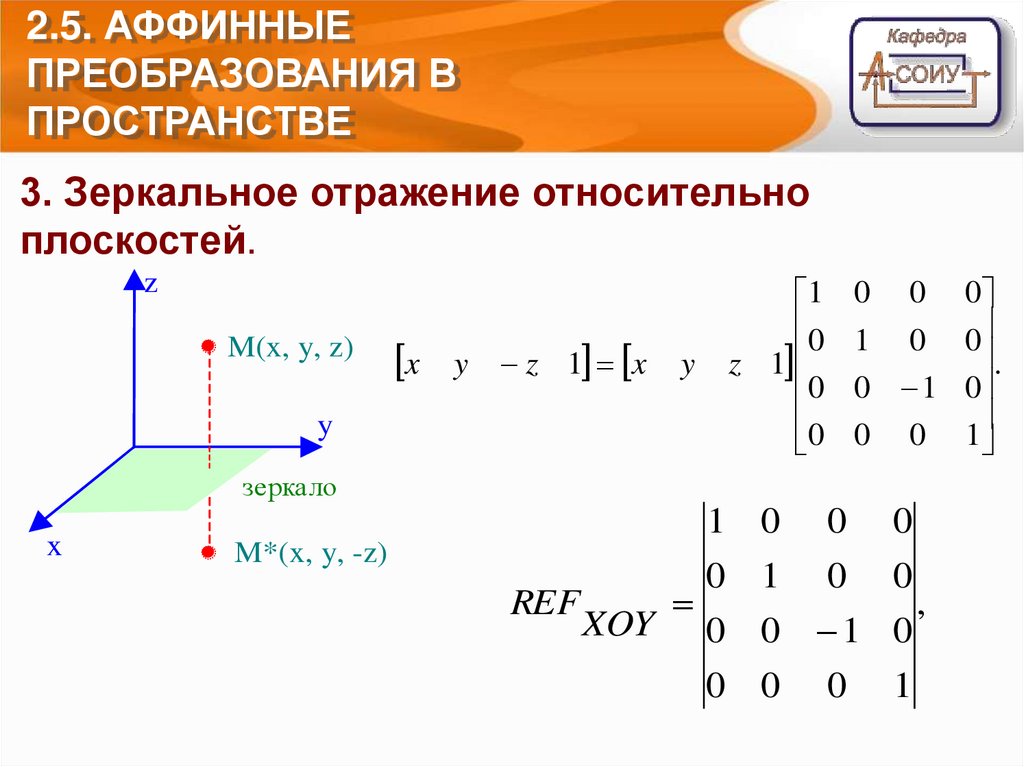
2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
3. Зеркальное отражение относительно
плоскостей.
z
M(x, y, z)
x
y
z 1 x
y
y
1
0
z 1
0
0
0 0
1 0
0 1
0 0
зеркало
x
M*(x, y, -z)
1
0
REF
XOY 0
0
0 0
1 0
0 1
0 0
0
0
,
0
1
0
0
.
0
1

13.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
3. Зеркальное отражение относительно
плоскостей.
1 0
0 1
REF
XOZ 0 0
0 0
0
0
1
0
0
0
,
0
1
1
0
REF
YOZ
0
0
0
1
0
0
0
0
1
0
0
0
,
0
1

14.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
4. Перемещение по вектору.
Пусть точка перемещается на вдоль оси OX, на
вдоль оси OY и на вдоль оси OZ (таким
образом, , , составляют элементы вектора
перемещения). И пусть старые координаты
равны (x, y, z, 1), тогда новые координаты будут
равны (x+ , y+ , z+ , 1)
x
y
z 1 x
y
1
0
z 1
0
0 0
0 0
.
1 0
1
0
1
0

15.

2.5. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ В
ПРОСТРАНСТВЕ
4. Перемещение по вектору.
1
0
T ( , , )
0
0
1
0
0 0
0 0
.
1 0
1

16.

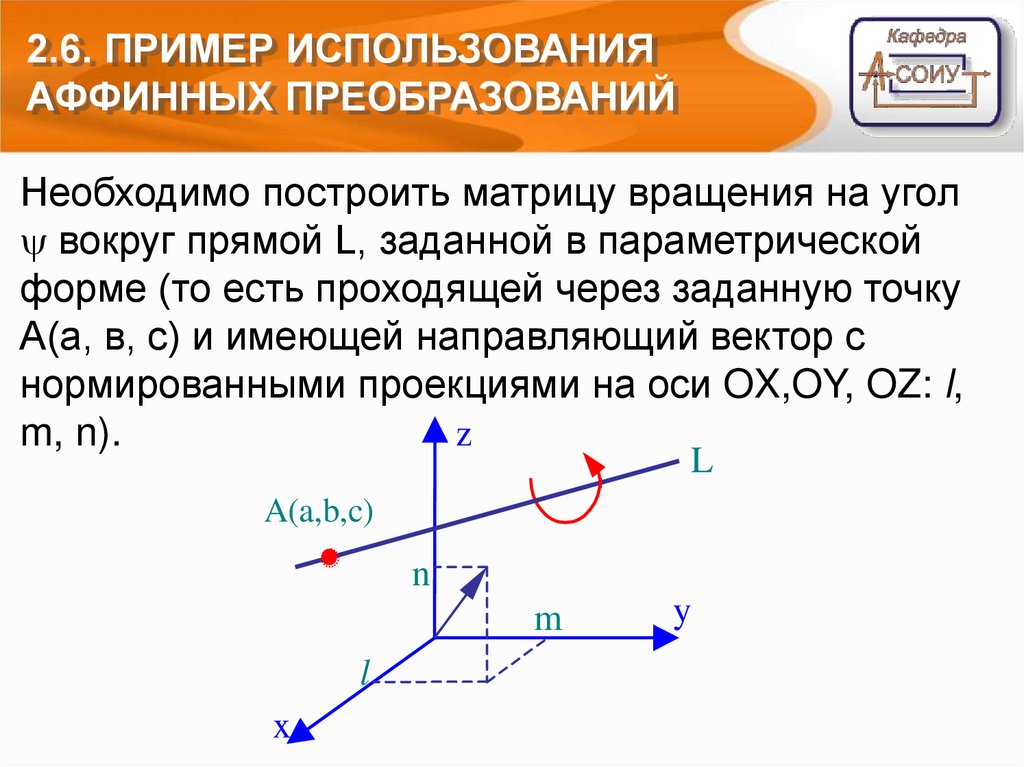
2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
Необходимо построить матрицу вращения на угол
вокруг прямой L, заданной в параметрической
форме (то есть проходящей через заданную точку
А(a, в, с) и имеющей направляющий вектор с
нормированными проекциями на оси OX,OY, OZ: l,
m, n).
z
L
A(a,b,c)
n
m
l
x
y

17.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
1) Перенос точки А в начало координат
z
L
A(a,b,c)
y
x

18.

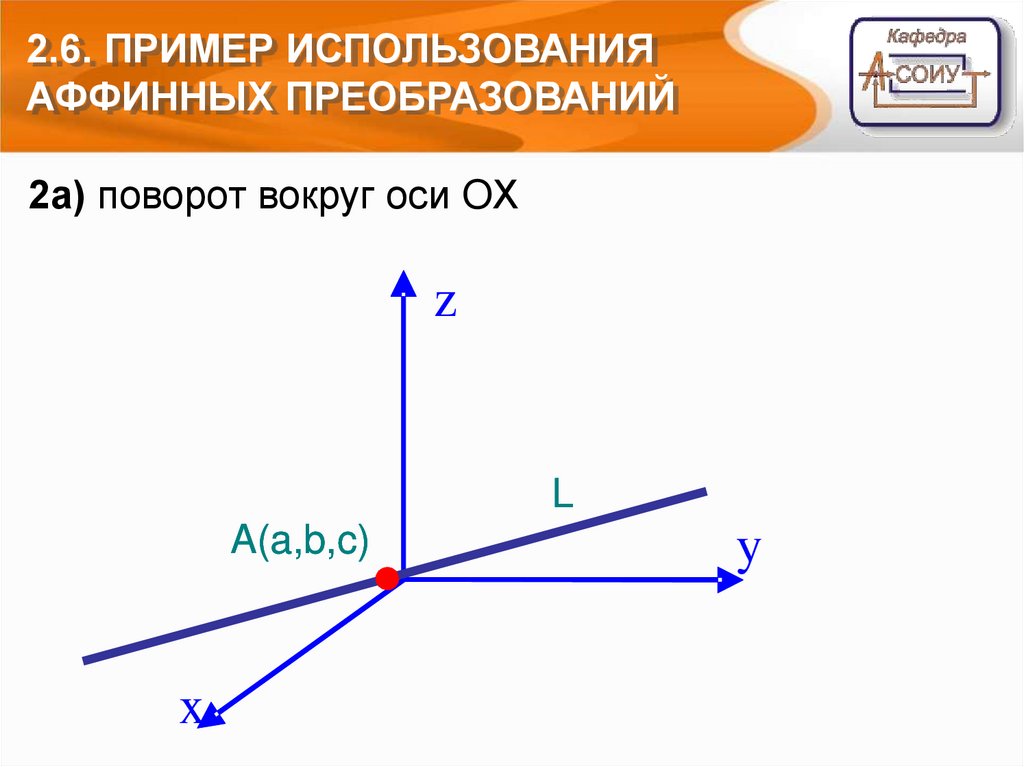
2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
2а) поворот вокруг оси OХ
z
L
A(a,b,c)
x
y

19.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
2б) поворот вокруг оси OY
z
y
x

20.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
3) Поворот вокруг OZ на заданный угол (цель
задачи)
Далее идут операции обратные операциям 1 и 2,
чтобы вернуть прямую в первоначальное
положение (уже с поворотом):
4а) поворот вокруг оси OY,
4б) поворот вокруг оси OХ,
5) возврат точки А в первоначальное положение.

21.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
Шаг 1. Перенос в начало координат точки А
задается матрицей:
1
0
0
0
1
0
T ( a, b, c)
0
0
1
a b c
0
0
.
0
1

22.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
Шаг 2. Конструирование двух поворотов.
Конструировать будем относительно конца (так как
результат известен).
cos
0
l m n 1
sin
0
[l’cos + n’sin
0
1
0
0
sin
0
cos
0
0
0
0
0
1
m’ -l’sin + n’cos
a) m’= 0;
б) l’cos + n’sin = 0;
в) -l’sin + n’cos = 1.
0 1 1 ,
1]
l’= -sin , n’= cos

23.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
Шаг 2. Конструирование двух поворотов.
1
0
0
0
0
l m n 1
0
0
l
cos
sin
0
m cos n sin
sin
cos
0
0
l 0 n 1 .
0
1
m sin n cos 1 l 0 n 1 .
а) l’ = l;
m
n
б) m cos – n sin = 0; cos , ; sin n , ;
n
в) m sin + n cos = n’.
m2 + n2 = n’2

24.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
cos
n
n2 m 2
cos m2 n2 ;
;
sin
m
n2 m2
;
sin l.
SCEN = T(-а,-b,-с) ROX( ) ROY( ) ROZ ( )
ROY (- ) ROX (- ) T(а,b,с)

25.

2.6. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
l 2 cos (1 l 2 )
l (1 cos )m n sin
l (1 cos )n m sin
l (1 cos )m n sin
m2 cos (1 m2 )
m(1 cos )n l sin
l (1 cos )n m sin
m(1 cos )n l sin .
n2 cos (1 n2 )