Радиотехническая система

1.

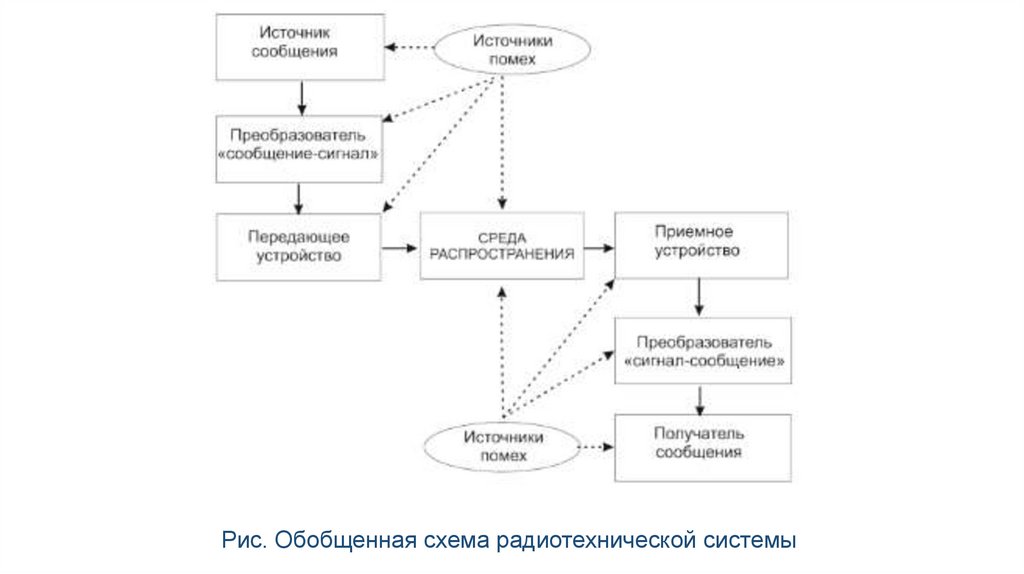
Рис. Обобщенная схема радиотехнической системы

2.

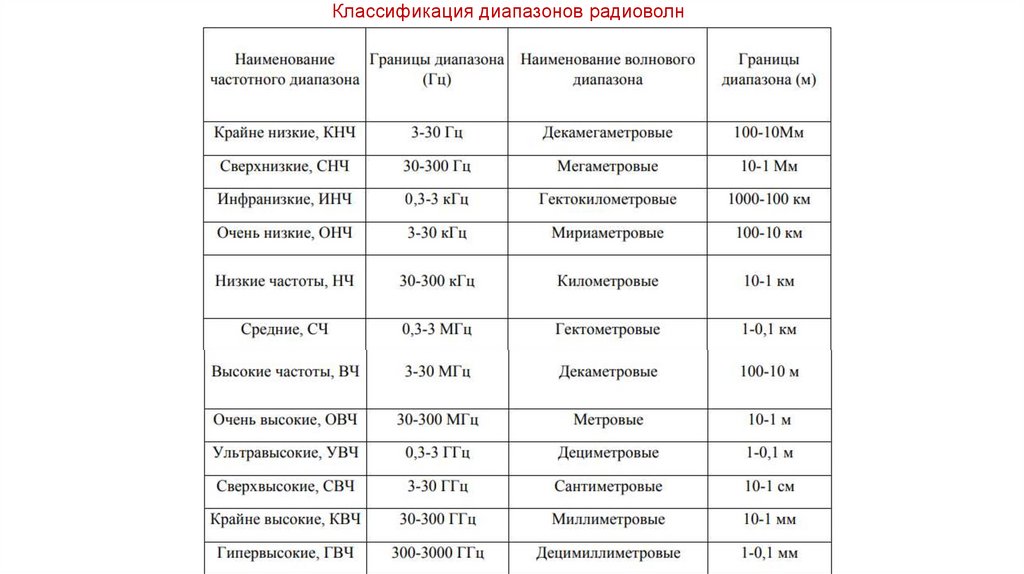
Классификация диапазонов радиоволн

3.

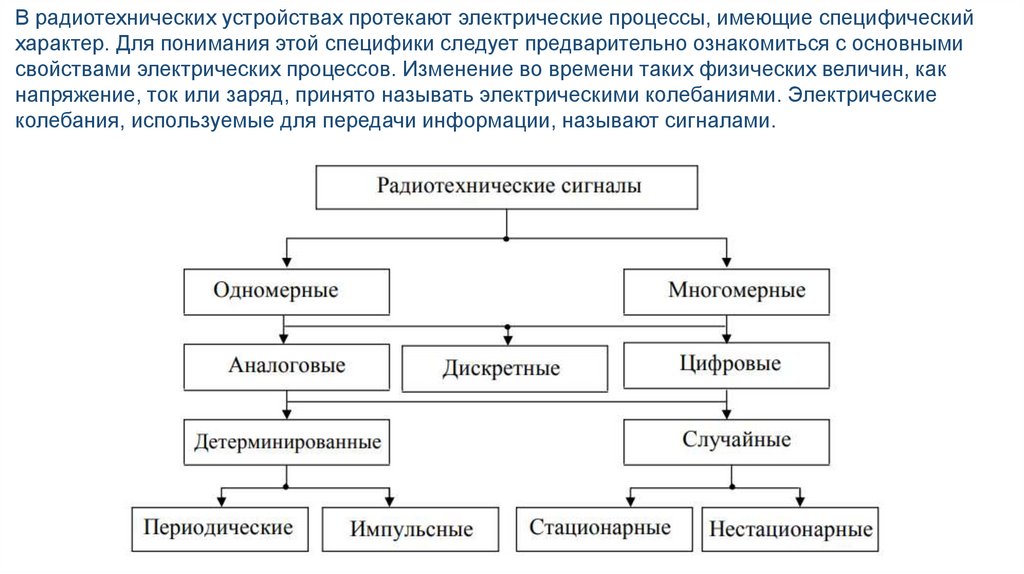
В радиотехнических устройствах протекают электрические процессы, имеющие специфический
характер. Для понимания этой специфики следует предварительно ознакомиться с основными
свойствами электрических процессов. Изменение во времени таких физических величин, как
напряжение, ток или заряд, принято называть электрическими колебаниями. Электрические
колебания, используемые для передачи информации, называют сигналами.

4.

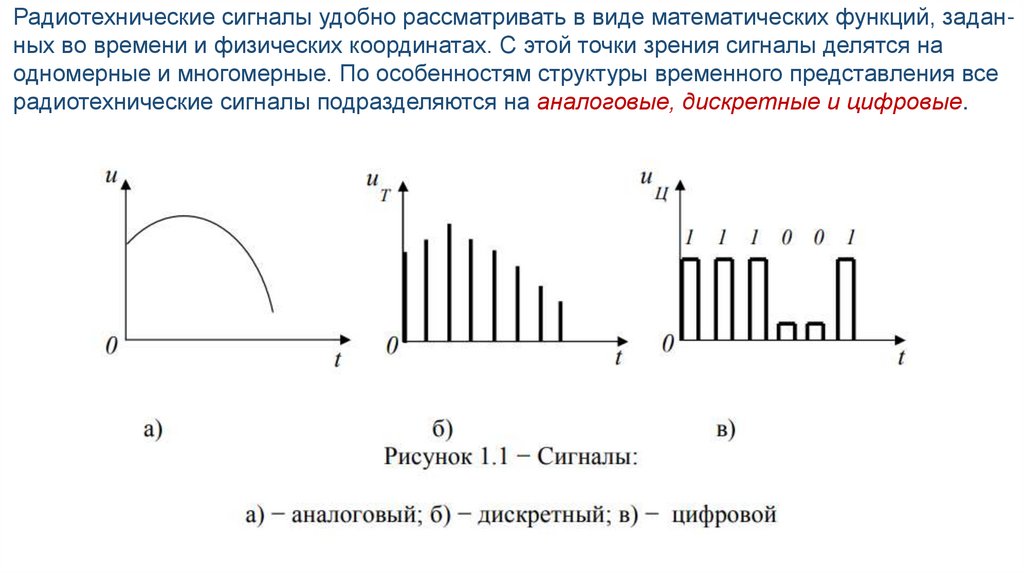
Радиотехнические сигналы удобно рассматривать в виде математических функций, заданных во времени и физических координатах. С этой точки зрения сигналы делятся на
одномерные и многомерные. По особенностям структуры временного представления все
радиотехнические сигналы подразделяются на аналоговые, дискретные и цифровые.

5.

Общие сведения о радиотехнических сигналах
При передаче информации на расстояние с помощью радиотехнических систем используются
различные виды радиотехнических (электрических) сигналов.
Радиотехническими сигналами принято считать любые электрические сигналы, относящиеся к
радиодиапазону. С математической точки зрения всякий радиотехнический сигнал можно
представить некоторой функцией времени u(t), которая характеризует изменение его мгновенных
значений напряжения (чаще всего), тока или мощности. По математическому представлению все
многообразие радиотехнических сигналов принято делить на две основные группы:
детерминированные (регулярные) и случайные сигналы.
Простейшая математическая модель дискретного сигнала u (t) T − это последовательность точек на
временной оси, в каждой из которых заданы значения соответствующего непрерывного сигнала.
Одной из разновидностей дискретных сигналов является цифровой сигнал. В цифровом сигнале
дискретные значения сигнала u (t) T заменяются числами uЦ (t) , чаще всего реализованными в
двоичном коде, который представляют высоким (единица) и низким (нуль) уровнями потенциалов
напряжения.
Детерминированными называют радиотехнические сигналы, мгновенные значения которых в
любой момент времени достоверно известны, т. е. предсказуемы с вероятностью равной
единице. Примером детерминированного радиотехнического сигнала может служить гармоническое
(синусоидальное) колебание, последовательность импульсов, форма, амплитуда и временное
положение которых заранее известно. Детерминированные сигналы можно подразделить на
периодические и непериодические (импульсные).

6.

Периодические сигналы бывают гармоническими, т. е. содержащими только одну
гармонику, и полигармоническими, спектр которых состоит из множества гармонических
составляющих.
К гармоническим сигналам относятся сигналы, описываемые функцией синуса или
косинуса. Все остальные сигналы являются полигармоническими.
Случайные сигналы − это сигналы, мгновенные значения которых в любые моменты
времени неизвестны и могут быть предсказаны лишь с некоторой вероятностью,
меньшей единицы. Практически все реальные случайные сигналы или большинство из
них представляют собой хаотические функции времени.
По сути дела детерминированный сигнал не несет в себе никакой информации и
практически все его параметры можно передать по каналу радиосвязи одним или
несколькими кодовыми значениями. Другими словами, детерминированные сигналы
(сообщения) по существу не содержат в себе информации, и нет смысла их передавать.
Сигналом, несущим полезную информацию, может быть только случайный сигнал. В
процессе передачи информации сигналы подвергаются тому или иному преобразованию,
например модуляции, демодуляции (детектированию), кодированию (декодированию),
усилению, задерживанию, и др.

7.

Периодические сигналы
Периодическим называется любой сигнал, для которого выполняется условие
u (t ) = u (t + nT ),
где период повторения или следования импульсов T , a n − любое целое число.
Простейшим периодическим детерминированным сигналом является гармоническое
колебание (ток, напряжение, заряд, напряженность поля), определяемое законом
u(t) = A cos (2π t / T + ϑ) = A cos (ωt + ϑ ), - ∞ < t < ∞ (1.1) ,
где A, T, ω и ϑ − постоянные амплитуда, период, угловая частота и начальная фаза
колебания.
Любой сложный периодический сигнал, как известно, можно представить в виде суммы
гармонических колебаний с частотами, кратными основной частоте ω = 2π t / T .
Основной характеристикой сложного периодического сигнала является его
спектральная функция, содержащая информацию об амплитудах и фазах отдельных
гармоник.

8.

По особенностям структуры временного представления все радиотехнические
сигналы делятся на непрерывные и дискретные, а по типу передаваемой информации:
на аналоговые и цифровые.
В радиотехнике широко применяются импульсные системы, действие которых основано
на использовании дискретных сигналов. Одной из разновидностей дискретных сигналов
является цифровой сигнал. В нем дискретные значения сигнала заменяются числами,
чаще всего реализованными в двоичном коде, который представляют высоким (единица)
и низким (нуль) уровнями потенциалов напряжения.
Функции, описывающие сигналы, могут принимать как вещественные, так и комплексные
значения. Поэтому в радиотехнике говорят о вещественных и комплексных сигналах.
Применение той или иной формы описания сигнала дело математического удобства.

9.

Понятие спектра
Непосредственный анализ воздействия сигналов сложной формы на радиотехнические
цепи весьма затруднителен и вообще не всегда возможен. Поэтому сложные сигналы
имеет смысл представлять как сумму некоторых простых элементарных сигналов.
Принцип суперпозиции обосновывает возможность такого представления, утверждая, что
в линейных цепях воздействие суммарного сигнала равносильно сумме воздействий
соответствующих сигналов по отдельности.
В технике широко используются резонансные системы, позволяющие экспериментально
выделять одну гармонику из сложного сигнала.
Представление сигнала суммой гармоник, заданных частотой, амплитудой и фазой,
называется разложением сигнала в спектр.
Гармоники, входящие в состав сигнала, задаются в тригонометрической или мнимопоказательной форме.

10.

Спектр периодического сигнала
Рассмотрим общие свойства спектров периодических сигналов. Если сигнал V(t) периодичен с
периодом Т, то он разлагается в ряд Фурье согласно соотношениям:
Из приведенных соотношений видно:
а) Перемещение оси абсцисс вверх или вниз равносильно прибавлению некоторой постоянной величины ко всем значениям V(t).
Такое преобразование изменяет среднее значение - постоянную составляющую a0 , и не влияет на амплитуды и фазы гармоник. Т
ак можно утверждать, что, например, спектр сигналов, приведенных на рис. 1, отличается только постоянной составляющей.
Заштрихованные площади должны быть равными, тогда a0 - среднее значение.

11.

Рис.1. Сигналы, отличающиеся только величиной ао
б) Спектр периодического сигнала дискретен, он состоит из гармоник с частотами f=n/T, где n -любое целое
число, f в герцах. Никаких других частот, кроме данных в периодическом сигнале быть не может, но вовсе не
обязательно, чтобы в каждом конкретном сигнале существовали все возможные составляющие: для некоторых
гармоник часть коэффициентов Ai и Bi может обращаться в ноль, т. е. соответствующие гармоники отсутствуют.

12.

Иногда обращение в ноль части гармоник можно увидеть непосредственно по форме сигнала без обращения к формулам:
1) Если сигнал представляет собой гармонику, то, естественно, в его составе нет никаких других гармоник, и он характеризуется только одной
частотой.
2) Если при соответствующем выборе начала отсчета времени сигнал представляет собой четную функцию,
т. е. V(t)=V(-t), то в соотношениях (1.2.): V(t)Sin(wit)- нечетная функция (Sin -нечетная), а V(t)Cos(wit) - четная функция.
т. е. сигналы разлагаются только по косинусам. Физически это означает, что в точке принятой за начало отсчета, все
гармоники одновременно имеют экстремум: Максимум, если окажется положительным, и минимальным, если
- отрицательным. На рис. 2 приведены примеры таких сигналов. На рисунке Т1-длительность импульса t:

13.

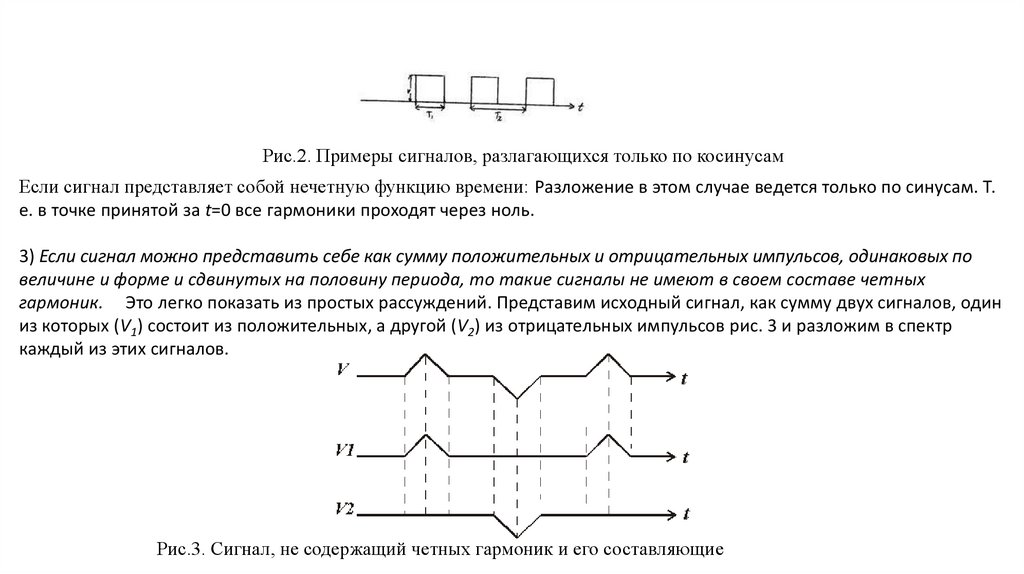
Рис.2. Примеры сигналов, разлагающихся только по косинусам
Если сигнал представляет собой нечетную функцию времени: Разложение в этом случае ведется только по синусам. Т.
е. в точке принятой за t=0 все гармоники проходят через ноль.
3) Если сигнал можно представить себе как сумму положительных и отрицательных импульсов, одинаковых по
величине и форме и сдвинутых на половину периода, то такие сигналы не имеют в своем составе четных
гармоник. Это легко показать из простых рассуждений. Представим исходный сигнал, как сумму двух сигналов, один
из которых (V1) состоит из положительных, а другой (V2) из отрицательных импульсов рис. 3 и разложим в спектр
каждый из этих сигналов.
Рис.3. Сигнал, не содержащий четных гармоник и его составляющие

14.

Сигналы V1 и V2 имеют одинаковый период, величину и форму, поэтому входящие в их состав гармоники будут иметь
одинаковые частоты и амплитуды. Что касается фазовых соотношений, то тут ситуация для четных и нечетных
гармоник различна. Для четных гармоник сдвиг фаз на полпериода основной частоты соответствует сдвигу на целое
число периодов рассматриваемой гармоники, т. е. не меняет ее фазу. Таким образом, фазы четных гармоник,
составляющих V1 и V2 оказываются противоположными (импульсы противоположной полярности) и
соответствующие гармоники компенсируются, т. е. они отсутствуют в суммарном сигнале V. Для нечетных гармоник
сдвиг фаз на полпериода основной частоты соответствует сдвигу фаз на целое число периодов плюс еще полпериода
частоты данной гармоники, что изменяет фазу на π.
C учетом противоположной полярности импульсов эти гармоники оказываются в фазе и их амплитуды удваиваются
при сложении.

15.

Мы отмечали, что смещение оси абсцисс вверх или вниз меняет только постоянную составляющую сигнала. Поэтому,
проверяя сигнал на наличие четных гармоник, можно мысленно осуществлять такое смещение. На рис. 4 приведены
еще два сигнала, не содержащие четных гармоник:
Рис.4. Примеры сигналов, не содержащих четных гармоник
В первом сигнале условием отсутствия четных гармоник является то, что длительность должна быть в два раза
меньше периода. Во втором случае время возрастания и убывания напряжения должны быть равны. Тогда при
смещении оси времени на высоту, равную среднему значению сигнала, мы получим, что части сигнала,
расположенные по разные стороны оси равны и смещены относительно друг друга на половину периода.
Следовательно, как было рассмотрено ранее, получается обнуление каждой четной гармоники за счет «разно
полярности» этих частей сигнала.

16.

в) Количество гармоник в ряде Фурье теоретически бесконечно и полоса частот, которую он занимает, не ограничена
сверху. Однако так как общая мощность сигнала всегда ограничена, то для всех реальных сигналов существует
тенденция к постепенному уменьшению амплитуд гармоник по мере увеличения их номера. Соответственно при
передаче сигнала с заданной степенью точности можно пренебрегать высокими, достаточно слабыми гармониками, не
передавать их, ограничивая полосу пропускания сверху. Требования к полосе частот зависят от типа сигнала и
заданного уровня точности его воспроизведения

17.

2. Спектр периодической последовательности прямоугольных импульсов
Рассмотрим периодическую последовательность прямоугольных импульсов, изображенную на рис. 5. Данный
сигнал характеризуется длительностью импульса, его амплитудой и периодом. По вертикальной оси откладывается
напряжение.
Рис.5. Периодическая последовательность прямоугольных импульсов
Начало отсчета выберем в середине импульса. Тогда сигнал разлагается только по косинусам. Частоты гармоник
равны n/T , где n - любое целое число.
зависимость амплитуды n-ой гармоники от периода и длительности в виде непрерывной функции (функция
Эту функцию называют огибающей спектра. Следует иметь ввиду, что физический смысл она имеет только на частотах,
где существуют соответствующие гармоники. На рис. 6 приведен спектр периодической последовательности
прямоугольных импульсов.

18.

Рис.6. Спектр периодической последовательности прямоугольных импульсов.
получается квазиосцилирующая функция с постепенным убыванием.
Огибающая ограничивает на графике амплитуды гармоник. Форма огибающей определяется формой и
длительностью импульса, а частоты гармоник только его периодом /2/.
Это утверждение, полученное для прямоугольных импульсов справедливо и для других периодических сигналов.

19.

5. Спектры модулированных колебаний
Колебания с широким спектром, в состав которых входят гармоники, сильно отличающиеся по частоте, нельзя
передавать в эфир: разные гармоники будут распространяться по-разному, их фазовые и амплитудные соотношения
изменятся и сигнал исказится до неузнаваемости. Кроме того, низкие частоты вообще очень сложно передавать в
эфир. Поэтому в радиотехнике широко применяются модулированные колебания. Это колебания
квазигармонические, похожие на гармонику, но какой-то их параметр изменяется под действием передаваемого
сигнала /2/. Наиболее распространенными видами модуляции являются амплитудная (АМ) и частотная (ЧМ).

20.

6. Спектр амплитудно-модулированных колебаний
Рассмотрим сначала простейший случай, когда модуляция амплитуды происходит по
гармоническому закону:
W - частота модулирующего сигнала
w0 -частота несущей
Рис.9. Спектр квазигармонического колебания, амплитудно модулированного гармоникой

21.

Частным случаем АМ сигнала является одиночный радиоимпульс. Пример такого импульса изображен на рис. 10.
Сверху изображен радиоимпульс и, соответственно, его спектр, снизу – прямоугольный модулирующий импульс со
своим спектром. Рассмотрим рисунок:
Рис.10. Прямоугольный (а) радиоимпульс и соответствующий ему модулирующий импульс и их спектры

22.

Можно считать, что такой радиоимпульс представляет собой гармонику с частотой w0, модулированную по амплитуде
одиночным прямоугольным импульсом (на том же рисунке).
Спектр прямоугольного импульса был рассмотрен ранее. Учитывая свойства АМ сигналов, можно видеть:
радиоимпульс имеет непрерывный спектр, симметричный относительно несущей w0. Поскольку импульсы одиночные,
они характеризуются спектральной плотностью, а не амплитудами отдельных гармоник.

23.

7. Спектр частотно-модулированных колебаний
Рассмотрим опять случай модуляции гармоническим сигналом. Тогда мгновенная частота:
δw - девиация частоты, т. е. максимальное отклонение мгновенной частоты от средней. Чтобы колебания были
близки к гармоническим надо, чтобы частота изменялась медленно и не слишком сильно, т. е. необходимо, чтобы:
Величина m (глубина или индекс частотной модуляции) может быть как меньше, так и больше единицы. Тогда для
ЧМ колебания:

24.

Рис. 11. функции Бесселя

25.

Характер спектра при частотной модуляции сильно зависит от глубины модуляции. При m<<1, т. е. бw<<W
модуляцию называют узкополосной.
Амплитуды остальных гармоник пренебрежимо малы. Поэтому: при узкополосной ЧМ в спектре присутствуют, как
и при АМ, три частоты: w0; w0 +W; w0 -W. Фазовые отношения при ЧМ отличаются от АМ.
Когда m>>1 (бw<<W), то модуляция называется широкополосной. Действительно, при такой модуляции полоса частот,
занимаемая ЧМ сигналом много шире, чем при АМ. Считается, что по обе стороны от несущей существенную
амплитуду имеют по (m+1) гармоник.
Сохраняются и выражения: узкополосная и широкополосная ЧМ.

26.

существует два практически важных класса задач, в которых применение понятия спектра позволяет находить решение наиболее легко и наглядно:
Первый случай - это задачи, в которых рассматриваемая линейная цепь представляет собой резонансную систему, настроенную на одну из сильнейших
гармоник входного сигнала. Тогда, практически, только эта гармоника и проходит на выход. Все остальные ослабляются настолько сильно,
что в выходном сигнале ими можно пренебречь. Тогда для определения формы выходного сигнала никакие расчеты не нужны. Можно сразу утверждать,
что выходной сигнал - гармонический и имеет частоту резонансной гармоники, поскольку только эта гармоника и проходит на выход. Для определения
амплитуды этой гармоники достаточно, очевидно, определить ее амплитуду на входе (из разложения в спектр), а затем умножить ее на коэффициент
передачи на резонансной частоте.
2) Второй случай, часто встречающийся в технике: нужно сформулировать требования к цепи, чтобы через нее можно было пропускать заданный
сигнал при допустимом уровне искажений.
Здесь тоже нет необходимости суммировать гармоники для определения формы выходного напряжения - оно должно повторять входное. задача
фактически сводится к определению полосы
частот, занятой сигналом. Тогда используемая цепь должна равномерно (с постоянным коэффициентом передачи) пропускать все частоты
внутри этой полосы.

27.

Однако, как мы видели, большая часть сигналов имеет теоретически неограниченный спектр. Практически всегда
полоса сигнала считается ограниченной областью наиболее сильных гармоник, слабыми гармониками пренебрегают
и на выход их не передают. Вопрос в том, какие гармоники считать слабыми, не является однозначным. Ответ на
него зависит от того, с какой точностью необходимо воспроизводить сигнал. Например, при передаче цифрового
кода форма импульса не несет информации, важно только надежно регистрировать приход импульса. Поэтому, если
спектральная плотность уменьшается по сравнению с максимальной в 3-4 раза, то можно не пропускать на выход
соответствующую область частот.
Наоборот, если важно как можно точнее воспроизвести форму сигнала, полосу пропускания нужно увеличить.
В целом, нужно отметить, что более широкая полоса пропускания требуется для передачи коротких импульсов с
крутыми фронтами.

28.

Разложение сложных периодических сигналов на гармонические составляющие.
При разложении периодического колебания s (t) в ряд Фурье по тригонометрическим
функциям в качестве ортогональной системы берут
Интервал ортогональности в совпадает с периодом ω = 2π t / T = 2π / ω1 функции s (t).
Спектральную составляющую с частотой ω1 называют первой (основной) гармоникой, а
составляющие с частотами n ω1 (n > 1) − высшими гармониками периодического
сигнала.

29.

где:
Спектральную составляющую с частотой ω1 называют первой (основной) гармоникой, а
составляющие с частотами nω1 (n > 1) −высшими гармониками периодического
сигнала.

30.

С математической точки зрения часто удобно выражение (1.4) описывающее данный
сигнал, представлять в другой, эквивалентной форме ряда Фурье:

31.

Спектр периодического сигнала принято называть линейчатым или дискретным, так как он состоит из отдельных
линий, высота которых равна амплитуде Аn соответствующих гармоник. На рисунке 1.2 приведены спектры
периодического сигнала: а) − амплитудный; б) − фазовый; в) – комплексный.
Рисунок 1.2 – Спектры периодических сигналов: а) −
амплитудный; б) − фазовый; в) – комплексный