Фундаментальная формула Грина. Лекция 14

1.

Фундаментальная формула Грина.
Лекция 14
Лектор Исаева Л.Д.

2.

План лекции
• Фундаментальная формула Грина.

3.

• Фундаментальная формула Грина получается из
второй его формулы при значениях:
dV
(
)dS
n
n
V
S
• =U , = V= 1/r ,
• где r - расстояние от элементов объема d и
поверхности dS до точки Р, в которой
рассматривается функция U. Тогда вторая
формула Грина записывается в таком виде:
1 1
1 1 U
v U r r U d S U n r r n dS
• Рассмотрим три случая полученного
равенства (1).

4.

5.

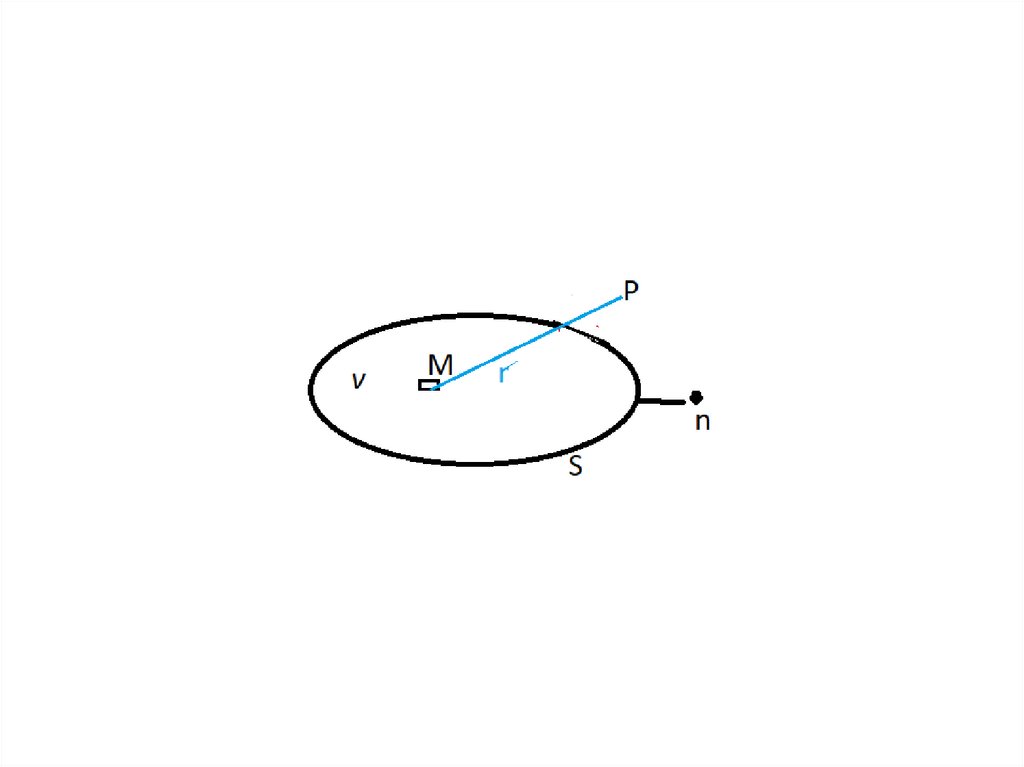
• 1) Точка Р лежит вне поверхности S в области V1. В
этом случае во всех внутренних точках М
функция
1/r – удовлетворяет уравнению Лапласа.
2
x
x
y
y
z
z
1
3
3
3
r
0
0
0
3 3
3 5 0
5
r
r r
r r
2
2
2
• Учитывая это равенство, из (1) уравнения получим(2):
v
1
1 U
1
Ud
dS U dS 0.
r
r n
n r
S
S

6.

7.

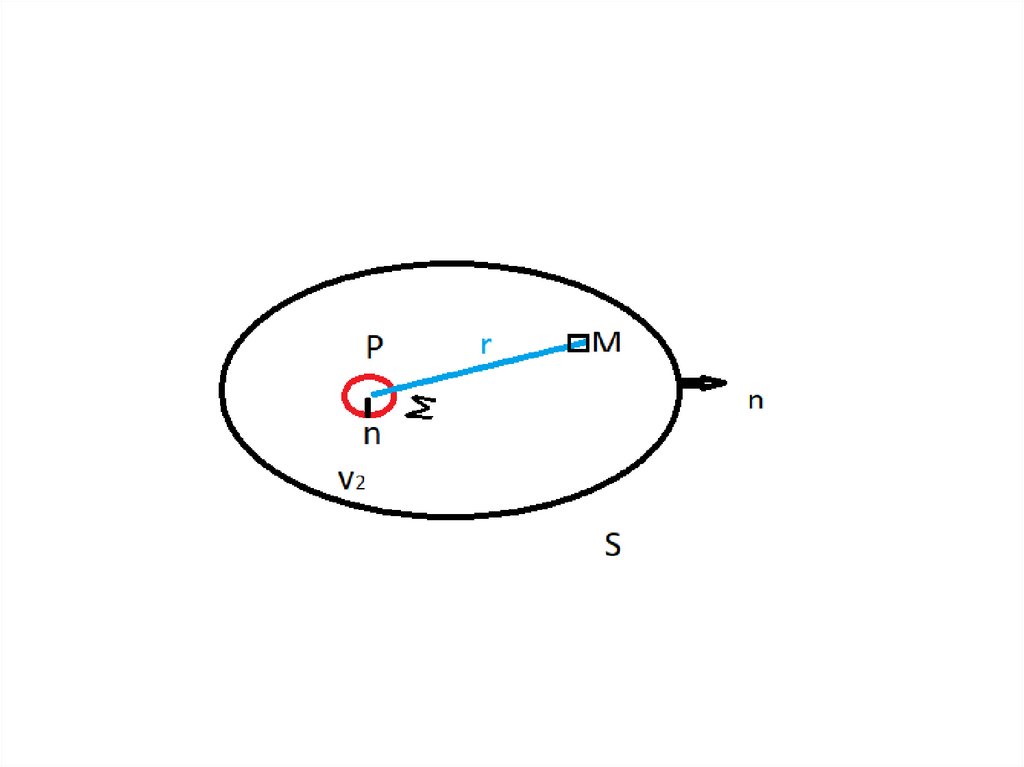
• 2) Точка Р лежит внутри области V (т.е. внутри S). Тогда
формулу Грина нельзя применять ко всей области V, т.к.
в точке М, когда она совпадает с точкой Р, функция 1/r –
терпит разрыв (r→0, 1/r→
).
Поэтому окружим точку
Р некоторой сферой ∑. В этом случае вне поверхности в
области V снова можно применять формулу Грина.
Применяя ее, получим (3):
2
1
1 U
1
1
1 U
Ud
dS U dS U dS
dS .
r
n r
n r
r n
S r n
S
• Где V2 – область V, за исключением ее части,
ограниченной поверхностью ∑, а поверхностные
интегралы берутся сразу по двум поверхностям S и ∑ в
области V2. При бесконечном сжатии поверхность ∑
стягивается к точке Р

8.

• В этом случае, интеграл по объему V2 будет
стремиться к интегралу по объему V:
1
lim Udv 1r Udv
v2 r
v
0
• Рассмотрим значения последних двух
интегралов из (3) выражения(4)
1 U
1
1 U
1
dS U dS
dS U dS .
r n
n r
r r
r r

9.

• Здесь внешняя нормаль по отношению к объему V2 для
поверхности ∑ является внутренней , поэтому при
интегрировании по поверхности ∑ :
1
1
;
n r
r r
U
U
;
n
r
• в пределе первый интеграл (4) выражения дает:
1
U
1
U
U
1
2
U
dS
dS
dS
4
r
4 U P
lim
lim
lim
lim
2
2
2
2
r
r r
0 r r
0 r
0 r
0 r
'
• Подставляя полученные значения рассмотренных
интегралов в уравнении(3) получим(5)
v
1
1 U
1
Ud
dS U dS 4 U P .
r
r n
n r
S
S

10.

11.

• 3) Точка Р лежит на поверхности S. В этом случае
рассуждая также , как и выше получим соотношение,
аналогичное (5), в правой части будет величина 2 U P .
• Это связано с тем, что когда точка находится на
поверхности интеграл берется оп полуcфере.
• Объединив все три рассмотренных случая, окончательно
получим[6]:
0, 1 ,
1
1 U
1
Ud
dS U
dS 2 U P , S
r
r n
n r
S
S
4 U P , .
• Данная формула называется фундаментальной
формулой Грина.

12.

В фундаментальной формуле Грина (6) произведем
некоторые обозначения:
1- интеграл является потенциалом притяжения
объемных масс, если их плотность в каждой точке М
объема v равна σ = U M
2- интеграл есть потенциал притяжения простого слоя,
если величина U
n
равна плотности распределения масс на поверхности.
3- интеграл является потенциалом притяжения двойного
слоя, величина момента которого в каждой точке М на
поверхности S равна U. β= U.
Таким образом, в левой части фундаментальной формулы
Грина находится сумма потенциалов притяжения трех
видов: объемных масс, простого слоя и двойного слоя.

13.

• Частные случаи. 1. Если функция гармоническая, т.е. ,
формулу можно переписать:
1 U
1 =
s r n dS s U n r dS
0, P 1 ,
2 U P , P S
4 U P , P
• 2. Допустим: U 1 тогда , уравнение имеет вид
1
S n r dS
=
0, P 1 ,
2 , P S
4 , P
• Формула является формулой Гаусса. Подынтегральное
выражение имеет геометрический смысл. Оно
определяет величину элементарного телесного угла,
угла видимости, элемента поверхности dS из точки Р.

14.

Контрольные вопросы
• Поличение фундаментальной формулы
Грина .
• Смысл каждой составляющей
фундаментальной формулы Грина.