Похожие презентации:
Численные методы вычисления определенных интегралов
1. Лекция № 5 Численные методы вычисления определенных интегралов
2.
Численные методы вычисленияопределенных интегралов
Формула Ньютона-Лейбница
b
I f ( x)dx F (b) F (a)
a
Имеет ограниченное применение.
3.
1) Не каждая подынтегральная функция имеетпервообразную F(x).
«Неберущиеся» интегралы:
e
x2
sin x
dx, sin x dx, cos x dx,
dx,.....
x
2
2
2) Невозможно вычислить интеграл от
табличной функции.
Геометрический смысл определенного
интеграла:
Площадь криволинейной трапеции,
ограниченной осью ОХ, функцией f(x) и
прямыми: x=a и x=b.
4.
Отрезок [a,b] делят на n частей –элементарных отрезков. Такое деление
называется сеткой, а точки x0,x1,…,xn –
узлы сетки.
5.
Если сетка равномерная:b a
h
шаг сетки (шаг интегрирования )
n
Координата i го узла :
xi a i h, i 0,..., n
f ( xi ) f i
6.
Площадь криволинейной трапеции состоит изn-1 площадей элементарных трапеций Si.
(элементарных площадей). Интеграл
заменяют суммой площадей элементарных
трапеций.
b
n 1
a
i 0
I f ( x)dx Si
Численные методы интегрирования основаны на
различных способах оценки элементарных
площадей Si.
7.
Простейшие методы численногоинтегрирования. Методы
прямоугольников и трапеции.
1. Формулы прямоугольников.
А) Формула левых прямоугольников.
Рассмотрим элементарную трапецию Si.
8.
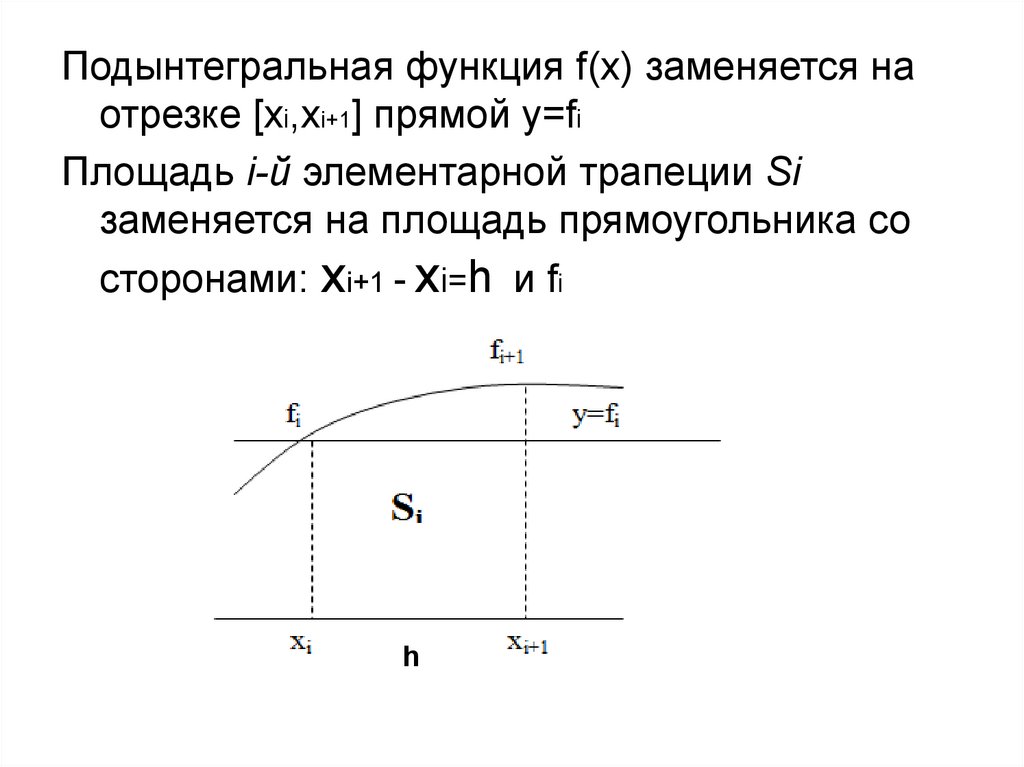
Подынтегральная функция f(x) заменяется наотрезке [xi,xi+1] прямой y=fi
Площадь i-й элементарной трапеции Si
заменяется на площадь прямоугольника со
сторонами: xi+1 - xi=h и fi
h
9.
Тогда Si f i hи
значение
интеграла
вычисляется по формуле левых прямоуголь ников :
n 1
n 1
n 1
n 1
i 0
i 0
i 0
i 0
I Si f i h h f i h f ( xi )
n 1
h f ( a i h)
i 0
10.
n 1I h f ( a i h)
i 0
11.
Б) Формула правых прямоугольниковПодынтегральная функция f(x) заменяется на
отрезке [xi,xi+1] прямой y=fi+1
Площадь i-й элементарной трапеции Si
заменяется на площадь прямоугольника со
сторонами: xi+1 - xi=h и fi+1
12.
Тогда Si f i 1 hи
значение
интеграла
вычисляется по формуле правых прямоуголь ников :
n 1
n 1
n 1
n 1
i 0
i 0
i 0
i 0
I Si f i 1 h h f i 1 h f ( xi 1 )
n
n
i 1
i 1
h f ( xi ) h f (a i h)
13.
nI h f ( a i h)
i 1
14.
В) Формула центральных прямоугольниковПодынтегральная функция f(x) заменяется на отрезке
[xi,xi+1] прямой
~
~
h
y f i , где f i f ( xi ) значение
2
функции в середине элементарного отрезка
15.
Площадь i-й элементарной трапеции Siзаменяется на площадь прямоугольника со
сторонами:
~
xi 1 xi h и f i
~
Тогда Si f i h
и
значение
интеграла
вычисляется по формуле центральных прямоуголь ников :
n 1
n 1
n 1
~
~
h
I Si f i h h f i h f ( xi )
2
i 0
i 0
i 0
i 0
n 1
n 1
h
h f (a i h )
2
i 0
16.
n 1h
I h f (a i h )
2
i 0
17.
Примечание.Для оценки точности необходимо использовать
способ двойного пересчета: увеличить число
разбиений (число элементарных отрезков) n
вдвое по сравнению с тем при котором
вычисляли значение интеграла, и найти
новое значение интеграла.
Если потребуется уменьшать шаг сетки до тех
пор, пока не будет выполняться неравенство:
I (h) I ( h2 ) ,
где ε - требуемая точность.
18.
Пример. Найти приближенное значениеопределенного интеграла
2
( x 1)dx
2
0,5
Решение:
1) Выбрать число отрезков (n)
2) Найти шаг интегрирования (h)
3) Выбрать приближенную формулу
19.
1) Пусть число отрезков n=52) Тогда шаг интегрирования
h=(b-a)/n=(2-0,5)/5=0,3
Узлы интегрирования:
20.
3) Формула левых прямоугольников.Подынтегральная функция f ( x) x 1
2
n 1
4
i 0
i 0
I h f (a i h) 0,3 f (0,5 i 0,3)
0,3 [ f (0,5) f (0,8) f (1,1) f (1,4) f (1,7)]
0,3 11,95 3,585
21.
Формула правых прямоугольников.n
5
i 1
i 1
I h f (a i h) 0,3 f (0,5 i 0,3)
0,3 [ f (0,8) f (1,1) f (1,4) f (1,7) f (2)]
0,3 15,7 4,71
22.
Формула центральных прямоугольников.n 1
4
h
I h f (a i h ) 0,3 f (0,5 i 0,3 0,15)
2
i 0
i 0
0,3 [ f (0,65) f (0,95) f (1,25) f (1,55) f (1,85)]
0,3 13,7125 4,11375
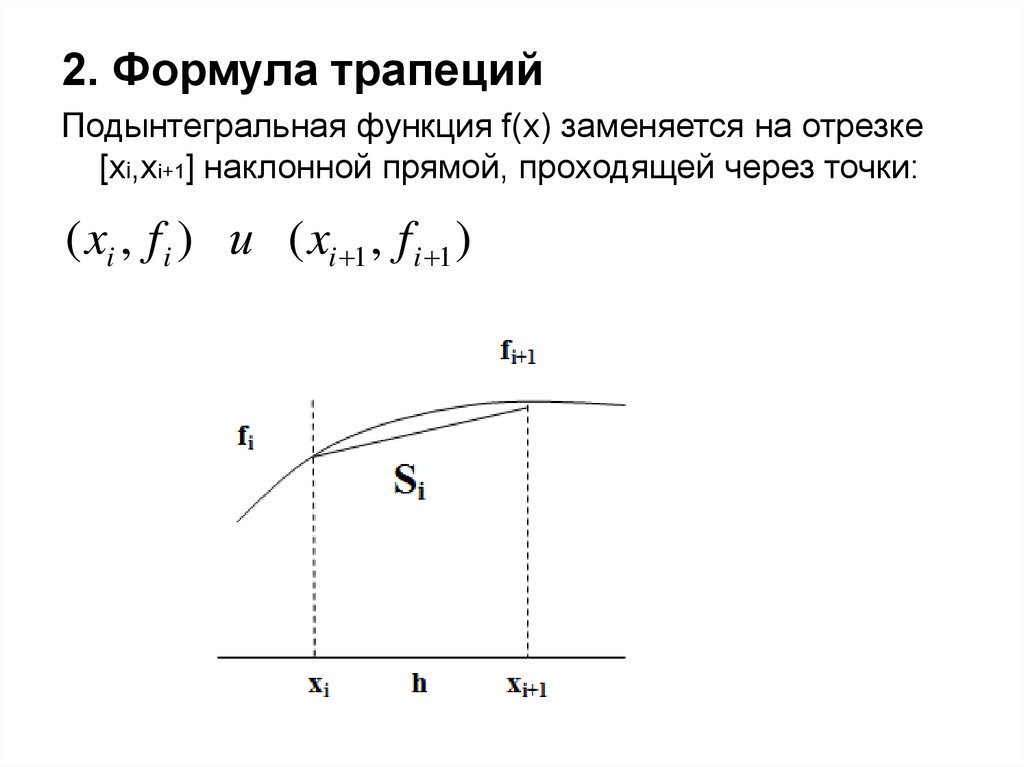
23.
2. Формула трапецийПодынтегральная функция f(x) заменяется на отрезке
[xi,xi+1] наклонной прямой, проходящей через точки:
( xi , f i ) и ( xi 1 , f i 1 )
24.
Площадь i-й элементарной трапеции Siзаменяется на площадь трапеции с
основаниями fi и fi+1 и высотой h=xi+1-xi
f i f i 1
Тогда Si
h и
значение
2
вычисляется по формуле трапеций :
интеграла
f i f i 1
I Si
h
2
i 0
i 0
f 0 f1 f1 f 2
f n 2 f n 1 f n 1 f n
h (
...
)
2
2
2
2
f 0 f n f1 f1
f n 1 f n 1
h (
...
)
2
2 2
2
2
n 1
n 1
25.
f 0 f n n 1h (
fi )
2
i 1
f (a ) f (b) n 1
h (
f ( a i h )) I
2
i 1
26.
f (a ) f (b)I h (
f ( a i h ))
2
i 1
n 1
27.
Пример.2
2
(
x
1)dx
0,5
Подынтегральная функция f ( x) x 2 1;
n 5, h 0,3
f (a) f (b) n 1
I h [
f (a i h)]
2
i 1
f (0,5) f (2) 4
0,3 [
f (0,5 i 0,3)]
2
i 1
f (0,5) f (2)
0,3 [
f (0,8) f (1,1) f (1,4) f (1,7)]
2
0,3 13,825 4,1475
28.
Формула Симпсона.Подынтегральная функция f(x) заменяется на
отрезке [xi,xi+1] параболой, проходящей через
3 точки (через крайние точки интервала и его
середину)
29.
Формула Симпсонаh f (b) f (a) n 1
h
I
f ( a i h) 2 f ( a i h )
3
2
2
i 0
30.
Пример.2
2
(
x
1)dx
0,5
Подынтегральная функция f ( x) x 1;
2
2 0,5
n 2, h
0,75
2
31.
По формуле Симпсона находимзначение интеграла :
0,75 f (2) f (0,5)
I
[
3
2
1
0,75
) ]
f (0,5 i 0,75) 2 f (0,5 i 0,75
2
i 0
0,25 16,5 4,125











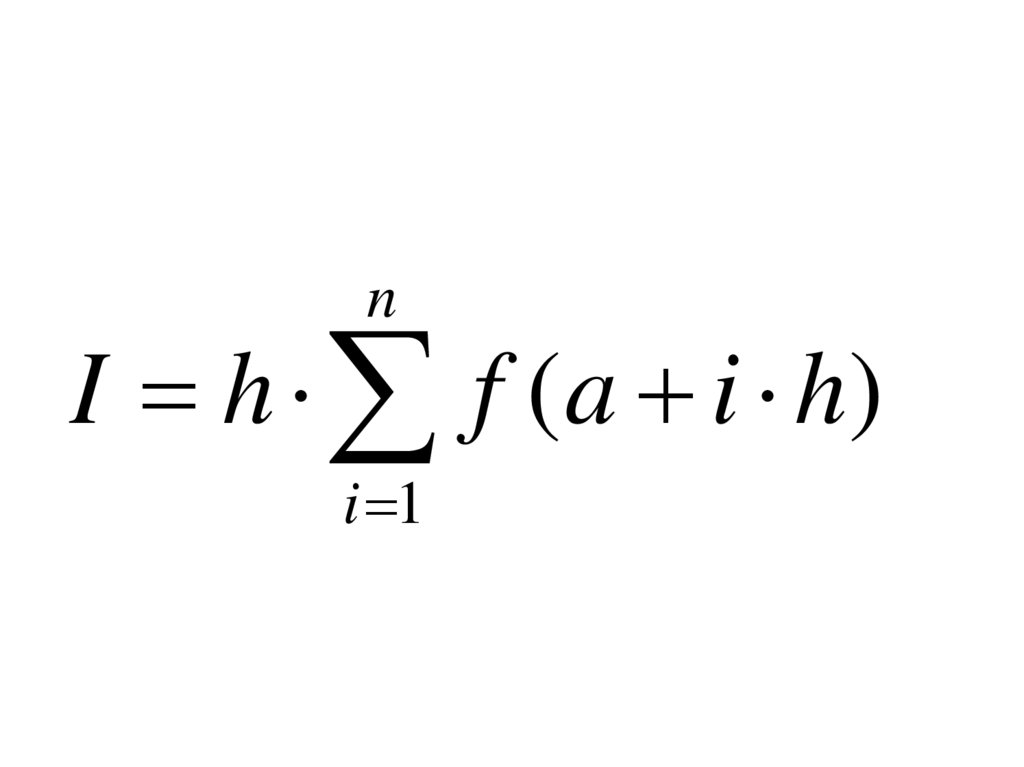


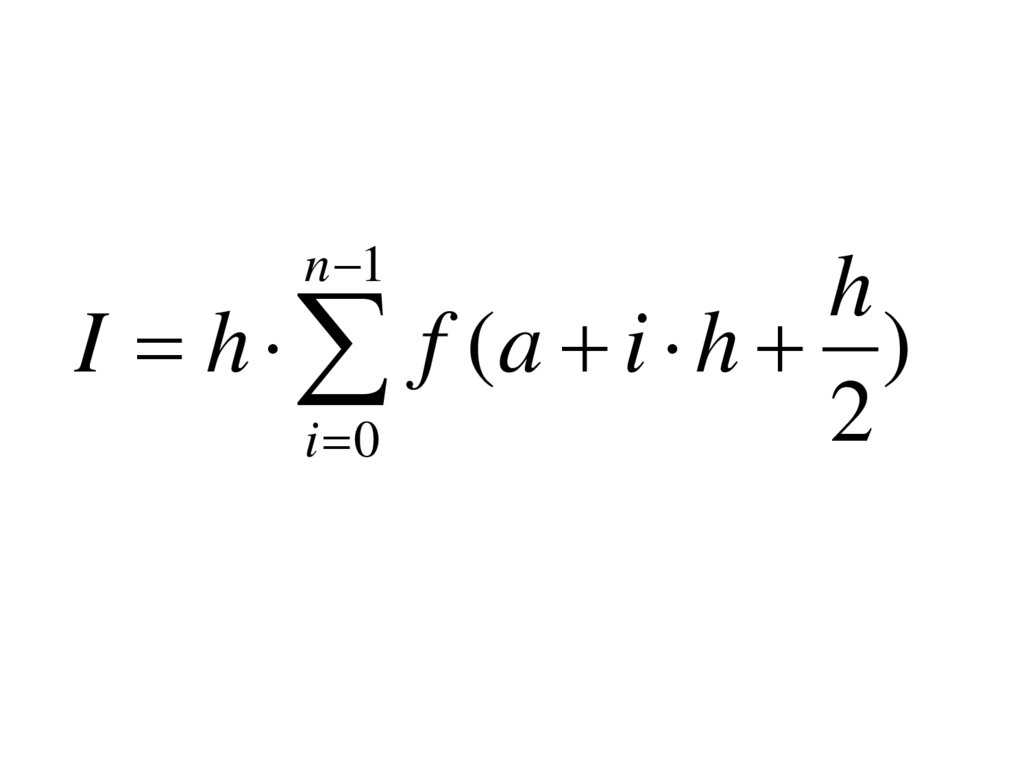








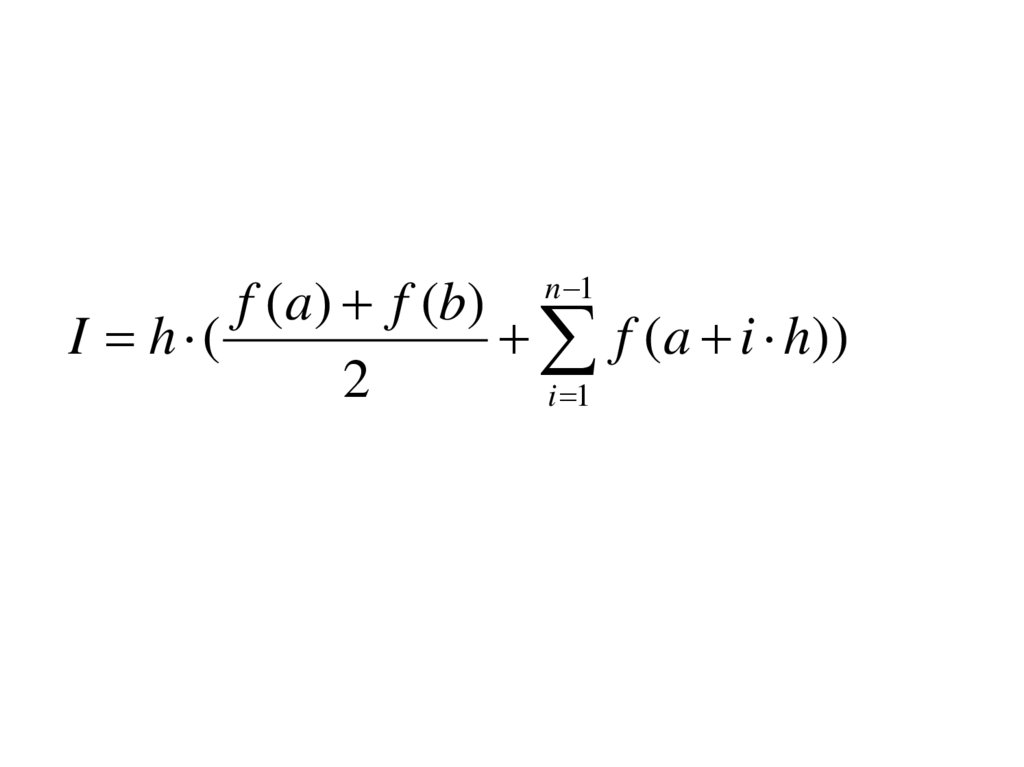


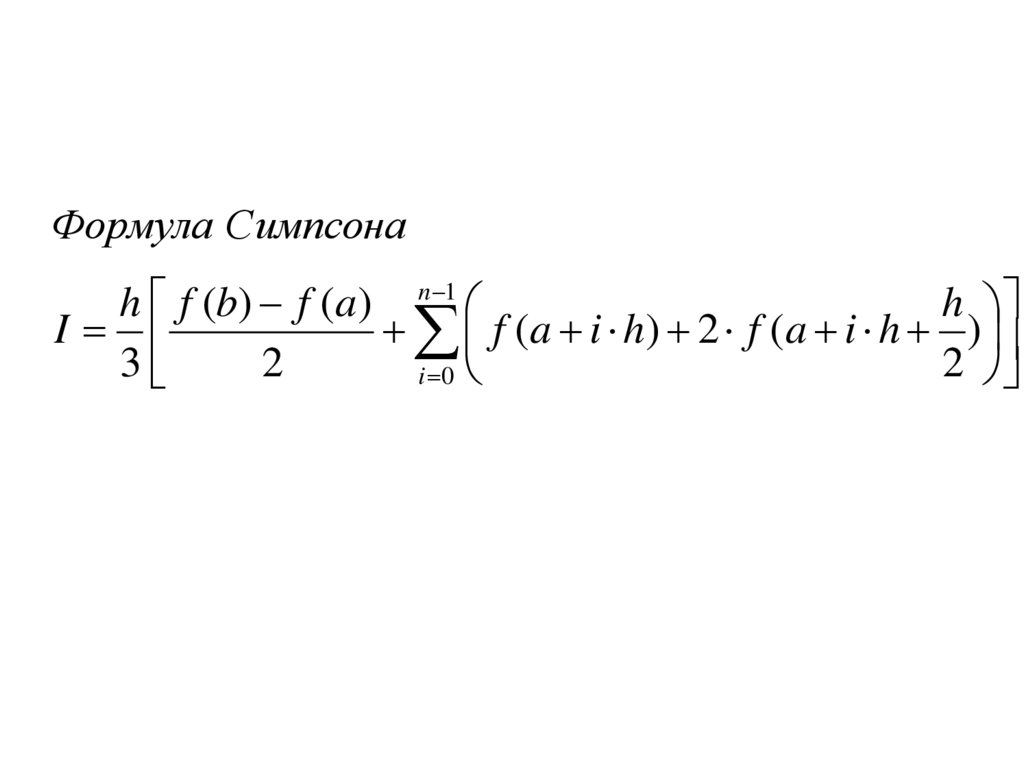


 Математика
Математика








