Похожие презентации:
Законы столкновения тел
1.
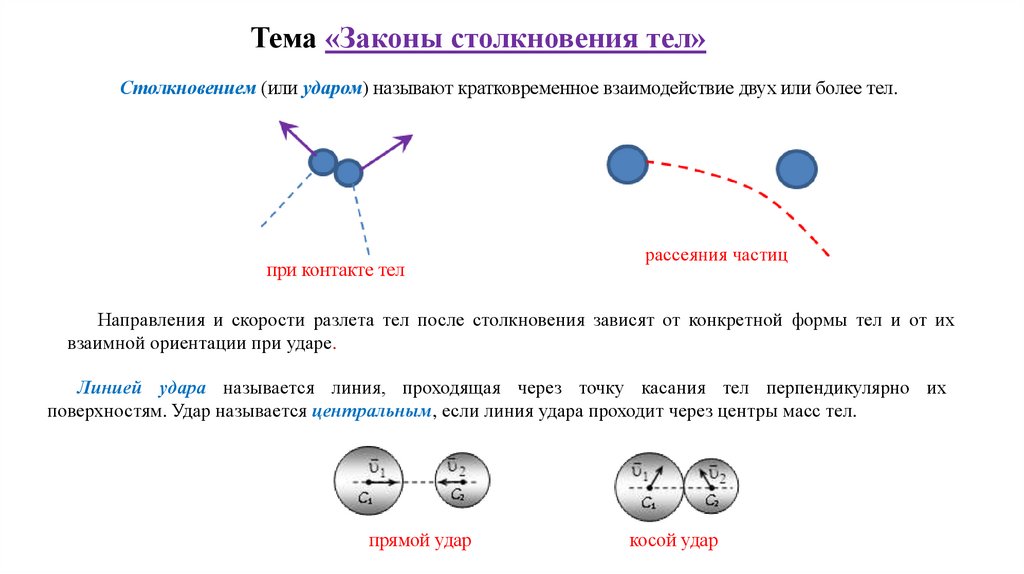
Тема «Законы столкновения тел»Столкновением (или ударом) называют кратковременное взаимодействие двух или более тел.
при контакте тел
рассеяния частиц
Направления и скорости разлета тел после столкновения зависят от конкретной формы тел и от их
взаимной ориентации при ударе.
Линией удара называется линия, проходящая через точку касания тел перпендикулярно их
поверхностям. Удар называется центральным, если линия удара проходит через центры масс тел.
прямой удар
косой удар
2.
Законы сохранения при столкновении тел1) Закон сохранения импульса
p p1 p2 m1 1 m2 2 const
2) Закон сохранения энергии (следует учитывать, что кинетическая энергия сталкивающихся тел может
переходить во внутреннюю энергию, сталкивающихся тел (энергию атомов и молекул из которых состоят
тела).
Три типа столкновения тел:
1) абсолютно упругое столкновение
2) абсолютно неупругое
3) промежуточный случай – неупругое
3.
1) Абсолютно упругое столкновение– это столкновение тел, при котором их внутренняя энергия неизменяется (форма, размеры и температура тел не изменяются).
m1 12 m2 22 m1u12 m2u22
2
2
2
2
m1 1 m2 2 m1u1 m2u2
закон
энергии
сохранения
закон сохранения импульса
скорости тел до соударения
u1
скорости тел после соударения
u2
кинетической
Из закона сохранения кинетической энергии
m1 ( 12 u12 ) m2 (u22 22 )
m1 ( u1 )( 1 u1 ) m2 (u2 )(u2 )
Из закона сохранения импульса
m1 ( 1 u1 ) m2 (u2 2 )
Сохранения относительной скорости тел
1 u1 u2 2
1 2 u2 u1
отн 1 2
отн uотн
uотн u1 u2
4.
2) Абсолютно неупругое столкновение – это такое столкновение, в результате которого оба тела«слипаются» и далее движутся как единое целое.
m1 1 m2 2 (m1 m2 )u
закон сохранения импульса
Относительные скорости тел
отн 1 2 0
относительная скорость до соударения
uотн u1 u2 0
относительная скорость после соударения
3) Неупругое столкновение – это такое столкновение, в результате которого внутренняя энергия
разлетающихся после столкновения тел изменяется, а следовательно, изменяется и суммарная кинетическая
энергия системы.
отн | 0
| uотн | 0
| uотн | отн |
из-за потерь энергии
5.
Коэффициент восстановления скорости kc:kc
| uотн | | u1 u2 |
отн | 1 2 |
kc = 1 для абсолютно упругих столкновений
kc = 0 для абсолютно неупругих столкновений
0 < kc < 1 для неупругих столкновений
Коэффициент восстановления кинетической энергии kэ:
K
kэ
K
K
m1 12
2
m2 22
2
kэ = 1 для абсолютно упругих столкновений
kэ < 1 для неупругих столкновений
m1u12 m2u22
K
2
2
6.
Механические колебания и волны7.
Тема «Гармонические колебания и их характеристики»Колебанием, или колебательным движением, в физике называют всякий периодический, т. е.
повторяемый с течением времени, или почти периодический процесс, в котором какая-либо физическая
величина принимает одинаковые значения через равные промежутки времени.
Систему способную совершать колебательные движения называют осциллятором.
Свободными, или собственными колебаниями называют колебания совершающиеся за счет
первоначально сообщенной энергии без внешних воздействий.
Гармонические колебания происходящие по закону косинуса или синуса
x A cos( t ) A sin( t 1 )
x – смещение тела от положения равновесия;
А – амплитуда колебаний (максимальное отклонение тела от положения равновесия);
– фаза колебаний;
t ( 1 t 1 )
– угловая, или циклическая частота колебаний;
( 1) –начальная фаза колебаний (фаза колебаний в момент времени t=0)
1 2
8.
Период колебаний T – это время одного полного колебания2
T
[T ] c
Частота колебаний это число колебаний в единицу времени
1
T 2
1
[ ] Гц
c
Скорость гармонически колеблющегося тела
dx
x
x
dt
x A cos( t )
x A sin( t ) A cos( t )
2
Скорость изменяется по гармоническому закону с амплитудой
A A
9.
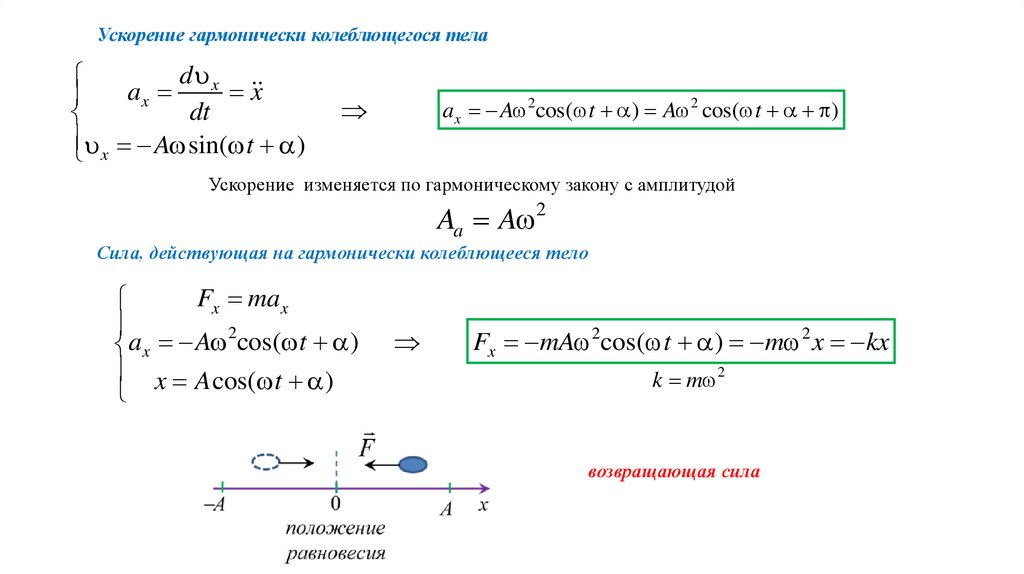
Ускорение гармонически колеблющегося телаd x
ax
x
dt
x A sin( t )
ax A 2cos( t ) A 2 cos( t )
Ускорение изменяется по гармоническому закону с амплитудой
Aa A 2
Сила, действующая на гармонически колеблющееся тело
Fx max
2
a
A
cos( t )
x
x A cos( t )
Fx mA 2cos( t ) m 2 x kx
k m 2
возвращающая сила
10.
Дифференциальное уравнение, описывающее гармонические колебанияFx max kx
d 2x
ax 2 x
dt
2
k
m
x x 0
2
Его решение
x A cos( t ),
k
m
Справедливо для малых отклонений величины от положения равновесия.
11.
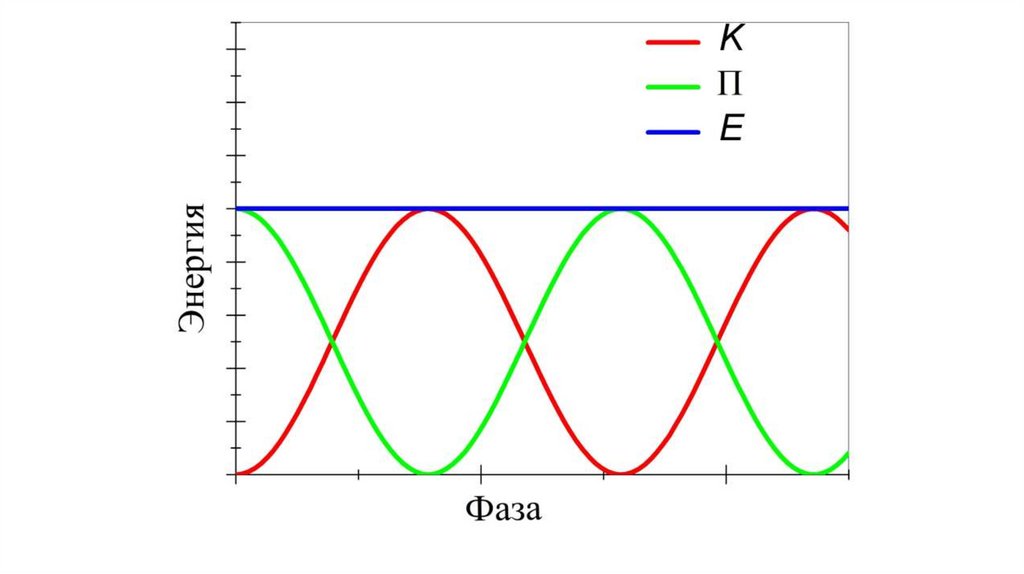
Тема «Энергия при гармонических колебаниях»Кинетическая энергия тела, совершающего гармонические колебания
m 2
K
2
A sin( t )
x
mA2 2 2
mA2 2
K
sin ( t )
(1 cos 2( t ))
2
4
периодическя фукция, изменяющаяся с частотой 2
Потенциальная энергия тела, совершающего гармонические колебания
Fx kx, k m 2
kx 2
П
2
x A cos( t )
kA2
mA2 2
2
П
cos ( t )
(1 cos 2( t ))
2
4
периодическя фукция, изменяющаяся с частотой 2
Полная механическая энергия тела, совершающего гармонические колебания
mA2 2
E K П
const
2
Является следствием консервативности
возвращающей силы
12.
13.
Тема «Простые колебательные»1. Физический маятник.
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг
неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела.
Вращательный момент силы тяжести
M z mgl sin
Угловое ускорение
d d 2
2
dt
dt
Основной закон динамики вращательного движения
Основной закон динамики вращательного движения
I z M z
I z mgl sin
Iz момент инерции
Рассмотрим малые колебания
sin
14.
Дифференциальное уравнение, описывающее колебания маятникаI z mgl
0
2
Дифференциальное уравнение армонических колебаний
Решение
0 cos( t ),
Период колебаний физического маятника
T
2
Iz
2
mgl
mgl
Iz
15.
2. Математический маятникМатематический маятник – это идеализированная система, состоящая из материальной точки
массой m, подвешенной на невесомой и нерастяжимой нити и колеблющейся под действием силы тяжести.
Момент инерции маятника
I z ml 2
Циклическая частота колебаний маятника
mgl
Iz
g
l
Период колебаний математического маятника
2
l
T
2
g
16.
2. Пружинный маятникПружинный маятник - это материальная точка массой m, подвешенная (или расположенная
горизонтально) на пружине жесткостью k и совершающая колебания под действием силы упругости.
Fx kx
Ускорение тела
d d 2x
ax
2 x
dt dt
Fупр
Закон динамики (второй закон Ньютона)
max Fx
mx kx
Дифференциальное уравнение, описывающее колебания маятника
x x 0,
2
Решение
k
m
x A cos( t )
Период колебаний пружинного маятника
2
m
T
2
k
0
l = x
x
x
17.
Тема «Сложение гармонических колебаний»1. Сложение колебаний одинакового направления (метод векторных диаграмм)
Даны два гармонических колебания, происходящих вдоль одного направления, с одинаковой
частотой
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
Требуется найти суммарное колебание
x x1 x2
Метод векторных диаграмм
Гармоническому колебанию ставится в соответствие вектор
x A cos( t )
A =A
A
18.
x1 A1 cos( t 1 )A1
x2 A2 cos( t 2 )
A2
x x1 x2
A A1 A2
x x1 x2 A cos( t )
A A1 A2 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2cos 2
19.
2. Сложение взаимно перпендикулярных колебанийРассмотрим сложение двух гармонических колебаний одинаковой частоты , происходящих во
взаимно перпендикулярных направлениях вдоль осей x и y
x A cos t
Из уравнения (1)
Из уравнения (2)
(1)
y B cos( t )
(2)
x
x2
cos t
sin t 1 2
A
A
y
cos( t ) cos t cos sin t sin
B
y x
cos
B A
x2
y x
1 2 sin
cos
B A
A
2
y
x
x2 2
cos 1 2 sin
A
B A
y 2 2 xy
x2
2
cos
sin
B 2 AB
A2
x2
1 2 sin
A
Уравнение траектории
парабола
20.
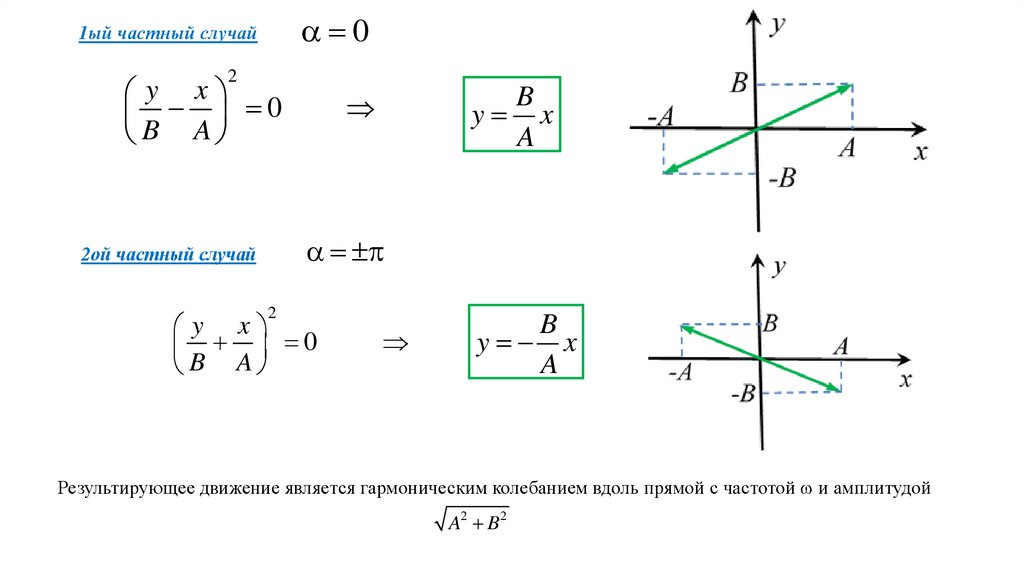
01ый частный случай
2
y x
0
B A
B
y x
A
2ой частный случай
2
y x
0
B A
B
y x
A
Результирующее движение является гармоническим колебанием вдоль прямой с частотой и амплитудой
A2 B2
21.
3ий частный случай2
y 2 x2
2 1
2
B
A

















 Физика
Физика