Похожие презентации:
Вычислительные методы и приемы математического моделирования. Практическое занятие 2
1.
Моделирование систем ипроцессов
Тема 3. Вычислительные методы и
приемы математического
моделирования
Практическое занятие 2
2.
Интерполяционная формула Лагранжаf (x)
( x x 0 )( x x 2 )...(x x n )
( x x1 )( x x 2 )...(x x n )
f (x 0 )
f ( x1 )
( x 0 x1 )( x 0 x 2 )...(x 0 x n )
( x1 x 0 )( x1 x 2 )...(x1 x n )
n
(x x k )
k 0
n
( x x 0 )( x x1 )...(x x n 1 )
k i
...
f (x n )
n
( x n x1 )( x n x 2 )...(x n x n 1 )
i 0
f (x i )
(x i x k )
k 0
k i
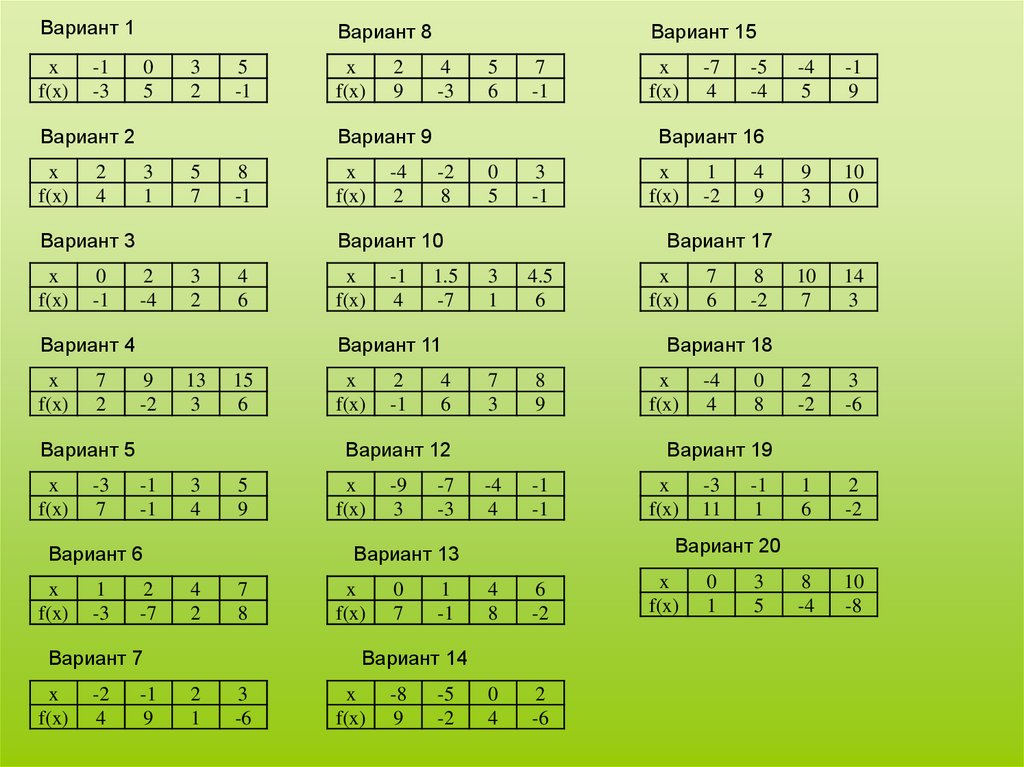
Пример. Построить интерполяционный многочлен Лагранжа для функции,
заданной таблично:
X
-0.5
0
1
f(x)
-0.21
-1.50
0.53
( x 0)( x 1)
( x 0.5)( x 1)
( 0.21)
( 1.50)
( 0.5 0)( 0.5 1)
(0 0.5)(0 1)
( x 0.5)( x 0)
0.53 3.07x 2 1.04x 1.50
(1 0.5)(1 0)
Pn ( x )
3.
Вариант 1x
f(x)
Вариант 8
-1
-3
0
5
3
2
5
-1
Вариант 2
x
f(x)
2
4
0
-1
3
1
5
7
8
-1
7
2
2
-4
3
2
4
6
-3
7
9
-2
13
3
15
6
1
-3
-1
-1
3
4
5
9
-2
4
x
f(x)
-4
2
x
f(x)
-1
4
x
f(x)
2
-1
2
-7
-1
9
x
f(x)
-9
3
4
2
7
8
x
f(x)
0
7
-2
8
0
5
3
-1
3
-6
x
f(x)
-8
9
-7
4
-5
-4
-4
5
-1
9
1.5
-7
4
6
-7
-3
1
-1
-5
-2
x
f(x)
1
-2
4
9
9
3
10
0
10
7
14
3
2
-2
3
-6
1
6
2
-2
8
-4
10
-8
Вариант 17
3
1
4.5
6
x
f(x)
7
6
8
-2
Вариант 18
7
3
8
9
x
f(x)
-4
4
0
8
Вариант 19
-4
4
-1
-1
x
f(x)
-3
11
-1
1
Вариант 20
4
8
6
-2
0
4
2
-6
Вариант 14
2
1
x
f(x)
Вариант 16
Вариант 13
Вариант 7
x
f(x)
7
-1
Вариант 12
Вариант 6
x
f(x)
5
6
Вариант 11
Вариант 5
x
f(x)
4
-3
Вариант 10
Вариант 4
x
f(x)
2
9
Вариант 9
Вариант 3
x
f(x)
x
f(x)
Вариант 15
x
f(x)
0
1
3
5
4.
Интерполяционная формула НьютонаКонечные разности
Пусть известны значения некоторой функции y=f(x) для
равноотстоящих значений аргумента
x k x 0 kh, ( k 0, n)
y0 f ( x 0 )
y1 f ( x1 )
yn f (x n )
Конечными разностями первого порядка называются величины
y1 y2 y1
y0 y1 y0
yk yk 1 yk
второго порядка:
y0 y1 y0
2
y1 y2 y1
2
2 y k y k 1 y k и т.д.
Конечные разности (m+1) порядка
m 1y0 m y1 m y0
m 1y1 m y2 m y1
m 1yk m yk 1 m yk
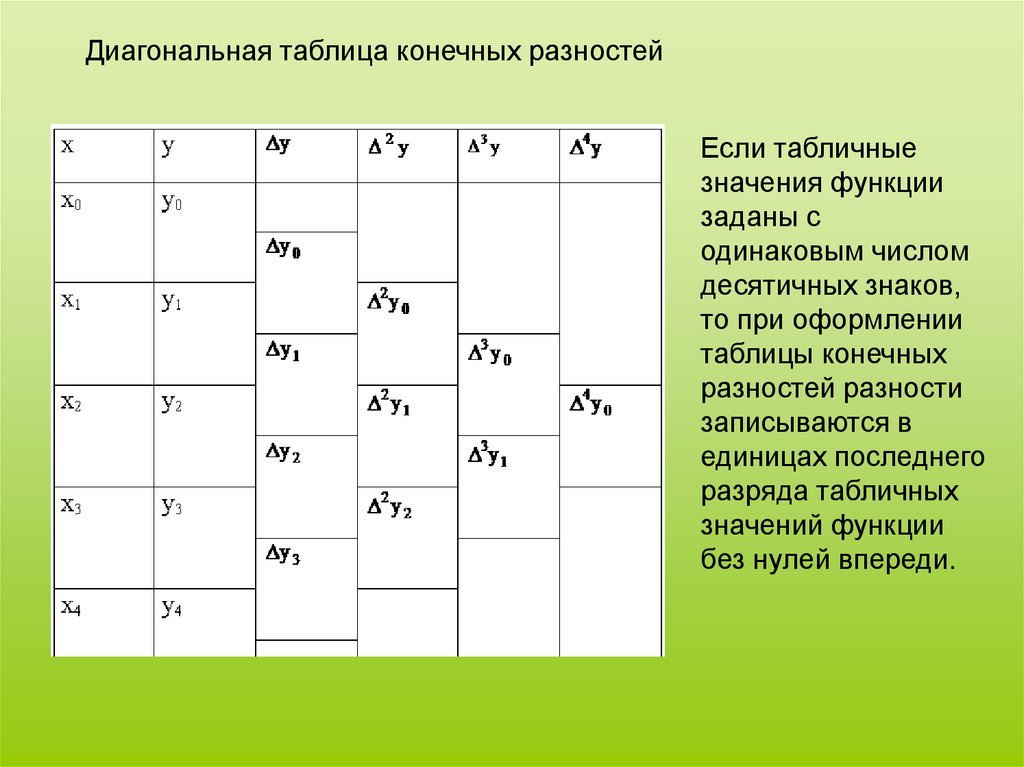
5.
Диагональная таблица конечных разностейЕсли табличные
значения функции
заданы с
одинаковым числом
десятичных знаков,
то при оформлении
таблицы конечных
разностей разности
записываются в
единицах последнего
разряда табличных
значений функции
без нулей впереди.
6.
Ищем интерполяционный многочлен в видеPn ( x ) a0 a1( x x0 ) a2 ( x x0 )( x x1 ) ... an ( x x0 )( x x1 )...( x xn 1 )
Первая интерполяционная формула Ньютона
y0
2 y0
n y0
Pn ( x ) y0
( x1 x0 )
( x x0 )( x x1 ) ...
( x x0 )( x x1 )...( x xn 1 )
2
n
h
2! h
n! h
q
x x0
h
Pn ( x ) Pn ( x0 hq ) y0 q y0
q( q 1 ) 2
q( q 1 )...q( q n 1 ) n
y0 ...
y0
2!
n!
Пусть точка интерполирования х лежит вблизи конечной точки хn или справа от нее.
Для уменьшения погрешности узлы интерполяции следует использовать в порядке
хn, xn-1, …, x0.
Pn ( x ) a0 a1( x xn ) a2 ( x xn )( x xn 1 ) ... an ( x xn )( x xn 1 )...( x x1 )
Вторая интерполяционная формула Ньютона
yn 1
2 yn 2
n y0
Pn ( x) yn
( x xn )
( x xn )( x xn 1 ) ...
( x xn )...( x x1 )
h
2!h 2
n!h n
Pn ( x ) Pn ( xn hq ) yn q yn 1
q( q 1 ) 2
q( q 1 )...q( q n 1 ) n
yn 2 ...
y0
2!
n!
7.
Пусть точка интерполирования х лежит вблизи конечной точки хn или справа от нее.Для уменьшения погрешности узлы интерполяции следует использовать в порядке хn, xn-1,
…, x0.
Pn ( x ) a0 a1( x xn ) a2 ( x xn )( x xn 1 ) ... an ( x xn )( x xn 1 )...( x x1 )
x xn
Pn ( x n ) a 0 y n
x x n 1
Pn ( x n 1 ) a 0 a1 ( x n 1 x n ) y n 1
x x n 2
y n y n 1 y n 1
a1
y n 1 y n a1h
h
h
Pn ( x n 2 ) a 0 a1 ( x n 2 x n ) a 2 ( x n 2 x n )( x n 2 x n 1 ) y n 2
y n y n 1
yn 2 yn
( 2h ) a 2 ( 2h )( h )
h
k y n k
ak
, ( k 1, n)
k
k! h
y n 2y n 1 y n 2 2 y n 2
a2
2
2! h
2! h 2
Вторая интерполяционная формула Ньютона
yn 1
2 yn 2
n y0
Pn ( x ) yn
( x xn )
( x xn )( x xn 1 ) ...
( x xn )...( x x1 )
2
n
h
2! h
n! y
Pn ( x ) Pn ( xn hq ) yn q yn 1
q( q 1 ) 2
q( q 1 )...q( q n 1 ) n
yn 2 ...
y0
2!
n!
8.
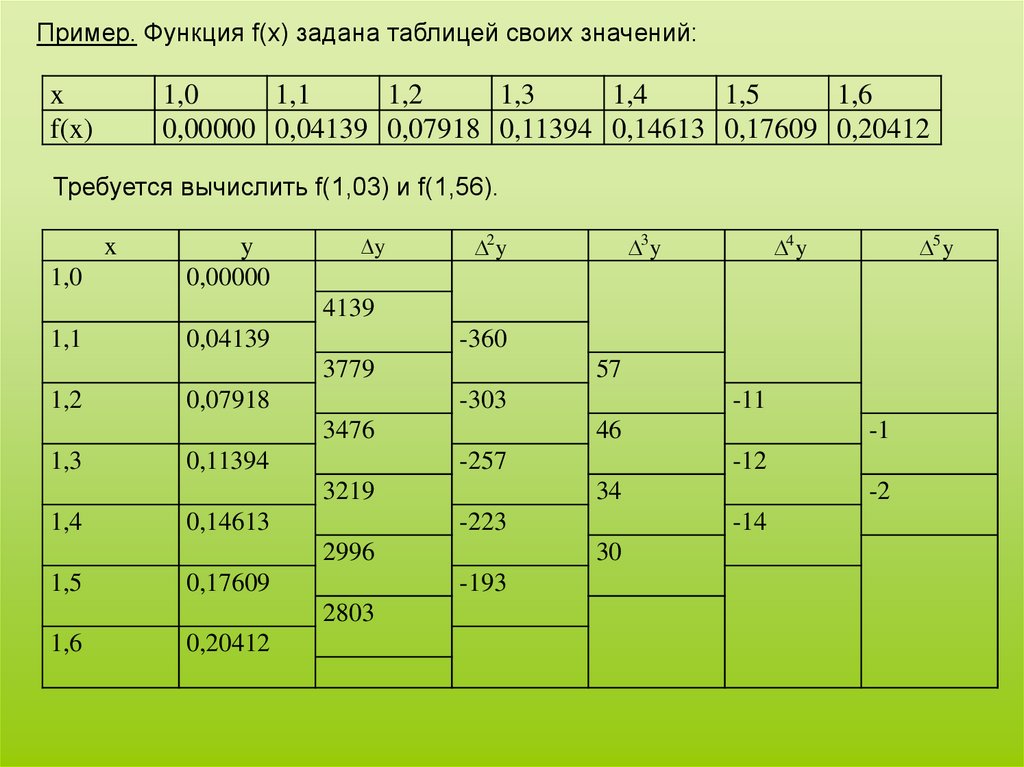
Пример. Функция f(x) задана таблицей своих значений:x
f(x)
1,0
1,1
1,2
1,3
1,4
1,5
1,6
0,00000 0,04139 0,07918 0,11394 0,14613 0,17609 0,20412
Требуется вычислить f(1,03) и f(1,56).
x
1,0
y
0,00000
y
2 y
4 y
3 y
5 y
4139
1,1
0,04139
-360
3779
1,2
0,07918
57
-303
3476
1,3
0,11394
46
-257
3219
1,4
0,14613
0,20412
-2
-14
30
-193
2803
1,6
-12
-223
0,17609
-1
34
2996
1,5
-11
9.
x0=1,0; h=0,1; m=4x x 0 1,03 1,0
q
0,3
h
0,1
Pn ( x ) Pn ( x0 hq ) y0 q y0
q( q 1 ) 2
q( q 1 )...q( q n 1 ) n
y0 ...
y0
2!
n!
q(q 1) 2
q(q 1)( q 2) 3
P4 (1,03) y0 q y0
y0
y0
2!
3!
q(q 1)( q 2)( q 3) 4
y0 0,00000 0,3 0,04139
4!
0,3( 0,7)
0,3( 0,7)( 1,7)
( 0,00360)
0,00057
2
6
0,3( 0,7)( 1,7)( 2,7)
( 0,00011) 0,012833
24
10.
xn=1,6; h=0,1; m=4x x n 1,56 1,6
q
0,4
h
0,1
q(q 1) 2
q(q 1)(q 2) 3
P4 (1,56) y n q y n 1
yn 2
y n 3
2!
3!
q(q 1)(q 2)(q 3) 4
y n 4 0,20412 0,4 0,02803
4!
( 0,4)( 0,6)
( 0,4)(0,6)(1,6)
( 0,00193)
0,00030
2
6
( 0,4)( 0,6)(1,6)( 2,6)
( 0,00014) 0,193127
24







 Математика
Математика








