Похожие презентации:
Вероятностно-статистические основы эконометрики
1. Вероятностно-статистические основы эконометрики
2.
Вероятностный эксперимент (испытание) — эксперимент, результаткоторого не предсказуем заранее, так как он является случайным в силу
сложного сочетания естественных причин.
Любое действие в экономике по своей сути является вероятностным
экспериментом. Например, строительство автомобильного завода в контексте
получения прибыли является вероятностным экспериментом.
Событие — это любой исход или совокупность исходов какого-либо
вероятностного эксперимента. Получение прибыли можно рассматривать как
результат строительства завода.
Событие, которое может произойти или не произойти в условиях данного
эксперимента, называется случайным (прибыль может быть, а может и не
быть).
Если событие происходит всегда в условиях данного эксперимента, то оно
называется достоверным (спрос на автомобили упадет при резком снижении
доходов населения).
Событие называется невозможным, если оно не происходит никогда в
условиях данного эксперимента (при прочих равных условиях рост спроса на
автомобили приводит к снижению их цены).
28.02.2010
Р. Мунипов
2
3.
События, которые не могут происходить одновременно, называютсянесовместимыми (увеличение налогов — рост располагаемого дохода). В
противном случае они называются совместимыми (увеличение объема продаж
— увеличение прибыли).
Два события называются противоположными, если одно из них происходит
тогда и только тогда, когда не происходит другое (товар реализован — товар не
реализован).
Событие, которое нельзя разбить на более простые, называется элементарным
(продажа автомобиля).
Событие, представимое в виде совокупности (суммы) нескольких
элементарных событий, называется составным (предприятие не потерпело
убытки — прибыль может быть положительной либо равной нулю).
Вероятность события — это количественная мера, которая вводится для
сравнения событий по степени возможности их появления.
28.02.2010
Р. Мунипов
3
4.
Классическое определение вероятности.Вероятностью события A , обозначается P( A) , называется отношение m
числа элементарных событий (исходов), благоприятствующих появлению
события A , к числу n всех элементарных событий в условиях данного
вероятностного эксперимента:
m
P( A)
n
Из определения вытекают следующие свойства вероятности:
1. Значение вероятности события находится в пределах от нуля до единицы
0 P( A) 1
2.
3.
4.
5.
Вероятность достоверного события равна 1: .
Вероятность невозможного события равна 0: .
Если события A и B несовместимы, то P( A B) P( A) P( B)
Если A и A есть противоположные события, то P( A) 1 P( A)
При статистическом определении вероятности события A под n понимается
количество наблюдений результатов эксперимента, в которых событие А
встретилось ровно m раз. В этом случае отношение называется
относительной частотой события A.
28.02.2010
Р. Мунипов
4
5.
События, которые не могут происходить одновременно, называютсянесовместимыми (увеличение налогов — рост располагаемого дохода). В
противном случае они называются совместимыми (увеличение объема продаж
— увеличение прибыли).
Два события называются противоположными, если одно из них происходит
тогда и только тогда, когда не происходит другое (товар реализован — товар не
реализован).
Событие, которое нельзя разбить на более простые, называется элементарным
(продажа автомобиля).
Событие, представимое в виде совокупности (суммы) нескольких
элементарных событий, называется составным (предприятие не потерпело
убытки — прибыль может быть положительной либо равной нулю).
Вероятность события — это количественная мера, которая вводится для
сравнения событий по степени возможности их появления.
При статистическом определении вероятности события А под n понимается
количество наблюдений результатов эксперимента, в которых событие А
встретилось ровно т раз. В этом случае отношение называется относительной
частотой события А.
28.02.2010
Р. Мунипов
5
6.
Случайной величиной (СВ) называют величину, которая в результатенаблюдения принимает то или иное значение, заранее не известное и
зависящее от случайных обстоятельств. Например, объем ВНП, количество
реализованной продукции, прибыль фирмы, размер чистого экспорта за год и
т.д. являются случайными величинами.
Различают дискретные и непрерывные СВ.
Дискретной называют такую СВ, которая принимает отдельные,
изолированные значения с определенными вероятностями (такая СВ имеет
счетное количество значений). Например, можно считать, что число
покупателей в магазине, побывавших там в течение дня, число автомобилей,
ремонтируемых еженедельно в данной мастерской, число находящихся в
аэропорту самолетов являются дискретными СВ.
Однако большинство СВ, рассматриваемых в экономике, имеют настолько
большое число возможных значений, что их удобнее представлять в виде
непрерывных СВ.
Непрерывной называют такую СВ, которая может принимать любое значение
из некоторого конечного или бесконечного числового промежутка (т.е.
количество возможных значений непрерывной СВ не счетно). Например,
курсы валют, доход, объемы ВНП, ВВП и т.п. обычно рассматриваются как
непрерывные СВ.
28.02.2010
Р. Мунипов
6
7.
Соответствие между всеми возможными значениями СВ и их вероятностями.называется законом распределения дискретной СВ, или функцией
распределения.
Табличное задание закона распределения дискретной СВ принимающей
значения x1 , x2 , xn с вероятностями p1 , p2 , pn соответственно имеет вид:
X
pi
причем, x1 x2
28.02.2010
x1
p1
x2
p2
xn
pn
xn , p1 p2
pn 1
Р. Мунипов
7
8.
Пример На станции технического обслуживания, на основании данных,полученных по 100 автомобилям, выяснилось, что для 25 из них требуется 1 ч
для проведения профилактических работ. Мелкий ремонт требуется для 40
автомобилей, что занимает 2 ч. Для 20 автомобилей требуется ремонт с
заменой отдельных узлов, что занимает в среднем 5 ч. 10 автомобилей могут
быть отремонтированы за 10 ч. Для 5 автомобилей необходимое время
ремонта составляет 20 ч. Построить закон распределения СВ X — времени
обслуживания случайно выбранного автомобиля.
X
pi
28.02.2010
1
2
5
10
20
0,25
0,40
0,20
0,10
0,05
Р. Мунипов
8
9.
Функцией распределения СВ X называют функцию F ( x) , определяющуювероятность того, что СВ X принимает значение меньшее, чем x , т.е.
F ( x ) P( X x )
Иногда эту функцию называют функцией накопленной вероятности или
кумулятивной функцией распределения.
Из определения вытекают свойства функции распределения:
1. 0 F ( x) 1
2. x1 x2 F ( x1 ) F ( x2 )
3.
lim F ( x) 0, lim F ( x) 1
x
x
4. P(a X b) F (b) F (a )
5. P( X x) 1 F ( x)
0, x a,
6. X a, b F ( x)
1, x b
28.02.2010
Р. Мунипов
9
10.
Xpi
1
2
5
10
20
0,25
0,40
0,20
0,10
0,05
x 1
0
0,25 1 x 2
0,65 2 x 5,
F(X )
0,85 5 x 10,
0,95 10 x 20,
x 20
1
1,00
0,95
0,85
Функция распределения
дискретной СВ имеет
ступенчато образный
график
0,65
0,25
1 2
28.02.2010
5
10
20
Р. Мунипов
10
11.
Плотностью вероятности (плотностью распределения вероятностей)непрерывной СВ X называют функцию:
f ( x)
или:
P( x X x x)
x
F ( x x) F ( x)
f ( x) lim
F ( x)
x 0
x
плотность вероятности равна производной от функции распределения
(поэтому иногда её называют дифференциальной функцией распределения).
Свойства функции плотности распределения СВ:
1. f ( x) 0
b
2. P (a X b) f ( x)dx
a
x
3. F ( x)
f (t )dt
4.
f ( x)dx 1
Условие
нормировки
28.02.2010
Р. Мунипов
11
12.
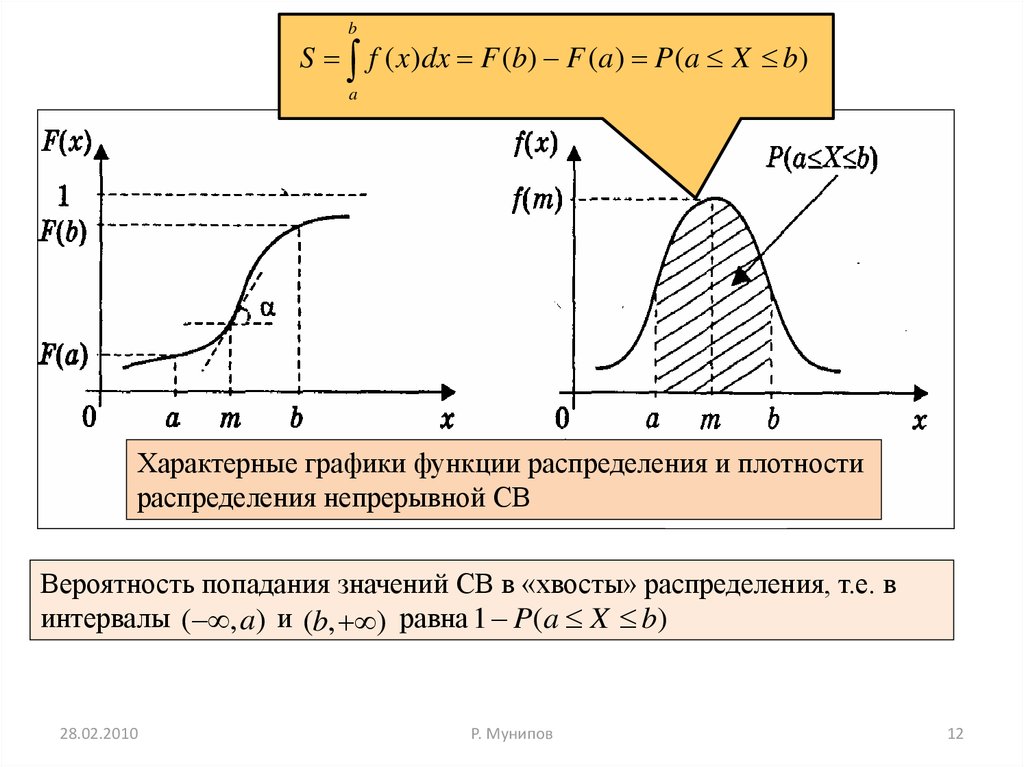
bS f ( x)dx F (b) F (a ) P(a X b)
a
Характерные графики функции распределения и плотности
распределения непрерывной СВ
Вероятность попадания значений СВ в «хвосты» распределения, т.е. в
интервалы ( , a) и (b, ) равна 1 P(a X b)
28.02.2010
Р. Мунипов
12
13.
Математическое ожидание M ( X ) определяетсядля дискретной СВ:
M ( X ) x1 p1 x2 p2
k
xk pk xi pi
i 1
где k — число всех возможных значений СВ X ,
для непрерывной СВ:
M (X )
xf ( x)dx
Математическое
ожидание характеризует
среднее ожидаемое
значение СВ, и
приближенно равно её
среднему значению.
Свойства математического ожидания:
1. M ( ) , где
константа.
2. M ( X ) M ( X ) .
3. M ( X Y ) M ( X ) M (Y ) .
4. M (aX b) aM ( X ) b , где a и b константы.
5. M ( XY ) M ( X ) M (Y ) , где X и Y независимые СВ.
X
pi
1
2
5
10
20
0,25
0,40
0,20
0,10
0,05
M ( X ) 1 0,25 2 0,40 5 0,20 10 0,10 20 0,05 4,05
28.02.2010
Р. Мунипов
13
14.
Дисперсией D( X ) СВ называется математическое ожидание квадратаотклонения СВ от ее математического ожидания,
Дисперсия
2
2
2
D( X ) M X M ( X ) M ( X ) M ( X )
характеризует разброс
возможных значений
для дискретной СВ:
k
k
СВ относительно её
2
2
2
D( X ) xi M ( X ) pi xi pi M ( X )
среднего значения
i 1
i 1
(математического
где k — число всех возможных значений СВ,
ожидания).
для непрерывной СВ:
D( X )
x M ( X )
2
f ( x)dx
x 2 f ( x)dx M ( X )
2
Свойства дисперсии:
1. D( ) 0 , где константа.
2. D( X ) 2 D( X ) .
3. D( X Y ) D( X ) D(Y ) .
4. D(aX b) a 2 D( X ), где a и b константы.
Средним квадратическим отклонением ( X ) СВ называют квадратный
корень из дисперсии: ( X ) D( X )
28.02.2010
Р. Мунипов
14
15.
Xpi
1
2
5
10
20
0,25
0,40
0,20
0,10
0,05
M ( X ) 4,05
D( X ) 1 4,05 0,25
2
2 4,05 0,40
2
5 4,05 0,20
2
10
4,05
0,10
2
20
4,05
0,05 20,4475
2
( X ) 20,4475 4,522
28.02.2010
Р. Мунипов
15
16.
Нормальное распределениеСВ X имеет нормальное распределение, если ее плотность вероятности
имеет вид:
1
f x
e
2
Функция распределения F x
( x m )2
2 2
1
2
.
x
e
t m 2
2 2
dt.
M ( X ) m , дисперсия D( X ) 2
При
этом математическое ожиданиеР. Мунипов
28.02.2010
16
17.
Если СВ X имеет нормальное распределение с параметрамиматематического ожидания M ( X ) m и дисперсией D( X ) 2
то X
N (m, 2 )
СВ X
N (0,1) называется стандартизированной
СВ X
N (0,1) обозначим через U , т.е. U
1
f u
e
2
Если СВ X
u2
2
1
F u
2
;
N (m, 2 ) то U
Функция Лапласа: u
Вероятность того, что CВ X
исчисляется
N (0,1)
X m
1
2
u
e
t2
2
u
e
t2
2
dt.
N (0,1)
dt F u 0,5.
0
N (m, 2 ) будет принимать значения между a и b
b m
a m
b m
a m
P a X b F
F
.
28.02.2010
Р. Мунипов
17
18.
Закон3
(трех сигм)
Справедливо X
P X m 0.68
2
N ( m, ) : P X m 2 0.95
P X m 3 0.9973
S 0.68
m
S2 0.95
m m
m 2
m
Площадь под кривой функции
нормального распределения
полностью (99,73%) определяется
интервалом m 3
Значения СВ X N (m, 2 ) на
99,73% сосредоточены в интервале
28.02.2010
m ; m
m 2
S3 0.9973
m 3
Р. Мунипов
m
m 18
3
19.
Линейная комбинация нормальных СВ имеет нормальное распределениеX
Y
N (mx , x2 )
Z aX bY
2
N (my , y )
mz amx bm y
N (mz , ) 2
2 2
2 2
a
b
y
z
x
2
z
Многие экономические показатели имеют нормальный или близкий к
нормальному закон распределения. Например, доход населения, прибыль
фирм в отрасли, объем потребления и т.д. имеют близкое к нормальному
распределение.
Нормальное распределение используется при проверке различных гипотез в
статистике (о величине математического ожидания при известной дисперсии,
о равенстве математических ожиданий и т.д.).
При моделировании экономических процессов приходится рассматривать СВ,
которые представляют собой алгебраическую комбинацию нескольких СВ.
При этом желательно иметь возможность прогнозирования поведения таких
СВ.
28.02.2010
Р. Мунипов
19
20.
Распределение 2 (хи-квадрат)Пусть СВ U i N (0,1) , тогда СВ
степенями свободы,
2
U
i 1 i имеет хи-квадрат распределение с n
n
n
n U i 2 U12 U 2 2
2
i 1
U n2
Число степеней свободы v исследуемой СВ определяется количеством n СВ,
ее составляющих, уменьшенным на число линейных связей между ними.
Например, число степеней свободы СВ, являющейся композицией случайных
величин, которые в свою очередь связаны m линейными уравнениями,
определяется числом v n m
Очевидно, U 2 12
С увеличением числа степеней
свободы 2 распределение
приближается к нормальному
M 2
28.02.2010
D 2 2
Р. Мунипов
20
21.
Xn
Y
m
2
2
Z X Y
n2 m
Если СВ X n 2 и Y m 2 имеют
распределение хи-квадрат с n и m
степенями свободы, то их сумма также
имеет распределение хи-квадрат с
степенями свободы n m
Распределение хи-квадрат применяется для нахождения интервальных
оценок и проверки статистических гипотез
28.02.2010
Р. Мунипов
21
22.
Распределение СтьюдентаПусть СВ U N (0,1) , СВ V — независимая от U величина, распределённая
2
по закону с n степенями свободы. Тогда величина СВ
U
T
V n
имеет распределение Стьюдента (t-распределение) с n степенями свободы
T Tn
С увеличением числа степеней свободы n распределение Стьюдента
приближается к стандартизированному нормальному распределению, причем
14.02.2010
при
практически можно заменить
n 30 распределение Стьюдента
Р. Мунипов
22
28.02.2010
нормальным
распределением.
23.
Распределение ФишераПусть V и W — независимые СВ, распределенные по закону 2 со
степенями свободы m и n соответственно, тогда величина
V m
W n
имеет распределение Фишера со степенями свободы n, m F
F
Fm,n
С увеличением числа степеней свободы распределение Фишера приближается
к нормальному распределению. Причем
14.02.2010
28.02.2010
TnР.2 Мунипов
F1,n
23
24.
- квантилем (критической точкой уровня ) называется значение yСВ Y такое, что
P(Y y )
f ( y )dy
y
Квантили y и y1 называются симметричными. Если распределение
симметрично относительно оси ординат, то y y1
Нахождение квантиля геометрически заключается в таком выборе
значения, y при котором площадь заштрихованной криволинейной
трапеции под кривой плотности распределения была бы равна
28.02.2010
Р. Мунипов
24
25.
Многие экономические показатели определяются несколькими числами,являясь по сути многомерными СВ. Например, издержки предприятия
включают в себя фиксированную и переменную составляющие; уровень
жизни населения подразумевает использование большого числа показателей:
ВНП на душу населения, распределение доходов, наличие товаров и услуг,
продолжительность жизни и т.д.
Значения ряда экономических показателей предопределяют величины других
показателей. Поэтому одна из центральных задач эконометрического анализа
— выявить наличие и определить силу взаимосвязи между различными
экономическими показателями (фактически между СВ). Например, между
доходом и потреблением; между спросом на товар и его ценой; между уровнем
инфляции и уровнем безработицы; между ВНП и уровнем жизни. Вследствие
этого при проведении эконометрического анализа одно из главных мест
занимает исследование взаимосвязей СВ, при которых реализация одной из
СВ влияет на вероятность определенной реализации других СВ.
28.02.2010
Р. Мунипов
25
26.
Для описания совокупности n СВ (n-мерной СВ ) вводятся следующиепонятия:
совместная вероятность
PX1X 2
Xn
( x1, x2 , , xn ) P( X1 x1, X 2 x2 , , X n xn )
совместная функция распределения
F ( x1 , x2 ,
, xn ) P( X 1 x1 , X 2 x2 ,
, X n xn )
совместная плотность вероятностей
n F ( x1, x2 , , xn )
f ( x1, x2 , , xn )
x1 x2 xn
В частности, для установления зависимостей между двумя СВ рассматривают
двумерные вероятности, функции распределения и плотности вероятностей:
PX1 X 2 ( x1 , x2 ,
, xn ) P ( X 1 x1 , X 2 x2 )
F ( x1 , x2 ) P ( X 1 x1 , X 2 x2 )
28.02.2010
2 F ( x1 , x2 )
f ( x1 , x2 )
x1 x2
Р. Мунипов
26
27.
Если для означенных выше функций рассматриваются их значениями прификсированных величинах одной или нескольких СВ, то эти функции обычно
усредняются (суммируются или интегрируются) по другим переменным. В
результате получаются так называемые маргинальные (предельные)
вероятности, функции распределения и плотности вероятности, например:
P1 ( X 1 x1 )
x2
P
X1 X 2
Xn
, )
x1
28.02.2010
f X1 X 2
Xn
(t , x2 ,
, xn ) dtdx2
dxn
f1 ( x1 )
, xn )
xn
F1 ( x1 ) F ( x1 , ,
( x1 , x2 ,
f X1 X 2
Xn
( x1 , x2 ,
, xn )dx2
Р. Мунипов
dxn
Эти условия обычно
называют условиями
согласованности.
27
28.
Для n-мерных СВ могут быть определены условные вероятности. Например,вероятность того, что значения СВ X 1 X 2 X n 1 будут равны x1 , x2 , , xn 1
соответственно при условии, что X n xn , определяется по формуле
P X 1 x1 , X 2 x2 ,
, X n 1 xn 1 X n xn
P( X 1 x1 , X 2 x2 , , X n xn )
P( X 1 x1 )
Для двух СВ X и Y условной вероятностью (условной плотностью
вероятностей) СВ X при условии, что СВ Y примет значение у (Y = у),
называется величина
P( x, y)
P x y
,
P( y )
f ( x, y)
f ( x y)
f ( y)
Совместная вероятность (совместная плотность вероятности) СВ
P( x, y) P( X x,Y y ) P x y P( y ) P y x P( x),
f ( x, y) f ( x y) f ( y) f ( y x) f ( x)
28.02.2010
Р. Мунипов
28
29.
Для двух независимых СВ X и Y справедливоP ( x, y ) P ( x ) P ( y )
f ( x, y ) f ( x ) f ( y )
F ( x, y ) F ( x ) F ( y )
Совместная вероятность, совместная функция распределения, совместная
плотность вероятности не дают ясного представления о поведении каждой из
компонент рассматриваемой СВ и их взаимосвязи друг с другом. В этом
случае могут быть построены законы распределений каждой из составляющих
многомерной СВ. Причем любая из них принимает те же значения, но с
соответствующими маргинальными вероятностями, либо маргинальными
функциями распределения
28.02.2010
Р. Мунипов
29
30.
Двумерная дискретная СВ (X, Y) может быть задана в табличной форме.Y
X
pij P ( X xiy,1Y y j ), y2
...
yj
...
P ( X xi )
yn
x1 x ) p11p (i 1, m
p12),
P( X
ij
i
n
...
p1 j
...
p1n
P ( X x1 )
j 1
x2
pm 21
p22
P(Y y j ) pij ( j 1, n)
...
p2 j
...
p2n
P( X x2 )
...
...
...
xi
i 1
pi1
...
xm
...
pi 2
...
pij
...
pm1
pm 2
P(Y y j ) P(Y y1 ) P(Y y2 )
28.02.2010
...
...
...
...
pmj
P(Y y j )
Р. Мунипов
pin
...
...
pmn
P ( X xi )
...
P( X xm )
P(Y yn )
30
31.
Построение закона распределения многомерной СВ является задачейдостаточно громоздкой и в ряде случаев излишней. Информация о каждой из
составляющих СВ и о их взаимосвязи в этом случае не является очевидной.
Для анализа степени взаимосвязи СВ используют числовые характеристики:
смешанные моменты распределения, ковариацию и коэффициент корреляции.
Смешанным моментом порядка k, l называется величина
x k y l P ( x, y ) - для дискретных СВ
x y
mk ,l
x k y l f ( x, y )dxdy - для непрерывных СВ
В частности M ( X ) m1,0 , M (Y ) m0,1
Центральны моментом порядка k, l называется величина
k
l
k ,l M X M ( X ) Y M (Y )
В частности D( X ) 2,0 , D(Y ) 0,2
28.02.2010
Р. Мунипов
31
32.
Для описания связи между СВ X и Y применяют центральный моментпорядка 1,1 ( 1,1 ), который называется ковариацией СВ
xy cov( X ,Y ) M X M ( X ) Y M (Y ) M ( XY ) M ( X )M (Y )
Ковариация является абсолютной (зависящей от размерностей) мерой
взаимосвязи (co-vary — «совместное изменение») переменных
xi y j P ( xi , y j ) M ( X ) M (Y ) - для дискретных СВ
x y
xy
xyf ( x, y )dxdy M ( X ) M (Y ) - для непрерывных СВ
Свойства ковариации:
1. xy yx
2. xx D( X ) x 2
3. xy 0 если СВ независимые
4. xy x y
5. cov(aX b, cY d ) bd cov( X , Y ) где a, b, c, d константы
28.02.2010
Р. Мунипов
32
33.
Ковариация может служить индикатором наличия положительной(переменные изменяются в одном направлении) либо отрицательной
(переменные изменяются в разных направлениях) связи между СВ —
ковариация в этом случае положительна либо отрицательна. Однако
существенным недостатком ковариации является её зависимость от
размерностей рассматриваемых СВ. Поэтому при различных единицах
измерения СВ одна и та же зависимость может выражаться различными
значениями ковариации. Кроме того, ковариация не позволяет определить силу
(строгости) зависимости между рассматриваемыми СВ. Для устранения
данных недостатков вводится относительная мера взаимосвязи (безразмерная
величина) — коэффициент корреляции.
Коэффициентом корреляции СВ X и Y называют величину
xy
xy
xy
x y
D( X ) D(Y )
28.02.2010
Р. Мунипов
33
34.
Зависимость между СВ X и Y , характеризуемая коэффициентом корреляции,называется корреляцией. СВ X и Y называются некоррелированными,
если xy 0 , что равносильно равенству xy 0 . Если же xy 0 , то СВ X
и Y называют коррелированными.
Свойства коэффициента корреляции:
xx 1
2. xy yx
3. 1 xy 1
4. xy 0 если СВ независимые
5. xy 1 Y aX b т.е. между СВ X и Y существует линейная
1.
функциональная зависимость
Если X и Y независимые СВ, то X и Y — некоррелированные СВ. Обратное
утверждение неверно.
В случае, когда СВ не являются независимыми, а коррелируют друг друга,
формулы расчета дисперсии их суммы либо разности имеют вид:
D( X Y ) D( X ) D(Y ) 2cov( X ,Y )
28.02.2010
D( X Y ) D( X ) Р. Мунипов
D(Y ) 2 xy x y
34
35.
При исследовании реальных экономических процессов приходитсяобрабатывать большие объемы статистических данных по самым
разнообразным показателям, которые по своей сути являются СВ. Часто
возникает необходимость оценивания числовых значений различных
параметров, неоднократно приходится выдвигать и проверять различные
предположения, устанавливать наличие и силу зависимости между
разнообразными факторами. На практике сталкиваются с конкретными
реализациями рассматриваемых СВ. Количество таких реализаций
ограничено, что не позволяет применять напрямую теоретические методы
анализа. Поэтому в первую очередь используются методы и модели
математической статистики (в частности, выборочный метод), позволяющие
получать необходимые знания об исследуемом объекте, осуществлять
направленный анализ и делать обоснованные выводы.
Одной из центральных задач математической статистики является выявление
закономерностей в статистических данных, на базе которых можно строить
соответствующие модели и принимать обдуманные решения. Под
статистическими данными подразумеваются данные наблюдений за
значениями некоторой СВ или совокупности СВ, характеризующих изучаемый
процесс.
28.02.2010
Р. Мунипов
35
36.
Первая задача математической статистики — указать способы сбора игруппировки статистических данных, полученных в результате наблюдений
или испытаний.
Вторая задача математической статистики — разработать методы анализа
статистических данных в зависимости от целей исследования.
Элементами такого анализа являются:
1. оценки неизвестной вероятности события, неизвестной функции
распределения, неизвестных параметров известного распределения,
зависимости двух или нескольких случайных величин и т. п.;
2. проверка статистических гипотез о виде неизвестного распределения; о
величинах параметров известного распределения; о виде и силе
зависимости между рассматриваемыми случайными величинами.
Таким образом, основная задача математической статистики состоит в
создании методов сбора и обработки статистических данных для получения
научных и практических выводов.
Знание методов математической статистики и умение ими оперировать
являются необходимой предпосылкой для успешного эконометрического
анализа.
28.02.2010
Р. Мунипов
36
37.
Пусть изучается совокупность однородных объектов относительно некоторогоколичественного признака, характеризующего эти объекты. Например, доход
населения, количество покупателей в магазине в течение дня, количество
качественных товаров в исследуемой партии и т. д.
Генеральной совокупностью называется множество всех возможных значений
или реализаций исследуемой СВ X при данном реальном комплексе условий.
Выборкой (выборочной совокупностью) называют часть генеральной
совокупности, отобранную для изучения.
Число элементов рассматриваемой совокупности называется ее объемом.
Изучение всей генеральной совокупности во многих случаях либо
невозможно, либо нецелесообразно в силу больших материальных затрат,
уничтожения или порчи исследуемых объектов. Например, анализ среднего
дохода населения формально предполагает наличие достоверной информации
о каждом жителе города в конкретный момент времени. Получение такой
информации практически невозможно
28.02.2010
Р. Мунипов
37
38.
На практике вся генеральная совокупность поэлементно никогда неанализируется. Для осуществления выводов о генеральной совокупности чаще
всего используется выборка ограниченного объема. В силу этого задача
математической статистики состоит в исследовании свойств выборки и
обобщении этих свойств на генеральную совокупность. Полученный при этом
вывод называется статистическим.
Информация о генеральной совокупности, полученная на основании
выборочного наблюдения, обычно обладает некоторой погрешностью, так как
она основывается на изучении только части элементов выборки. Это
определяет две проблемы, составляющие содержание математической теории
выборки:
как организовать выборочное наблюдение, чтобы полученная информация
достаточно полно отражала генеральную совокупность (проблема
репрезентативности выборки);
как использовать результаты выборки для суждения по ним с наибольшей
надежностью о свойствах и параметрах генеральной совокупности (проблема
оценки).
28.02.2010
Р. Мунипов
38
39.
В силу закона больших чисел можно утверждать, что выборка будетрепрезентативной, если отбор будет носить случайный характер.
Различают повторную и бесповторную выборки. В первом случае отобранный
объект перед отбором следующего возвращается в генеральную совокупность.
Во втором — отобранный в выборку объект не возвращается в генеральную
совокупность. Если выборка составляет незначительную часть генеральной
совокупности, то различие между повторной и бесповторной выборками
стирается.
Случайный отбор может проводиться с помощью датчика таблицы случайных
чисел либо обычной жеребьевкой. Однако строгое соблюдение правил
случайного отбора не всегда осуществимо, так как оно требует четко
ограниченной базы статистического анализа, каковой является генеральная
совокупность. Прибегают к различным приемам неслучайного отбора,
стремясь, однако, приблизиться к условиям случайного.
28.02.2010
Р. Мунипов
39
40.
К приемам извлечения выборки из генеральной совокупности относитсямеханический отбор, при котором элементы генеральной совокупности,
предварительно упорядоченные, отбираются по заранее установленному
правилу, не связанному с вариацией исследуемого признака. Например, можно
фиксировать доход каждого сотого, входящего в метро.
Серийным называют отбор, при котором объекты выбираются из генеральной
совокупности не по одному, а «сериями», которые подвергаются сплошному
обследованию. Например, о продукции предприятия можно судить по
продукции, выпущенной в какие-то конкретные дни месяца.
При типическом отборе объекты отбираются не из всей генеральной
совокупности, а из каждой её «типической» части. Например, население
города можно предварительно классифицировать по социальному статусу
(бизнесмены, чиновники, служащие, рабочие и т.д.). Нередко на практике
применяется комбинированный отбор, при котором сочетаются описанные
выше способы.
28.02.2010
Р. Мунипов
40
41.
Во многих случаях для анализа экономических процессов важен порядокполучения статистических данных. Но при рассмотрении так называемых
перекрестных данных порядок их получения не играет существенной роли.
Кроме того, результаты выборочных значений количественного признака X
генеральной совокупности, записанные в порядке их регистрации, обычно
труднообозримы и неудобны для дальнейшего анализа. Задачей
статистического описания выборки является получение такого её
представления, которое позволит наглядно выявить вероятностные
характеристики. Для этого применяются различные формы упорядочения
данных в выборке — по возрастанию, по совпадающим значениям, по
интервалам и т.п.
28.02.2010
Р. Мунипов
41
42.
При анализе какого-то конкретного показателя X наблюдаемые значенияобычно упорядочивают по неубыванию: x1 x2 xn . Разность между
максимальным и минимальным значениями СВ X называется размахом
выборки
R( X ) max( xi ) min( xi )
xi X
xi X
Пусть количество различных значений в выборке равно k k n . И пусть
значения в выборке упорядочены по возрастанию x1 x2 xk .
Значения xi i 1,k называются вариантами выборки.
Если значение xi встретилось в выборке ni раз, то число ni называется
частотой значения xi , а величина i ni n — относительной частотой
этого значения.
Наблюдаемые значения можно сгруппировать в статистический ряд
X
x1
x2
xk
k
28.02.2010
ni
n1
n2
nk
n
i i
n
n1
n
n2
n
nk
n
Р. Мунипов
n
j 1
k
j
nj
n
n
1
j 1
42
43.
По статистическому ряду можно построить эмпирическую функциюраспределения :
n
F * ( x) x
n
где nx — число значений случайной величины X, меньших, чем х;
n — объем выборки.
Эмпирическая функция распределения обладает свойствами:
1. 0 F * ( x) 1
2. x1 x2 : F * ( x1 ) F * ( x2 )
3. F * ( x) 0 ( x x1 ), F * ( x) 1 ( x xk )
Эмпирическая функция распределения F * ( x) является оценкой функции
распределения F ( x) P( X x) , которая в этом случае называется
теоретической функцией распределения.
28.02.2010
Р. Мунипов
43
44.
Пример Анализируется прибыль Х(%) предприятий отрасли.Обследованы 100 предприятий, данные по которым занесены в следующий
статистический ряд:
X
ni
ni
n
5
10
15
20
25
5
20
40
25
10
0,05
0,20
0,40
0,25
0,10
x 5,
0
0,05
5 x 10,
0,25 10 x 15,
*
F ( x)
0,65 15 x 20,
0,9 20 x 25,
x 25
1
28.02.2010
F * ( x)
1,00
0,90
0,65
0,25
x
0,05
Р. Мунипов
5
10
15
20
25
44
45.
При большом объеме выборки ее элементы могут быть сгруппированы винтервальный статистический ряд. Для этого все п наблюдаемых значений
выборки x1 , x2 , , xn разбивают по k непересекающимся подинтервалов
равной длины h (h — шаг разбиения). Пусть ni — количество наблюдаемых
значений СВ X, попадающих в i-й подинтервал; i ni n — относительная
частота попадания СВ X в i-й подинтервал. Тогда интервальный
статистический ряд имеет вид
xi 1, xi
ni
i
28.02.2010
ni
n
x0 , x1 x1, x2
xk 1, xk
n1
n2
nk
n1
n
n2
n
nk
n
Р. Мунипов
45
46.
Для любой СВ X кроме определения ее функции распределения желательноуказать числовые характеристики, важнейшими из которых являются
математическое ожидание, дисперсия, среднее квадратическое отклонение.
Пусть объем генеральной совокупности равен N. Тогда математическим
ожиданием СВ X является генеральное среднее:
1 N
xà xi
N i 1
Дисперсией СВ Х является генеральная дисперсия:
1 N
2
DÃ xi xÃ
N i 1
Корень квадратный из генеральной дисперсии называется генеральным
средним квадратическим отклонением:
à DÃ
28.02.2010
Р. Мунипов
46
47.
Для нахождения генеральных числовых характеристик необходим анализ всейгенеральной совокупности. В силу того что в реальности чаще всего работают
с выборками, приходится находить оценки указанных выше генеральных
характеристик — выборочные числовые характеристики: выборочное среднее,
выборочную дисперсию, выборочное среднее квадратическое отклонение.
Выборочное среднее — это среднее арифметическое наблюдаемых значений
выборки,
1 n
x xi
n i 1
При задании выборки в виде статистического ряда выборочная средняя
рассчитывается по следующей формуле:
для упрощения будем
1 k
x ni xi
обозначать x через x
n i 1
Оценкой генеральной дисперсии является выборочная дисперсия:
1 n
2
DÂ xi xÂ
n i 1
2
n
n
1 n
1
1
Причём, D xi 2 x 2 2 xi x xi 2 xi x 2 x 2
n i 1
n i 1
n i 1
28.02.2010
Р. Мунипов
47
48.
При задании выборки в виде статистического ряда имеем:1 k
2
DÂ xi x ni
n i 1
Корень квадратный из выборочной дисперсии называется выборочным
средним квадратическим отклонением:
1 k
2
 DÂ
x
x
i ni
n i 1
При задании выборки в виде интервального статистического ряда в формулах
вместо xi рассматривается среднее значение i-го подинтервала:
xi
28.02.2010
xi 1 xi
2
Р. Мунипов
48
49.
Характеристиками связи двух СВ являются меры их линейной связи —ковариация и коэффициент корреляции. Их оценками являются выборочная
ковариация S xy и выборочный коэффициент корреляции rxy :
1 n
S xy xi x yi y xy x y
n i 1
n
rxy
S xy
 ( X )  (Y )
x x y y
i
i 1
n
i
n
x x y y
i 1
2
i
i 1
2
xy x y
x2 x 2 y 2 y 2
i
где
1 n
xy xi yi
n i 1
28.02.2010
Выборочные ковариация и коэффициент
корреляции обладают теми же свойствами, что
и их теоретические прототипы.
Р. Мунипов
49
50.
Статистические выводы — это заключения о генеральной совокупности (т.е.о законе распределения исследуемой СВ и его параметрах либо о наличии и
силе связи между исследуемыми переменными) на основе выборки, случайно
отобранной из генеральной совокупности. Суть статистических выводов в
обобщение результатов, полученных по выборке, на генеральную
совокупность.
При исследовании различных параметров генеральной совокупности на
основе выборки возможно лишь получение оценок этих параметров. Эти
оценки строятся на основе ограниченного набора данных, что влечет за собой
вероятность погрешности. Значения оценок могут изменяться от выборки к
выборке. Процесс нахождения оценок по определенному правилу (формуле)
называется оцениванием. Цель любого оценивания — получение наиболее
точного значения оцениваемой характеристики.
Выделяют два типа оценивания: оценивание вида распределения и оценивание
параметров распределения, и различают два вида оценок — точечные и
интервальные.
28.02.2010
Р. Мунипов
50
51.
Пусть оценивается некоторый параметр наблюдаемой СВ X генеральнойсовокупности. Пусть из генеральной совокупности извлечена
выборка x1 , x2 , , xn объема п, по которой может быть найдена оценка *
параметра . Например, для нормального закона распределения с
плотностью вероятности
1
f ( x)
e
2
( x m )2
2 2
параметрами являются математическое ожидание т и среднее квадратическое
отклонение .
Точечной оценкой * параметра называется числовое значение этого
параметра, полученное по выборке объема п.
Например, оценками т и для СВ X распределённой по нормальному
закону могут быть
1 n
*
m x xi
n i 1
и
1 n
2
*
Â
x
x
i
n i 1
28.02.2010
Р. Мунипов
51
52.
Очевидно, оценка * является функцией от выборки, т.е. * * ( x1, x2 , , xn ) .Так как выборка носит случайный характер, то оценка * является СВ,
принимающей различные значения для различных выборок. Любую
оценку * * ( x1, x2 , , xn ) называют статистикой или статистической
оценкой параметра .
Положительное число такое, что * называется точностью оценки.
Естественно стремление получить по возможности наиболее точную оценку
при данном объеме выборки.
Определим требования, выполнимость которых желательно для того, чтобы
оценка была признана удовлетворительной.
В силу случайности точечной оценки * она может рассматриваться как СВ
со своими числовыми характеристиками — математическим ожиданием M ( * )
*
и дисперсией D( * ) . Чем ближе M ( ) к истинному значению и чем
меньше D( * ) , тем лучше будет оценка * (при прочих равных условиях).
Качество оценки характеризуется: несмещённостью, эффективностью и
состоятельностью.
28.02.2010
Р. Мунипов
52
53.
Оценка * называется несмещенной оценкой параметра , если еёматематическое ожидание равно оцениваемому параметру: M ( * ) .
Отдельная оценка лишь в редких случаях совпадает с соответствующей
характеристикой генеральной совокупности. При «аккуратном» оценивании,
т.е. многократное осуществление выборок одного объема обеспечивает
совпадение среднего значения оценки по всем выборкам с истинным средним
значением генеральной совокупности.
Разность M ( * ) называется смещением или систематической ошибкой
оценивания. Для несмещенных оценок систематическая ошибка равна нулю
Свойство несмещенности оценки является важнейшим, но не единственным.
Существует несколько возможных оценок одного и того же параметра. Какая
из них лучше? Очевидно, выбор будет сделан в пользу той из них, вероятность
совпадения которой с истинным значением оцениваемого параметра выше.
Оценка должна иметь такую плотность вероятности, которая наиболее
«сжата» вокруг истинного значения оцениваемого параметра. И в этом случае
она будет иметь наименьшую среди других оценок дисперсию.
28.02.2010
Р. Мунипов
53
54.
Оценка * называется эффективной оценкой параметра , если еедисперсия D( * ) меньше дисперсии любой другой альтернативной оценки
при одном и том же объеме выборки.
Оценка * называется асимптотически эффективной, если с увеличением
объема выборки ее дисперсия стремится к нулю, т.е.
lim D( n* ) 0
n
Оценка * называется состоятельной оценкой параметра , если n*
сходится по вероятности к при n , т. е. для любого 0 при n
P * 1
Состоятельной называется такая оценка, которая дает истинное значение при
достаточно большом объеме выборки вне зависимости от значений входящих
в нее конкретных наблюдений.
Справедливо:
28.02.2010
lim M ( n* )
n
*
состоятельная оценка параметра
*
lim D( n ) 0
n
Р. Мунипов
54
55.
Оценка 1 эффективнееоценки 2* , т.к. D 1* D 2*
т.е. кривая плотности ближе к
оцениваемой величине .
*
28.02.2010
Оценка * состоятельная, т.к.
с увеличением числа элементов
её математическое ожидание
приближается к оцениваемой
величине.
Р. Мунипов
55
56.
1 nМожно показать, что выборочное среднее x xi является несмещенной
n i 1
и состоятельной оценкой математического ожидания М(Х) генеральной
совокупности.
1 n
2
Выборочная дисперсия D xi x является смещенной оценкой
n i 1
дисперсии D( X ) 2 СВ X генеральной совокупности,
n 1
. Иначе, выборочная дисперсия оценивает генеральную
n
n 1
дисперсию с недостатком. Вместе с тем lim
1 , тогда оценка DB
n n
является асимптотически несмещенной. В качестве оценки дисперсии D(X)
так как DÂ 2
рассматривают исправленную дисперсию:
n
1 n
1 k
2
2
2
S
DÂ
x
x
n
x
x
i Â
i i
Â
n 1
n 1 i 1
n 1 i 1
28.02.2010
Р. Мунипов
56
57.
Исправленная дисперсия S2 является несмещенной и состоятельной оценкойдисперсии D(X) СВ X.
Аналогично вводится исправленное среднее квадратическое отклонение
(эмпирический стандарт S):
1 n
1 k
2
2
S S
x
x
n
x
x
i Â
i i Â
n 1 i 1
n 1 i 1
2
При п > 30 различие между DB и S2 ( Â и S ) практически незначимо,
поэтому при большом объеме выборки и ту, и другую оценки можно считать
несмещенными.
ni
Относительная частота
является несмещенной и состоятельной оценкой
n
вероятности P ( X xi ) . Аналогично эмпирическая функция
nx
(накопленная относительная частота) является
n
несмещенной и состоятельной оценкой (теоретической) функции
распределения F * ( x)
распределения
F ( x ) P( X x ) .
28.02.2010
Р. Мунипов
57
58.
Точечная оценка может быть дополнена интервальной оценкой —интервалом 1 , 2 , внутри которого с наперёд заданной вероятностью
находится точное значение оцениваемого параметра . Задачу определения
такого интервала называют интервальным оцениванием, а сам интервал —
доверительным интервалом. При этом называют доверительной
вероятностью или надежностью, с которой оцениваемый параметр
попадает в интервал 1 , 2 .
Для определения доверительного интервала заранее выбирают число 1 ,
такое, что 0 1 , называемое уровнем значимости, и находят два числа 1
и 2 , зависящих от точечной оценки *, такие, что P 1 2 1
Это означает, что интервал 1 , 2 накрывает неизвестный параметр с
вероятностью 1 , или в 100(1 )% случаев. Границы интервала 1 и 2
называются доверительными, и они обычно находятся из условия
P 1 P 2
28.02.2010
Р. Мунипов
2
58
59.
Длина доверительного интервала, характеризующая точность интервальнойоценки, зависит от объема выборки n и надежности (уровня
значимости 1 ). При увеличении величины n длина доверительного
интервала уменьшается, а с приближением надежности к единице —
увеличивается. Выбор (или 1 ) определяется конкретными
условиями. Обычно используется 0,1; 0,05; 0,01 , что соответствует
90, 95, 99%-м доверительным интервалам.
Общая схема построения доверительного интервала:
1. Из генеральной совокупности с известным распределением f ( x, ) СВ X
извлекается выборка объема п, по которой находится точечная оценка *
параметра .
2. Строится СВ Y ( ) , связанная с параметром и имеющая известную
плотность вероятности f ( y, ) .
3. Задается уровень значимости .
4. Используя плотность вероятности СВ Y, определяют два числа c1 и c2
такие, что
c2
P c1 Y ( ) c2 f ( y, )dy 1
c1
28.02.2010
Р. Мунипов
59
60.
Значения c1 и c2 выбираются, как правило, из условияP Y ( ) c1 P Y ( ) c2
2
Неравенство c1 Y ( ) c2 преобразуется в равносильное * *
такое, что
P * * 1
Полученный интервал * , * , накрывающий неизвестный параметр
с вероятностью 1 , является интервальной оценкой параметра .
Интервальная оценка имеет случайный характер, так как она связана с
результатами выборки. Если построен доверительный интервал, который с
надежностью 1 накрывает неизвестный параметр, и его границы
рассчитываются по K выборкам одинакового объема n , то в (1 )K
случаях построенные интервалы накроют истинное значение исследуемого
параметра.
28.02.2010
Р. Мунипов
60
61.
Пусть количественный признак X генеральной совокупности имеетнормальное распределение с заданной дисперсией 2 и неизвестным
математическим ожиданием m X N (m, ) . Построим доверительный
интервал для т.
1.
Пусть для оценки т извлечена выборка x1 , x2 ,
, xn объема п,
1 n
тогда m xi x
n i 1
x m
2. Составим СВ U i
. Очевидно, СВ U имеет стандартизированное
n
u2
1 2
нормальное распределение, т.е. U N (0,1) f (u )
e
2
3. Зададим уровень значимости .
*
4.
Применяя формулу нахождения вероятности отклонения нормальной
величины от математического ожидания, имеем:
x m
P U u P
u P x u
m x u
1
n
n
2
2
2
2
n
28.02.2010
Р. Мунипов
61
62.
; x uЗначит доверительный интервал x u
накрывает
n
n
2
2
неизвестный параметр т с надежностью 1 . Точность оценки
определяется величиной u
2
n
.
Число u определяется по таблице значений функции Лапласа из равенства
2
1
Ô u
2
2
2
28.02.2010
Р. Мунипов
62
63.
В реальности истинное значение дисперсии исследуемой СВ, скорее всего,известно не будет. Это приводит к необходимости использования другой
формулы при определении доверительного интервала для математического
ожидания СВ, имеющей нормальное распределение.
Пусть X N (m, 2 ) , причем т и 2 — неизвестны. Необходимо построить
доверительный интервал, накрывающий с надежностью 1 истинное
значение параметра т.
Для этого из генеральной совокупности СВ X извлекается выборка x1 , x2 , , xn
объема п.
28.02.2010
Р. Мунипов
63
64.
1.В качестве точечной оценки математического ожидания т используется
1 n
выборочное среднее x xi , а в качестве оценки дисперсии 2 —
n i 1
1 n
2
2
исправленная выборочная дисперсия S
x
x
i  , которой
n 1 i 1
соответствует стандартное отклонение S S 2 .
2.
Для нахождения доверительного интервала строится статистика
xi m
с числом степеней
S n
свободы n 1 независимо от значений параметров m и 2 .
распределения Стьюдента T
3.
Задается требуемый уровень значимости .
4.
Применяется следующая формула расчета вероятности
P T t P t T t 1
,n 1
,n 1
2
2 ,n 1
2
28.02.2010
Р. Мунипов
64
65.
где t2
,n 1
- критическая точка распределения Стьюдента, которая находится по
соответствующей таблице, тогда
x m
P t T t P t
t
,n 1
2 ,n 1
2
2 ,n 1 S n 2 ,n 1
P x t S
,n 1
2
n m x t
2
,n 1
S
n 1
Это означает, что интервал x t S n ; x t S
,n 1
, n 1
2
2
неизвестный параметр т с надежностью 1 .
28.02.2010
Р. Мунипов
n накрывает
65
66.
Пусть X N (m, 2 ) , причем т и — неизвестны. Необходимо построитьдоверительный интервал, накрывающий с надежностью 1 истинное
2
значение параметра .
Для этого из генеральной совокупности СВ X извлекается выборка x1 , x2 , , xn
объема п.
2
28.02.2010
Р. Мунипов
66
67.
1.В качестве точечной оценки дисперсии D(X) используется исправленная
1 n
2
выборочная дисперсия S
x
x
i  , которой соответствует
n 1 i 1
стандартное отклонение S S 2 .
2
2.
Для нахождении доверительного интервала для дисперсии вводится
статистика 2
(n 1) S 2
2
2
, имеющая – распределение с числом
степеней свободы n 1 независимо от значения параметра 2 .
3.
Задается требуемый уровень значимости 1 .
4.
2
Используя таблицу критических точек – распределения, можно указать
2
2
критические точки 1 ,n 1 , ,n 1 , для которых будет выполняться
2
2
равенство: P 2 2 2 1
, n 1
1 2 ,n 1
2
28.02.2010
Р. Мунипов
67
68.
Подставив вместо 2 , соответствующее значение, получим2
2
(n 1) S 2
2
2
2
P P
2
1 ,n 1
,n 1
1 ,n 1
, n 1
2
2
2
2
2
2
(n 1) S
(n 1) S
P 2
2
1
2
1 ,n 1
,n 1
2
2
Очевидно,
(n 1) S 2
2
2
1 ,n 1
2
(n 1) S 2
2
2
S
,n 1
(n 1)
2
1 ,n 1
2
S
(n 1)
2
2
,n 1
2
2
( n 1) S ( n 1) S
;
Таким образом, доверительный интервал 2
2
накрывает
1 ,n 1
, n 1
2
2
неизвестный параметр 2 с надежностью 1 . А доверительный
2
; S (n 1) с надежностью 1
1 ,n 1
, n 1
2
2
накрывает неизвестный параметр .
интервал S (n 1) 2
28.02.2010
Р. Мунипов
68
69.
Эконометрические модели требуют многократного улучшения и уточнения.Для этого необходимо проведение соответствующих расчетов, связанных с
установлением выполнимости или невыполнимости тех или иных
предпосылок, анализом качества найденных оценок, достоверностью
полученных выводов. Обычно эти расчеты проводятся по схеме
статистической проверки гипотез.
Во многих случаях необходимо знать закон распределения генеральной
совокупности. Если закон распределения неизвестен, но есть основания
предположить, что он имеет определенный вид (например вид А), выдвигают
гипотезу: генеральная совокупность (СВ X) распределена по закону А.
Возможен случай, когда закон распределения известен, а его параметры
неизвестны. Если есть основания предположить, что неизвестный параметр
равен ожидаемому числу 0 , выдвигают гипотезу: 0 .
Статистической называют гипотезу о виде закона распределения или о
параметрах известного распределения. В первом случае гипотеза называется
непараметрической, а во втором — параметрической.
28.02.2010
Р. Мунипов
69
70.
Гипотеза H 0 , подлежащая проверке, называется нулевой (основной).Рассматривают также гипотезу H 1 , которая будет приниматься, если H 0
отклоняется . Такая гипотеза H 1 называется альтернативной
(конкурирующей). Например, если проверяется гипотеза о равенстве
параметра некоторому значению 0 , т.е. H 0 : 0 , то в качестве
альтернативной могут рассматриваться следующие гипотезы:
H1(1) : 0 , H1(2) : 0 , H1(3) : 0 , H1(4) : 1 1
Выбор альтернативной гипотезы определяется конкретной формулировкой
задачи, а нулевая гипотеза часто специально так, чтобы отвергнуть ее и
принять тем самым альтернативную гипотезу.
Гипотезу называют простой, если она содержит одно конкретное
предположение . Гипотезу называют сложной, если она состоит из конечного
или бесконечного числа простых гипотез
H
28.02.2010
(1)
1
: 0 , H1(2) : 0 , H1(3) : 0
Р. Мунипов
70
71.
Сущность проверки статистической гипотезы заключается в том, чтобыустановить, согласуются или нет данные наблюдений и выдвинутая гипотеза.
Можно ли расхождение между гипотезой и результатом выборочных
наблюдений отнести за счет случайной погрешности, обусловленной
механизмом случайного отбора? Эта задача решается с помощью специальных
методов математической статистики — методов статистической проверки
гипотез.
При проверке гипотезы выборочные данные могут противоречить
гипотезе H 0 . Тогда она отклоняется. Если же статистические данные
согласуются с выдвинутой гипотезой, то она не отклоняется. В последнем
случае часто говорят, что нулевая гипотеза не отклоняется. Статистическая
проверка гипотез на основании выборочных данных связана с риском
принятия ложного решения. При этом возможны ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая
гипотеза.
Ошибка второго рода состоит в том, что будет принята нулевая гипотеза, в то
время как в действительности верна альтернативная гипотеза.
28.02.2010
Р. Мунипов
71
72.
Возможные состоянияПоследствия указанных
Результаты
гипотезы
ошибок неравнозначны.
проверки гипотезы
Первая приводит к более
Верна H 0
Верна H 1
Обычно значения задают заранее,
«круглыми»
числами (например, 0,1;
осторожному,
Гипотеза
Ошибка
Правильный
0,05;
0,01 иHт.п.),
т.е. стремятся
построить
критерий наибольшей мощности.
0
отклоняется
первого рода
вывод не консервативному
Если
что исследователь
хочет совершить ошибку
0,05 то, это означает,
решению, вторая — к
первого
рода
в 5 случаях из 100.
Гипотеза
не чем Правильный
Ошибка
H 0более
неоправданному риску.
отклоняется
вывод
второго рода
Исключить ошибки первого и второго рода невозможно в силу
ограниченности выборки. Стремятся минимизировать потери от этих ошибок.
Одновременное уменьшение вероятностей данных ошибок невозможно, так
как задачи их уменьшения являются конкурирующими, и снижение
вероятности допустить одну из них влечет за собой увеличение вероятности
допустить другую. В большинстве случаев единственный способ уменьшения
вероятности ошибок состоит в увеличении объема выборки.
Вероятность совершить ошибку первого рода принято обозначать через , и
ее называют уровнем значимости. Вероятность совершить ошибку второго
рода обозначают . Вероятность не совершить ошибку второго рода (1 )
называется мощностью критерия.
28.02.2010
Р. Мунипов
72
73.
Проверку статистической гипотезы 2 осуществляют на основании данныхвыборки. Для этого используют специально подобранную СВ (статистику,
критерий), точное или приближенное значение которой известно. Эту
величину обозначают:
1. U (или Z) — если она имеет стандартизированное нормальное
распределение;
2.
Т — если она распределена по закону Стьюдента;
2
2
3. — если она распределена по закону ;
4. F — если она имеет распределение Фишера.
Будем обозначать такую СВ через К.
Таким образом, статистическим критерием называют СВ К, которая служит
для проверки нулевой гипотезы. После выбора определенного критерия
множество всех его возможных значений разбивают на два непересекающихся
подмножества: одно из них содержит значения критерия, при которых нулевая
гипотеза отклоняется, другое — при которых она не отклоняется.
Совокупность значений критерия, при которых нулевую гипотезу отклоняют,
называют критической областью. Совокупность значений критерия, при
которых нулевую гипотезу не отклоняют, называют областью принятия
гипотезы.
28.02.2010
Р. Мунипов
73
74.
Основной принцип проверки статистических гипотез можно сформулироватьтак: если наблюдаемое значение критерия К (вычисленное по выборке)
принадлежит критической области, то нулевую гипотезу отклоняют. Если же
наблюдаемое значение критерия К принадлежит области принятия гипотезы,
то нулевую гипотезу не отклоняют (принимают).
Точки, разделяющие критическую область и область принятия гипотезы,
называют критическими.
28.02.2010
Р. Мунипов
74
75.
Пусть для проверки нулевой гипотезы H 0 служит критерий К. Пустьплотность распределения вероятности СВ К в случае справедливости H 0
имеет вид f (k , H 0 ) , а математическое ожидание К равно k 0 . Тогда
вероятность того, что СВ К попадет в произвольный интервал k , k
1 2 2
исчисляется по формуле
k
2
P k K k f (k , H 0 )dk
1 2
2
k
1
2
28.02.2010
Р. Мунипов
75
76.
Зададим эту вероятность равной 1 и вычислим критические точки(квантили) k
1
2
, k K-распределения из условий:
2
k
2
P K k f (k , H 0 )dk
1
2
2
k
1
2
k
2
P K k f (k , H 0 )dk
2
2
k
1
2
Следовательно,
P k K k 1 ,
1 2
2
P K k K k
1
2
2
28.02.2010
Р. Мунипов
76
77.
Пусть вероятность настолько мала (0,05; 0,01), что попадание СВ К запределы интервала k1 2 , k 2 можно считать маловероятным событием.
Тогда, исходя из принципа практической невозможности маловероятных
событий, можно считать, что если H 0 справедлива, то при ее проверке с
помощью критерия К по данным одной выборки наблюдаемое значение К
должно наверняка попасть в интервал k1 2 , k 2 . Если же наблюдаемое
значение К попадает за пределы указанного интервала, то произойдет
маловероятное, практически невозможное событие. Это дает основание
считать, что с вероятностью 1 нулевая гипотеза H 0 несправедлива.
Точки k1 2 , k 2 называют критическими.
Критическая область , k1 2 k 2 , называется двусторонней
критической областью , эта область определяется в случае, когда
альтернативная гипотеза имеет вид: H1 : 0 .
28.02.2010
Р. Мунипов
77
78.
Правосторонней называют критическую область , определяемую изсоотношения P K k . Она используется в случае, когда
альтернативная гипотеза имеет вид: H1 : 0
Левосторонней называют критическую область , определяемую из
соотношения P K k1 . Она используется в случае, когда
альтернативная гипотеза имеет вид: H1 : 0
28.02.2010
Р. Мунипов
78
79.
Общая схема проверки гипотез:1. Формулировка проверяемой (нулевой — H 0 ) и альтернативной ( H 1 )
гипотез.
2. Выбор соответствующего уровня значимости .
3. Определение объема выборки п.
4. Выбор критерия К для проверки H 0 .
5. Определение критической области и области принятия гипотезы.
6. Вычисление наблюдаемого значения критерия K í àáë
7. Принятие статистического решения.
Проверка гипотез и доверительные интервалы. Проверка гипотез при
двусторонней критической области тесно связана с интервальным
оцениванием. При одном и том же уровне значимости и объеме выборки п
попадание гипотетического значения исследуемого параметра в
доверительный интервал равносильно попаданию соответствующего критерия
в область принятия гипотезы. Поэтому для проверки гипотезы в этом случае
используют доверительный интервал. Если гипотетическое значение
исследуемого параметра попадает в этот интервал, то делают вывод, что нет
оснований для отклонения выдвигаемой гипотезы.
28.02.2010
Р. Мунипов
79
80.
Пусть генеральная совокупность X распределена нормально, X N (m, 2 ) ,причем ее математическое ожидание т неизвестно, а дисперсия 2 известна.
Предполагается , что m m0 , тогда
H 0 : m m0 ,
H1(1) : m m0 H1(2) : m m0 , H1(3) : m m0
Для проверки H 0 извлекается выборка объема п: x1 , x2 ,
критерия строится статистика
x m
U
n
, xn и в качестве
1 n
1 n
2
где x xi , ( xi x ) 2.
n i 1
n i 1
Статистика U имеет стандартизированное нормальное распределение
U
28.02.2010
N (0,1)
Р. Мунипов
80
81.
1.Пусть в качестве альтернативной рассматривается гипотеза H1(1) : m m0 .
Тогда критические точки u 2 и u1 2 u 2 будут определяться по
таблице значений функции Лапласа из условия
Ô (u 2 )
1
2
x m0
u 2 — нет оснований для отклонения H 0 .
n
Если U í àáë u 2 гипотеза H 0 отклоняется в пользу альтернативной H1(1).
2. При H1(2) : m m0 критическую точку u правосторонней критической
области находят из равенства
1 2
Ô (u )
2
Если U í àáë u — нет оснований для отклонения H 0 .
Если U í àáë u — отклоняют H 0 в пользу H1(2).
Если U набл
3.
При H1(3) : m m0 критическая точка u1 u .
Если U í àáë u1 — нет оснований для отклонения H 0 .
Если U í àáë u1 — отклоняют H 0 в пользу H1(3) .
28.02.2010
Р. Мунипов
81
82.
Пусть генеральная совокупность X распределена нормально, X N (m, 2 ) ,причем её математическое ожидание т и дисперсия 2 неизвестны.
Предполагается , что m m0 , тогда
H 0 : m m0 ,
H1(1) : m m0 H1(2) : m m0 , H1(3) : m m0
Для проверки H 0 извлекается выборка объема п: x1 , x2 , , xn и в качестве
критерия строится t-статистика с n 1 степенями свободы
x m0
T
S n
1 n
1 n
2
2
где x xi выборочная средняя, S
есть исправленная
(
x
x
)
i
n i 1
n 1 i 1
выборочная дисперсия, S S 2 есть стандартное отклонение.
28.02.2010
Р. Мунипов
82
83.
1.При H1(1) : m m0 по таблице критических точек распределения
Стьюдента для заданного уровня значимости и числу степеней
свободы n 1 находятся критические точки t 2,n 1 и t1 2,n 1 t 2,n 1 .
Если
Если
2.
(1)
гипотеза H 0 отклоняется в пользу альтернативной H1 .
При H1(2) : m m0 определяют критическую точку t ,n 1 правосторонней
критической области.
Если
Если
3.
— нет оснований для отклонения H 0 .
— нет оснований для отклонения H 0 .
— отклоняют H 0 в пользу H1(2).
При H1(3) : m m0 определяют критическую точку t1 ,n 1 t ,n 1
левосторонней критической области.
Если
Если
28.02.2010
— нет оснований для отклонения H 0 .
— отклоняют H 0 в пользу H1(3) .
Р. Мунипов
83
84.
Принятие того или иного решения в экономике часто связано с исследованиемразброса возможных результатов. Такую оценку можно осуществлять на базе
анализа дисперсии СВ. При изучении многих экономических проблем
приходится иметь дело с выдвижением и проверкой гипотез о величине
дисперсии. Одной из распространенных является гипотеза о величине
дисперсии нормальной СВ.
Пусть СВ X N (m, 2 ) ; m, 2 неизвестны. Проверяется гипотеза о
равенстве дисперсии 2 нормально распределенной генеральной
совокупности X гипотетическому (предполагаемому) значению 02 . Тогда,
H 0 : 2 02 ,
H1(1) : 2 02 H1(2) : 2 02 , H1(3) : 2 02
Для проверки H 0 извлекается выборка объема п: x1 , x2 , , xn ; вычисляются
выборочная средняя x и исправленная выборочная дисперсия S 2
1 n
1 n
2
2
x xi , S
(
x
x
)
i
n i 1
n 1 i 1
(n 1) S 2
2
и в качестве критерия проверки H 0 строится статистика
02
с n 1 степенями свободы.
28.02.2010
Р. Мунипов
84
85.
1.При справедливости H 0 по таблице критических
2
точек -распределения по заданному уровню значимости и числу
2
степеней свободы n 1 находят критические точки 1 2,n 1
2
и 2,n 1 двусторонней критической области.
Если
Если
2.
(1)
отклоняется H 0 в пользу H1
или
2
При H1(2) : 2 02 определяют критическую точку ,n 1
правосторонней критической области.
Если
Если
3.
— нет оснований для отклонения H 0 .
— нет оснований для отклонения H 0 .
— отклоняют H 0 в пользу H1(2) .
2
При H1(3) : 2 02 определяют критическую точку 1 ,n 1
левосторонней критической области.
Если
Если
28.02.2010
— нет оснований для отклонения H 0 .
— отклоняют H 0 в пользу H1(3).
Р. Мунипов
85
86.
При анализе многих экономических показателей приходится сравнивать двегенеральные совокупности. В этих случаях проверяют равенство
математических ожиданий двух генеральных совокупностей X и Y.
Пусть X N (mx , x2 ) и Y N (my , y2 ) , причём их дисперсии x2 и y2
известны (например, из предшествующих наблюдений или определены
теоретически). По двум выборкам x1 , x2 , , xn и y1 , y2 , , yk объемов п и k
соответственно необходимо проверить гипотезу M(X)=M(Y), т.е.
H 0 : M ( X ) M (Y ),
H1(1) : M ( X ) M (Y ) H1(2) : M ( X ) M (Y ), H1(3) : M ( X ) M (Y )
В качестве критерия проверки H 0 принимается СВ U :
U
x y
x2
n
При справедливости H 0 СВ U
28.02.2010
14.02.2010
y2
k
N (0,1)
Р. Мунипов
86
87.
1.При H 0 по таблице функции Лапласа определяют две критические
точки u 2 и u1 2 из условий:
Ô (u 2 )
Если U í àáë u
Если U í àáë u
2.
2
2
1
, u1 2 u 2
2
— нет оснований для отклонения H 0 .
гипотеза H 0 отклоняется в пользу альтернативной H1(1).
При H1(2) : M ( X ) M (Y ) критическую точку u правосторонней
критической области находят из равенства
Ô (u )
1 2
2
Если U í àáë u — нет оснований для отклонения H 0 .
Если U í àáë u — отклоняют H 0 в пользу H1(2) .
3.
При H1(3) : M ( X ) M (Y ) критическая точка u1 левосторонней
критической области определяется из соотношения u1 u .
Если U í àáë u1 — нет оснований для отклонения H 0 .
Если U í àáë u1 — отклоняют H 0 в пользу H1(3).
28.02.2010
Р. Мунипов
87
88.
Более реалистичным является случай, когда дисперсии рассматриваемых СВнеизвестны.
Пусть X N (mx , x2 ) и Y N (my , y2 ) , причём их дисперсии x2 и y2
неизвестны. По двум выборкам x1 , x2 , , xn и y1 , y2 , , yk объемов п и k
соответственно необходимо проверить гипотезу M(X)=M(Y), т.е.
H 0 : M ( X ) M (Y ),
H1(1) : M ( X ) M (Y )
H
(2)
1
: M ( X ) M (Y ), H1(3) : M ( X ) M (Y )
В качестве критерия проверки H 0 принимается СВ T :
T
x y
(n 1) S x2 (k 1) S y2
nk (n k 2)
n k
1 n
1 n
1 k
1 k
2
2
2
где x xi , S x
( xi x ) , y yi , S y
( yi y ) 2
n i 1
n 1 i 1
k i 1
k 1 i 1
При справедливости H 0 статистика Т имеет t-распределение
Стьюдента c n k 2 степенями свободы.
28.02.2010
Р. Мунипов
88
89.
1.2.
При H1(1) : M ( X ) M (Y ) по таблице критических точек распределения
Стьюдента для заданного уровня значимости и числу степеней
свободы n k 2 находятся критические точки t 2,n k 2 и t1 2,n k 2
двухсторонней критической области, причем t1 2,n k 2 t 2,n k 2 .
Если Tí àáë t
2,n k 2
— нет оснований для отклонения H 0 .
Если Tí àáë t
2,n k 2
гипотеза H 0 отклоняется в пользу H1(1)
При H1(2) : M ( X ) M (Y ) определяют критическую точку t ,n k 2
правосторонней критической области.
Если Tí àáë t ,n 1 — нет оснований для отклонения H 0 .
(2)
Если Tí àáë t ,n 1 — отклоняют H 0 в пользу H1 .
3.
При H1(3) : M ( X ) M (Y ) определяют критическую
точку t1 ,n k 2 t ,n k 2 левосторонней критической области.
H0
Если Tí àáë t ,n k 2 — нет оснований для отклонения
.
Если Tí àáë t ,n k 2 — отклоняют H 0 в пользу H1(3) .
28.02.2010
Р. Мунипов
89
90.
При сравнении двух экономических показателей возникает необходимостьанализа разброса значений рассматриваемых СВ, что осуществляют путём
сравнения дисперсий исследуемых СВ.
Пусть X N (mx , x2 ) и Y N (my , y2 ) , причём их дисперсии x2 и y2
неизвестны. По двум выборкам x1 , x2 , , xn и y1 , y2 , , yk объемов п и k
соответственно проверяют гипотезу x2 y2 т.е.
H 0 : x2 y2 ,
H1(1) : M ( X ) M (Y )
H
(2)
1
: x2 y2
(для определённости предполагается, что S x2 S y2 , в противном случае
можно выполнить переобозначение).
В качестве критерия проверки H 0 принимается СВ F :
S x2
F 2
Sy
1 n
1 n
1 k
1 k
2
2
2
2
где x xi , Sx
(
x
x
)
,
y
y
,
S
(
y
y
)
i
i y k 1
i
n i 1
n 1 i 1
k i 1
i 1
При справедливости H 0 статистика F имеет F-распределение Фишера
c 1 n 1 и 2 k 1 степенями свободы.
28.02.2010
Р. Мунипов
90
91.
1.2.
При H1 : x y по таблице критических точек распределения Фишера
для заданного уровня значимости и числу степеней свободы 1 , 2
определяют критическую точку F 2, 1 , 2 .
(1)
2
2
Если Fí àáë F 2, 1 , 2
— нет оснований для отклонения H 0 .
Если Fí àáë F 2, 1 , 2
гипотеза H 0 отклоняется в пользу H1(1)
При H1(2) : x2 y2 определяют критическую точку F , 1 , 2
Если Fí àáë F , 1 , 2 — нет оснований для отклонения H 0 .
(2)
Если Fí àáë F , 1 , 2 — отклоняют H 0 в пользу H1 .
28.02.2010
Р. Мунипов
91
92.
Одним из важнейших элементов эконометрического анализа являетсяустановление наличия связи между различными показателями. Обычно анализ
начинают с простейшей — линейной зависимости. Для того чтобы установить
наличие значимой линейной связи между двумя СВ X и Y, следует проверить
гипотезу о статистической значимости коэффициента корреляции.
В этом случае используется следующая гипотеза:
H 0 : xy 0,
H1(1) : xy 0
Для проверки H 0 по выборке ( x1 , y1 ),( x2 , y2 ),
статистика
rxy n 2
T
1 rxy2
,( xn , yn ) объема п строится
где rxy — выборочный коэффициент корреляции.
При справедливости статистика Т имеет распределение Стьюдента с n 2
степенями свободы.
28.02.2010
Р. Мунипов
92
93.
По таблице критических точек распределения Стьюдента по заданномууровню значимости и числу степеней свободы n 2 определяем
критическую точку t 2,n 2 .
Если
Tí àáë t 2,n 2 — нет оснований для отклонения H 0 .
Если
Tí àáë t 2,n 2 гипотеза H 0 отклоняется в пользу H1(1)
Если H 0 отклоняется, то фактически это означает, что коэффициент
корреляции статистически значим (существенно отличен от нуля).
Следовательно, X и Y — коррелированы, т.е. между ними существует
линейная связь.
28.02.2010
Р. Мунипов
93




























































































 Математика
Математика Экономика
Экономика








