Вычисление собственных чисел и собственных векторов

1. Тема. Вычисление собственных чисел и собственных векторов

Постановка задачи:
Axi = λixi
Квадратная матрица n n имеет m
различных собственных чисел λi и
соответствующих им собственных
векторов xi кратности ki,
m
k
i 1
i
n, i 1, 2,..., n, 1 m n

2. Вычисление собственных чисел и векторов

Идея:
Axi – λixi = 0
(A– λiE)xi = 0
det(A– λiE) = 0
det A i E D i a0 a1 i a ... 0,
n
или D i 1 in 1 in 1 2 in 2 ... 1 n ,
2
2 i
где i – сумма всех диагональных
миноров порядка i.
n
i
n

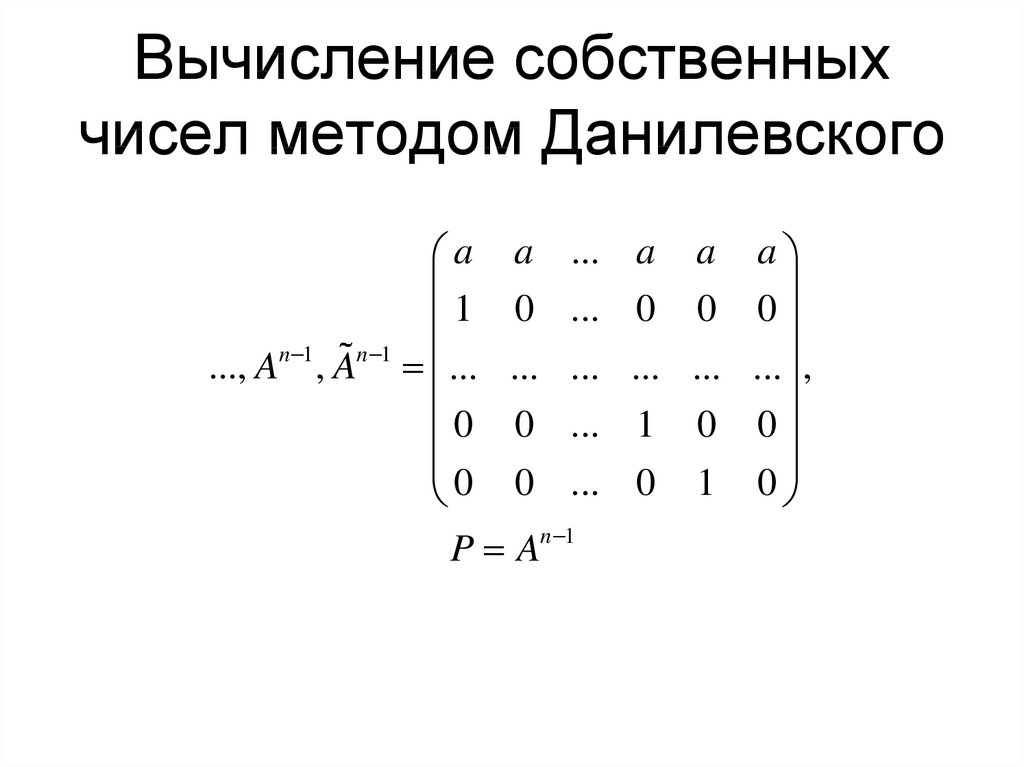
3. Вычисление собственных чисел методом Данилевского

Матрица Фробениуса:
p1
1
P
...
0
p2 ...
pn 1
0
...
...
...
0
...
0
0
1
pn
0
...
0
Тогда D(λi) = det(P – λiE) = (–1)n[λin – p1λin–1 –
p2λin–2 – … – pn]

4. Вычисление собственных чисел методом Данилевского

Преобразование подобия:
P S 1 AS
det P i E det A i E
S M n 1M n 2 ...M 1 , S 1 M 1 1M 2 1...M n 11
A k M n 1k A k 1 M n k , k 1, 2,..., n 1,
0
A
n 1
A, P A

5. Вычисление собственных чисел методом Данилевского

m e , i 1, 2,..., n, j 1, 2,..., n, i k ;
ij
ij
n k 1
a
k 1, j
M k : mkj n k 1 , j 1, 2,..., n, j k ;
ak 1,k
1
mkk n k 1 .
ak 1,k
mij eij , i 1, 2,..., n, j 1, 2,..., n, i k ;
M k 1 :
n k 1
mkj ak 1, j , j 1, 2,..., n.

6. Вычисление собственных чисел методом Данилевского

A A
k
a
a
A1 , A1 : ...
a
0
k 1
M n k , A M n 1k A , k 1, 2,..., n 1
k
k
a
a
a
a
... ... ... ... ... , A2 , A2 : ...
a ... a a a
0
0
0 ... 0 1 0
a ... a
a ... a
a
a
a
a
... ... ... ... ... ,
0 ... 1 0 0
0 ... 0 1 0
a ... a
a ... a
a
a

7. Вычисление собственных чисел методом Данилевского

a a ...
1 0 ...
..., An 1 , An 1 ... ... ...
0 0 ...
0 0 ...
P An 1
a
0
... ... ... ,
1 0 0
0 1 0
a
0
a
0

8. Вычисление собственных векторов

Имеем СЛАУ:
(A– λiE)xi = 0,
det(A– λiE) = 0
Вариант Данилевского:
(P– λiE)yi = 0,
xi = Syi, i = 1, 2, …, n
Здесь yi – собственный вектор матрицы
P, xi – собственный вектор матрицы A.

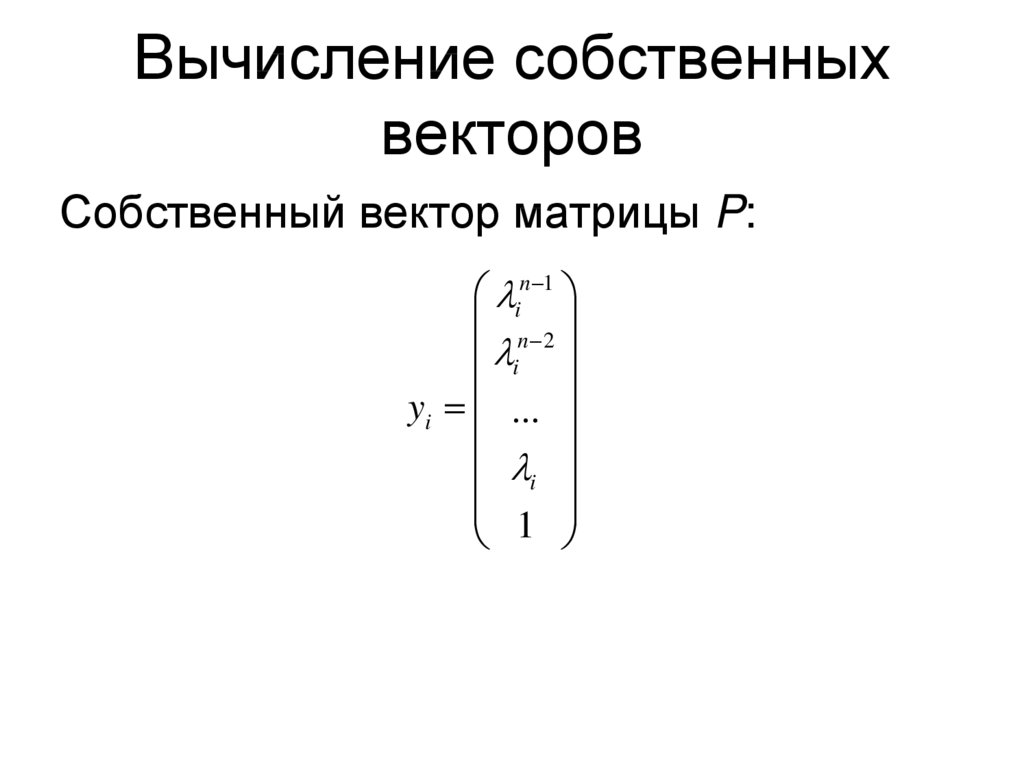
9. Вычисление собственных векторов

Собственный вектор матрицы P:
in 1
n 2
i
yi ...
i
1

10. Пример

1 3 4
A 4 7 8
6 7 7
n 3
A E P E 1 3 p11 2 p12 p13 0
P S 1 AS M 1 1M 2 1 AM 2 M 1
3
A0 A; Ai M 3 1i Ai 1M 3 i , i 1, 2
y , ,1
2
T
x Sy M 2 M 1 y

11. Пример

mi ei
m ei
1 i
(0)
M2 :
M2 :
a3 j
1
(0)
m
,
m
m
a
2
2j
3
22 a (0)
(0)
a32
32
1 0 0
1 3 4
1 0 0
6
1
0
A 4 7 8 , M 2
1 , M 2 1 6 7 7
7
7
6 7 7
0 0 1
0 0 1

12. Пример

1
1 3 4
6
0
A 4 7 8 , M 2
7
6 7 7
0
11
7
1
0
A A M 2 2
0
3
1
7
1 1 ,
1 0
0
1
7
0
0
1 0 0
1
1 , M 2 6 7 7
0 0 1
1
11 3
1
7 7
32 18
1
1 1
A M2 A
1
7
7
1 0
0

13. Пример

mi ei
mi ei
1
(1)
M1 :
a2 j M 1 :
1
(1)
m
,
m
m
a
1j
1
2
11 a (1)
(1)
a21
21
11 3
18 7
7
32 18
7 7 1
7
32
32 32
7
32 18
1
1
A
1 , M 1 0
1
0 , M1 0
1
7
7
0
0
0
1
0
0
1
0
1
0
1

14. Пример

11 3
7 7
32 18
1
A
7
7
1
0
1
18 7
7
32
7
32
32 32
1
1 , M 1 0
1
0 , M1 0
0
0
0
1
0
11 42 21
32 32 32
1 5
2
1
A A M1 1
0
0 , A2 M 1 1 A2 1 0
0 1
0
1
0
18
7
1
0
1
0
1
3
0 P
0

15. Пример

1 5 3
P 1 0 0
0 1 0
D P E 1 3 2 5 3 3 2 5 3 0
3
p( x a )( x b)( x c) p x 3 (a b c) x 2 (ab ac bc) x abc
1 1
D p 1 2 a b

16. Пример

3
3
2
2
2 2
5
2 2
2
3
3
1
3
2 2 3
5
3
3
0
2 2 3 0
2 1, 3 3
D 1 3
2

17. Пример

y , ,1
2
T
x Sy M 2 M 1 y
y1 y2 12 , 1 ,1 22 , 2 ,1 1, 1,1
y3 32 , 3 ,1 9,3,1
7 18 7
7 18 7
1 0 0
32
32
32
32 32 32
6 1
6 20 38
S M 2 M1 1 0 1 0
7 7
32
32
32
0 0 1 0 0 1 0 0 1

18. Пример

7 18 7
32 32 32
1 1
6 20 38
x1 x2 Sy1 Sy2
1 2
32 32 32
1 1
0 0 1
7 18 7
32 32 32
9 1 2
6 20 38
x3 Sy3
3 1
32 32 32
1 1
0 0 1