Похожие презентации:
Собственные значения, собственные векторы матрицы
1. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
СОБСТВЕННЫЕ ЗНАЧЕНИЯ,СОБСТВЕННЫЕ ВЕКТОРЫ
МАТРИЦЫ
2. Собственные значения матрицы
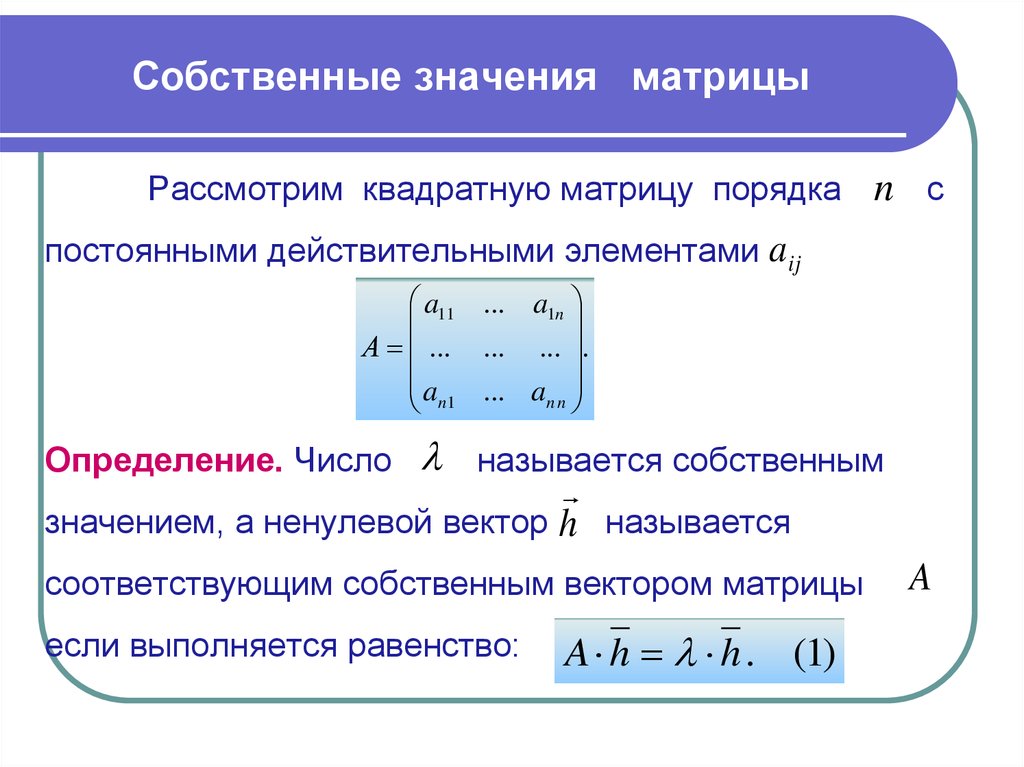
Рассмотрим квадратную матрицу порядка n спостоянными действительными элементами a ij
a11 ... a1n
А ... ... ... .
a
...
a
nn
n1
называется собственным
значением, а ненулевой вектор h называется
Определение. Число
соответствующим собственным вектором матрицы
если выполняется равенство:
A h h . (1)
A
3. Собственные значения матрицы
Определение. Множество всех собственных значенийматрицы называется спектром матрицы.
Замечание.
Представим равенство (1) в сл. виде:
Ah h 0;
или ( A E ) h 0,
( 2)
E единичная матрица порядка n . Равенство (2)
является системой линейных алгебраических
уравнений относительно вектора h .
4. Собственные значения матрицы
Система вида (2) всегда совместна, так как всегдаимеет нулевое решение.
Система (2) имеет тривиальное (нулевое h 0 )
решение, если определитель матрицы
Система (2) имеет ненулевые решения
A E 0.
(3)
A E 0;
h 0 , если
5. Собственные значения матрицы
Уравнение (3) называется характеристическимуравнением матрицы
A.
Решения уравнения (3) называются собственными
значениями матрицы
A.
Уравнение (3) можно представить в сл. виде
(a11 )
a 21
a12
...
a1 n
(a 22 ) ...
a2 n
...
...
a n1
an 2
...
...
... (a n n )
0
6. Собственные значения матрицы
Вычислив определитель,первой
строки,
и
разложив его по элементам
сгруппировав
подобные
члены,
получим алгебраическое уравнение степени n
n b1 n 1 b2 n 2 . . . bn 0
относительно
, а
действительные числа
b1 , b2 ,. . ., bn
где постоянные
bn ( 1) n A .
Многочлен n ой степени относительно
называется
характеристическим многочленом матрицы
A.
7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Согласноосновной
теореме
алгебры
характеристическое уравнение всегда имеет ровно
n (с учетом их кратности), которые в общем
корней
случае являются комплексными числами.
Теорема. Любая постоянная квадратная матрица
порядка
n
имеет с учетом кратности ровно n
собственных значений, совпадающих с корнями
характеристического уравнения.
A
8. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Замечание. Задача нахождения собственныхзначений матрицы A сводится к решению
характеристического уравнения .
Пример. Найти собственные значения и векторы
матрицы
1 4
A
.
9 1
Решение. Составляем характеристическое уравнение
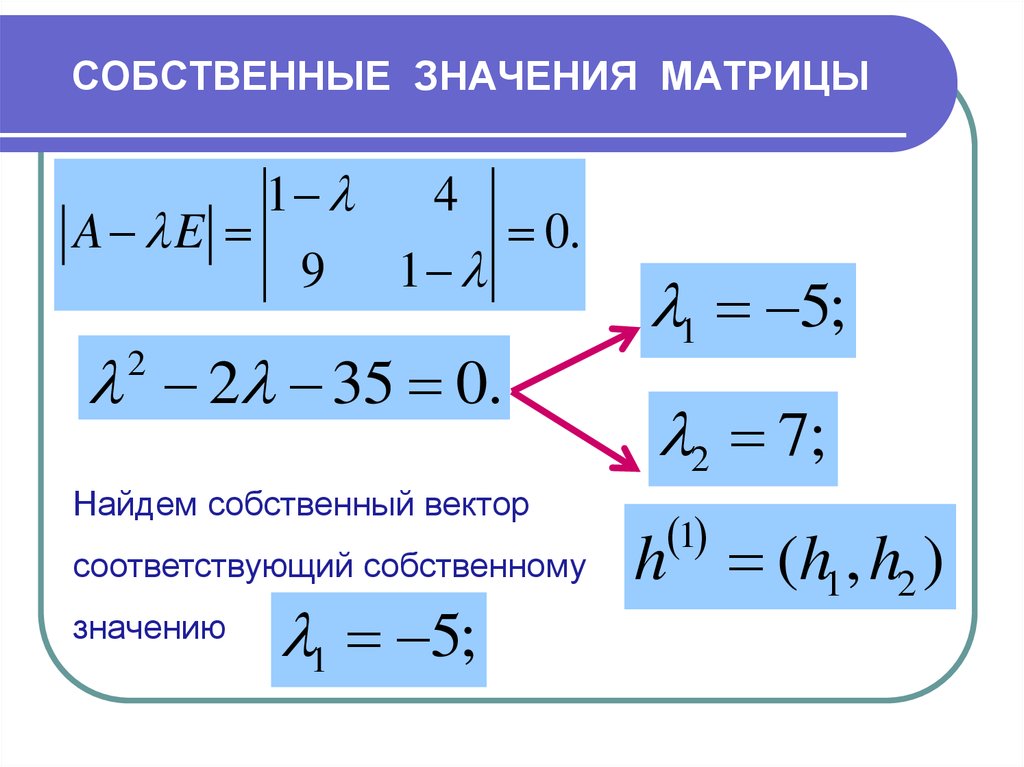
9. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
A E1
4
9
1
0.
2 35 0.
2
Найдем собственный вектор
соответствующий собственному
значению
1 5;
1 5;
2 7;
1
h (h1 , h2 )
10. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
h1 0( A E ) h 0, ( A E )
h2 0
4 h1 0 6 4 h1 0
1 ( 5)
h
h
1 ( 5) 2 0 9 6 2 0
9
6h1 4h2 0
h2 1,5h1.
9h1 6h2 0
Положив
h1 c1 ,
получим
h1 c1
; c1 0.
h2 1,5c1
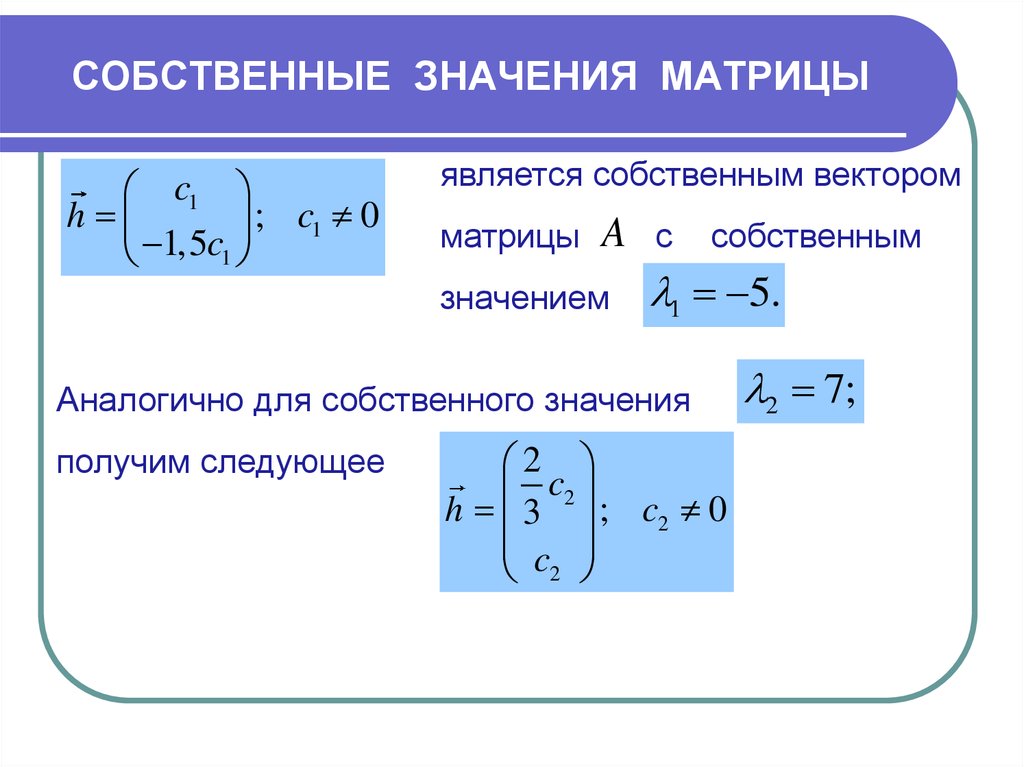
11. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
c1h
; c1 0
1,5c1
является собственным вектором
матрицы
A
значением
с
собственным
1 5.
Аналогично для собственного значения
получим следующее
2
c2
h 3
; c2 0
c2
2 7;
12. Свойства собственных значений матрицы
Произведение собственных значений матрицыравно ее определителю
A
A 1 2 ...... n
Число отличных от нуля собственных значений
матрицы
A
равно ее рангу.
Все собственные значения матрицы отличны от нуля
только и только тогда, когда матрица
невырожденная.
A
13. Свойства собственных значений матрицы
Если0
матрицы A
матрицы
Если
собственное значение невырожденной
1
, то
1
A
.
1
собственное значение
0 собственное значение матрицы A
собственное значение
m
натуральное число).
матрицы
Am
(m–
, то
14. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
,Если из характеристического уравнения
1.
(a11 )
a 21
a12
...
a1 n
(a 22 ) ...
a2 n
найдено собственное
1
a n1
an 2
... (a n n )
кратности k1 , 1 k1 n ,
то поиск соответствующих числу 1 собственных
векторов h 0 матрицы А сводится к решению
...
...
...
линейной системы
квадратной матрицей
...
0
значение
( A 1 E ) h 0 с постоянной
A 1 E
порядка
n.
15. Линейная зависимость векторов
Определение . Векторы a1 , a2 ,..., an линейноговекторного пространства V называются линейно
зависимыми, если существуют числа
1 , 2 ,... n , не все равные нулю, такие, что
справедливо равенство:
1a1 2 a2 .... n an 0 (1 )
Определение . Векторы a1 , a2 ,..., an
линейного
векторного пространства называются линейно
независимыми, если выполнение равенства (1)
возможно только при условии:
1 2 n 0
.
16. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Система( A 1 E ) h 0
всегда имеет бесконечное множество решений,
в котором число базисных (то есть максимальное число
линейно независимых) решений равно
где
r1
n r1 ,
ранг матрицы , то есть целое
неотрицательное число,
0 r1 n 1.
17. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Поэтому любому собственному значению квадратнойматрицы А соответствует хотя бы один линейно
независимый собственный вектор.
Более того, число линейно независимых собственных
векторов, отвечающих собственному значению
кратности
k1 ,
не превосходит числа
k1 .
1
18. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
2. Если1
простое собственное значение
матрицы A, тогда этому числу отвечает ровно
один линейно независимый собственный вектор
h1 0, который находим из системы ( A 1 E ) h 0,
например, с помощью метода Гаусса.
19. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
3. Случай, когда характеристическое уравнениеb1
n
n 1
b2
n 2
. . . bn 0
имеет комплексный корень
1
кратности k1 1.
Так как данное алгебраическое уравнение с
действительными коэффициентами, то оно обязательно
имеет корень
отношению к
.
2
1 .
комплексно–сопряженный по
20. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Кратность корня2
равна числу
k1.
следует найти собственные векторы ,
соответствующие собственному значению
Поэтому
1
.
Далее нужно построить к ним комплексно-сопряженные
векторы, которые являются собственными
векторами, соответствующими собственному
значению
2 .
21. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
4. Пусть у матрицы А есть кратное собственное.
значение 1 кратности k1 2Тогда,
решая систему
будет найдено n r1 линейно независимых собственных
векторов, отвечающих числу
1 .
Причем число n r1 удовлетворяет двойному
неравенству: 1 n r1 k1 ,
где r1 r( A 1E).
22. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Замечание. Если оказывается, что n r1 k1 , то длясобственного значения
1
будет найдено столько
линейно независимых собственных векторов, какова
кратность рассматриваемого собственного значения
1
23. Примеры
1. Найти собственные значения и собственныевекторы матрицы
4 1
.
A
1 2
Решение. Найдем собственные значения матрицы
A E
(4 )
1
1
(2 )
(4 ) (2 ) 1 2 6 9 0
( 3) 2 0.
24. Примеры
,.
1 3 собственное значение кратности
k1 2.
h1 0
( A E ) h 0, ( A E )
h2 0
1 h1 0
(4 3)
(2 3) h2 0
1
h1 h2 C
Ответ:
1
h1 .
1
1
h C
1
1 1 0 ( 1) 1 1 0
.
1 1 0
0 0 0






















 Математика
Математика








