Понятие первообразной. 11 класс

1. Понятие первообразной.

ПОНЯТИЕ
ПЕРВООБРАЗНОЙ.

2. Содержание

СОДЕРЖАНИЕ
понятие первообразной
неопределенный интеграл
таблица первообразных
три правила нахождения первообразных
определенный интеграл
вычисление определенного интеграла
площадь криволинейной трапеции
площадь криволинейной трапеции (1)
площадь криволинейной трапеции (2)
площадь криволинейной трапеции (3)
площадь криволинейной трапеции (4)
пример (1)
пример (2)

3.

4.

Как по скорости движения тела найти закон
его движения?

5.

6.

7.

8. Понятие первообразной

ПОНЯТИЕ ПЕРВООБРАЗНОЙ
Функцию F(x) называют первообразной для
функции f(x) на интервале (a; b), если на нем
производная функции F(x) равна f(x):
F ( x ) f ( x )
Операцию, обратную дифференцированию
называют интегрированием.

9.

Примеры
1. f(x) = 2x; F(x) = x2
F (x)= (x2) = 2x = f(x)
2. f(x) = – sin x; F(x) = сos x
F (x)= (cos x) = – sin x = f(x)
3. f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F (x)= (2x3 + 4x) = 6x2 + 4 = f(x)
4. f(x) = 1/cos2 x; F(x) = tg x
F (x)= (tg x) = 1/cos2 x= f(x)

10. Неопределенный интеграл

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенным интегралом от непрерывной
на интервале (a; b) функции f(x) называют
любую ее первообразную функцию.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).

11.

Примеры
1. Adx Ax C ; Ax C A
x
x
x
x
2. e dx e С; e C e
3. sin xdx cos x С ;
4
x
4. x dx
С;
4
3
cos x C
sin x
tg x C
1
2
cos x
x
1
С 4x 3 x 3
4
4
1
5.
dx tg x C ;
2
cos x
4

12.

Три правила нахождения
первообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf(х).
3º Если F(x) есть первообразная для f(x), а k и b –
1
постоянные, причем k ≠ 0, то функция
F(kx + b)
k
есть первообразная для f(kx + b).

13. Таблица первообразных

ТАБЛИЦА ПЕРВООБРАЗНЫХ
F(x)
x n 1
C
n 1
2x x
C
3
sin x C
cos x C
tgx C
ctgx C
f(x)
F(x)
f(x)
a C
ax
lna
1
C
x
ln x
cos x
ex C
sin x
1
сos 2 x
1
sin2 x
C
ex
Cx
loga x C
1
x lna
x
n
х
x
arcsin x C
1
1 x2

14.

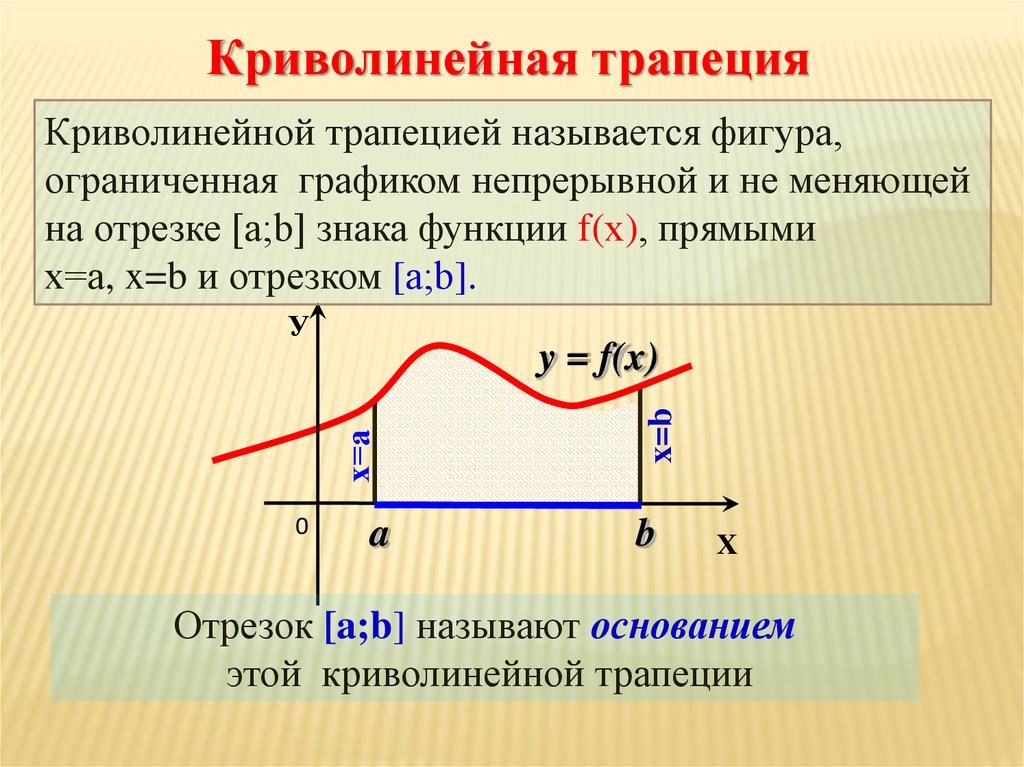
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции

15.

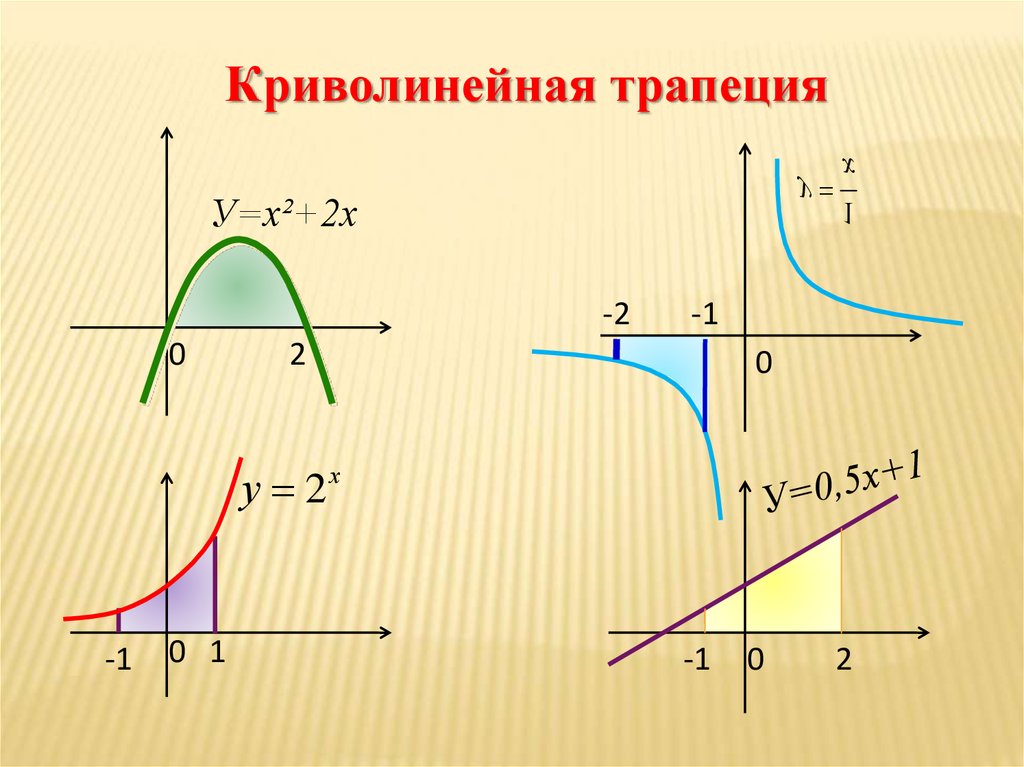
Криволинейная трапеция
х
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2

16.

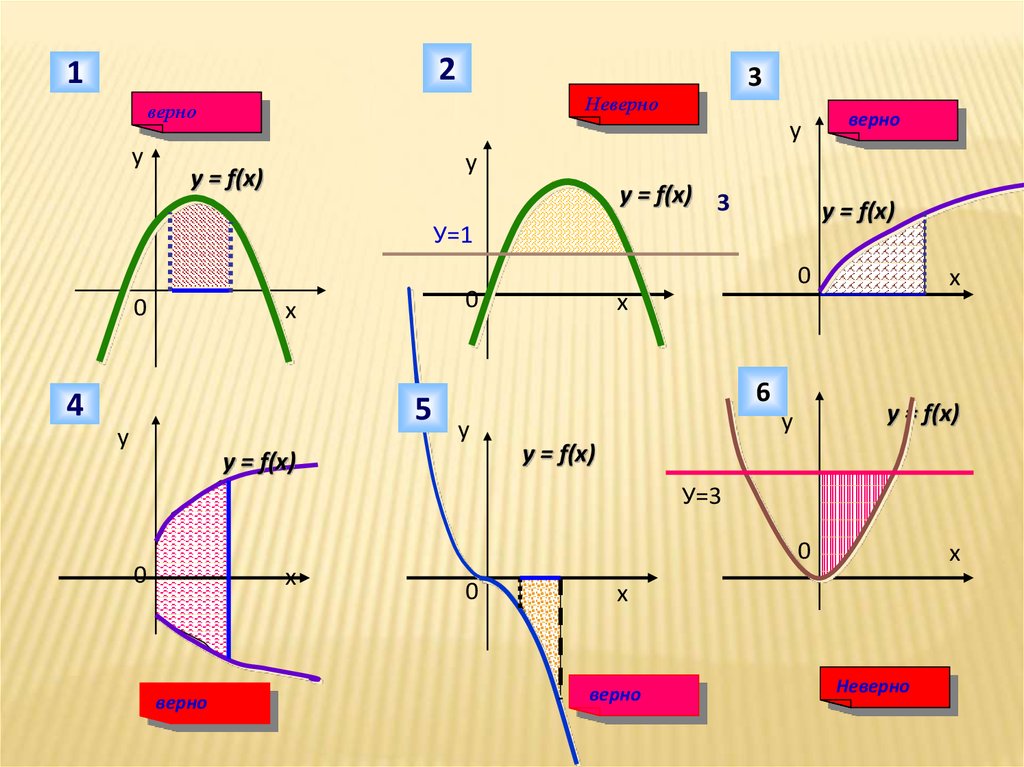
2
1
Неверно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
4
0
0
х
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
верно
0
х
х
верно
Неверно

17.

ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

18.

Площадь криволинейной трапеции.
y f (x)
y
S
0
a
b
x
S F (b) F (a)
где F(x) – любая первообразная функции f(x).

19.

Формула Ньютона-Лейбница
S F (b) F (a)
b
f ( x)dx F (b) F (a)
a
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716

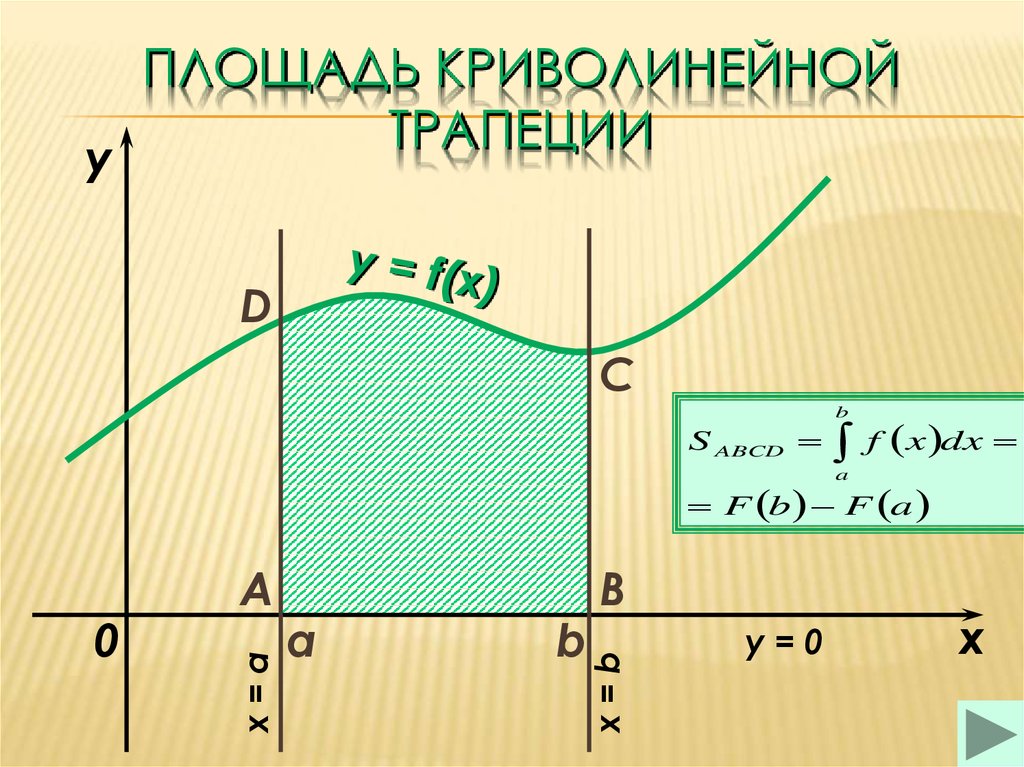
20. Площадь криволинейной трапеции

y
ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ
ТРАПЕЦИИ
D
C
b
S ABCD
f x dx
a
F b F a
a
b
B
x=b
x=a
0
A
y=0
x

21. Площадь криволинейной трапеции (1)

ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ
ТРАПЕЦИИ (1)
y
B
b
y=0
x
b
S ABCD f x dx
F a F b
D
C
x=b
a
x=a
0
A
a

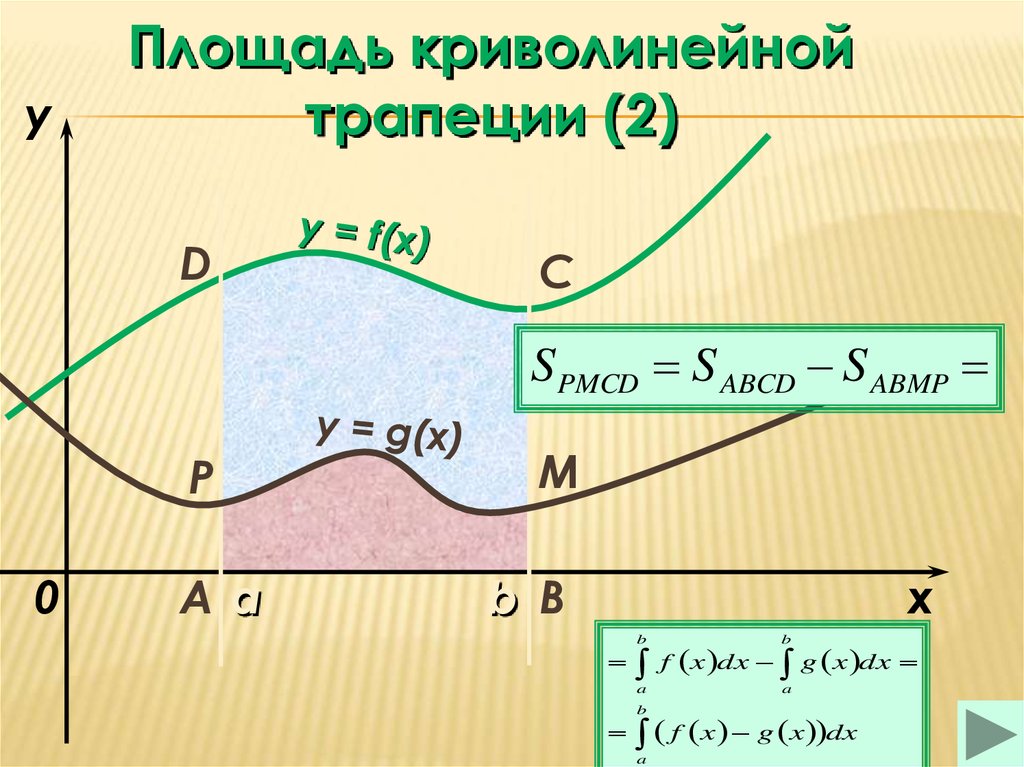
22.

y
Площадь криволинейной
трапеции (2)
D
C
S PMCD S ABCD S ABMP
P
0
Aa
M
b B
x
b
b
a
a
f x dx g x dx
b
f x g x dx
a

23.

y
Площадь криволинейной
трапеции (3)
D
0
A
a
C
S PMCD S ABCD S ABMP
B
b
x
P
M
b
b
a
a
f x dx g x dx
b
f x g x dx
a

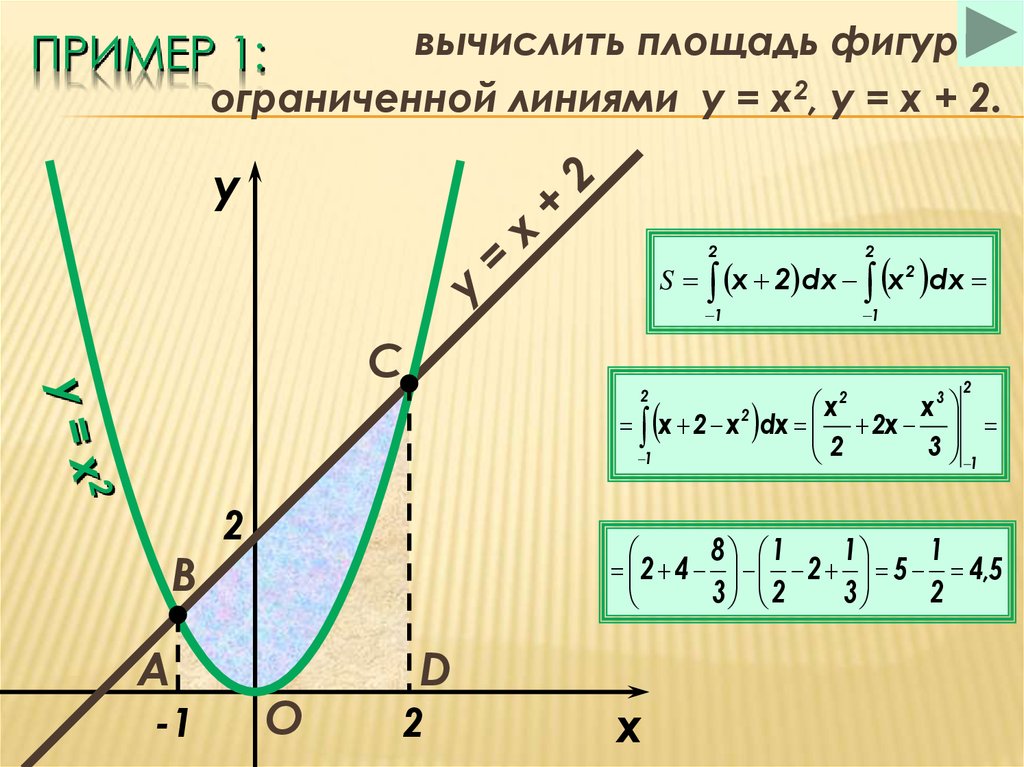
24. Пример 1:

вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
ПРИМЕР 1:
y
S
C
B
A
-1
2
2
2
1
1
2
x
2
dx
x
dx
2
2
3
x
x
2
х 2 х dx 2x
3 1
2
1
2
8 1
1
1
2 4 2 5 4,5
3 2
3
2
O
D
2
x

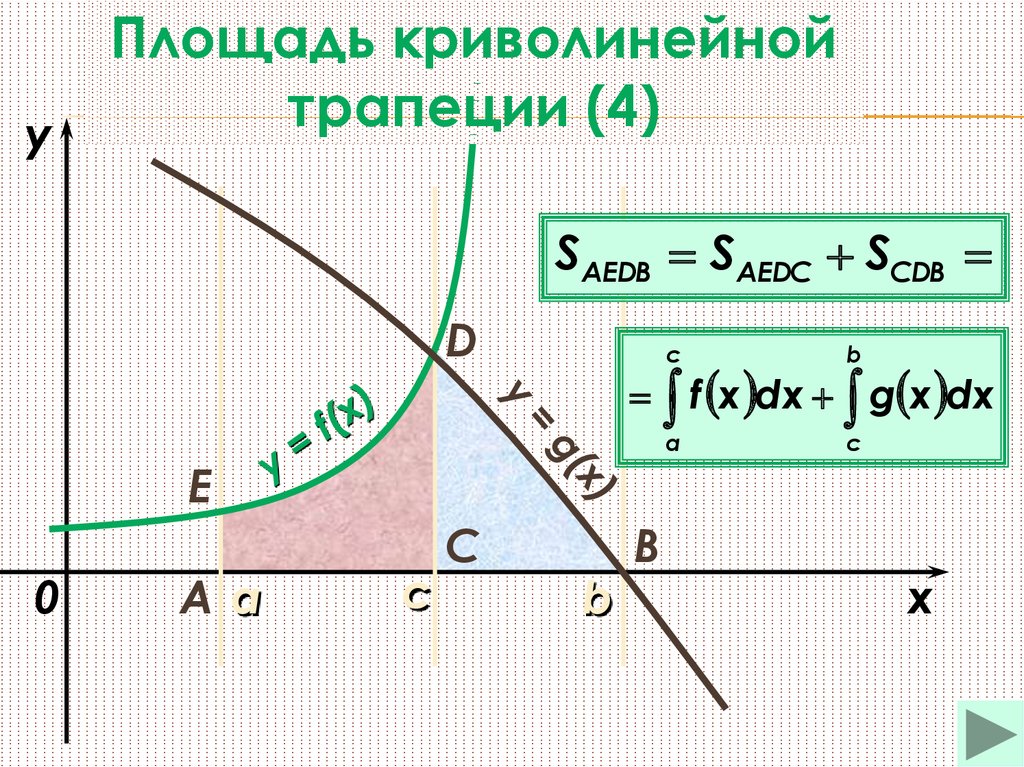
25.

y
Площадь криволинейной
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x

26.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x

27.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
8
x - 2 dx 2
2
2
4
3 4
x 2
8 - хdx
3
4 8 x 8 x
3
2
8
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3

28. Определенный интеграл

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
b
f x dx F x
b
a
F b F a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен
площади
криволинейной
трапеции,
образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

29. Вычисление определенного интеграла

ВЫЧИСЛЕНИЕ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
3x
2
2
2 x 1 dx x x x
3
2
2
1
1
2 2 2 1 1 1 6 1 5
10
3
3
2
3
2
2 x 6 x 6
x 6 dx
3
10
3
2 10 6 10 6 2 3 6 3 6 80
2
18 7
3
3
3
3