Статистическое описание равновесных состояний. Функция распределения. Принцип детального равновесия. Распределение Максвелла

1. Лекция 15-2020 г.

1. Статистическое описание равновесных состояний
Функция распределения.
2. Принцип детального равновесия. Распределение
Максвелла. Экспериментальная проверка
распределения Максвелла.
3. Барометрическая формула. Распределение
Больцмана.
4. Фазовое пространство. Распределение МаксвеллаБольцмана.
5. Равновесные флуктуации. Статистическое
обоснование второго начала термодинамики.
Формула Больцмана для статистической энтропии.

2.

Статистическое описание равновесных
состояний
Статистический метод — это вероятностный метод
исследования систем из большого числа частиц. Данный
метод оперирует статистическими закономерностями
и средними (усредненными) значениями физических величин,
которые характеризуют всю систему.
Этот метод лежит в основе молекулярной физики — раздела
физики, изучающего строение и свойства вещества исходя из
молекулярно-кинетических представлений, основывающихся
на том, что все тела состоят из атомов, молекул или ионов
находящихся в непрерывном хаотическом движении.
А.С. Чуев, 2020
2

3.

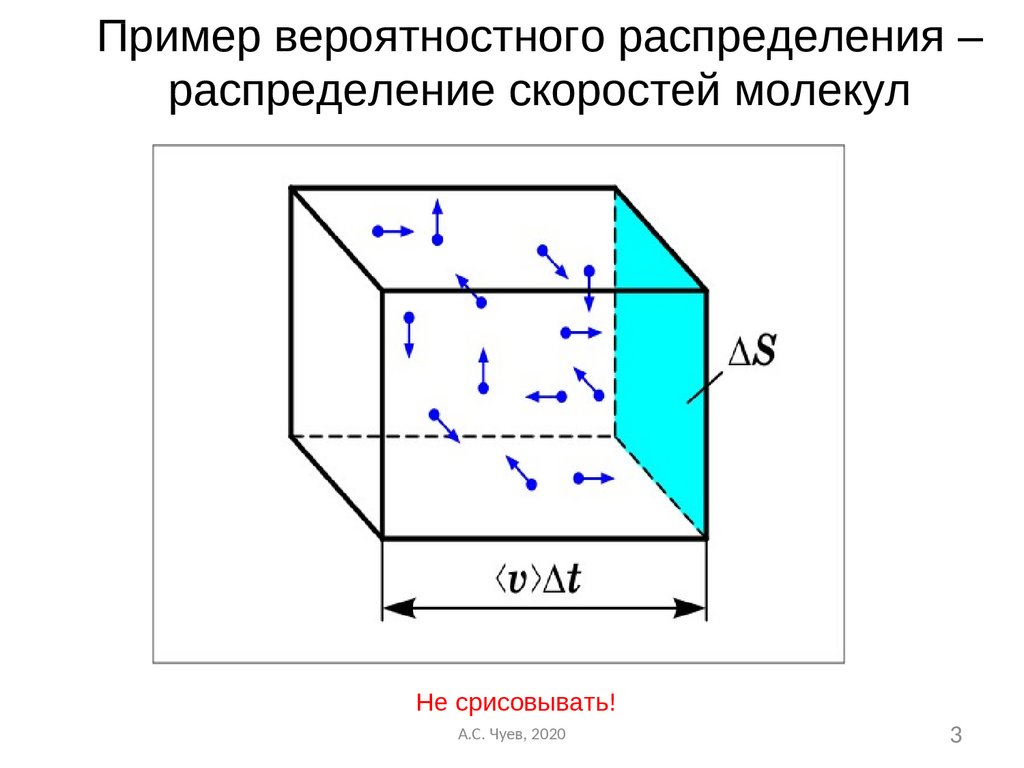
Пример вероятностного распределения –
распределение скоростей молекул
Не срисовывать!
А.С. Чуев, 2020
3

4. Математическое определение вероятности: вероятность какого-либо события – это предел, к которому стремится отношение числа

случаев,
приводящих к осуществлению события, к общему
числу случаев, при бесконечном увеличении
последних:
n
P lim
n n
Здесь n число раз, когда событие произошло, а
n общее число опытов. Отсюда следует, что Р
может принимать значения от нуля до единицы.
А.С. Чуев, 2020
4

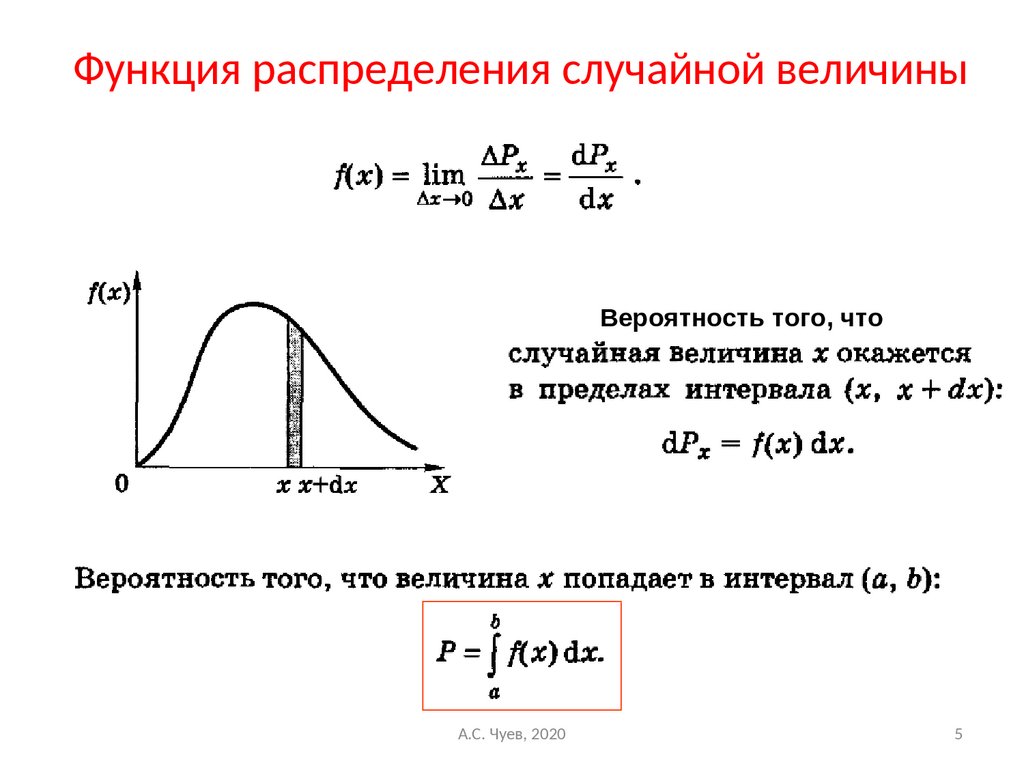
5. Функция распределения случайной величины

Вероятность того, что
А.С. Чуев, 2020
5

6.

Для распределения молекул газа по скоростям:
А.С. Чуев, 2020
6

7.

Плотность распределения молекул по скоростям по
одной координате
Условие нормировки:
В среднем значения скорости нулевые из-за равновероятности их
направлений
Общая плотность распределения
А.С. Чуев, 2020
7

8.

Общая формула функции распределения скоростей по одной оси
α x2
х А exp
2
Вид функции после
нормировки:
С учетом:
А.С. Чуев, 2020
8

9. Функция распределения Максвелла по модулю скорости

А.С. Чуев, 2020
9

10.

А.С. Чуев, 2020
10

11.

А.С. Чуев, 2020
11

12.

Из
С учетом
Получаем закон распределения Максвелла по модулю
скорости
А.С. Чуев, 2020
12

13.

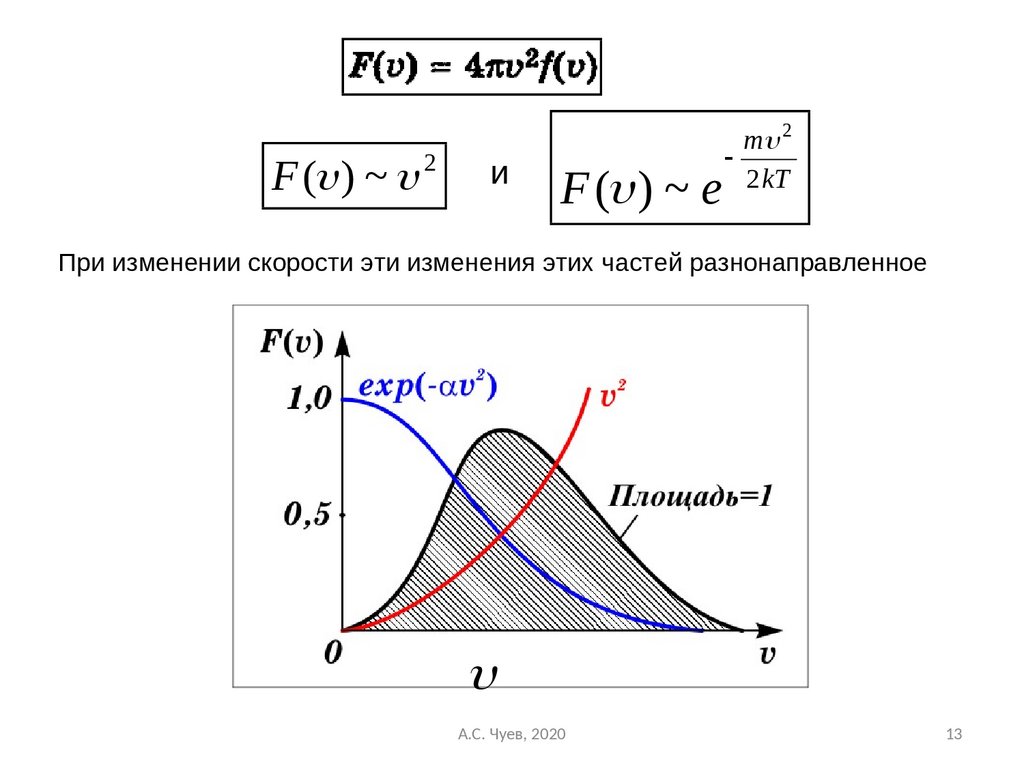
F ( ) ~ 2
и
F ( ) ~ e
m 2
2 kT
При изменении скорости эти изменения этих частей разнонаправленное
А.С. Чуев, 2020
13

14.

Данную функцию можно представить в виде:
2
F (υ) Aυ e
А.С. Чуев, 2020
mυ 2
2 kT
.
14

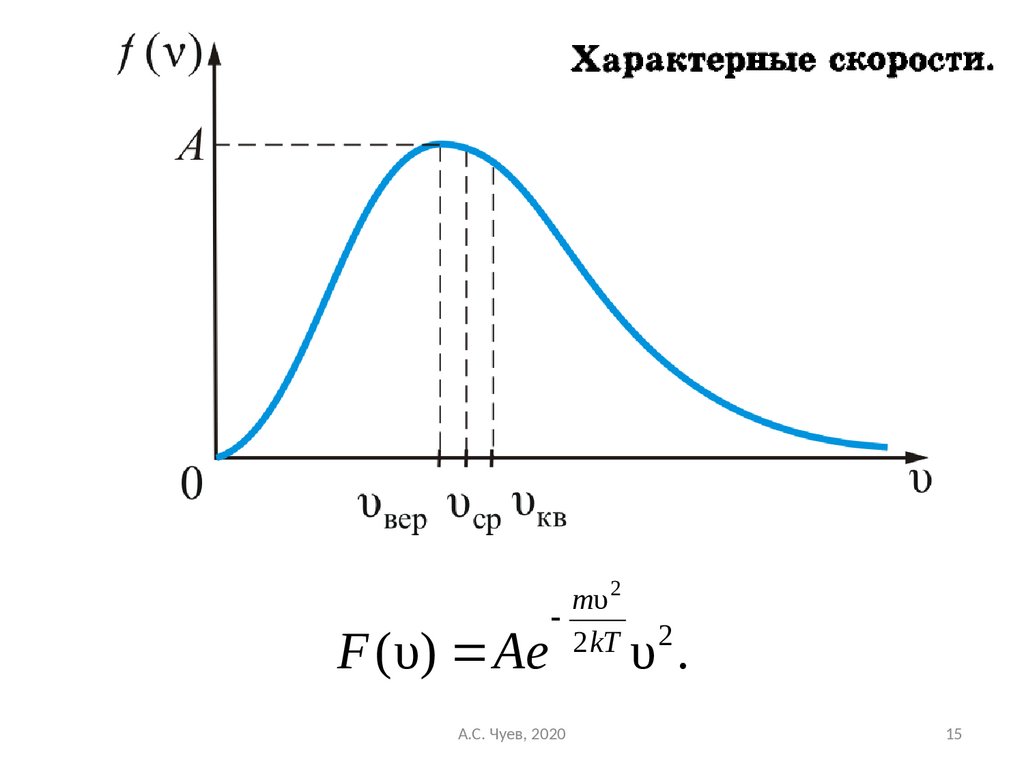
15.

F ( υ) Ae
mυ 2
2 kT
А.С. Чуев, 2020
2
υ.
15

16.

Факультативно
(Из Савельева)
Определение средних
значений через
плотности
распределения
А.С. Чуев, 2020
16

17.

А.С. Чуев, 2020
17

18. Выводы из формулы: - Вид распределения молекул газа по скоростям, для каждого газа зависит от рода газа (m) и от температуры

Выводы из формулы:
F ( υ) Ae
mυ 2
2 kT
2
υ.
- Вид распределения молекул газа по скоростям,
для каждого газа зависит от рода газа (m) и от
температуры (Т). Давление P и объём газа V на
распределение молекул не влияют.
- В показателе степени стоит отношение,
кинетической энергии, соответствующей данной
скорости υ к средней энергии теплового движения
молекул при данной температуре: mυ 2
2kT
А.С. Чуев, 2020
18

19. Доска Гальтона

А.С. Чуев, 2020
19

20. Формула Максвелла для относительных скоростей

Для решения многих задач удобно
использовать формулу Максвелла, где скорость
выражена в относительных единицах.
Относительную скорость обозначим через u:
υ где
u
,
υвер
υ вер
А.С. Чуев, 2020
2kT
m
20

21. В таком виде функция распределения не зависит ни от рода газа, ни от температуры

4 2 u
F (u ) u e
2
Формула Максвелла для относительных скоростей
В таком виде функция распределения не
зависит ни от рода газа, ни от температуры
А.С. Чуев, 2020
21

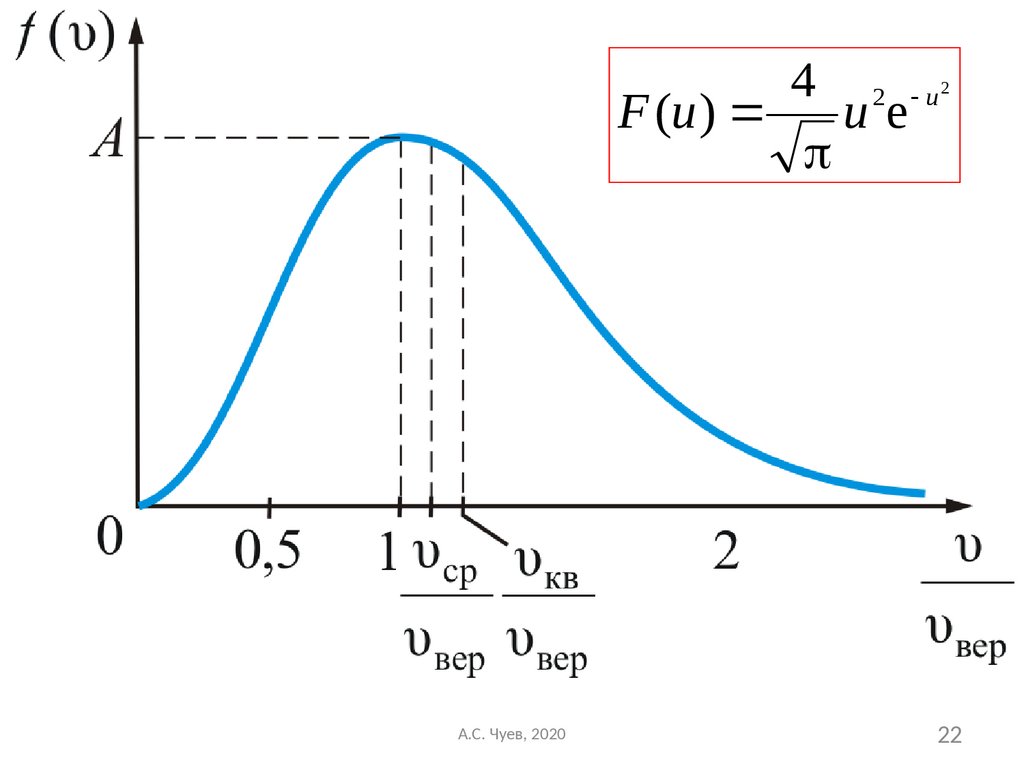
22.

4 2 u
F (u ) u e
А.С. Чуев, 2020
2
22

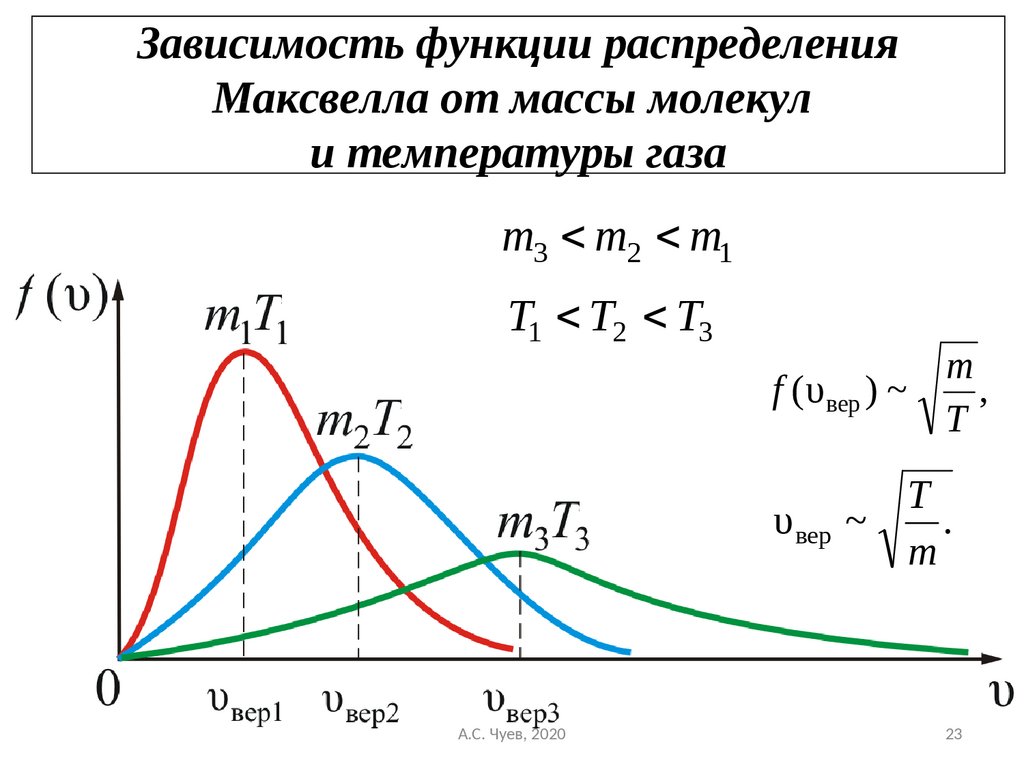
23. Зависимость функции распределения Максвелла от массы молекул и температуры газа

m3 m2 m1
T1 T2 T3
m
f ( υ вер ) ~
,
T
υ вер ~
А.С. Чуев, 2020
T
.
m
23

24. Распределение Больцмана для идеального газа во внешнем потенциальном поле. Барометрическая формула

А.С. Чуев, 2020
24

25. Барометрическая формула

Рассмотрим ещё один, очень важный закон.
Атмосферное давление на какой-либо
высоте h обусловлено весом выше
лежащих слоёв газа.
Пусть P – давление на высоте h, а
P ΔP – на высоте h Δh
А.С. Чуев, 2020
25

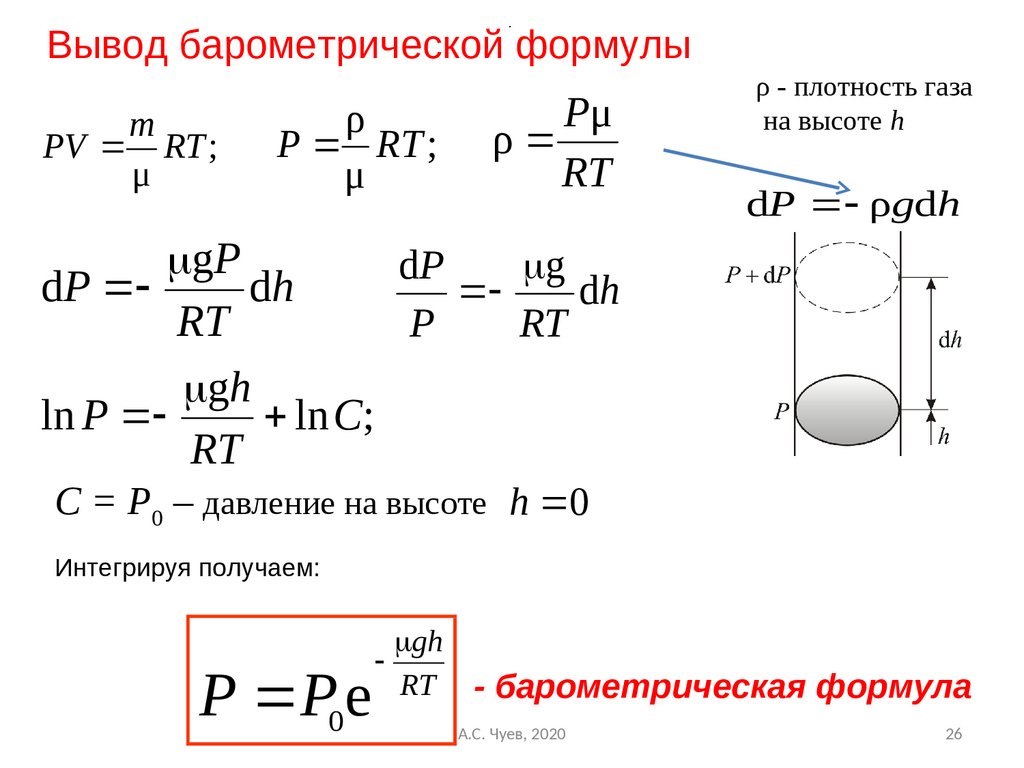
26.

.
Вывод барометрической формулы
m
PV RT ;
μ
ρ
P RT ;
μ
Pμ
ρ
RT
ρ - плотность газа
на высоте h
dP ρgdh
gP
dP
g
dP
dh
dh
RT
P
RT
gh
ln P
ln C;
RT
С = Р0 – давление на высоте h 0
Интегрируя получаем:
P P0e
gh
RT - барометрическая формула
А.С. Чуев, 2020
26

27. Из барометрической формулы следует, что P убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура

(например, на больших высотах концентрация
легких газов Не и Н2 гораздо больше чем у
поверхности Земли).
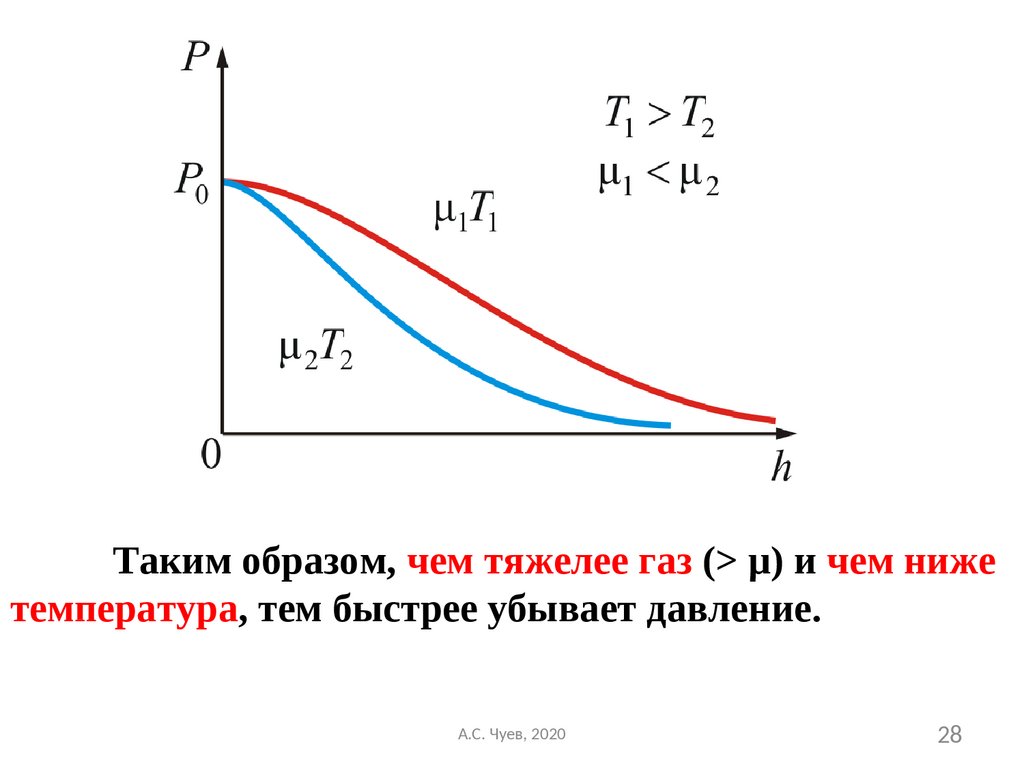
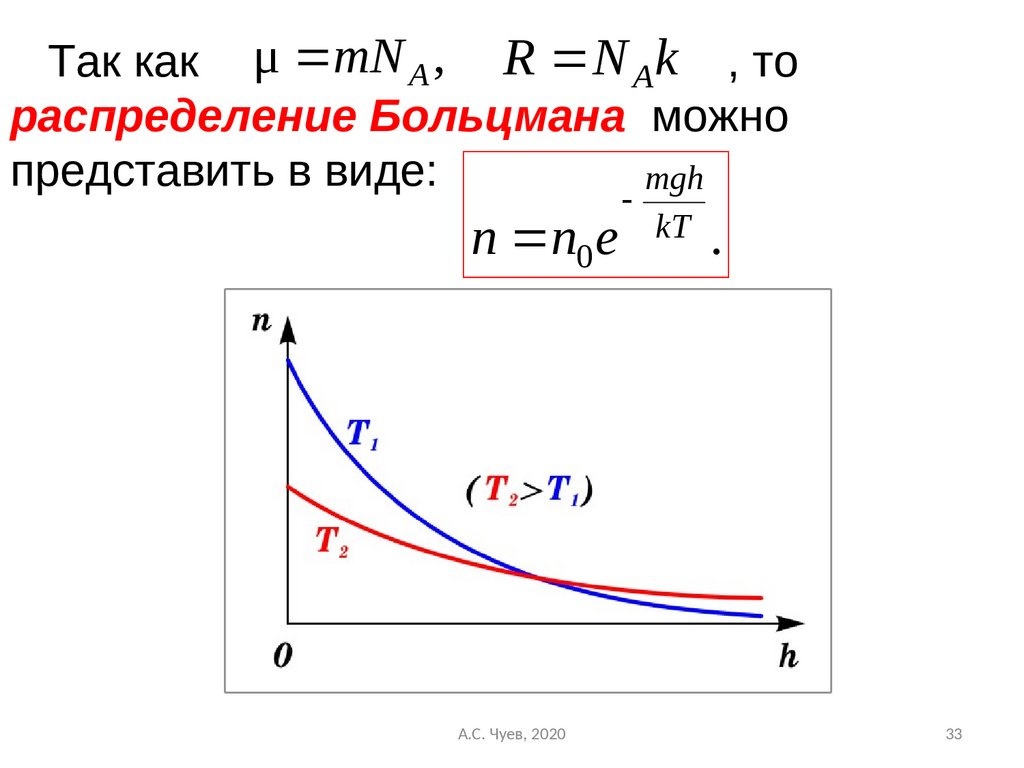
На след. Рисунке изображены две кривые,
которые можно трактовать, либо как
соответствующие разным μ (при одинаковой Т),
либо как отвечающие разным Т, при одинаковых
μ.
А.С. Чуев, 2020
27

28.

Таким образом, чем тяжелее газ (> μ) и чем ниже
температура, тем быстрее убывает давление.
А.С. Чуев, 2020
28

29. Распределение Больцмана

Распределение Больцмана определяет
распределение частиц в силовом поле в
условиях теплового равновесия.
А.С. Чуев, 2020
29

30. Пусть идеальный газ находится в поле консервативных сил, в условиях теплового равновесия. При этом, концентрация газа будет

различной в точках с различной потенциальной
энергией, что необходимо для соблюдения
условий механического равновесия.
Число молекул в единичном объеме n убывает с
удалением от поверхности Земли, и давление, в
силу соотношения P nkT
тоже убывает.
А.С. Чуев, 2020
30

31. Исходя из основного уравнения молекулярно-кинетической теории: , заменим P и P0 в барометрической формуле на n и n0 и получим

Исходя из основного уравнения
молекулярно-кинетической теории: P nkT ,
заменим P и P0 в барометрической формуле
на n и n0 и получим распределение
Больцмана для молярной массы газа:
n n0
μgh
RT
e
,
где n0 и n число молекул в единичном
объёме на высоте h = 0 и h, соответственно.
А.С. Чуев, 2020
31

32.

А.С. Чуев, 2020
32

33.

Так как μ mN A , R N Ak , то
распределение Больцмана можно
представить в виде:
mgh
n n0 e
А.С. Чуев, 2020
kT
.
33

34. Так как –потенциальная энергия, следовательно, распределение Больцмана характеризует распределение частиц по значениям

Так как U mgh –потенциальная энергия,
следовательно, распределение Больцмана
характеризует распределение частиц по
значениям потенциальной энергии:
n n0
U
kT
e
– это закон распределения частиц по
потенциальным энергиям – распределение
Больцмана.
Здесь n0 – число молекул в
единице объёма. Там, где U 0.
А.С. Чуев, 2020
34

35. Больцман доказал, что это соотношение справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном

Еще одна запись распределения Больцмана:
n1
e
n2
U1 U 2
kТ
Больцман доказал, что это соотношение справедливо
не только в потенциальном поле сил гравитации, но и в
любом потенциальном поле, для совокупности любых
одинаковых частиц, находящихся в состоянии
хаотического теплового движения.
А.С. Чуев, 2020
35

36. Закон распределения Максвелла-Больцмана

Закон распределения МаксвеллаБольцмана
А.С. Чуев, 2020
36

37.

А.С. Чуев, 2020
37

38.

А.С. Чуев, 2020
38

39. Закон Максвелла-Больцмана в представлении через потенциальную и кинетическую энергии, имеет вид:

dnU , K n 0
4
3/2
U K
m
2
kT
e
d .
2kT
А.С. Чуев, 2020
39

40. Закон распределения Максвелла-Больцмана в иной форме записи Здесь n0 – число молекул в единице объёма в той точке, где ; .

Закон распределения Максвелла-Больцмана в
иной форме записи
2
E
kT
dn n0 A e d .
Здесь E U K
n0 – число молекул в единице объёма в той точке,
где U 0 ;
m
A
2 kT
А.С. Чуев, 2020
3/2
.
40

41.

Понятие о фазовом пространстве
А.С. Чуев, 2020
41

42.

Двумерное фазовое пространство
Квантом двумерного фазового пространства является постоянная Планка.
А.С. Чуев, 2020
42

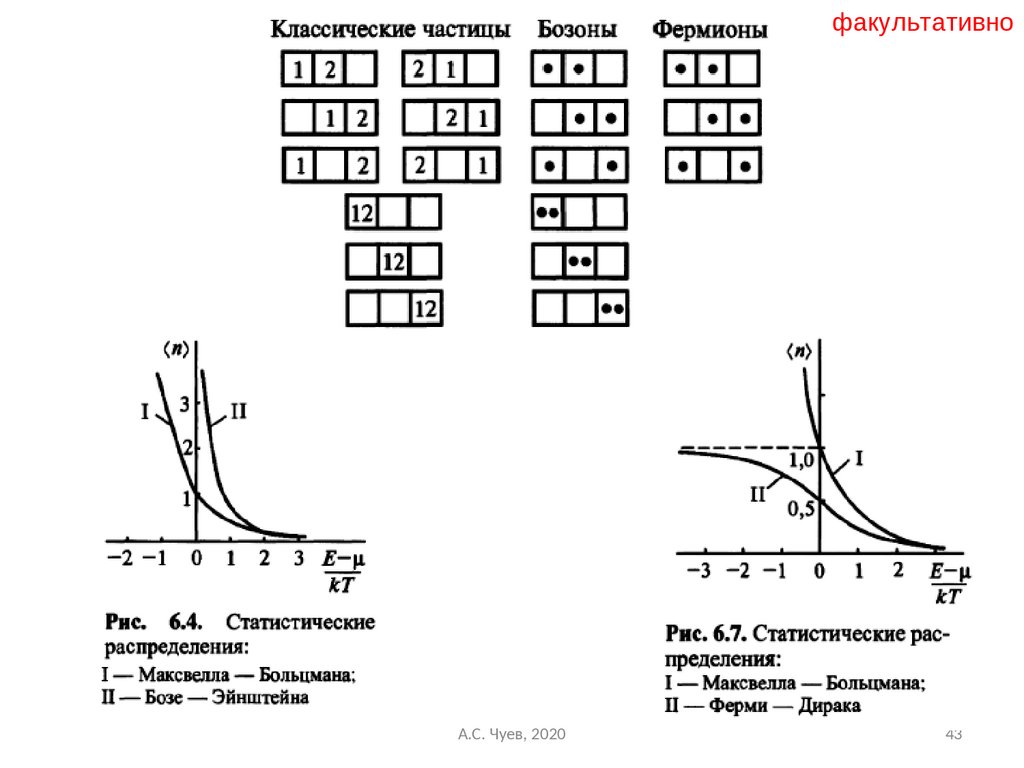
43.

факультативно
А.С. Чуев, 2020
43

44.

Понятие о фазовом пространстве,
распределения бозонов и фермионов
А.С. Чуев, 2020
факультативно
44

45. Статистический смысл энтропии

Различают понятия микро- и макросостояние
термодинамической системы
А.С. Чуев, 2020
45

46. Макросостояние – это состояние вещества, характеризуемое его термодинамическими параметрами. Состояние системы, характеризуемое

состоянием каждой входящей в систему
молекулы, называют микросостоянием.
Так как молекулы движутся хаотически, то
имеется много микросостояний, соответствующих
одному макросостоянию.
Обозначим W число микросостояний
соответствующее данному макросостоянию
(как правило W >> 1).
А.С. Чуев, 2020
46

47. Термодинамической вероятностью или статистическим весом макросостояния W  называется число микросостояний, осуществляющих

Термодинамической вероятностью или
статистическим весом макросостояния W
называется
число
микросостояний,
осуществляющих данное макросостояние (или
число перестановок одноименных элементов, при
которых сохраняется данное макросостояние).
Термодинамическая вероятность W
максимальна, когда система находится в
равновесном состоянии.
А.С. Чуев, 2020
47

48. В состоянии равновесия в термодинамике и вероятность максимальна и энтропия максимальна. Из этого можно сделать вывод, что

между
ними существует связь.
Но! Энтропия S – аддитивная величина:
т.е. она равна сумме энтропий тел, входящих в
систему.
n
S Si
i 1
А.С. Чуев, 2020
48

49. Вероятность сложного события, есть произведение вероятностей где W1 – первое состояние; W2 – второе состояние. Аддитивной

Вероятность сложного события, есть
произведение вероятностей
W W1W2
где W1 – первое состояние; W2 – второе
состояние.
Аддитивной величиной является
логарифм W:
n
ln W ln W1 ln W2 ... ln Wi
i 1
А.С. Чуев, 2020
49

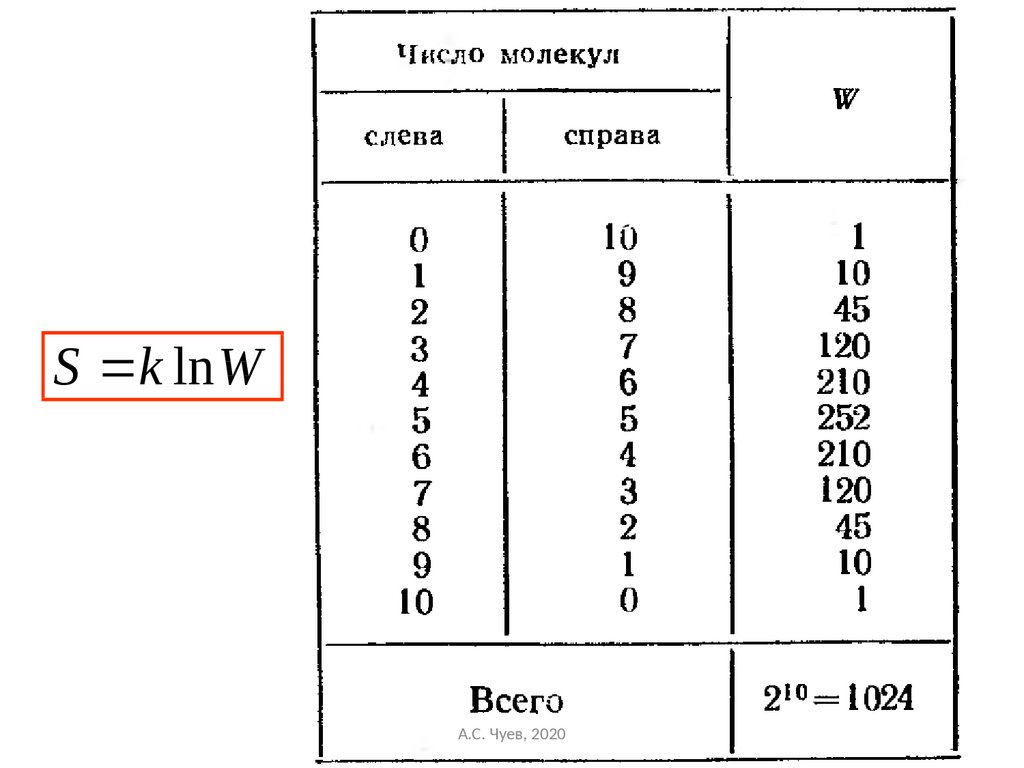
50. Больцман предложил, что энтропия где k – коэффициент (постоянная) Больцмана. С этой точки зрения энтропия выступает, как мера

Формула Больцмана для статистической
энтропии
Больцман предложил, что энтропия
S k ln W
где k – коэффициент (постоянная) Больцмана.
С этой точки зрения энтропия выступает,
как мера беспорядочности, хаотичности
состояния.
А.С. Чуев, 2020
50

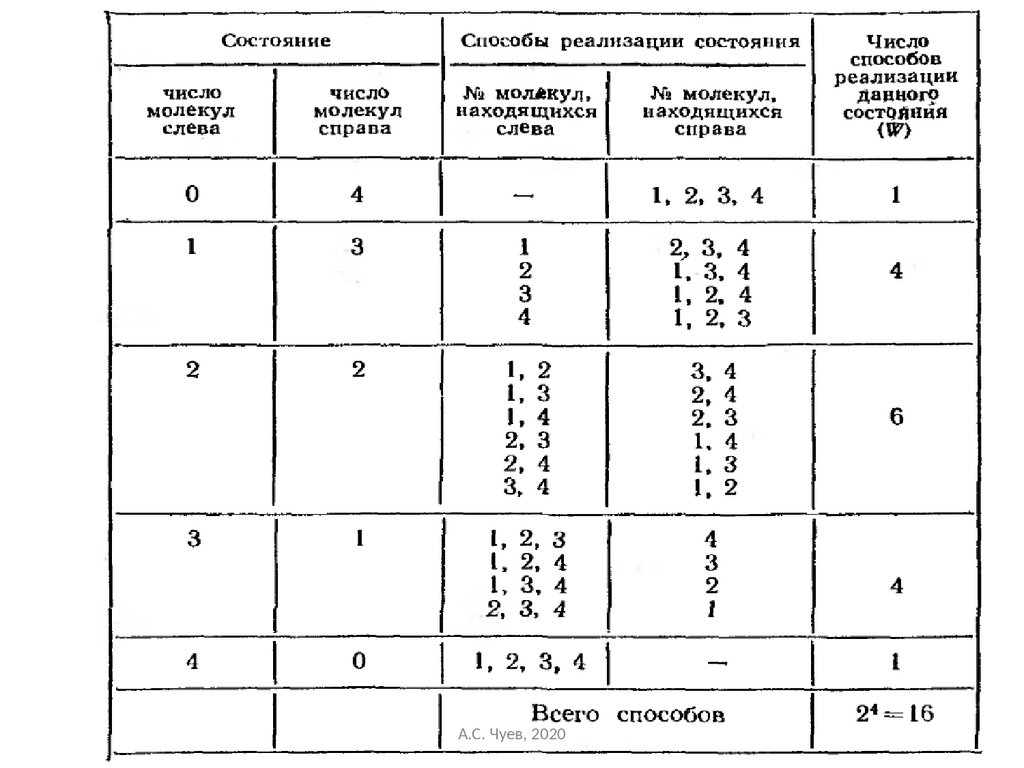
51.

Статистический вес и
термодинамическая вероятность
Число состояний
W
n – число частиц слева
(N - n ) – число частиц справа
Максимум числа состоянийА.С.
при
равномерном распределении
Чуев, 2020
51

52.

А.С. Чуев, 2020
52

53.

S k ln W
А.С. Чуев, 2020
53

54.

Конец лекции 15
А.С. Чуев, 2020
54