Похожие презентации:
Тригонометрические функции числового аргумента
1.
Тригонометрическиефункции числового
аргумента
2.
Тригонометрические формулыsin 1 cos
2
sin cos 1
2
2
2
cos 1 sin
2
2
sin 1 cos
2
cos 1 sin
2
3.
sintg
cos
cos
ctg
sin
1
tg
ctg
sin cos
tg ctg
1
cos sin
tg ctg 1
1
ctg
tg
4.
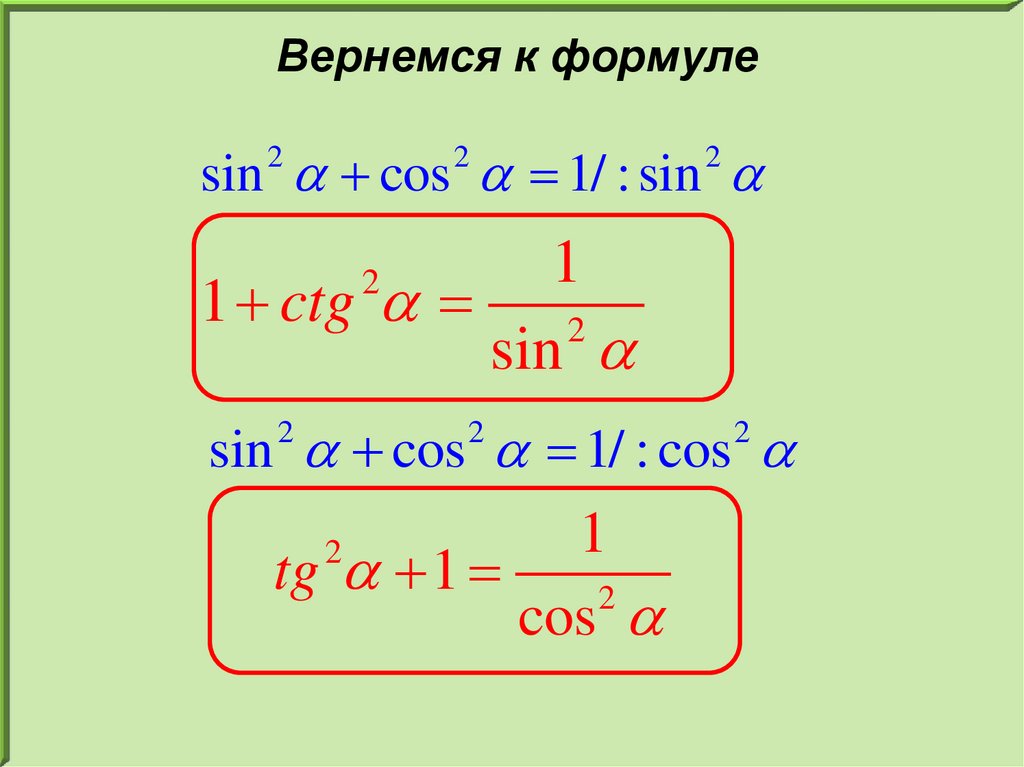
Вернемся к формулеsin cos 1/ : sin
2
2
2
1
1 ctg
2
sin
2
sin cos 1/ : cos
2
2
1
tg 1
2
cos
2
2
5.
1ctg
1
2
sin
2
1
1 ctg
2
sin
2
1
ctg
1
2
sin
1
sin
2
1 ctg
2
1
sin
2
1 ctg
6.
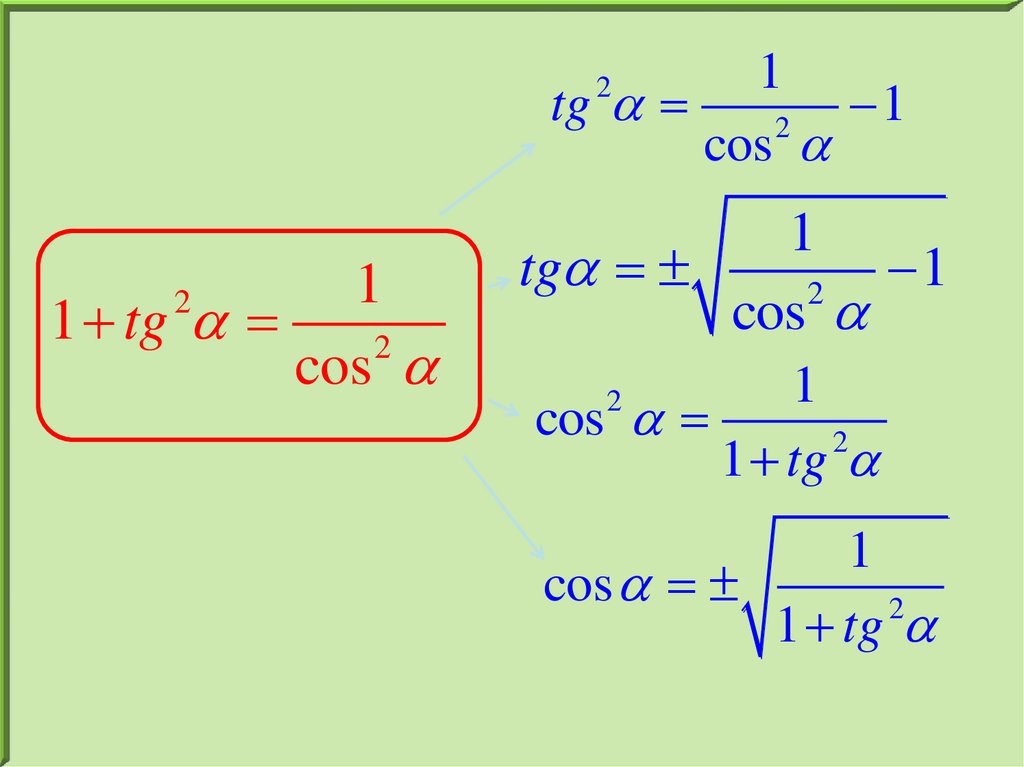
1tg
1
2
cos
2
1
1 tg
2
cos
2
1
tg
1
2
cos
1
cos
2
1 tg
2
1
cos
2
1 tg
7.
51) Дано : sin ,
( IIчетв.)
13
2
Найти : cos , tg , ctg
Решение :
cos 1 sin
2
25
144
12
1
169
169
13
sin
5
12
5
13
5
tg
: ( )
cos 13
13
12
13 12
12
1
ctg
=5
tg
12
5
12
Ответ : cos , tg , ctg
13
12
5
8.
2) Дано : tg 2,0
Найти : sin , cos , ctg
2
( Iчетв.)
Решение :
1
1
ctg
tg
2
1
1
1
1
cos
2
1 tg
1 4
5
5
1
2
sin 1 cos 1 4 2
5
5
5
1
1
2
Ответ : ctg , cos
, sin
2
5
5
9.
3)Упростите выражение :2
cos
2
2
2
2
а)ctg (cos 1) 2 ( sin ) cos
sin
sin
1 cos sin 2 (1 cos )2
б)
1 cos
sin
sin (1 cos )
2 2 cos
sin 1 2cos cos
sin (1 cos )
sin (1 cos )
2(1 cos )
2
sin (1 cos ) sin
2
2
10.
4) Докажите тождество :tg t sin t tg t sin t
2
2
2
2
Рассмотрим левую часть
2
2
2
2
2
sin
t
sin
t
sin
t
sin
t
cos
t
tg t sin t 2
2
cos t
1
cos t
2
2
sin t (1 cos t ) tg 2t sin 2 t
2
cos t
2
2
tg t sin t tg t sin t
2
2
2
2
Вывод : Тождество доказано.
11.
Формулы приведенияЭто формулы позволяющие
выражать значения
тригонометрических функций
любого угла через функции угла
первой четверти,
т. е. < 90
Например : sin( ), cos(2 )...
2
Всего из 32. Применяется следующее правило
12.
Мнемоническое правилоДостаточно задать себе два вопроса:
1. Меняется ли функция на кофункцию?
Ответ. Если в формуле присутствуют углы
вертикальной оси - 90° (π/2) или 270° (3π/2),
киваем головой по вертикали и сами себе
отвечаем: «Да»,
если же присутствуют углы горизонтальной оси
0° (π) или 360° (2π), то киваем головой
по горизонтали и получаем ответ: «Нет».
13.
2. Какой знак надо поставить в правой частиформулы?
Ответ. Знак определяем по левой части.
Смотрим, в какую четверть попадает данный
угол, и вспоминаем, какой знак в этой четверти
имеет функция, стоящая в левой части.
14.
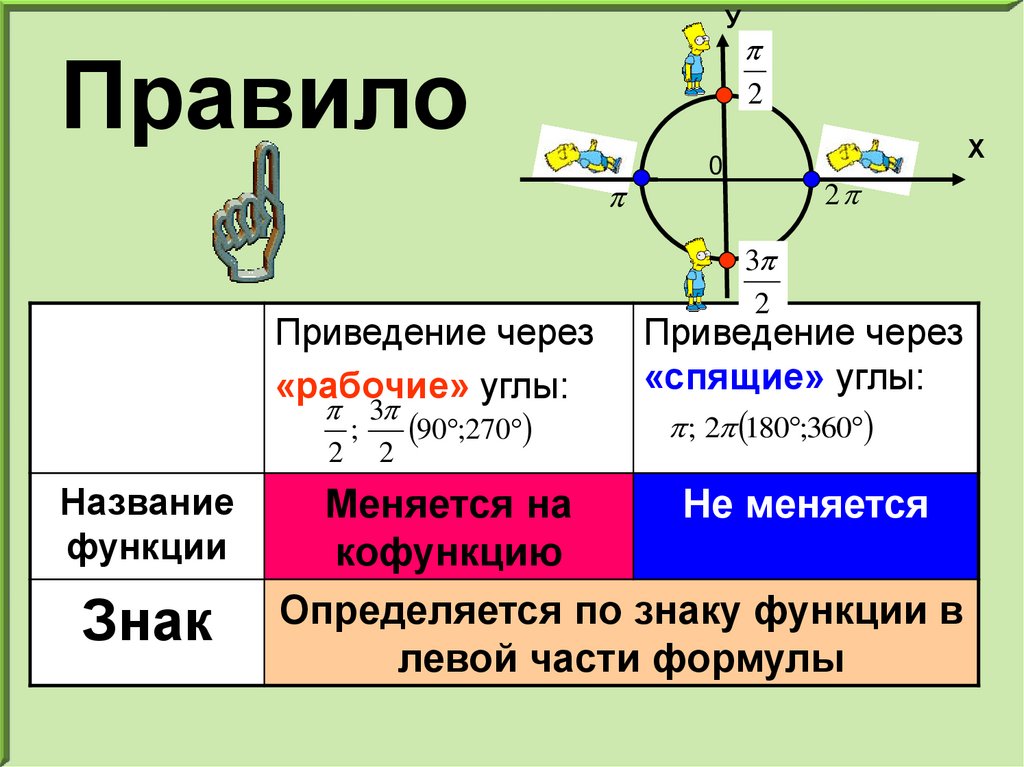
УПравило
Приведение через
«рабочие» углы:
3
2
Название
функции
Знак
;
2
90 ;270
2
Х
0
2
3
2
Приведение через
«спящие» углы:
; 2 180 ;360
Меняется на
Не меняется
кофункцию
Определяется по знаку функции в
левой части формулы
15.
sin 2 sinsin cos
2
tg tg
3
cos
sin
2
ctg 2 ctg
cos 180 cos
tg 270 0 ctg
0
16.
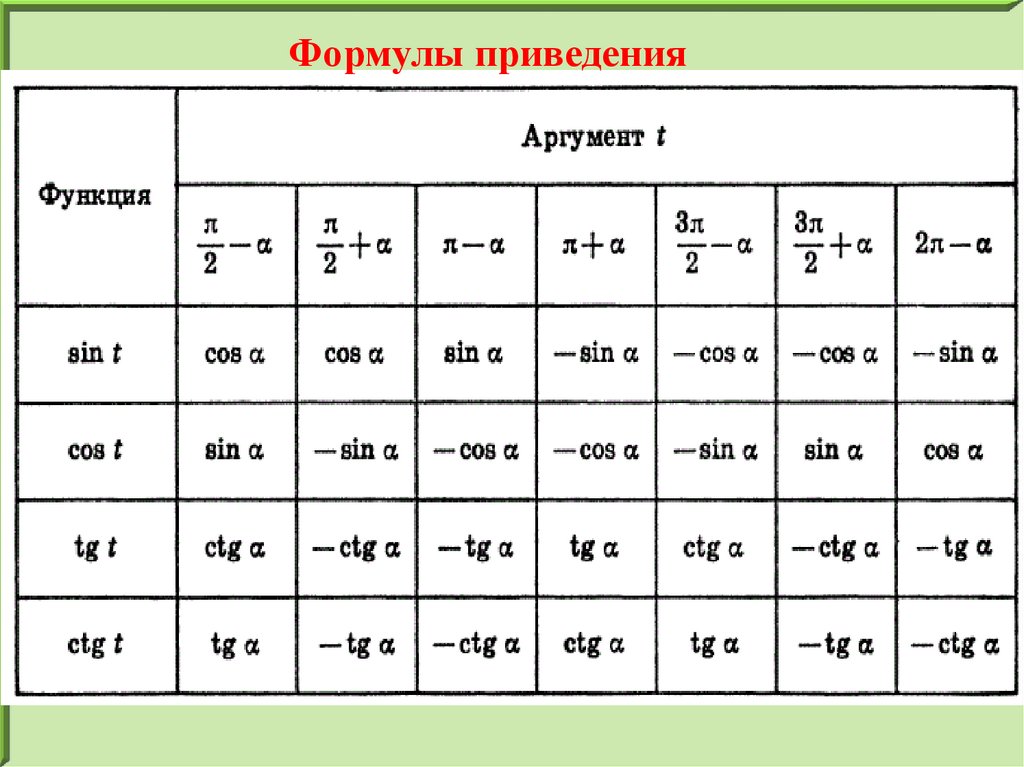
Формулы приведения17.
Например :8
2
1
1) cos
cos 2 cos(3 ) cos
3
3
3
3
2
2) sin( 585 ) sin(360 225 ) sin 225
sin(180 45 ) sin 45
3)tg 45 tg 0
5
1
4) ctg( ) ctg (1 ) ctg ( )
4
4
4
ctg
4
1
2
2
18.
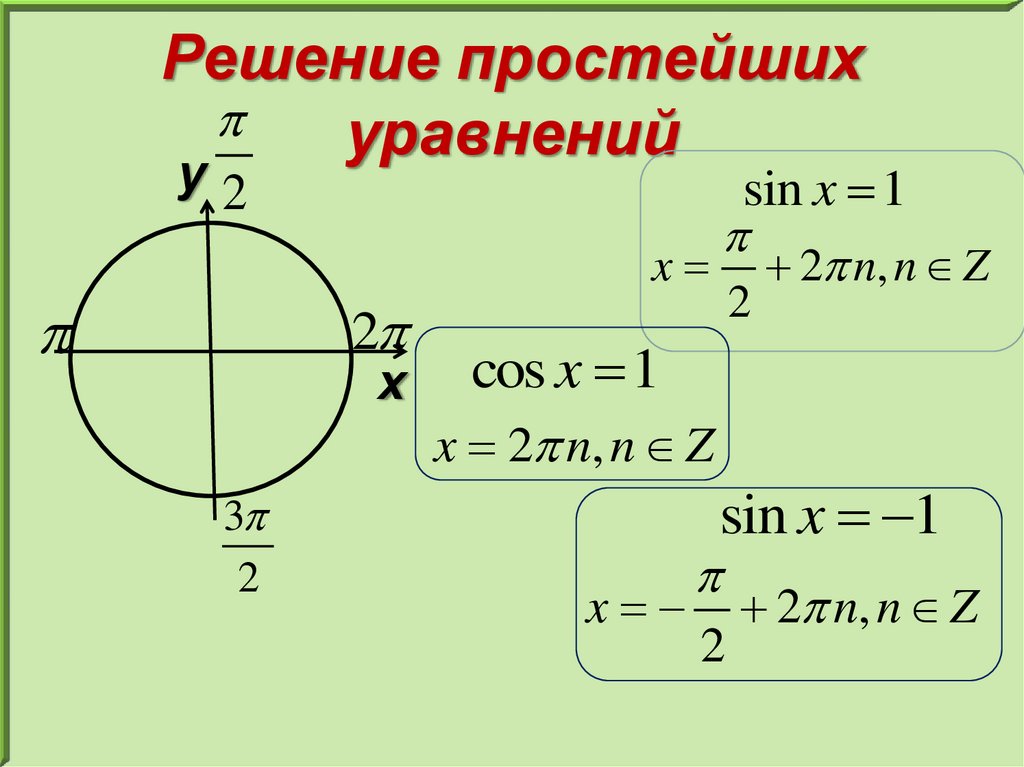
Решение простейшихуравнений
у2
sin x 1
x 2 n, n Z
2
х
3
2
2
cos x 1
x 2 n, n Z
sin x 1
x
2
2 n, n Z
19.
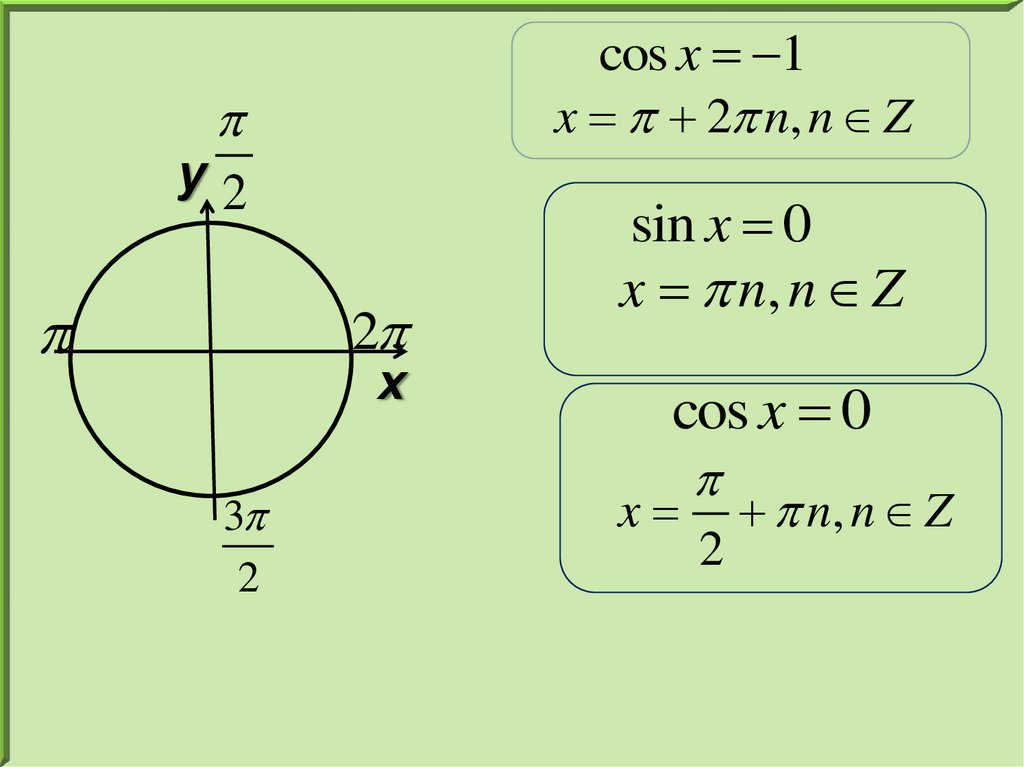
cos x 1x 2 n, n Z
у2
2
х
3
2
sin x 0
x n, n Z
cos x 0
x
2
n, n Z
20.
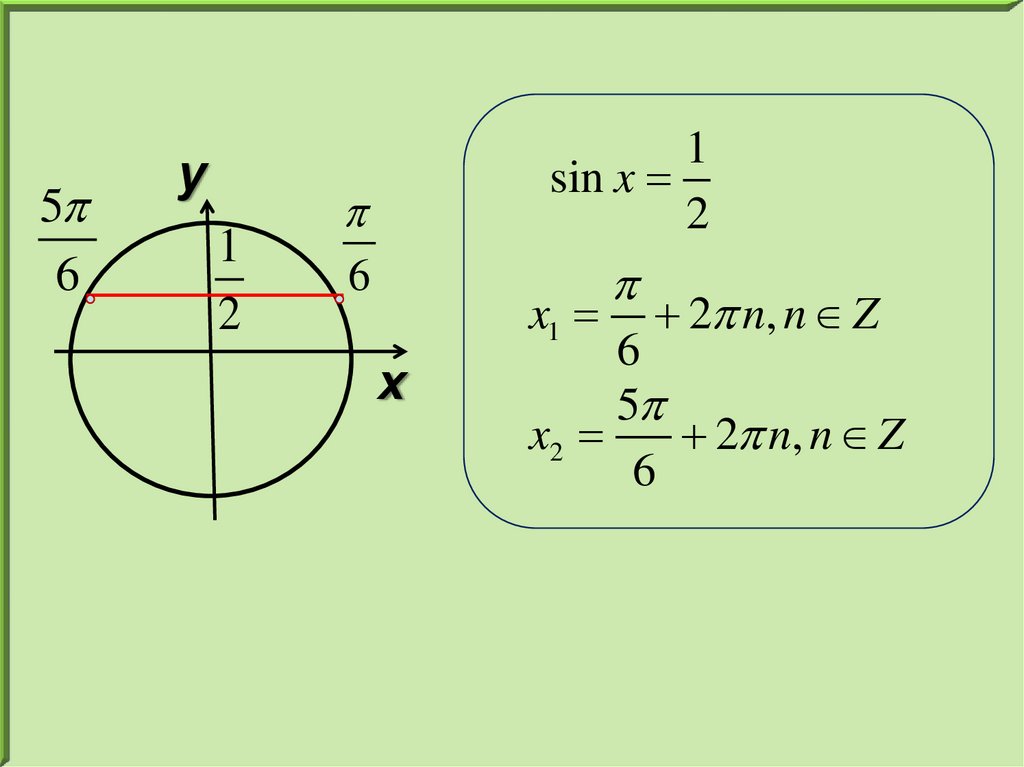
56
у
1
2
1
sin x
2
6
x1
х
2 n, n Z
6
5
x2
2 n, n Z
6
21.
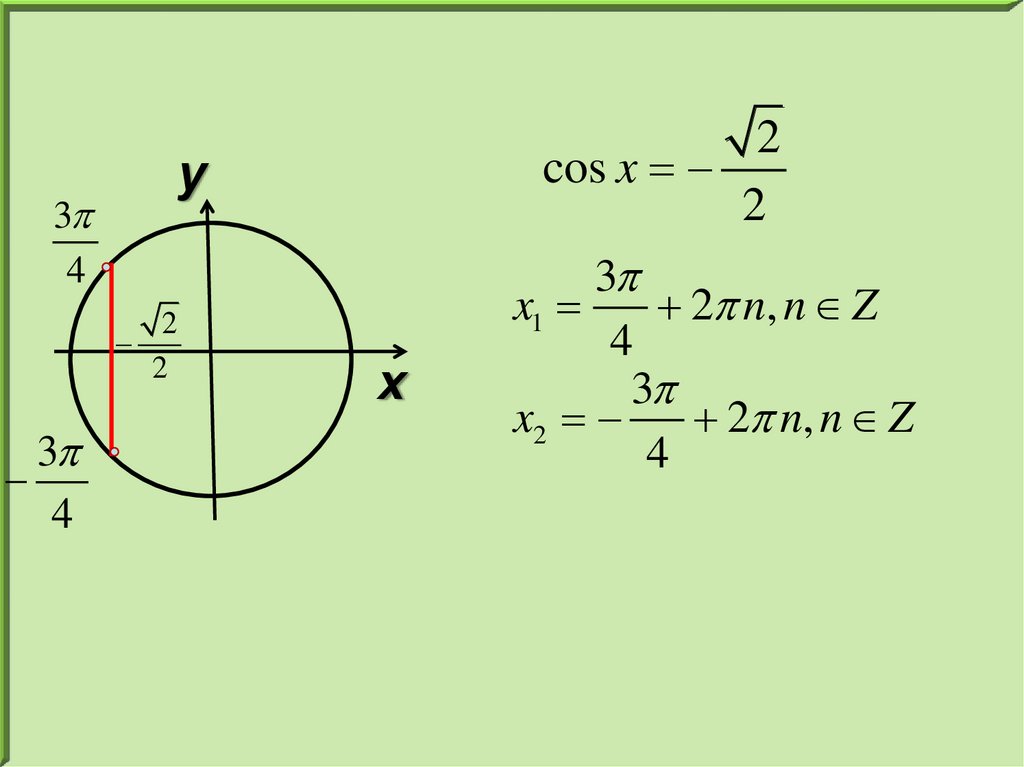
34
у
2
2
3
4
х
2
cos x
2
3
x1
2 n, n Z
4
3
x2
2 n, n Z
4



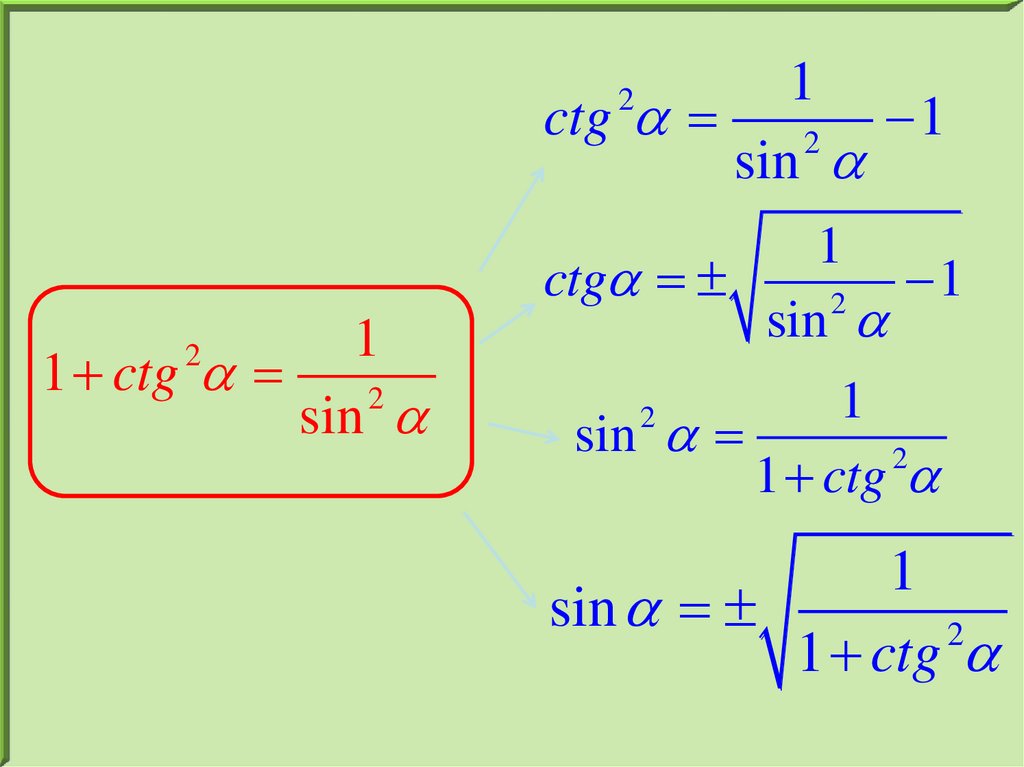



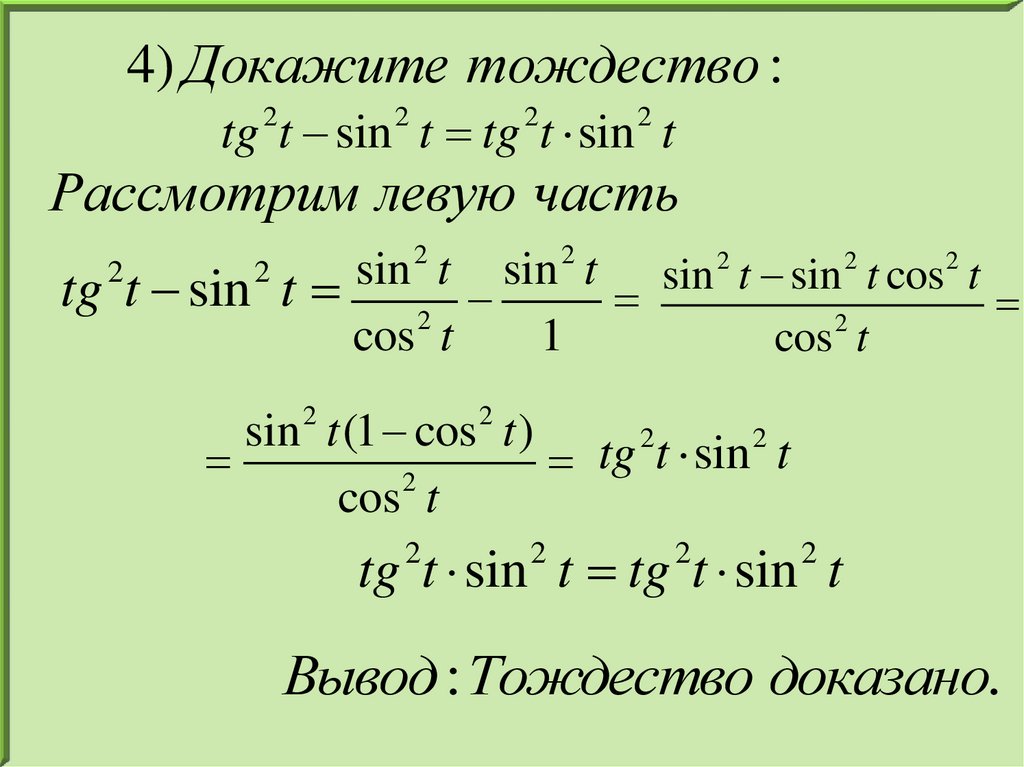



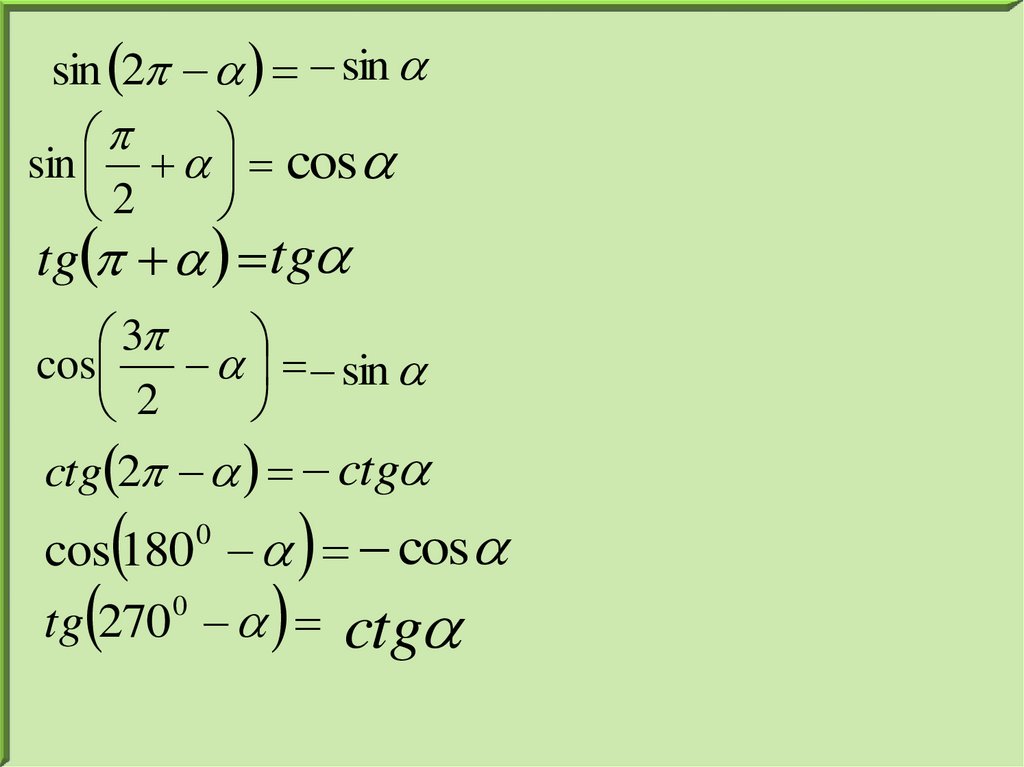
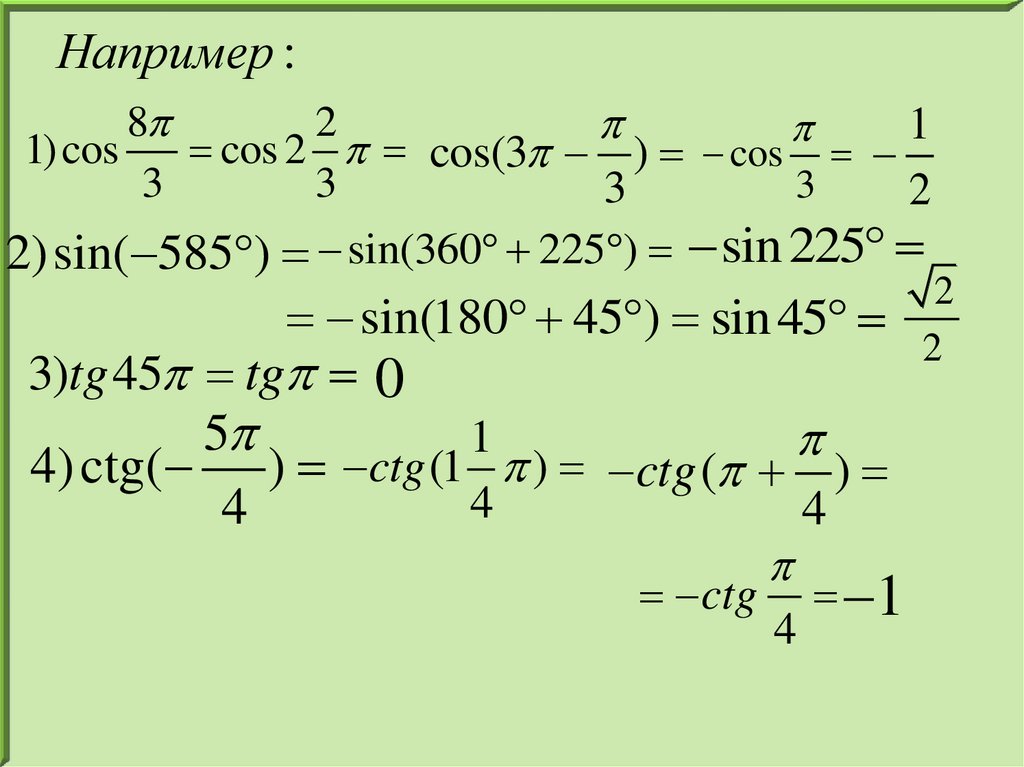
 Математика
Математика








