Похожие презентации:
Траектории управляемых процессов в задачах оптимального управления экономическими системами. Лекция №2
1.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕДИНАМИЧЕСКИМИ СИСТЕМАМИ
ЛЕКЦИЯ №2
Траектории управляемых
процессов в задачах
оптимального управления
экономическими системами
2.
ПОСТРОЕНИЕ ТРАЕКТОРИЙ УПРАВЛЯЕМЫХПРОЦЕССОВ
В подавляющем большинстве задач оптимального
управления непрерывными системами функция u(t),
как уже отмечалось, не является непрерывной.
Вместе с ней не будут непрерывны, что обычно
предполагается в теории дифференциальных
уравнений, правые части уравнений процесса.
В этой лекции мы введем понятие траектории
управляемого процесса для случай, когда
управление u(t) представляет собой разрывную
функцию времени. А также рассмотрим вопросы
практического построения таких траекторий.
3.
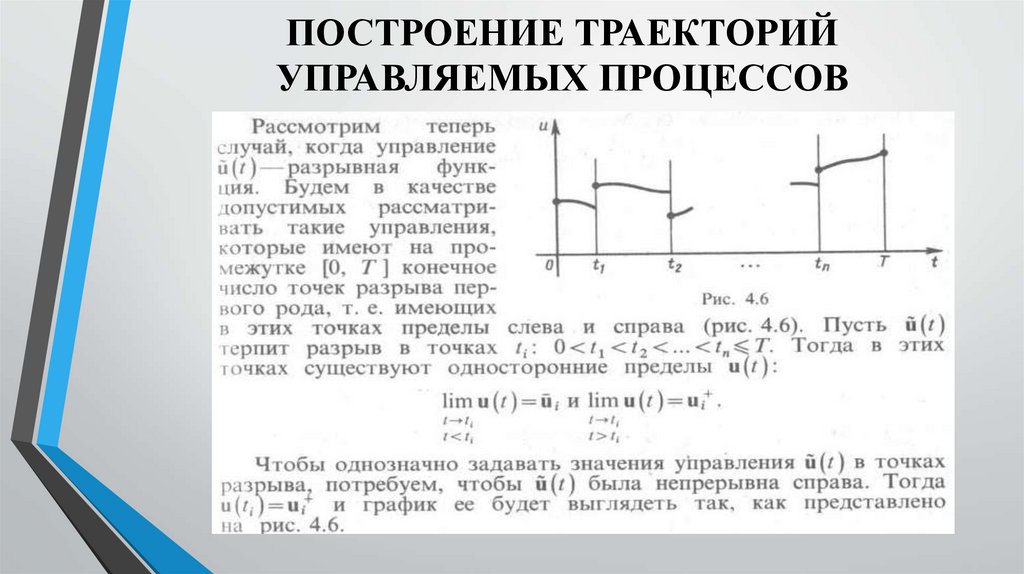
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ
4.
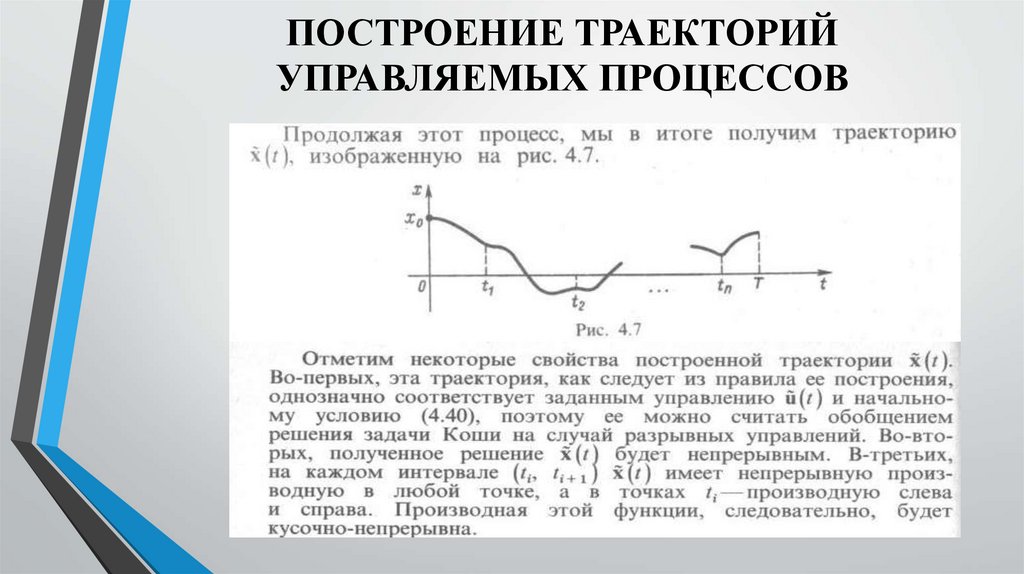
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ
5.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ
6.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ
7.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 1)
8.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 1)
9.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 1)
10.
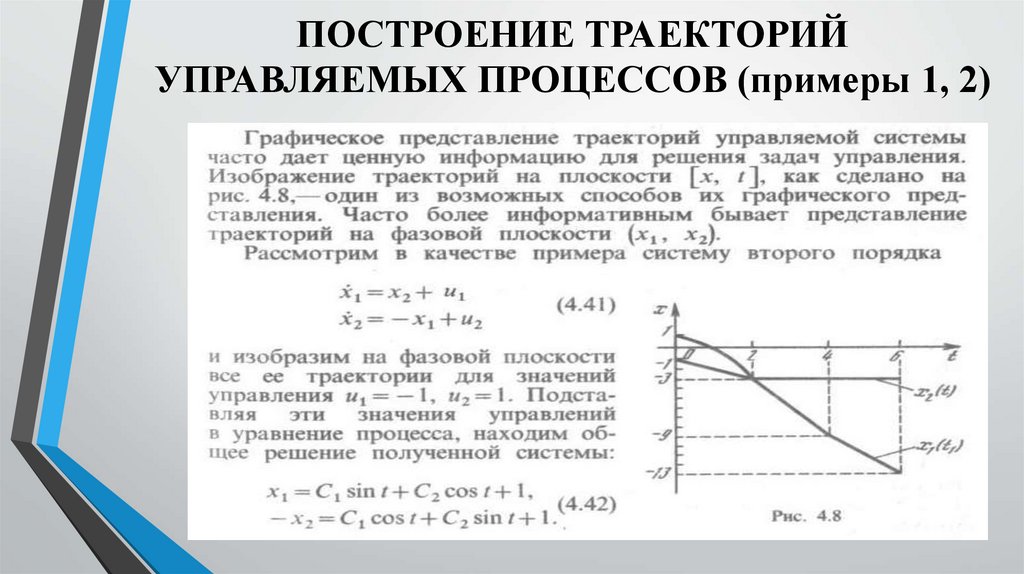
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (примеры 1, 2)
11.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 2)
12.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 2)
13.
ПОСТРОЕНИЕ ТРАЕКТОРИЙУПРАВЛЯЕМЫХ ПРОЦЕССОВ (пример 2)
14.
Пример 1. Однопродуктовая модель оптимальногоОбозначим: X - количество валового объема продукции, производимого в единицу
развития экономики
времени
(интенсивность выпуска валовой продукции),
C – интенсивность потребления.
Однопродуктовая динамическая макроэкономическая модель Леонтьева
представляет собой балансовое соотношение:
Соотношение (2.4.1) показывает, как валовая продукция X распадается на три
слагаемых.
Первая составляющая, aX – это производственные затраты, которые
пропорциональны выпуску продукции X ( a – коэффициент производственных
материальных затрат).























 Физика
Физика