Похожие презентации:
Системы управления химико-технологическими процессами
1.
Божко В.И., Науменко Э.В.СИСТЕМЫ УПРАВЛЕНИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
ЛЕКЦИЯ 3 (Методы математического описания и
исследования динамики линейных многомерных
управляемых систем. Математическое описание и
исследование многомерных систем классическим,
операционным методами и в переменных
пространства состояний. Устойчивость, управляемость
и наблюдаемость систем. Качество переходного
процесса).
1
2.
3.1.1.Математическая
модель
многомерной
системы
Математическая модель линейной непрерывной
многомерной системы в физических переменных входвыход при детерминированных воздействиях может
быть представлена векторным дифференциальным
уравнением вида:
L( p ) y (t ) G ( p )u(t ) N ( p )r (t ) ,
(3.1)
где y(t), u(t), r(t) - векторы выходных переменных,
управляющих
и
возмущающих
воздействий
соответственно;
L( p ) Lij ( p ) , G ( p ) Gij ( p ) , N ( p ) N ij ( p ) полиномные матрицы размерностей n n , n m ,n m1 .
В развернутой форме
2
3.
(3.2)Lij ( p ) l0(ij ) p n l1(ij ) p n 1 ... ln(ij )1 p ln(ij ) . Аналогично
где
для матриц G( p) и N ( p) .
По виду уравнения (3.2) можно охарактеризовать
структуру исследуемой системы, т. е. установить
взаимосвязь ее выходных параметров по матрице L( p ) ,
а также характер и степень воздействия управлений по
матрице G ( p ) и возмущений по матрице N ( p ) на
выходные параметры системы (рис. 3.1).
3
4.
q1(u,r)L11+1
y1
L12
L21
qn(u,r)
y2
Lnn+1
L22+1
q2(u,r)
yn
Lni
qi(u,r)
Lin
yi
Lii+1
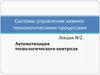
Рис. 3.1. Ненормализованный сигнальный граф
математической модели многомерной системы
4
5.
Ненормализованный сигнальный граф строится всоответствии с уравнением
y (t ) [ L( p ) En ]y (t ) [G ( p )u(t ) N ( p )r (t )] ,
(3.3)
Уравнение
(3.1)
является
общей
формой
математического
описания
как
многомерных
управляемых систем, так и САУ.
3.1.2. Уравнение движения замкнутой САУ
Запишем уравнения движения замкнутой многомерной
САУ по математическим моделям ее элементов и
структуре, представленной на рис. 3.2:
5
6.
r(t)z(t)
z(t)-y2(t)
3
u2(t)
4
u1(t)
1
y1(t)
y2(t)
2
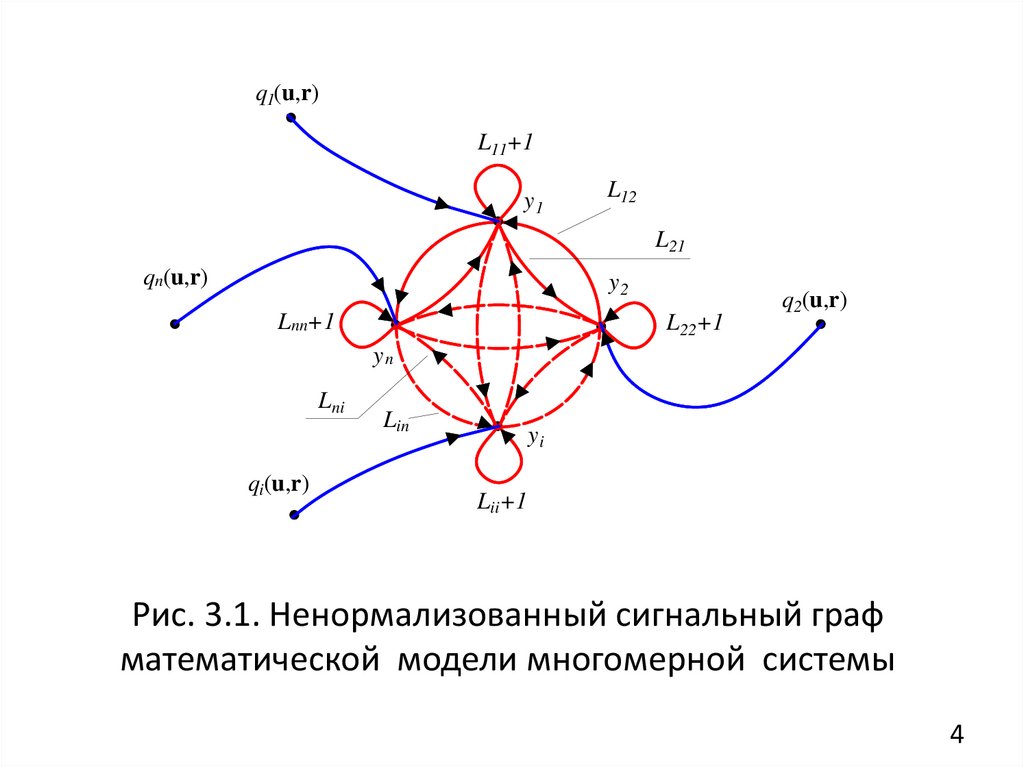
Рис. 3.2. Структурная схема многомерной САУ:
1 управляемая подсистема; 2 измерительная подсистема;
3 управляющая подсистема; 4 исполнительная подсистема
L1( p ) y1(t ) G1( p )u1(t ) N1( p )r (t ) ,
L2 ( p ) y 2 (t ) G2 ( p ) y1(t ) ,
(3.4)
(3.5)
6
7.
L3 ( p )u2 (t ) G1( p )[ z(t ) y 2 (t )] ,(3.6)
L4 ( p )u1(t ) G4 ( p )u2 (t ) .
(3.7)
Полагая, что матрицы Li ( p ) невырожденные,
и
исключая из уравнений (3.4) (3.7) промежуточные
переменные u1 (t ) , u2 (t ) , y 2 (t ) , получим уравнение
САУ в виде
[ L1( p ) G1( p ) L 41( p )G4 ( p ) L 31( p )G3 ( p ) L 21G2 ( p )]y1(t )
G1( p ) L 41( p )G4 ( p ) L 31( p )G3 ( p ) z(t ) N1( p )r (t ).
(3.8)
Уравнение (3.8) можно преобразовать к виду
[ L1( p ) G1( p )W4 ( p )W3 ( p )W2 ( p )]y1(t )
G1( p )W4 ( p )W3 ( p ) z(t ) N1( p )r (t ),
(3.9)
7
8.
гдеLVi ( p )Gi ( p )
1
Wi ( p ) Li ( p )Gi ( p )
, (i 2,3,4).
i
(3.10)
V
L
Здесь через i ( p ) обозначена присоединенная
матрица к Li ( p ) . Матрица Wi ( p ) является
матричной передаточной функцией i-го звена.
Тогда уравнение (3.9) можно представить в виде
[ 2 3 4 L1( p ) G1( p ) LV4 ( p )G4 ( p ) LV3 ( p )G3 ( p ) LV2 ( p )G2 ( p )]y1(t )
2G1( p ) LV4 ( p )G4 ( p ) LV3 ( p )G3 ( p ) z(t ) 2 3 4 N1( p )r (t ) ,
которое можно преобразовать в уравнение (3.1).
Таким образом, уравнение (3.1) представляет
собой математическую модель сложной непрерывной
ДС в терминах вход-выход при детерминированных
8
9.
возмущающих воздействиях и описывает как многомерные объекты управления, так и САУ. Следовательно,методы, применяемые для исследования сложных ДС, в
равной степени применимы к исследованию как
многомерных управляемых систем, которыми являются
ХТП и ХТС, так и к САУ.
Умножим уравнение (3.9) слева на матрицу L1 1 ( p ) и,
учитывая выражения (3.10) и y (t ) y1(t ) , запишем
En W0 ( p)W2 ( p) y (t ) W0 ( p)z(t ) WN ( p)r(t ) ,
(3.11)
где W0 ( p ) W1( p )W4 ( p )W3 ( p ) матричная передаточная функция цепи прямой связи многомерной САУ;
1 V
1
WN ( p ) L1 ( p ) N1 ( p )
L1 ( p ) N1 ( p )
1
матричная передаточная функция подсистемы 1
9
10.
по возмущающему воздействию;En единичная матрица размерности n n .
Решая уравнение (3.11) относительно y (t ), получим
y (t ) En W0 ( p )W2 ( p ) 1W0 ( p ) z(t ) En W0 ( p )W2 ( p ) 1WN ( p )r (t )
(3.12)
Уравнение (3.12) описывает процессы в замкнутой САУ
и называется уравнением автоматического
управления, где En W0 ( p )W2 ( p ) 1W0 ( p ) матричная
передаточная функция САУ по задающему воздействию
z(t ) ; En W0 ( p )W2 ( p ) 1WN ( p ) матричная передаточная
функция САУ по возмущающему воздействию r (t ) .
Отметим, что при изучении устойчивости системы
рассматриваются только ее собственные движения,
10
11.
которые определяются уравнением вида L( p ) 0 .Многомерная система будет устойчивой, когда все корни
характеристического уравнения будут расположены
левее мнимой оси на плоскости комплексного
переменного.
3.1.3. Разомкнутая САУ
Разомкнутая САУ изображена на рис. 3.6, которая
получается путем размыкания обратной связи на
выходе подсистемы 2 . Уравнение движения
разомкнутой САУ
(3.13)
y (t ) W ( p ) z(t ) W ( p )r (t ) .
0
N
Уравнение (3.12) движения замкнутой САУ
отличается от уравнения (3.12) движения
разомкнутой САУ наличием в правой части оператора
11
12.
r(t)z(t)
z(t) y 2 (t)
y(t)
0
y 2 (t)
2
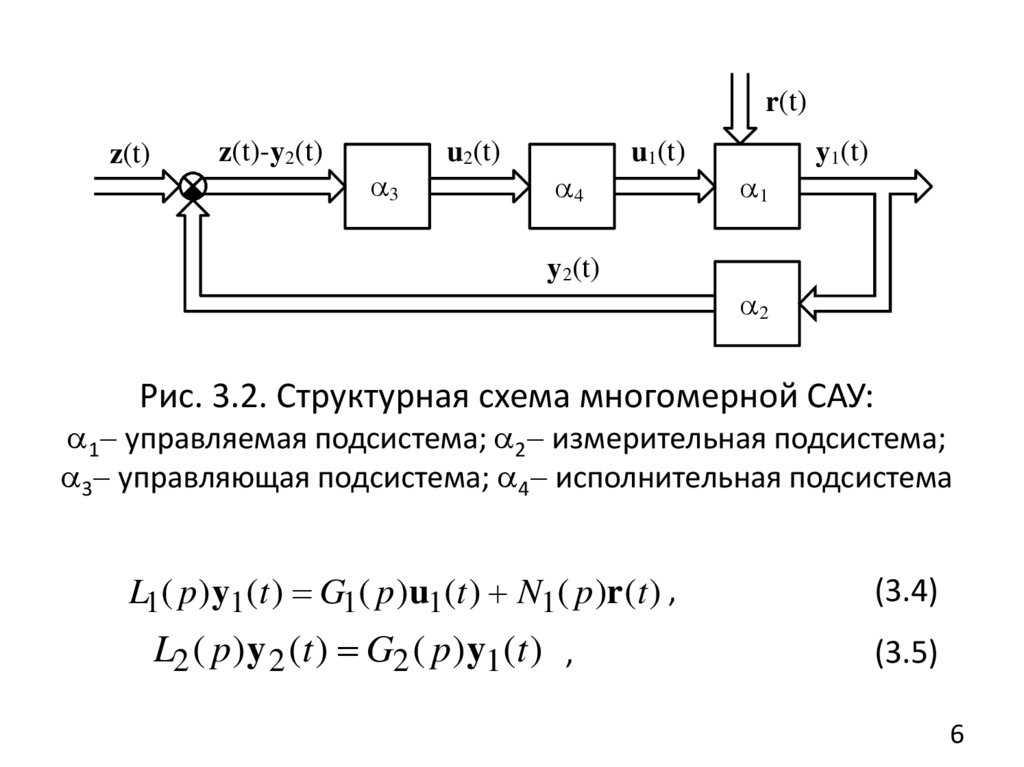
Рис. 3.6. Схема разомкнутой САУ
En W0 ( p)W2 ( p) 1 , который и определяет необходимые
свойства замкнутой системы: как можно точнее
воспроизводить задающее воздействие z(t ) и быть
мало восприимчивой к возмущениям r (t ) .
12
13.
3.2. Операционный метод математического описания иисследования многомерных систем
3.2.1. Применение операционного метода для
определения закона движения многомерной системы
При нулевых начальных условиях операторная форма
записи движения многомерной системы имеет вид (см.
выражение (3.1))
L( s ) Y( s ) G ( s )U( s ) N ( s. )R ( s ) . (3.14)
Уравнение многомерной системы можно записать в
виде
(3.15)
Y( s ) WG ( s )U( s ) WN ( s )R ( s ) ,
V
LV ( s )G ( s ) W ( s ) L 1 ( s ) N ( s ) L ( s ) N ( s ) .
WG ( s ) L ( s )G ( s )
,
N
L ( s)
L ( s)
1
13
14.
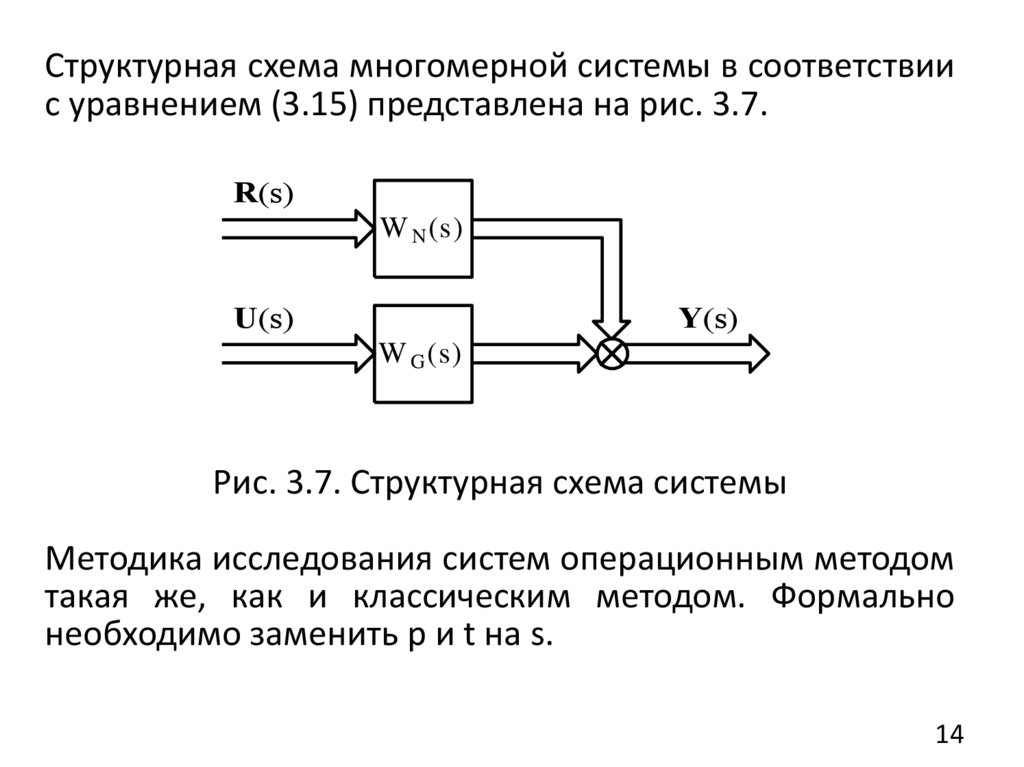
Структурная схема многомерной системы в соответствиис уравнением (3.15) представлена на рис. 3.7.
R(s)
W N (s)
U(s)
Y(s)
W G (s)
Рис. 3.7. Структурная схема системы
Методика исследования систем операционным методом
такая же, как и классическим методом. Формально
необходимо заменить p и t на s.
14
15.
3.3. Математическое описание и исследованиемногомерных систем в переменных пространства
состояний
3.3.1. Уравнения движения многомерной системы
в переменных пространства состояний
Аналитическая запись линейной динамической
многосвязной системы с сосредоточенными
параметрами и постоянными коэффициентами в
переменных пространства состояний имеет следующую
каноническую форму:
dx
Ax(t ) Bu(t ),
x(t0 ) x 0 ,
(3.16)
dt
(3.17)
y (t ) Cx(t ) Du(t ),
15
16.
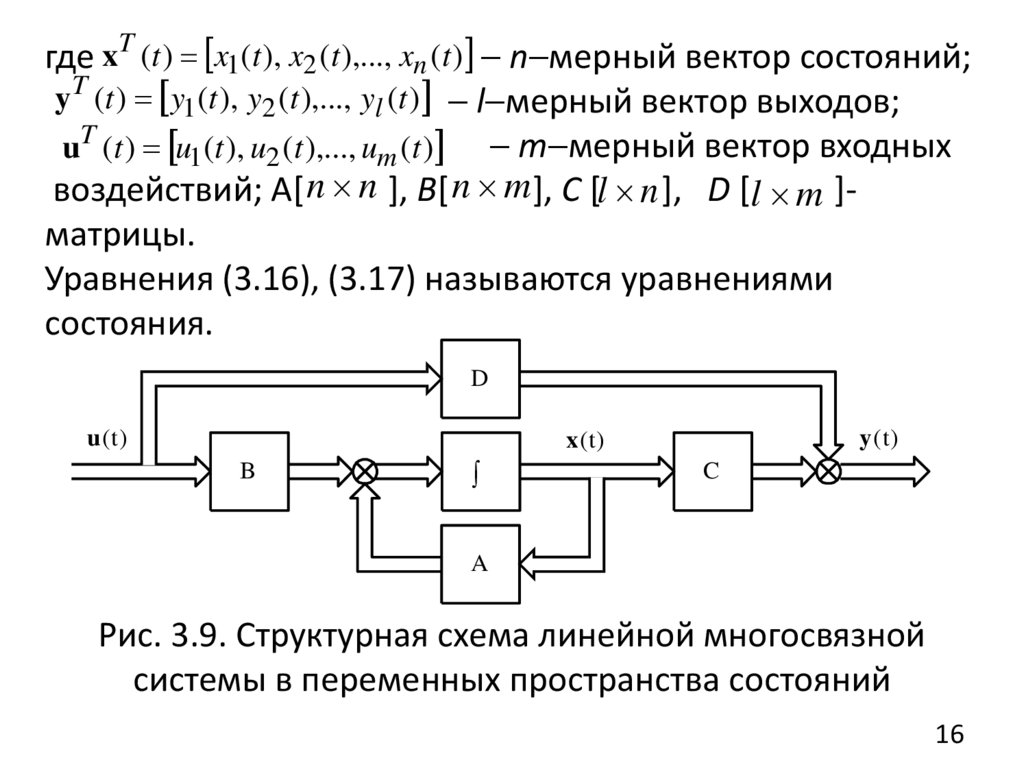
где xT (t ) x1(t ), x2 (t ),..., xn (t ) n мерный вектор состояний;yT (t ) y1(t ), y2 (t ),..., yl (t ) l мерный вектор выходов;
uT (t ) u1(t ), u2 (t ),..., um (t ) m мерный вектор входных
воздействий; A[ n n ], B[ n m], С [l n ], D [l m ]матрицы.
Уравнения (3.16), (3.17) называются уравнениями
состояния.
D
u(t)
y(t)
x(t)
B
C
A
Рис. 3.9. Структурная схема линейной многосвязной
системы в переменных пространства состояний
16
17.
3.3.2. Закон движения системыпространства состояний
в
переменных
t
x(t ) e A(t t0 )x(t0 ) e A(t ) Bu( )d ,
(3.18)
t0
t
A
(
t
t
)
0 x (t ) e A( t ) Bu( )d Du(t ).
y (t ) C e
0
t0
(3.19)
Уравнения
(3.18),
(3.19)
представляют
собой
интегральные
законы
движения
системы
в
соответствующих переменных.
Из уравнений (3.18), (3.19) следует, что движение ДС
происходит как под действием ее начальных условий
(состояний) x(t0 ) – свободное (собственное) движение,
так и под действием внешних воздействий u(t )–
вынужденное движение, а также под одновременным
воздействием этих двух факторов.
17
18.
3.3.3. Переход от уравнения «вход-выход» куравнениям в переменных состояния в нормальной
форме
Рассмотрим переход от уравнения (3.1) к нормальной
форме (на примере дифференциального уравнения n-го
порядка), с которой связан классический метод
интегрирования системы дифференциальных уравнений
первого порядка
(3.20)
при нулевых начальных условиях.
Поделим уравнение (3.20) на коэффициент
получим
a0 0 ,
18
19.
Введем вектори учитывая, что x1 y , px1 x2 , …, pxn 1 xn ,
получим уравнения состояния в нормальной форме
(форме Фробениуса)
19
20.
4. УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ ИНАБЛЮДАЕМОСТЬ СИСТЕМ
4.1. Основные понятия об устойчивости
Под устойчивостью системы понимается ее
способность возвращаться в состояние равновесия
после прекращения действия внешних сил, которые
вывели ее из этого состояния. Для ДС устойчивость
можно определить как свойство свободного движения
системы к своему равновесному состоянию после
начального отклонения ее, вызванного любыми
причинами.
Для
исследования
устойчивости
системы
рассматриваются её свободные движения, т. е. когда на
систему не воздействуют внешние факторы.
20
21.
В математической форме свободные движенияопределяются
решением
однородного
дифференциального уравнения системы.
Для многомерной системы свободные движения
определяются из систем уравнений.
Для:
1. Вход-выход L( p ) y (t ) 0 .
(4.1)
Характеристическое уравнение D( ) L( ) 0 . (4.2)
2. Операторной формы L( s )Y( s ) 0 .
(4.3)
Характеристическое уравнение D( ) L( ) 0. (4.4)
3. Переменных пространства состояний px(t ) Ax(t ) .
(4.5)
Характеристическое уравнение D( ) A En 0 , (4.6)
или в развернутой форме
21
22.
Решение каждого из уравнений (4.2), (4.4), (4.6) позволяетопределить свободное движение системы
n
x (t ) xс (t ) Cix e
i t
n
i t
y
(
t
)
y
(
t
)
C
e
,
,
iy
с
i
где i i j i –
уравнения.
(4.7)
i
корни
характеристического
22
23.
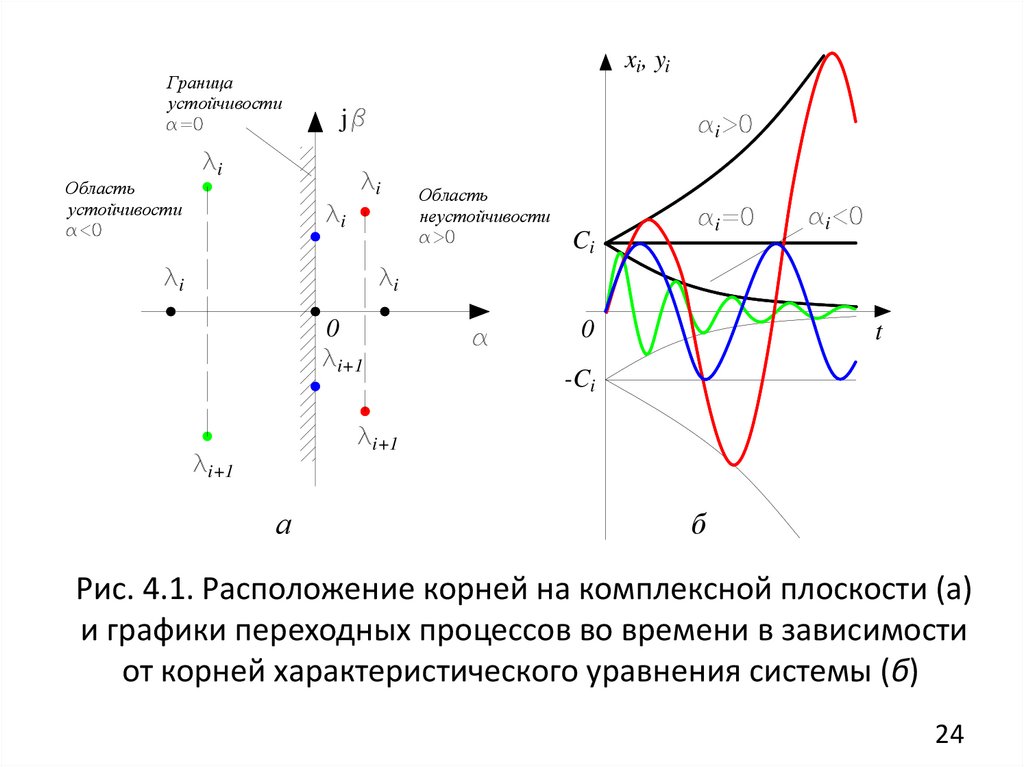
Рассмотрим виды переходных процессов линейнойсистемы в зависимости от знака вещественной
составляющей и значения мнимой составляющей корня
характеристического уравнения, т. е. расположения
корней на комплексной плоскости (рис. 4.1, а):
1) ,i 0 , i 0 , корень i i – процесс
асимптотический сходящийся;
2) i 0 , i 0 , сопряженные комплексные корни
i,i 1 i j i
– процесс колебательный
сходящийся;
3) i 0 , i 0 , корень i i – процесс
расходящийся;
4) i 0 , i 0 , сопряженные комплексные корни
i,i 1 i j i – процесс колебательный
расходящийся;
23
24.
xi, yiГраница
устойчивости
Область
устойчивости
j
i
i
i
Область
неустойчивости
i
i
i
Ci
i
i
0
0
i+1
t
-Ci
i+1
i+1
а
б
Рис. 4.1. Расположение корней на комплексной плоскости (а)
и графики переходных процессов во времени в зависимости
от корней характеристического уравнения системы (б)
24
25.
5) i 0 , i 0 , корень i 0– апериодическая
граница устойчивости;
6) i 0 , i 0 , сопряженные комплексные корни
i,i 1 j i – колебательный процесс на границе
устойчивости (колебательная граница устойчивости).
Система является устойчивой, если вещественная
часть всех корней i i j i ее характеристического
уравнения отрицательна, т. е. i 0 .
По Ляпунову любое заданное движение определяется
как невозмущенное движение системы, а любое другое
движение, отличное от заданного движения
(невозмущенного), определяется как возмущенное.
25
26.
x2,...,xn1
x(t)
x*=0
x1
t
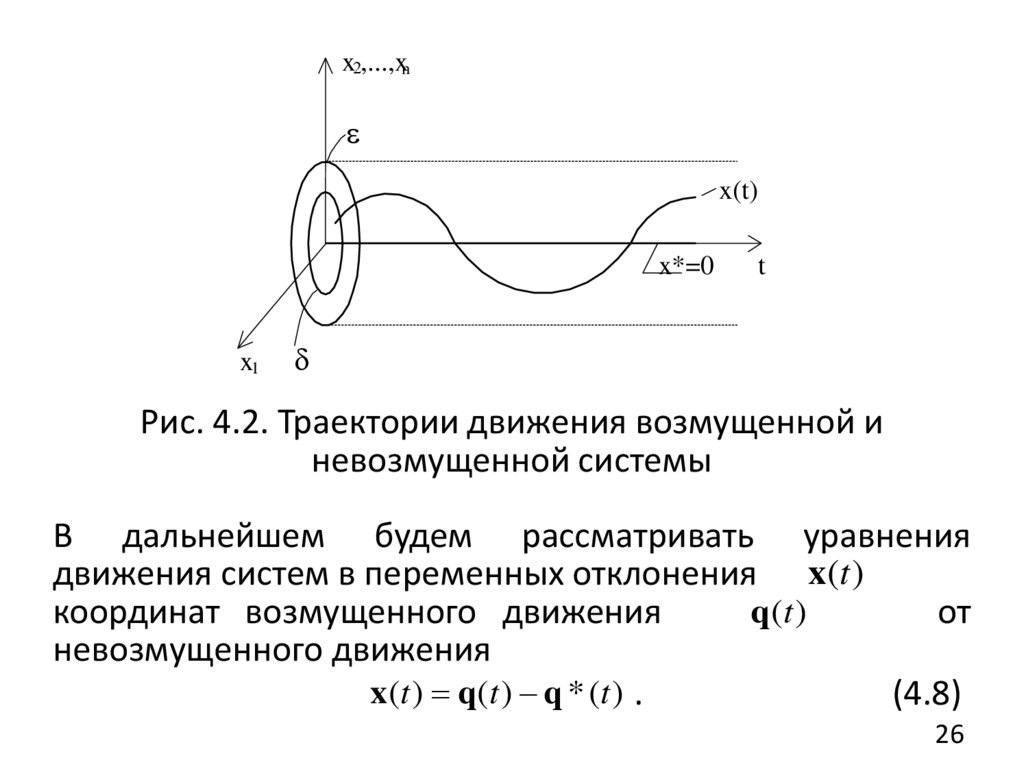
Рис. 4.2. Траектории движения возмущенной и
невозмущенной системы
В дальнейшем будем рассматривать уравнения
движения систем в переменных отклонения x(t )
q(t )
координат возмущенного движения
от
невозмущенного движения
x (t ) q(t ) q * (t ) .
(4.8)
26
27.
Уравнение движения возмущеннойпространстве состояний (рис. 4.2)
dx
F( x(t )) ,
dt
системы
x(t0 ) x 0 ,
а невозмущенной как
x * (t ) 0 ,
которое
соответствует
тривиальному
уравнения (4.9).
в
(4.9)
(4.10)
решению
4.2. Устойчивость по Ляпунову
Невозмущенное движение x * (t ) системы
называется
устойчивым по Ляпунову, если для любого 0 сколь
бы оно мало не было, найдется такое ( ) 0 , что при
начальных условиях
(4.11)
x(t0 ) ( ) ,
27
28.
для любого t t0 выполняется соотношениеx(t ) .
Движение x * ( t ) называется асимптотически
устойчивым, если оно устойчиво по Ляпунову и
lim x(t ) 0 .
t
(4.12)
(4.13)
При этом под нормой вектора в евклидовом
пространстве понимается расстояние точки x(t ) от
начала координат, т. е. длина вектора х:
x
n
2
x
i.
(4.14)
i 1
Геометрическая
интерпретация
устойчивости
по
Ляпунову для двух переменных x1 и x2 в пространстве
состояний представлена на рис. 4.4 траекториями 1 и 2.
28
29.
x23
1
0
2
( )
x1
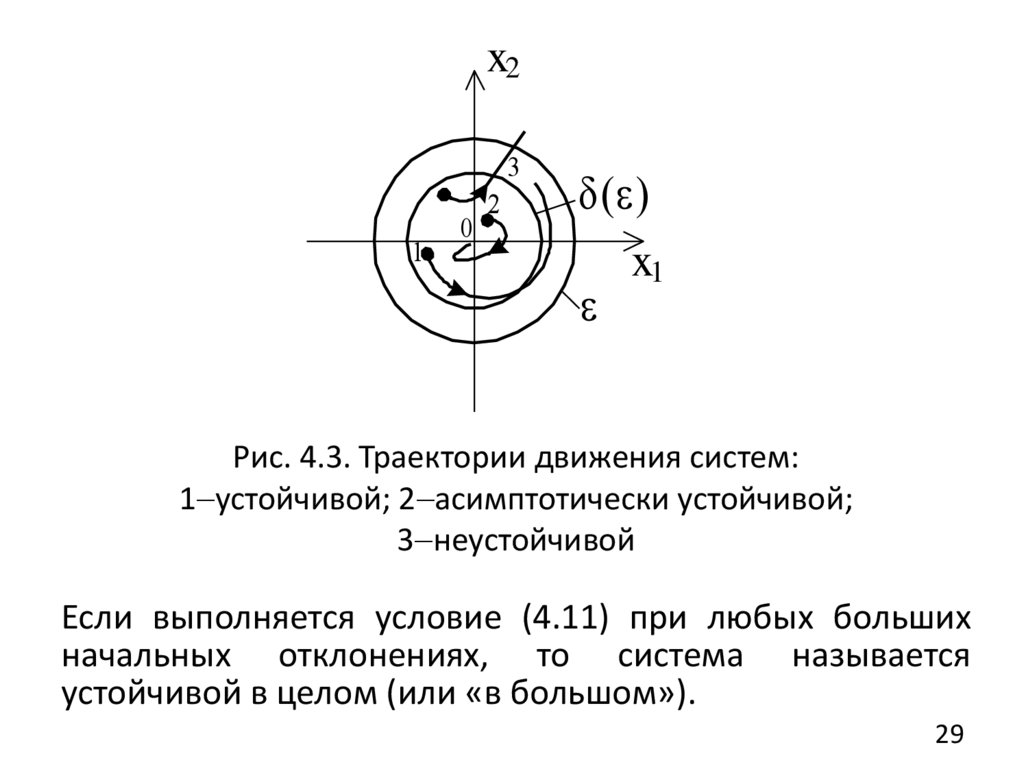
Рис. 4.3. Траектории движения систем:
1 устойчивой; 2 асимптотически устойчивой;
3 неустойчивой
Если выполняется условие (4.11) при любых больших
начальных отклонениях, то система называется
устойчивой в целом (или «в большом»).
29
30.
Для линейной системы возможны три случаяисследования устойчивости:
1. Линейная многомерная система (4.9) устойчива тогда
и только тогда, когда все вещественные части
собственных (характеристических) чисел j j ( A)
имеют отрицательные значения, т. е.
Re j 0 – асимптотическая устойчивость;
2. Если хотя бы один корень характеристического
уравнения D( ) 0 имеет нулевую вещественную
часть, т. е. Re j 0 , то линейная многомерная
система находится на границе устойчивости;
3. Если хотя бы один корень характеристического
уравнения D( ) 0 имеет
положительную
вещественную часть, т. е. Re j 0 ,
то
система
неустойчива.
30
31.
Для линеаризованной системы возможны также трислучая исследования устойчивости по первому
приближению: пп. 1 и 2 – совпадают;
3. Если существуют корни характеристического
уравнения D( ) 0 с нулевой вещественной частью при
всех остальных отрицательных, то для определения
устойчивости невозмущенного движения x * (t ) по
первому приближению необходимо специальное
исследование полного уравнения с нелинейностями.
4.3. Алгебраический критерий устойчивости Гурвица
(1895 г.)
Суть критерия состоит в том, что не решая
дифференциального уравнения ДС, а также не
производя громоздких вычислительных операций для
непосредственного вычисления собственных значений
по соответствующим матрицам ДС (4.1), (4.3). (4.6),
31
32.
элементы которых зависят от исходных физическихпараметров, выбора базиса пространства состояний,
можно по определителям Гурвица определить
устойчивость или неустойчивость ДС.
Характеристическое уравнение ДС D( ) 0 в
развернутой форме имеет вид
(4.15)
которое
соответствует
однородному
дифференциальному уравнению линейной системы n-го
порядка
(4.16)
тогда для устойчивости линейной системы n-го
порядка необходимо и достаточно, чтобы были
положительными
n
главных
(диагональных)
определителей Гурвица, т. е. i 0
,
32
33.
(4.17)(4.18)
33
34.
составленных из коэффициентовхарактеристического уравнения (4.15) рассматриваемой
системы. Условия устойчивости для системы n-го
порядка записываются в виде определителей Гурвица,
получаемых
из
квадратной
матрицы
(4.17)
коэффициентов характеристического уравнения (4.15).
Определитель i-го порядка Гурвица выделяется из
таблицы отчеркиванием одинакового числа i строк и
столбцов, начиная от левого верхнего угла таблицы, и
имеет вид (4.18). Положительность последнего
определителя Гурвица
n n n 1 ,
(4.19)
при n 1 0 сводятся к положительности свободного
члена n характеристического уравнения (4.16).
34
35.
Положительныезначения
коэффициентов
характеристического уравнения системы являются
необходимым,
но
не
достаточным
условием
устойчивости линейной системы.
Алгебраический критерий Гурвица удобен для
исследования в аналитической форме на устойчивость
линейных систем не выше четвертого порядка. При
численном задании всех коэффициентов легко
проверяется устойчивость линейных систем любого
порядка.
4.4. Частотный критерий устойчивости
Найквиста-Михайлова (1932, 1936 гг.)
Критерий позволяет судить об устойчивости замкнутой
системы по виду амплитудно-фазовой характеристики
разомкнутой системы.
35
36.
jV ( )1. Неустойчивая система.
2
2. Система на границе устойчивости.
3. Устойчивая система.
1
-1
8
-2
0
-1
1
2
3
0
U( )
-2
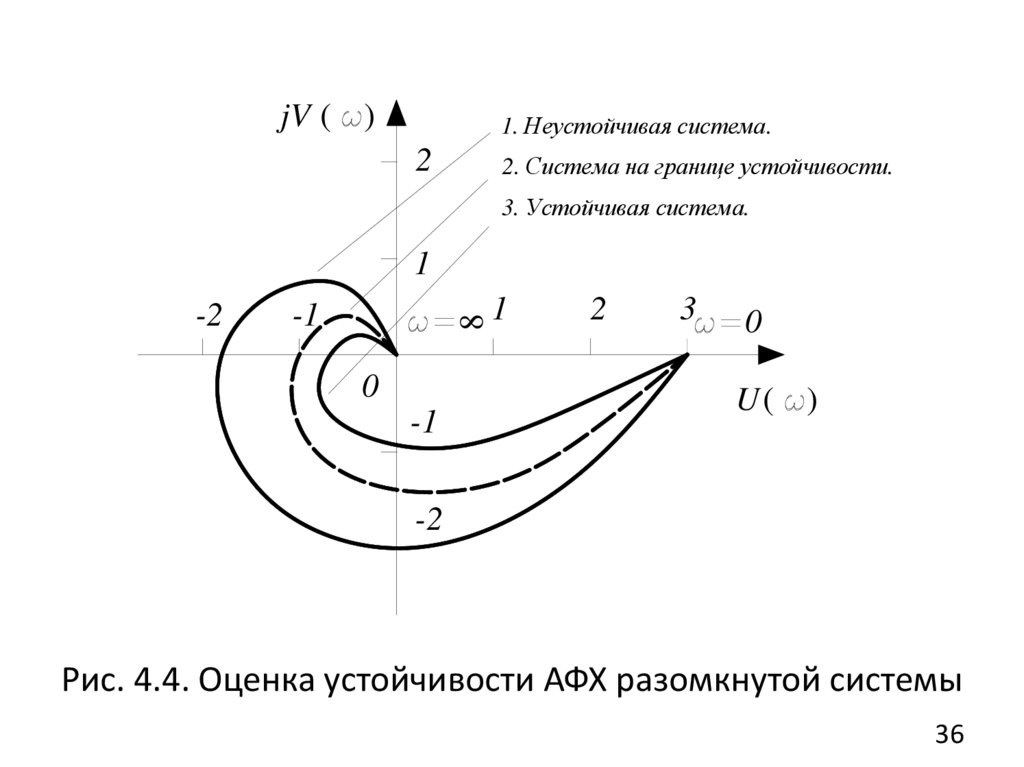
Рис. 4.4. Оценка устойчивости АФХ разомкнутой системы
36
37.
В соответствии с частотным критерием устойчивостиНайквиста (Найквиста-Михайлова) система устойчива в
замкнутом состоянии, если она устойчива в
разомкнутом состоянии и ее амплитудно-фазовая
характеристика при изменении частоты от 0
до
не охватывает точку в комплексной плоскости с
координатами 1, j 0 (рис. 4.4).
4.5. Качество переходного процесса
Качество переходного процесса в ДС определяется по
показателям, которые характеризуют отклонение
реального процесса от желаемого; они показывают как
точно и быстро после нанесения единичного
ступенчатого воздействия (при нулевых начальных
условиях) в системе устанавливается статическое
(равновесное) состояние.
37
38.
u, r1
0
t
а
y3
y2
-
z зд,r=y0
0
tпп
y ст
+
y дин
y1
z зд,u , y
8
y
t
б
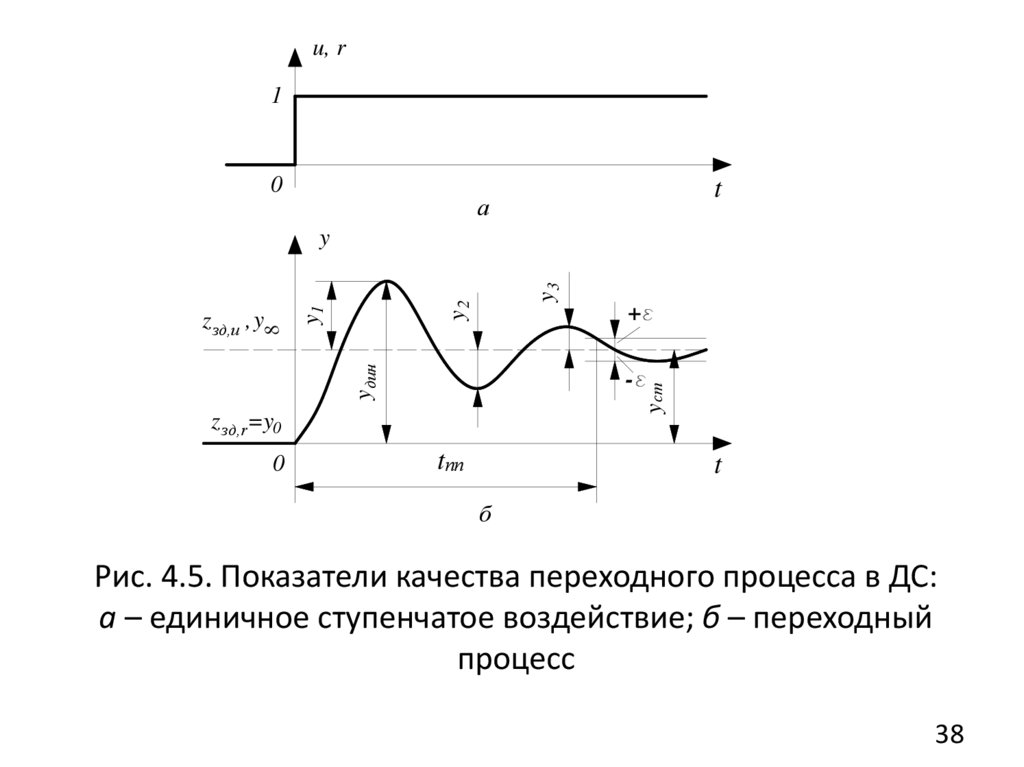
Рис. 4.5. Показатели качества переходного процесса в ДС:
а – единичное ступенчатое воздействие; б – переходный
процесс
38
39.
Качествопереходного
процесса
количественно
оценивается следующими показателями (рис. 4.5).
Статическая ошибка управления
yст y z .
(4.20)
Динамическая ошибка управления
yдин ymax z .
(4.21)
Время переходного процесса tпп – время, в течение
которого управляемая величина достигает нового
установившегося значения с некоторой заранее
установленной точностью
от момента подачи
управляющего или возмущающего воздействия. Время
переходного процесса в САУ иногда называют временем
регулирования t р tпп .
Перерегулирование – максимальное отклонение
управляемой величины от установившегося значения,
выраженное в процентах, от y ст при воздействии
39
40.
по заданию z (t )yдин yст
100%
yст
при
уст 0 ,
(4.22)
по возмущению r (t )
y2
100% .
y1
(4.23)
Интеграл от квадрата ошибки (ИКО) управления –
площадь от квадрата амплитуды между кривой
переходного процесса y (t ) и новым установившимся
выходом y системы:
I ( y (t ) y ) 2 dt .
(4.24)
0
40
41.
Чем меньше статическая и динамическая ошибки, времяуправления и т. п., тем выше качество переходного
процесса.
На форму и качество переходного процесса САУ влияют
свойства ОУ, тип закона управления УУ и степень его
воздействия на объект.
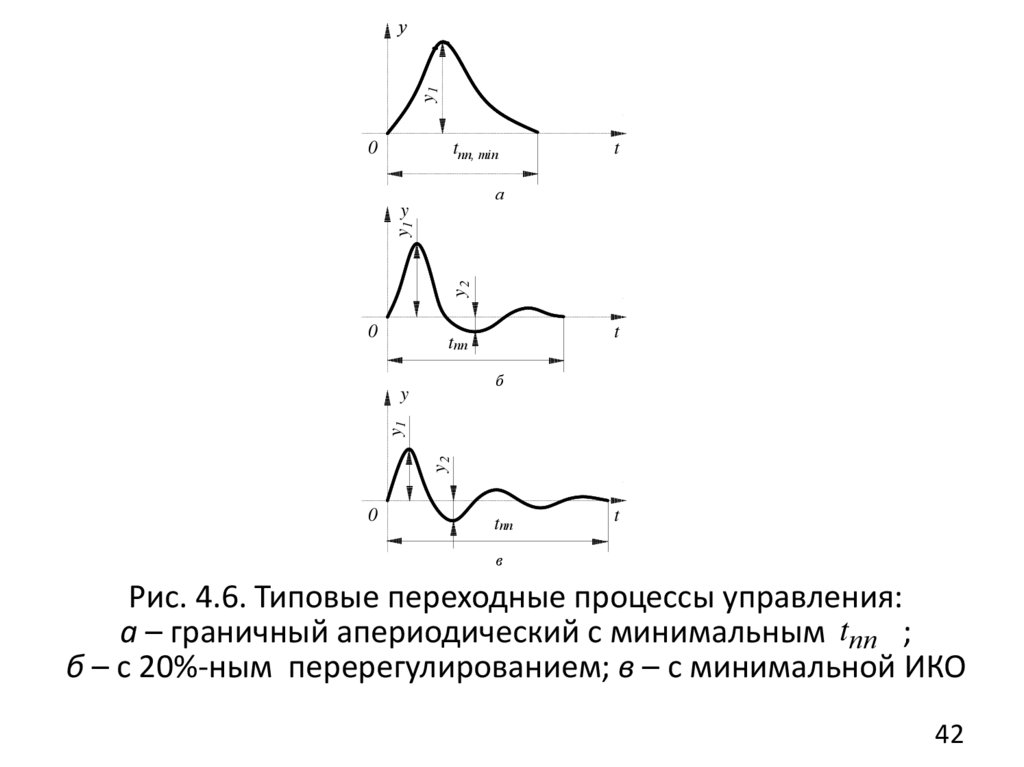
4.6. Типовые оптимальные переходные процессы
Из устойчивых переходных процессов в качестве
оптимального с точки зрения требований технологии
ХТП
выбирают
один
из
трех
типовых
процессов (рис. 4.6).
41
42.
y10
tпп, min
t
а
y2
y1
y
0
t
tпп
б
y2
y1
y
0
tпп
t
в
Рис. 4.6. Типовые переходные процессы управления:
а – граничный апериодический с минимальным tпп ;
б – с 20%-ным перерегулированием; в – с минимальной ИКО
42
43.
4.7. Управляемость и наблюдаемость многомерныхсистем
4.7.1. Управляемость и стабилизируемость
многомерных систем
4.7.1.1. Управляемость
С понятием управляемости тесно связано понятие
процесса управления, т. е. это принципиальная
возможность перевода системы из состояния x н (t0 ) в
заданное состояние x f (T )
на интервале времени
(t0 , T ] под действием управления u(t ) .
Система называется полностью управляемой, если под
действием некоторого управления u(t ) она
может
быть переведена из любого начального состояния x(t0 )
43
44.
в любое наперед заданное состояние x(t f ) за конечноевремя t f t0 0 .
Система
называется
неполностью
(частично)
управляемой, если имеется подмножество начальных
состояний, из которых достижение произвольного
желаемого состояния за конечное время невозможно.
Система называется полностью неуправляемой, когда из
любого множества начальных состояний достижение
произвольного желаемого состояния за конечное время
невозможно.
Условия управляемости по состояниям для линейной
системы вида (3.16) определяются теоремой (или
критерием) Калмана: система будет вполне управляема
тогда и только тогда, когда ранг матрицы управляемости
44
45.
Lc размерности n nmравен n, т. е.
rank Lc n ,
где
(4.25)
,
(4.26)
n – размерность пространства состояний (вектора
состояний x(t ) ).
Из выражения (4.26) следует, что управляемость
системы по состояниям x (t ) определяется строением
матриц А и В.
Если rank Lc n , то система будет неполностью
управляемой, а при rank Lc 0 –
полностью
неуправляемой.
Ранг матрицы М ( rank M ) – наибольший из порядков
45
46.
отличных от нуля миноров, порождаемых матрицей M.Если матрица M прямоугольная размером n m , то
rank M r n, m .
При
управляемости
обеспечивается
влияние
управления на все координаты вектора состояния.
Управляемость по выходам. Система будет полностью
управляемой по выходам y (t )
тогда и только
тогда, когда ранг матрицы управляемости
,
(4.27)
равен l, т. е.
(4.28)
rank L0c l ,
где l – размерность пространства выходов системы
(вектора выходов y (t ) ).
46
47.
0Если rank Lc l , то система будет неполностью
управляемой по выходам, а при rank L0c 0 – полностью
неуправляемой.
4.7.1.2. Стабилизируемость
Стабилизируемость - обеспечение с помощью САУ
постоянных
(стабильных)
значений
заданных
параметров процесса в соответствии с технологическим
регламентом. Иначе, стабилизируемость характеризует
способность системы находиться в заданном состоянии,
которое обычно принимается за начало координат
пространства состояний, как угодно долго после
перевода ее в данное состояние. Если рассматривать
свободное движение устойчивой системы, то в силу
того, что все собственные значения i матрицы А (3.16)
47
48.
имеют Re i 0 , получаем, что все ее решения приt стремятся к началу координат. Следовательно,
устойчивая
система
априори
стабилизируема.
Совершенно иная ситуация наблюдается при свободных
движениях нейтральных и неустойчивых систем, так как
в этом случае при t уже не все решения системы
стремятся к началу координат. Поэтому для
стабилизируемости таких систем необходимо в контур
обратной связи вводить УУ. Следовательно, линейная
n
система (3.16) в R называется стабилизируемой, если
существует такое линейно зависимое от x (t ) управление
u(t ) Kx(t ) ,
(4.29)
что система
dx
(4.30)
Ax(t ) BKx(t ) ( A BK )x(t ) ,
dt
48
49.
устойчива, т. е. найдется такая матрица K, что вседействительные части собственных значений матрицы
( A BK ) будут отрицательны. Матрица К - матрица
обратной связи. Из уравнения (4.30) следует, что любая
управляемая система путем выбора матрицы обратной
связи К стабилизируема.
Аналогично определяется стабилизируемость по
выходам, т. е.
dx
( A BKC )x(t ) .
u(t ) Ky (t ) и
(4.31)
dt
Следовательно, стабилизируемость системы достигается
таким выбором матрицы К, которая обеспечивает
отрицательность
всех
действительных
частей
собственных значений матрицы ( A BKC ) .
49
50.
4.7.2. Наблюдаемость и оценивание координатсостояния многосвязных систем
4.7.2.1. Наблюдаемость
В ХТП и ХТС выходными параметрами y (t ) являются
физические величины, которые можно измерить
(наблюдать) и по которым осуществляется оценивание
состояния x(t ) и ведение процесса. В связи с этим
важное значение приобретает понятие наблюдаемости
системы по Калману.
Система будет полностью наблюдаемой, если по
измеренным выходам y (t ) и известным управлениям
u(t ) на интервале времени [t0 , t1 ] можно определить
все координаты вектора состояния x(t0 ) .
50
51.
Система будет неполностью наблюдаемой, если поизмеренным выходам y (t ) и известным управлениям
u(t ) на интервале времени [t0 , t1 ] можно восстановить
не все координаты вектора состояния x ( t0 ) .
Стационарная линейная система (3.16), (3.17) будет
полностью наблюдаемой тогда и только тогда, когда ранг
матрицы наблюдаемости Lo [ n nl ] равен n, т. е.
где
rank Lo n ,
(4.32)
. (4.33)
Если rank Lo r и r n ,
то
система
будет
неполностью наблюдаемой. При r 0 система будет
полностью ненаблюдаемой.
51
52.
4.7.2.2. Оценивание координат состоянияПри функционировании ХТП и ХТС может возникнуть
ситуация, когда необходимо осуществлять управление
по абстрактным (фиктивным) или не подлежащим
измерению координатам состояния. Однако если
система
полностью
наблюдаема,
то
можно
«восстановить» неизмеряемые координаты состояния
xi (t ) по их косвенной оценке путем введения так
называемого «наблюдателя» по Калману, т. е.
устройства оценки состояний детерминированной
системы. Оценка вектора состояний
ведется по
наблюдаемым физическим выходам y (t ) системы. Таким
образом, метод оценки вектора состояния дает
возможность
«восстановить»
неизмеримые
52
53.
(не подлежащие непосредственному измерению)координаты вектора состояния в виде xˆi (t) xi (t) и
использовать «восстановленный» вектор состояния
системы для решения задач управления.
В случае, когда l n (3.16), (3.17) и D=0, т. е. матрица С
является квадратной и невырожденной размерности
n n , то вектор состояния определяется однозначно
как x(t ) C 1y (t ) . И в соответствии с (4.32) система
полностью наблюдаемая.
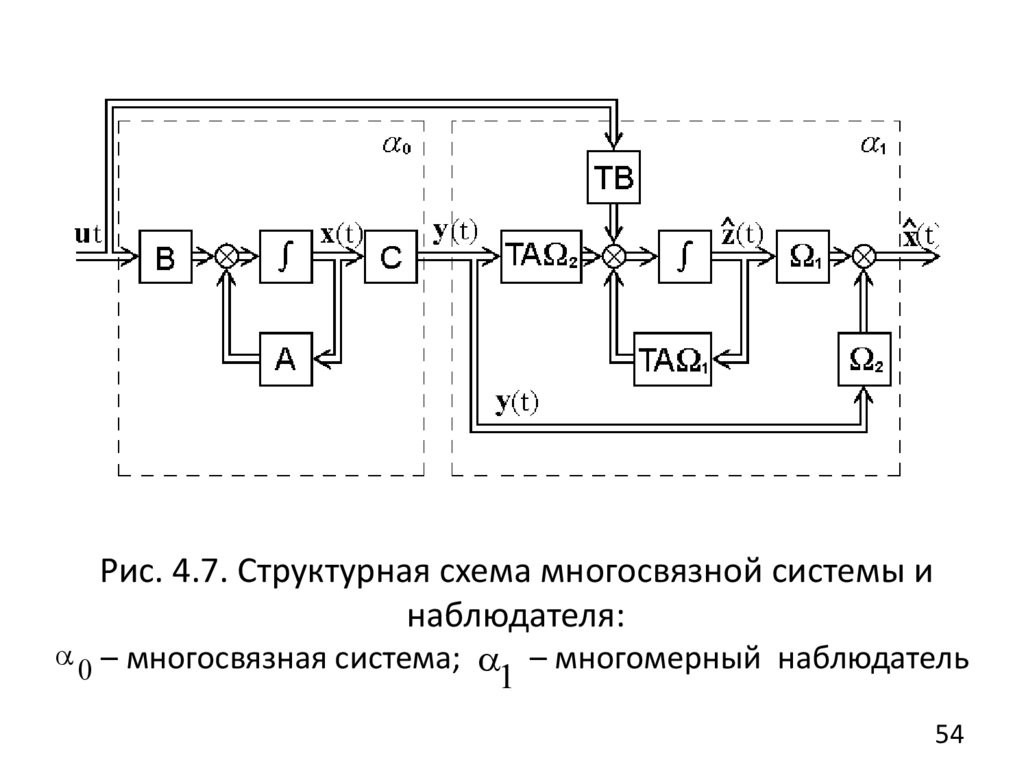
Для общего случая, когда l n , необходимо применение
«наблюдателя» – подсистемы, которая позволяет
восстановить вектор состояния системы (рис. 4.7).
53
54.
Рис. 4.7. Структурная схема многосвязной системы инаблюдателя:
0 – многосвязная система; – многомерный наблюдатель
1
54
55.
Уравнение наблюдателя для оценкиопределяется выражением
zˆ (t )
и
(4.34)
(4.35)
Здесь zˆ (t ) Tx(t ) ; T , i - определенным образом
вводимые матрицы: Ω1T Ω2C E и ( E Ω2C ) A .
Матрица ( E Ω2C ) A должна имела собственные числа,
обеспечивающие заданную скорость сходимости оценки
оцениваемого
ẑ(t ) к истинному значению
вектора x (t ) .
55
56.
Контрольные вопросы1. Что такое устойчивость системы?
2. Какие движения системы исследуются для определения ее
устойчивости?
3. Записать уравнения свободных движений многомерных
систем, представленных уравнениями в переменных входвыход, операторной форме и в переменных пространства
состояний.
4. Записать характеристические уравнения многомерных
систем, представленных уравнениями в переменных входвыход, операторной форме и в переменных пространства
состояний.
5. Дать характеристику переходным процессам систем в
зависимости
от
расположения
корней
их
характеристических уравнений на комплексной плоскости.
6. Что такое по Ляпунову невозмущенное и возмущенное
движения системы?
56
57.
7. Дать определение устойчивости по Ляпунову.8. Изобразить в фазовой плоскости траектории движения
устойчивой, асимптотически устойчивой и неустойчивой
систем.
9. Рассмотреть три случая исследования устойчивости
линеаризованной системы.
10. Записать необходимые и достаточные условия
устойчивости линейной системы n-порядка по Гурвицу.
11. Записать показатели качества переходного процесса и
охарактеризовать их назначение.
12. Назвать и охарактеризовать оптимальные типовые
переходные процессы с точки зрения требований
технологии к ХТП.
13. Что такое управляемость системы и дать определение
управляемости по Калману.
14. Что такое стабилизируемость системы?
15. Что такое наблюдаемость ХТП?
57
58.
БЛАГОДАРЮ ЗА ВНИМАНИЕ.УСПЕХОВ!
58














































 Физика
Физика