Задачи на построение сечений

1.

2.

1.Секущая плоскость тетраэдра(параллепипеда)-это
любая плоскость, по обе стороны от которой имеются точки
данного тетраэдра (параллепипеда).
2.Многоугольник, сторонами которого являются отрезки,
пересекающие грани тетраэдра (параллепипеда)
называется сечением тетраэдра (параллепипеда).

3.

Секущей плоскостью тетраэдра
(параллелепипеда) называется любая
плоскость, по обе стороны от которой
имеются точки данного
многогранника.
Секущая плоскость пересекает грани
многогранника по отрезкам.
Многоугольник, сторонами которого
являются эти отрезки, называется
сечением многогранника (тетраэдра,
параллелепипеда).

4.

• Две плоскости пересекаются по прямой (эта аксиома и дала названию
метода – под «следом» понимается прямая пересечения какой-либо грани
многогранника и секущей плоскости).
• Получение «следа» сводится к получению двух точек, принадлежащих
одновременно какой-нибудь грани многогранника и секущей плоскости
• Точки получаются как пересечение двух прямых, принадлежащих
одной и той же плоскости.
Не забудьте, что прямая
бесконечными в пространстве фигурами!
ПРИМЕЧАНИЕ.
и
плоскость
являются

5.

Метод следов включает три важных пункта:
1. Строится линия пересечения (след) секущей плоскости с плоскостью
основания многогранника.
2. Находим точки пересечения секущей плоскости с ребрами многогранника.
3. Строим и заштриховываем сечение.

6.

Плоскость сечения может задаваться:
1) тремя точками, не лежащими на одной
прямой;
2) прямой и точкой, не лежащей на ней;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к
первому, выбирая на прямых удобные
для нас точки.

7.

Так как тетраэдр имеет четыре грани, то его
сечениями могут быть только треугольники и
четырёхугольники.

8.

Параллелепипед имеет шесть граней. Его
сечениями могут быть треугольники,
четырёхугольники, пятиугольники и
шестиугольники.
С
В
А
В
M
L
С
А
К
D
N
E

9.

Сечения тетраэдра и параллелепипеда

10.

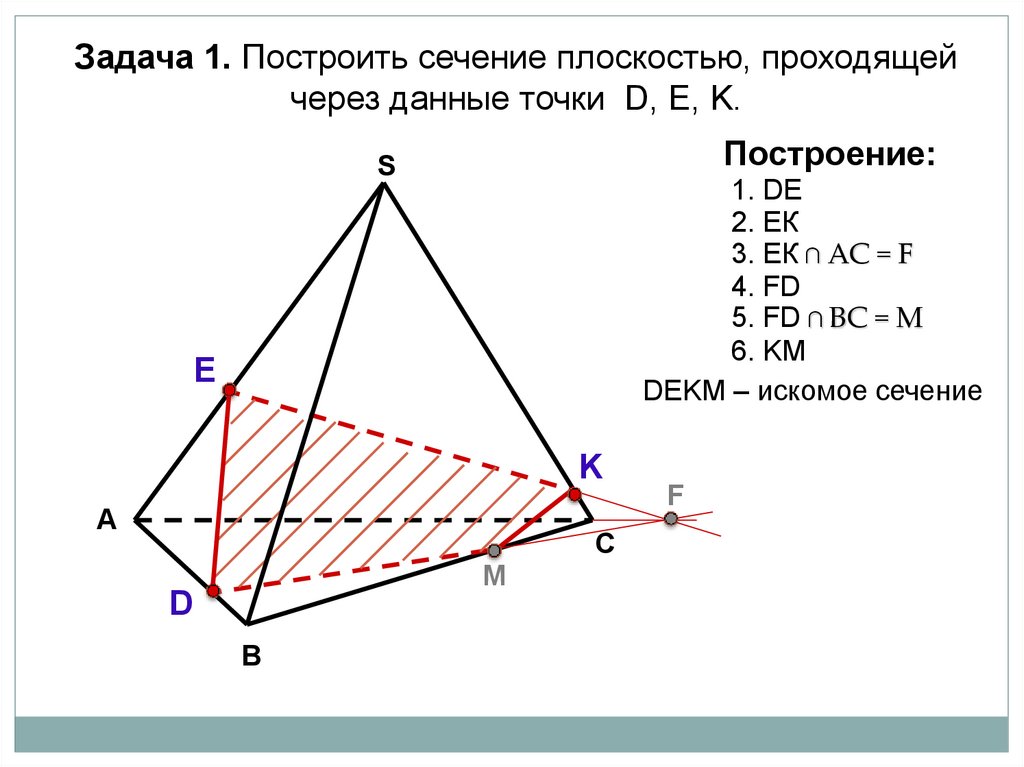
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

11.

Задача 2. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
вАА
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
А1точке
В1В
1С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

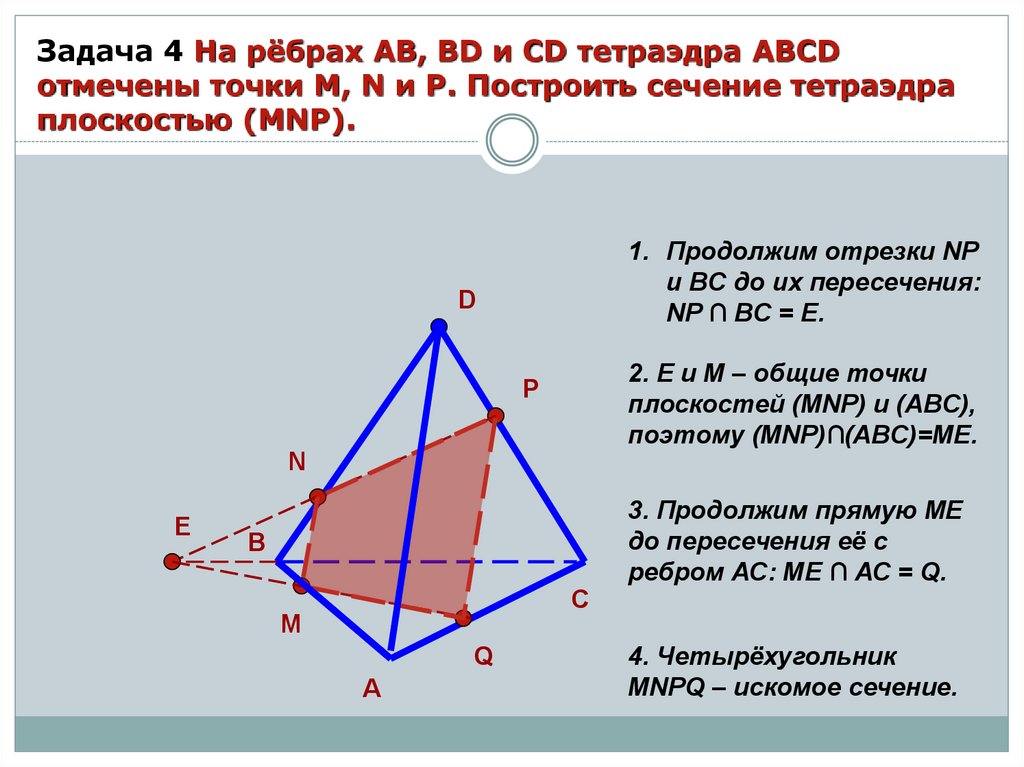
12.

Задача 4 На рёбрах AB, BD и CD тетраэдра ABCD
отмечены точки M, N и P. Построить сечение тетраэдра
плоскостью (MNP).
1. Продолжим отрезки NP
и BC до их пересечения:
NP ∩ BC = E.
D
2. Е и М – общие точки
плоскостей (MNP) и (ABC),
поэтому (MNP)∩(ABC)=МЕ.
P
N
E
B
С
М
Q
А
3. Продолжим прямую МЕ
до пересечения её с
ребром АС: МЕ ∩ АС = Q.
4. Четырёхугольник
MNPQ – искомое сечение.

13.

Задача 5 Точка М лежит на боковой грани АDВ
тетраэдра DАВС. Построить сечение тетраэдра
плоскостью, проходящей через точку М, параллельно
основанию АВС.
D
1. Через точку М проведём
прямую PQ, параллельную
отрезку АВ.
Q
R
2. Через точку Р проводим
прямую PR, параллельную
отрезку АС(Rє DC).
М
Р
В
С
А
3. ΔPQR – искомое сечение.

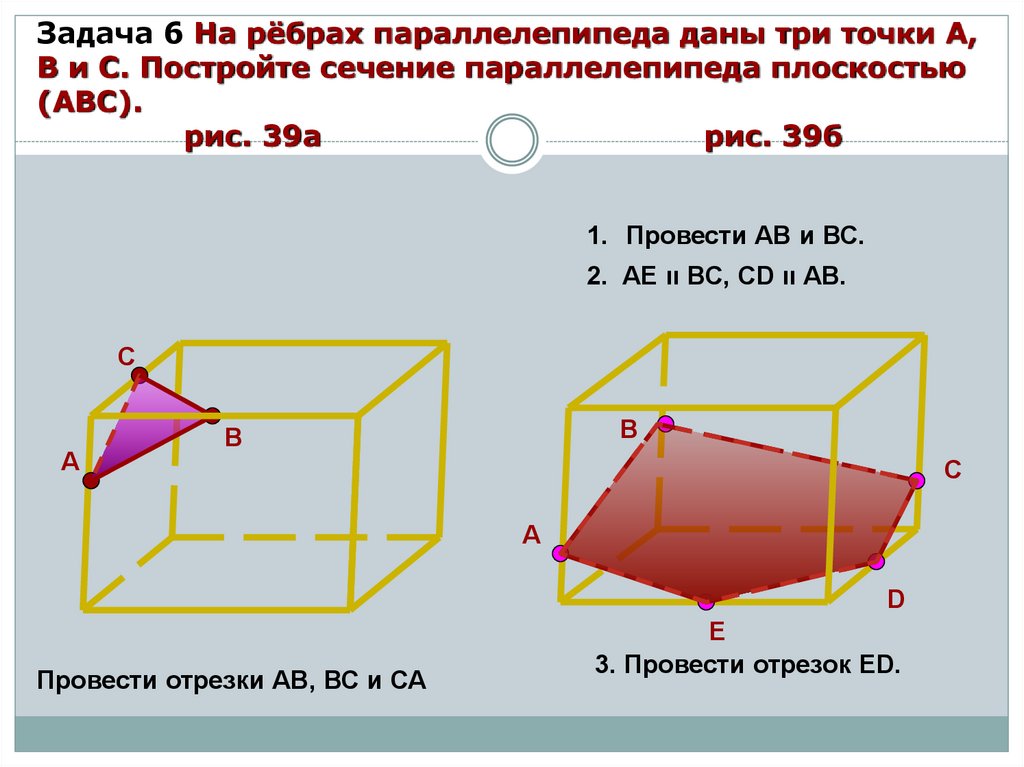
14.

Задача 6 На рёбрах параллелепипеда даны три точки А,
В и С. Постройте сечение параллелепипеда плоскостью
(АВС).
рис. 39а
рис. 39б
1. Провести АВ и ВС.
2. АЕ ıı ВС, СD ıı АВ.
С
А
В
В
С
А
D
Провести отрезки АВ, ВС и СА
E
3. Провести отрезок ЕD.

15.

Задача 7. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

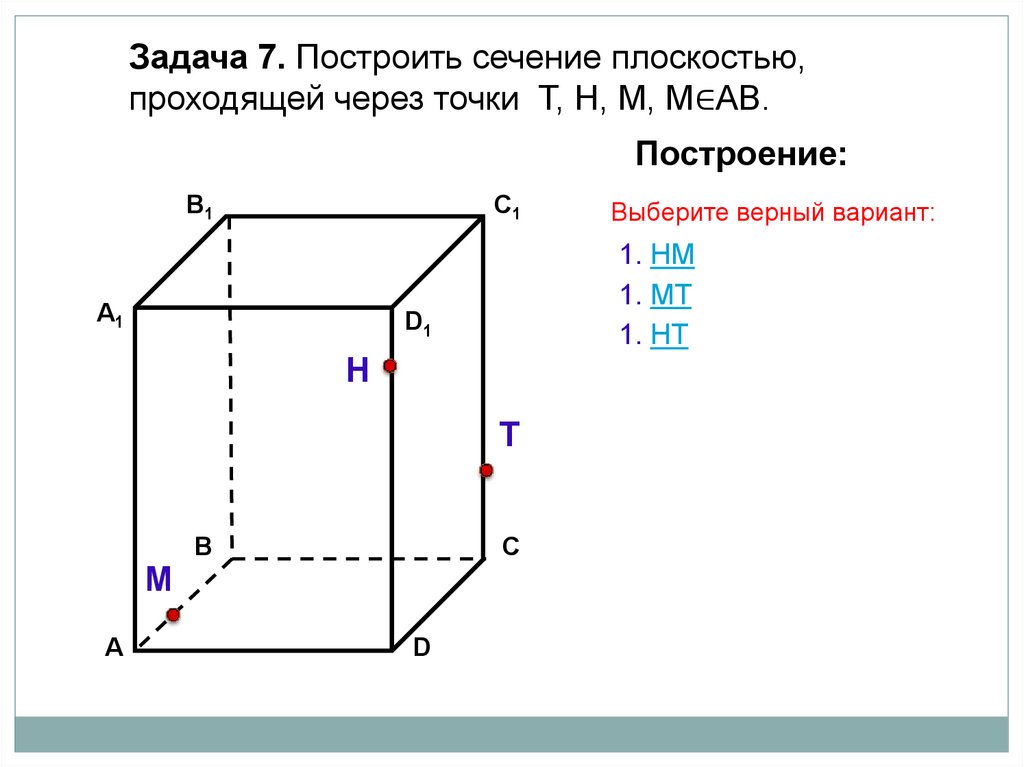
16.

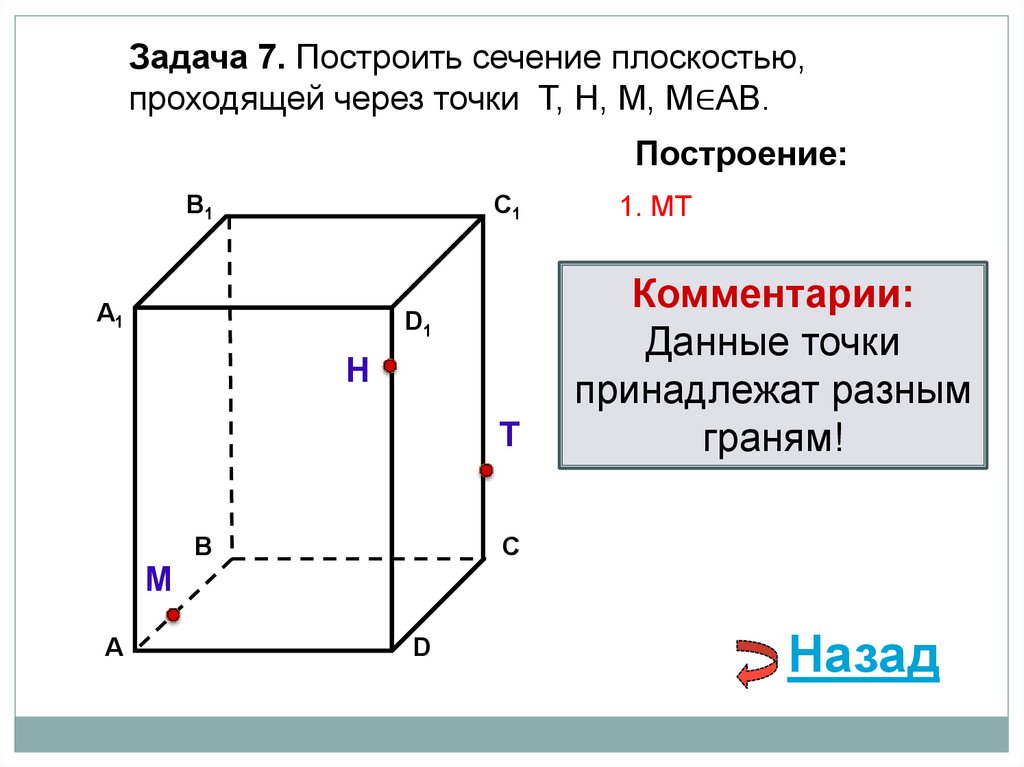
Задача 7. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
Выберите верный вариант:

17.

Задача 7. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

18.

Задача 7. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

19.

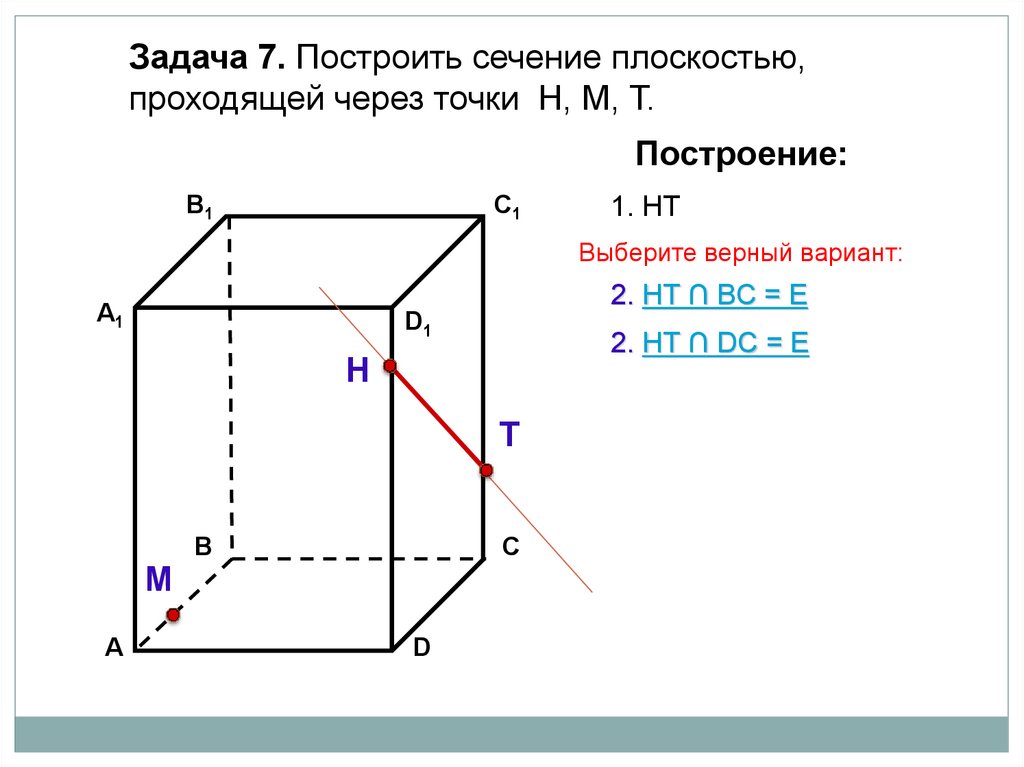
Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D

20.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
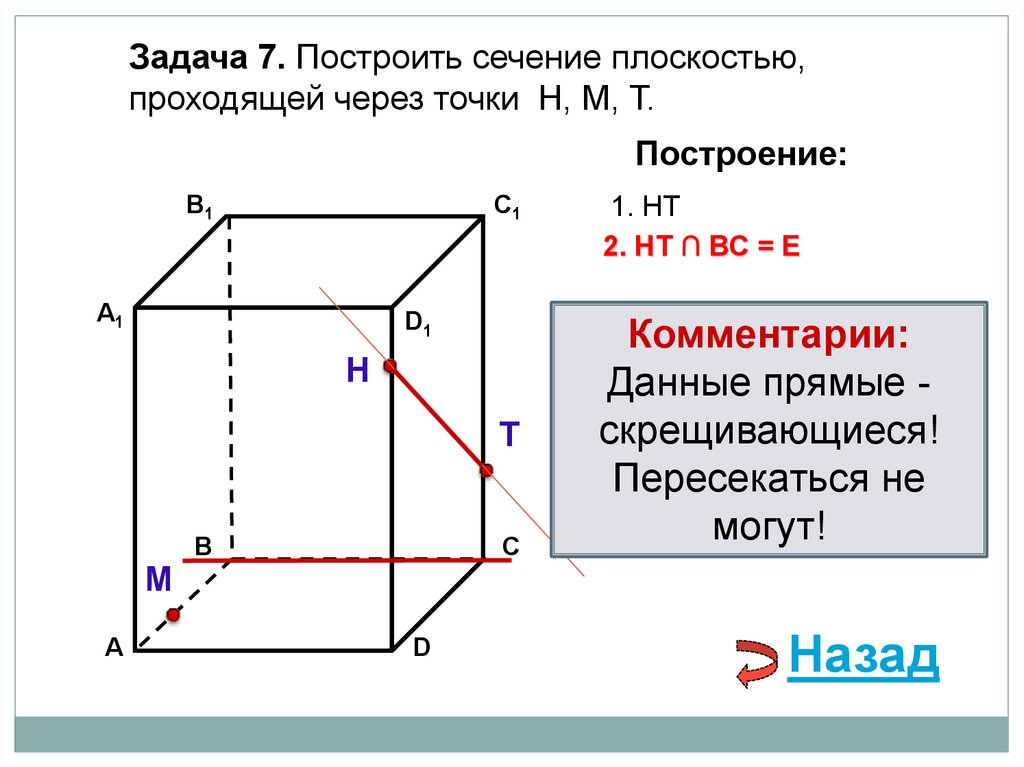
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

21.

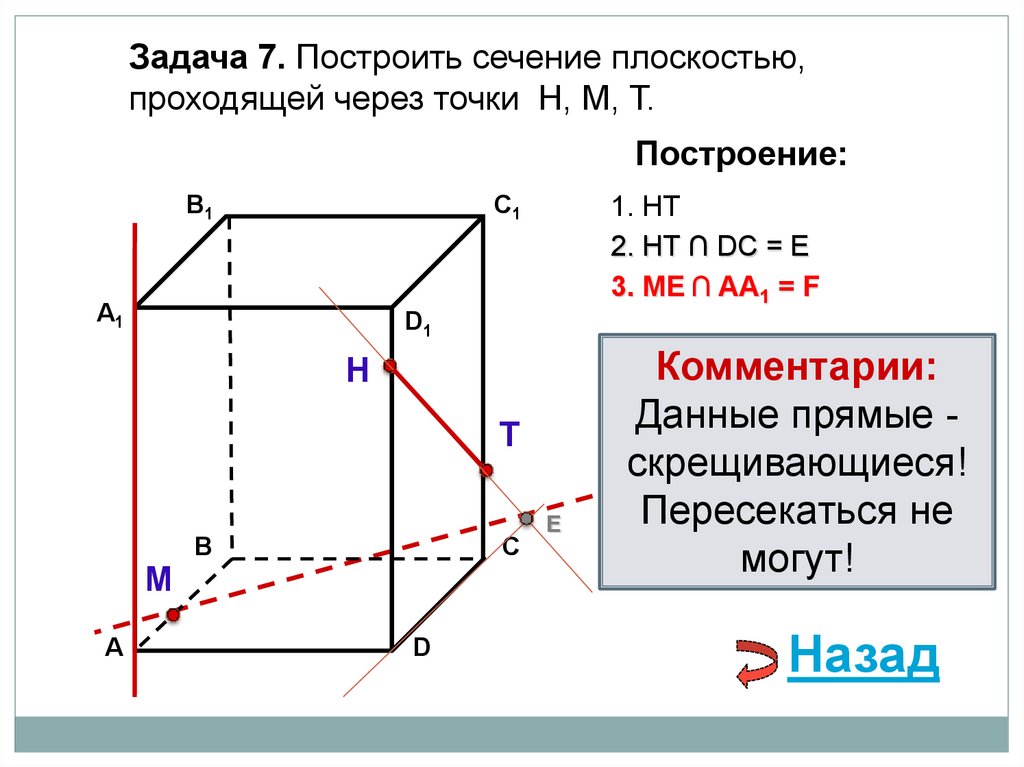
Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
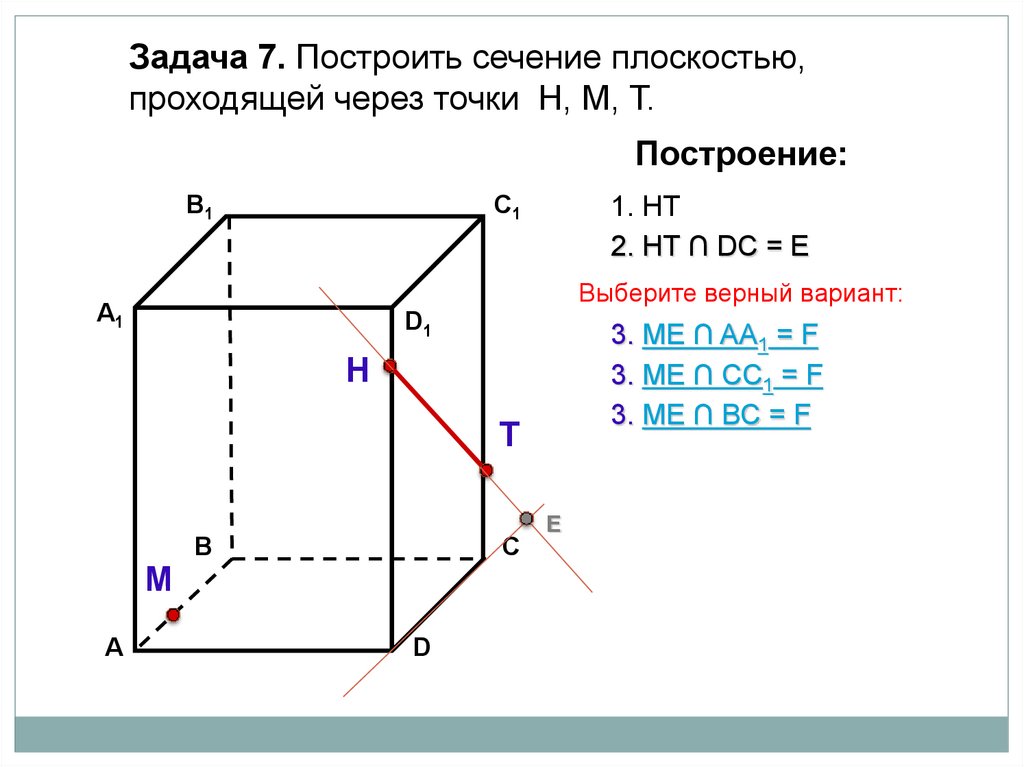
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е

22.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

23.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

24.

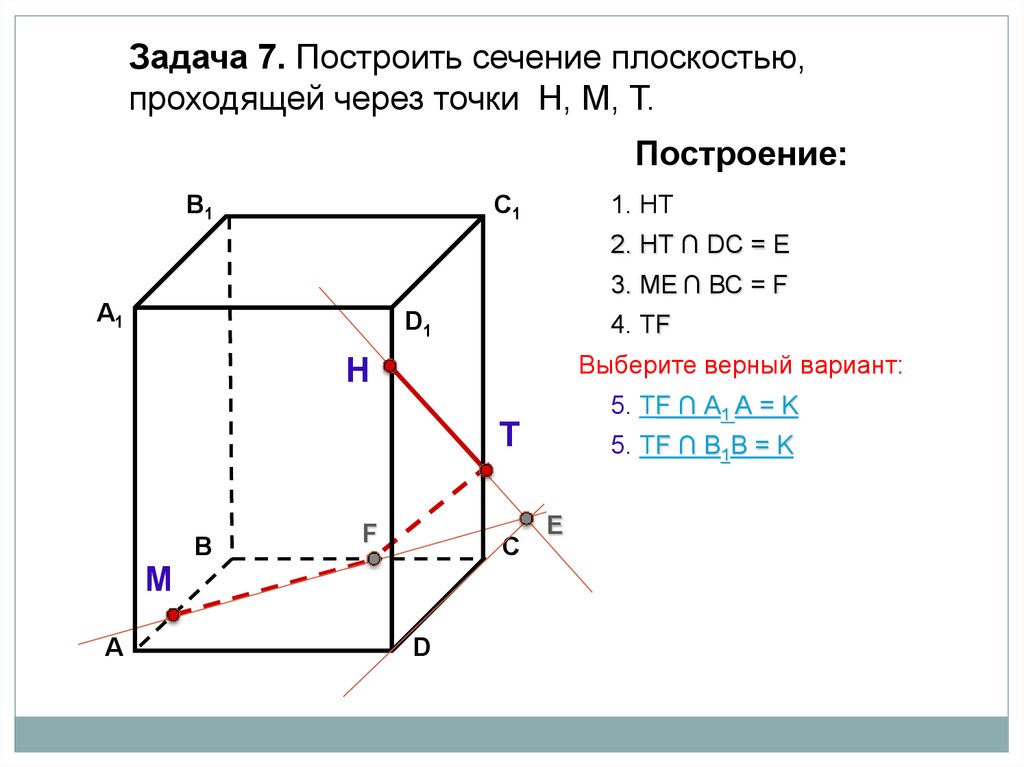
Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
4. НF
Н
4. МТ
Т
М
А
В
F
С
D
4. ТF
E

25.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

26.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

27.

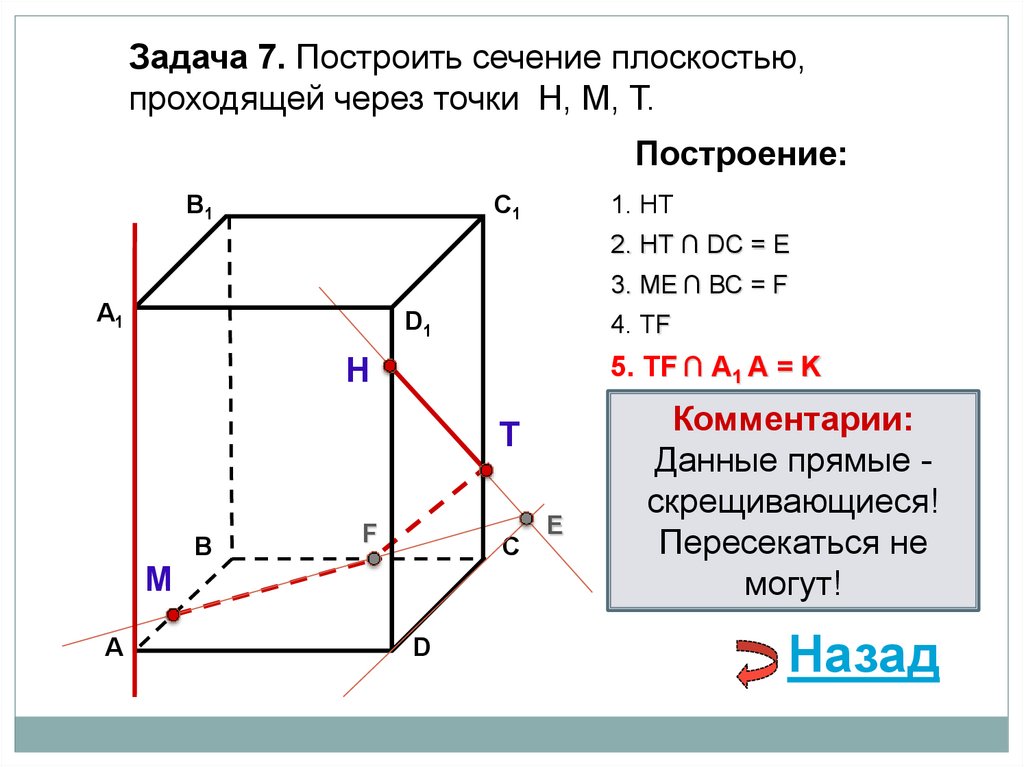
Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А = K
Т
М
А
В
F
С
D
5. ТF ∩ В1В = K
E

28.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

29.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
Выберите верный вариант:
Т
6. НK ∩ АD = L
6. ТK ∩ АD = L
М
F
В
А
С
D
K
E
6. МK ∩ АА1= L

30.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

31.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

32.

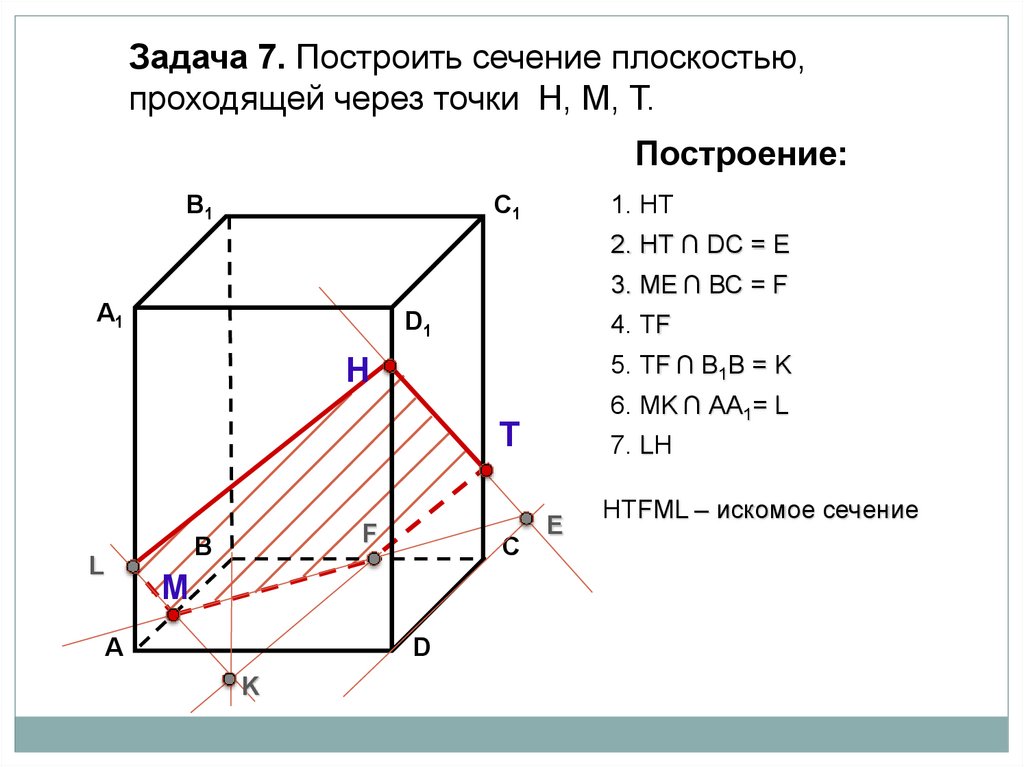
Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
Выберите верный вариант:
7. LF
М
L
F
В
А
С
D
K
E
7. LT
7. LH

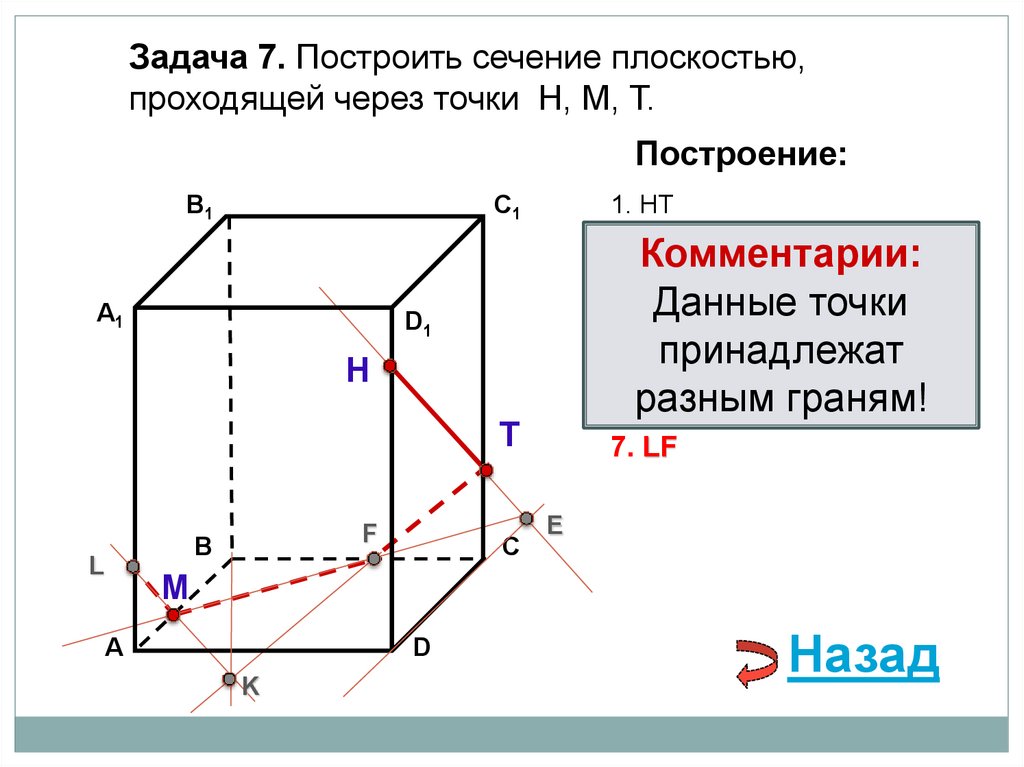
33.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LТ
E
М
А
D
K
Назад

34.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LF
E
М
А
D
K
Назад

35.

Задача 7. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение

36.

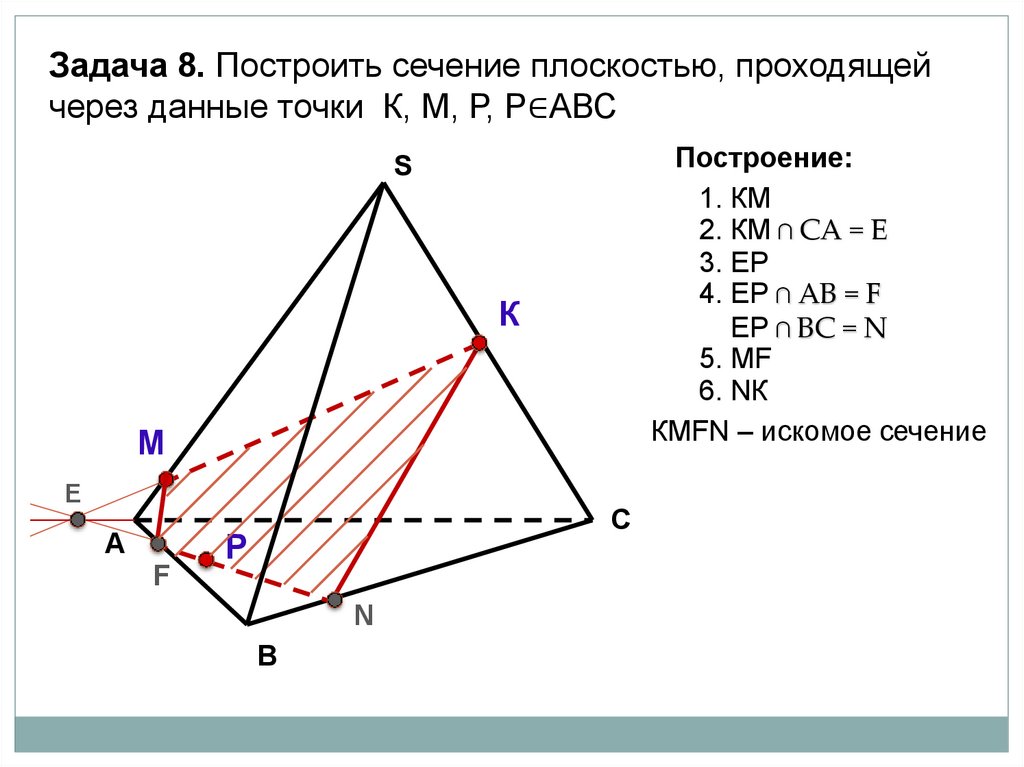
Задача 8. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
S
К
М
А
С
Р
В

37.

Задача 8. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В