Задачи на построение сечений. 10 класс

1.

2.

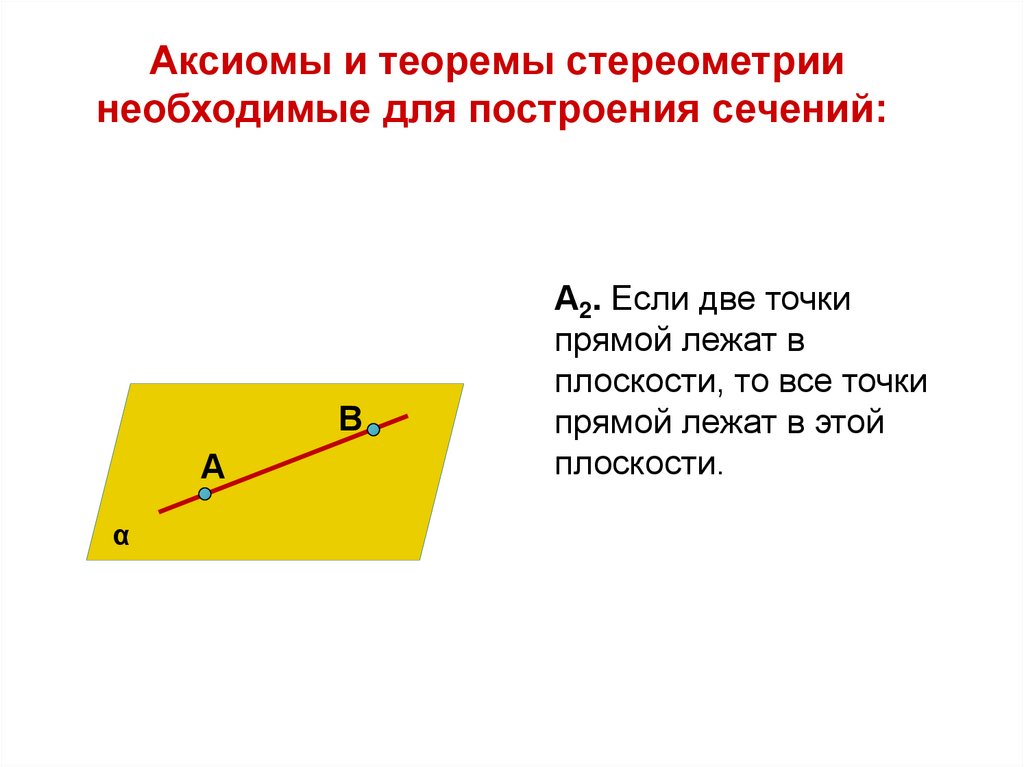
Аксиомы и теоремы стереометрии
необходимые для построения сечений:
В
А
α
А2. Если две точки
прямой лежат в
плоскости, то все точки
прямой лежат в этой
плоскости.

3.

Аксиомы и теоремы стереометрии
необходимые для построения сечений:
β
А
α
a
А3. Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.

4.

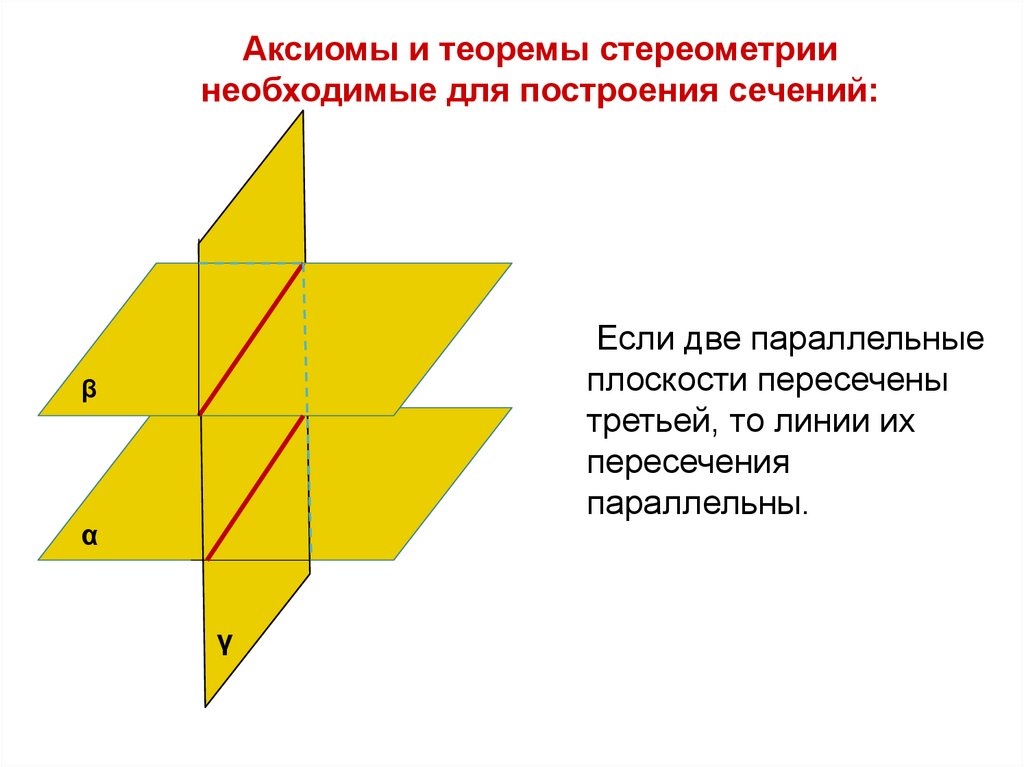
Аксиомы и теоремы стереометрии
необходимые для построения сечений:
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения
параллельны.
β
α
γ

5.

Построить сечение многогранника
плоскостью – это значит указать точки
пересечения секущей плоскости с ребрами
многогранника и соединить эти точки
отрезками, принадлежащими граням
многогранника.
Для построения сечения многогранника
плоскостью нужно в плоскости каждой
грани указать 2 точки, принадлежащие
сечению, соединить их прямой и найти
точки пересечения этой прямой с ребрами
многогранника.

6.

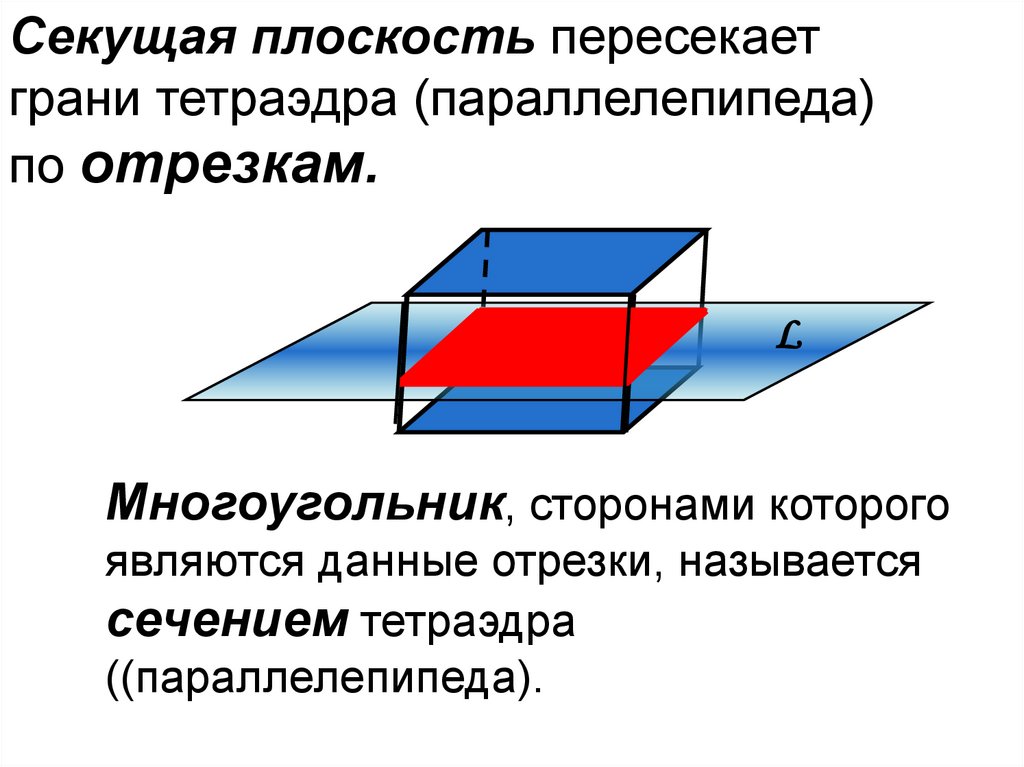
Секущая плоскость пересекает
грани тетраэдра (параллелепипеда)
по отрезкам.
L
Многоугольник, сторонами которого
являются данные отрезки, называется
сечением тетраэдра
((параллелепипеда).

7.

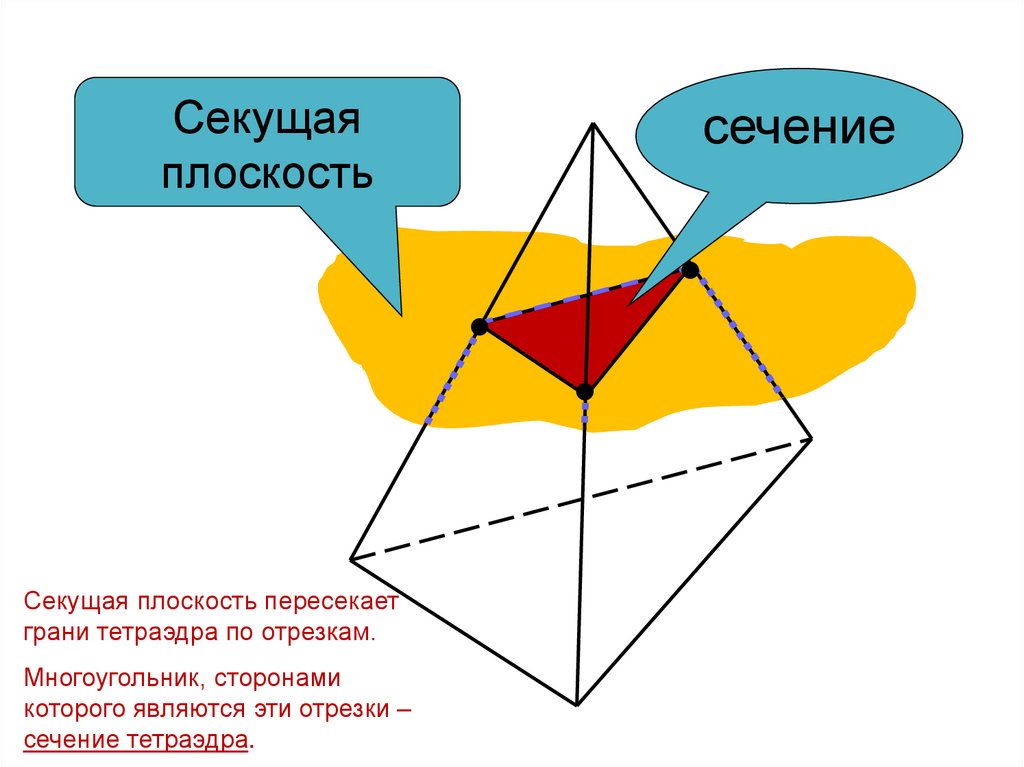
Секущая
плоскость
Секущая плоскость пересекает
грани тетраэдра по отрезкам.
Многоугольник, сторонами
которого являются эти отрезки –
сечение тетраэдра.
сечение

8.

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
параллельные грани по параллельным
отрезкам.
3. Если в плоскости грани отмечена только
одна точка, принадлежащая плоскости
сечения, то надо построить дополнительную
точку. Для этого необходимо найти точки
пересечения уже построенных прямых с
другими прямыми, лежащими в тех же гранях.

9.

Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут
получиться:
Треугольники
Четырехугольники

10.

Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольник
и
Шестиугольники

11.

Блиц - опрос
Задача блиц – опроса:
ответить на вопросы и
обосновать ответ с помощью
аксиом, теорем и свойств
параллельных плоскостей.

12.

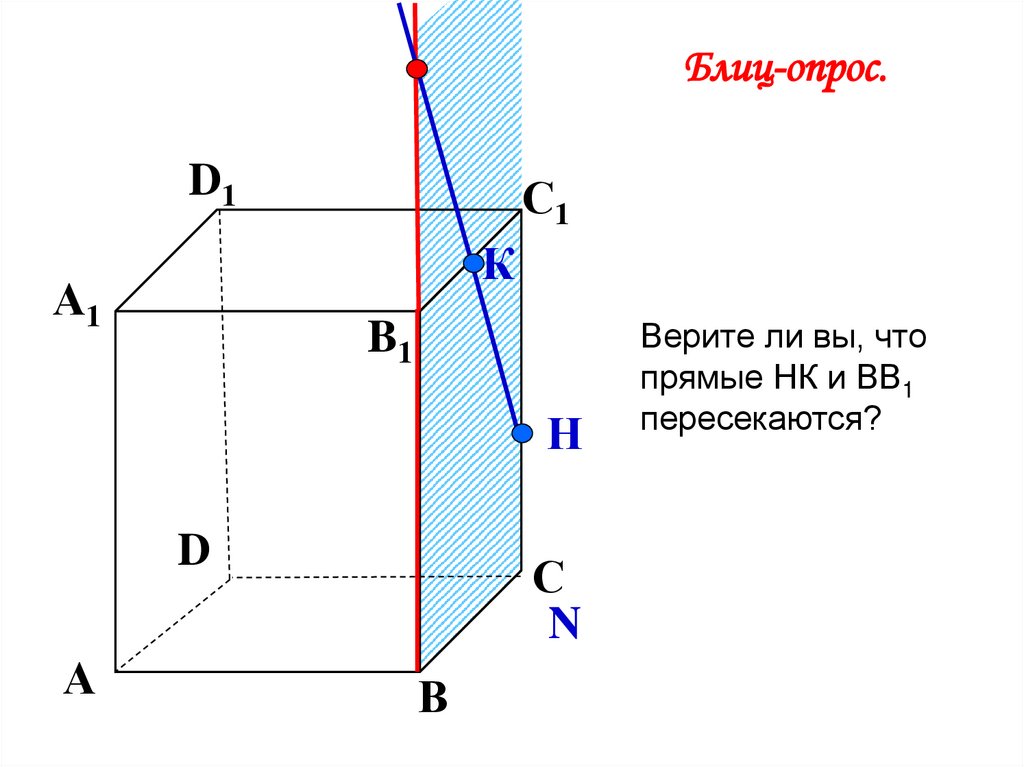
Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые
НК и ВВ1 пересекаются?
B1
D
А
H
С
В

13.

Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

14.

Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
Верите ли вы, что прямые
НК и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

15.

Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

16.

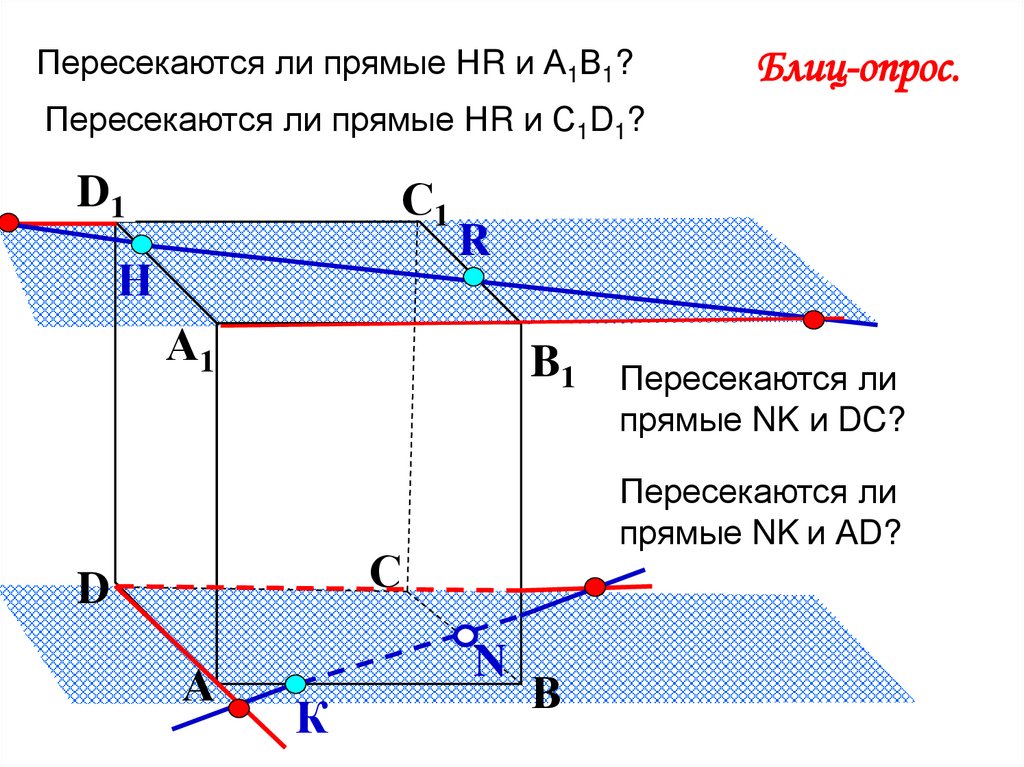
Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

17.

Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

18.

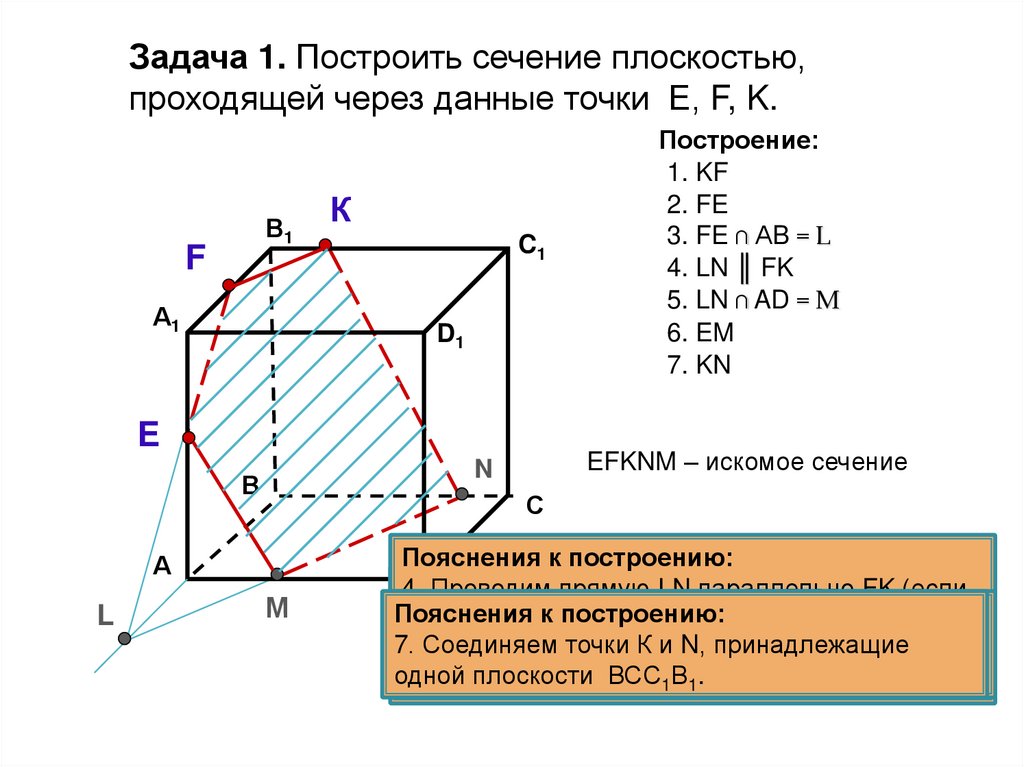
Задача 1. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
Построение:
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
вАА
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
А1точке
В1В
1С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

19.

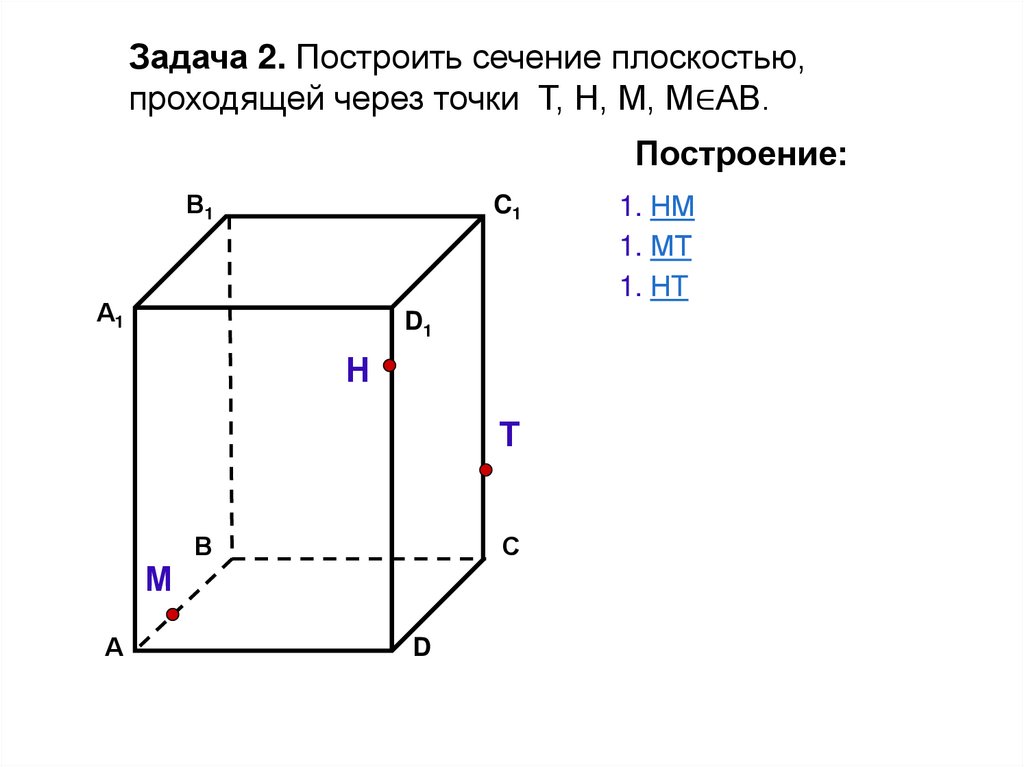
Задача 2. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НМ
1. МТ
1. НT

20.

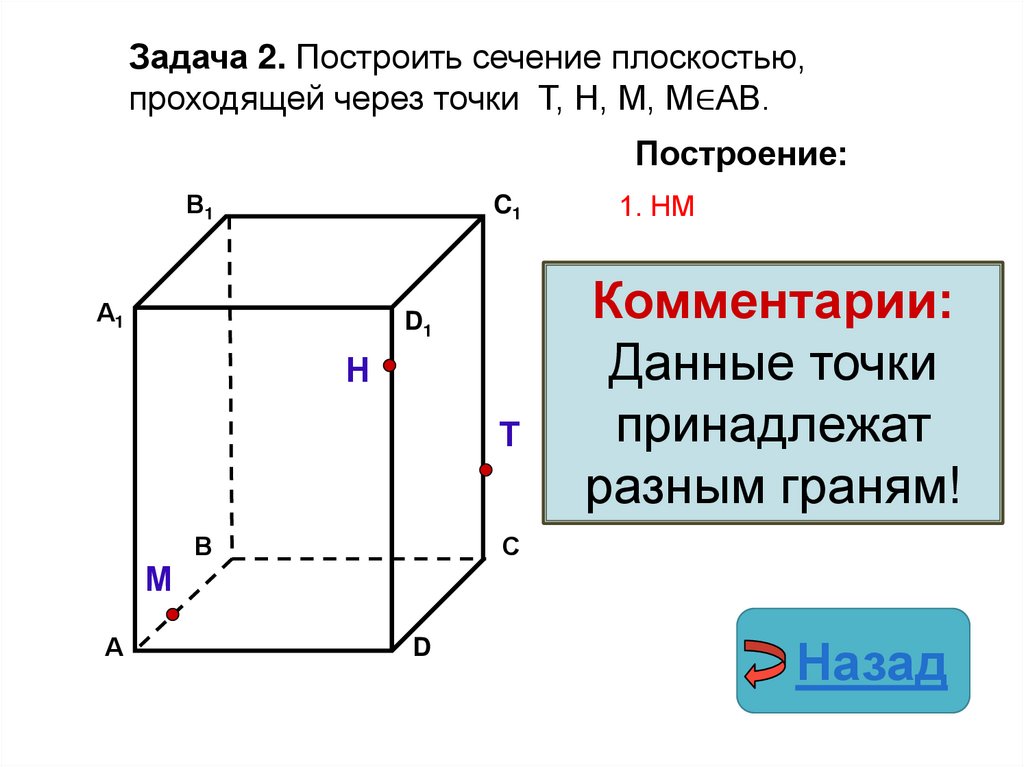
Задача 2. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат
разным граням!
С
D
Назад

21.

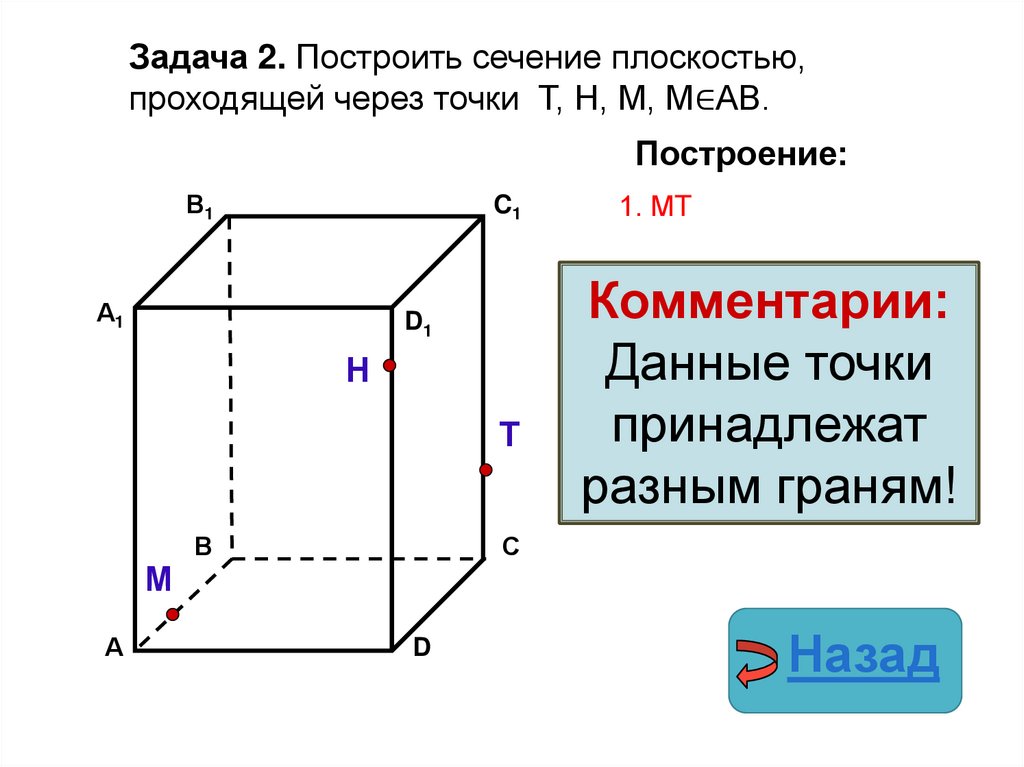
Задача 2. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат
разным граням!
С
D
Назад

22.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = О1
2. НТ ∩ DС = О1

23.

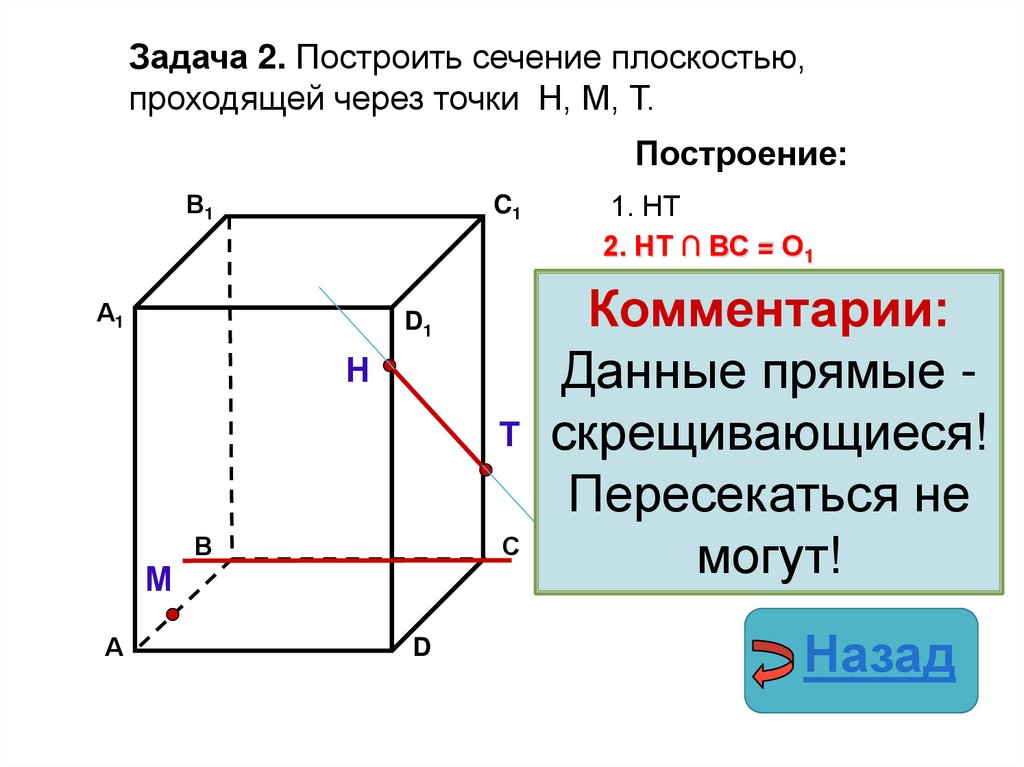
Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
М
А
В
D
1. НТ
2. НТ ∩ ВС = О1
Комментарии:
Данные прямые Т скрещивающиеся!
Пересекаться не
С
могут!
Назад

24.

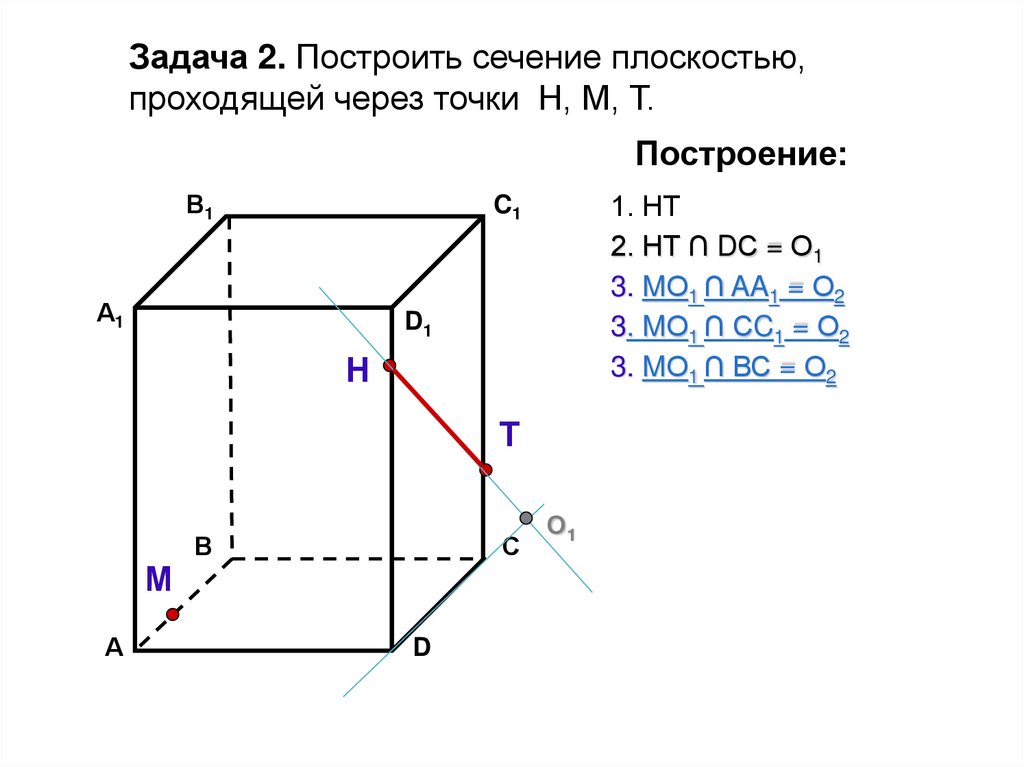
Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = О1
3. MО1 ∩ AA1 = О2
3. MО1 ∩ СC1 = О2
3. MО1 ∩ ВС = О2
C1
А1
D1
Н
Т
М
А
В
С
D
О1

25.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = О1
3. MО1 ∩ AA1 = О2
C1
А1
D1
Н
Т
М
А
В
С
D
О1
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

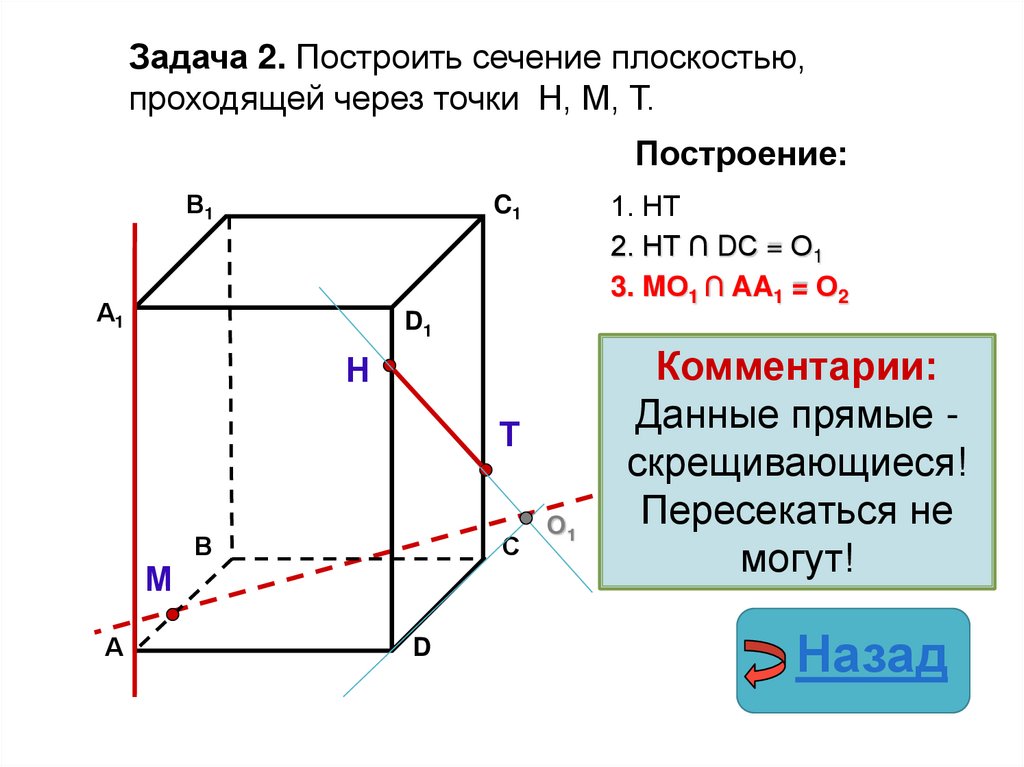
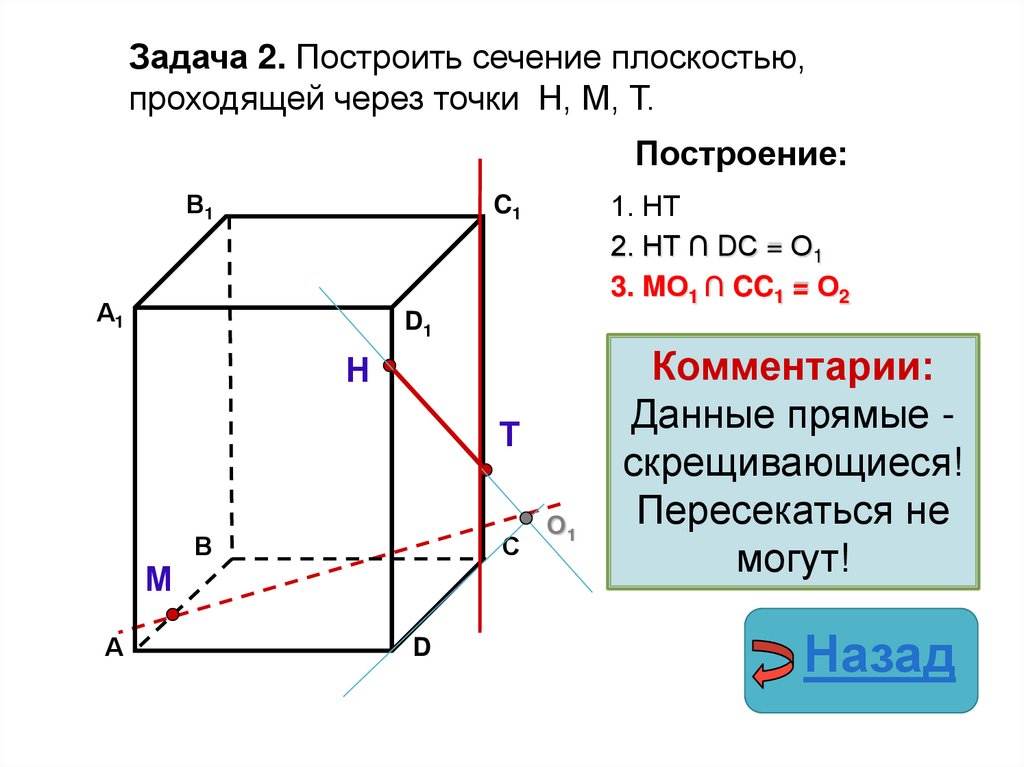
26.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = О1
3. MО1 ∩ CC1 = О2
C1
А1
D1
Н
Т
М
А
В
С
D
О1
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

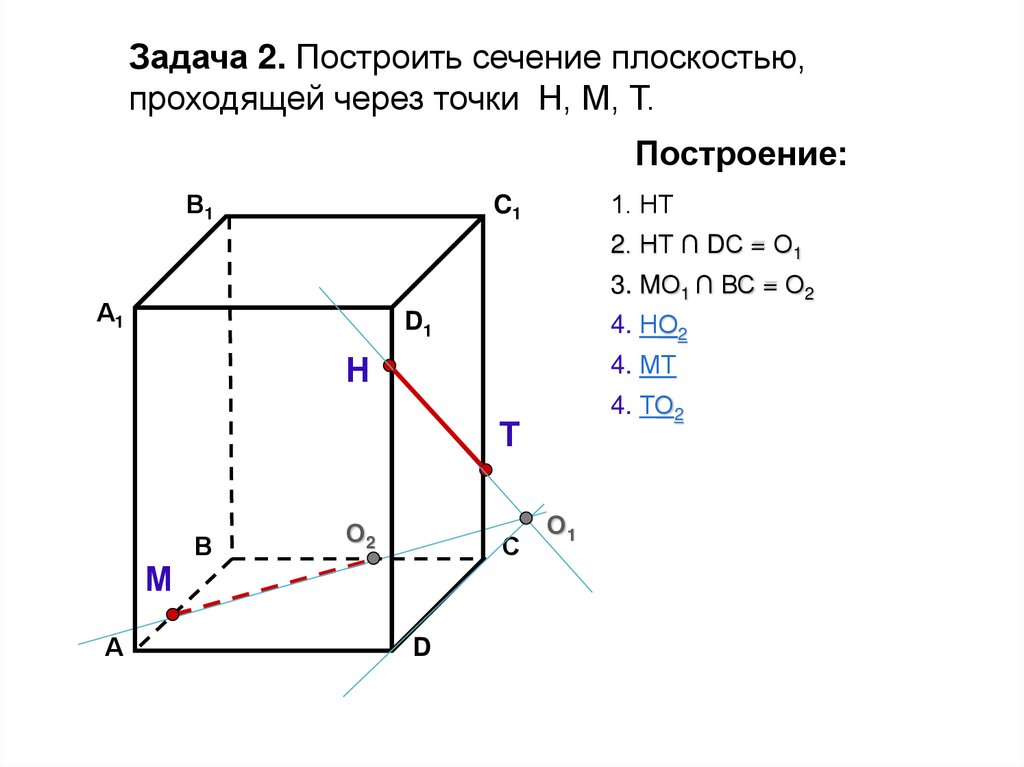
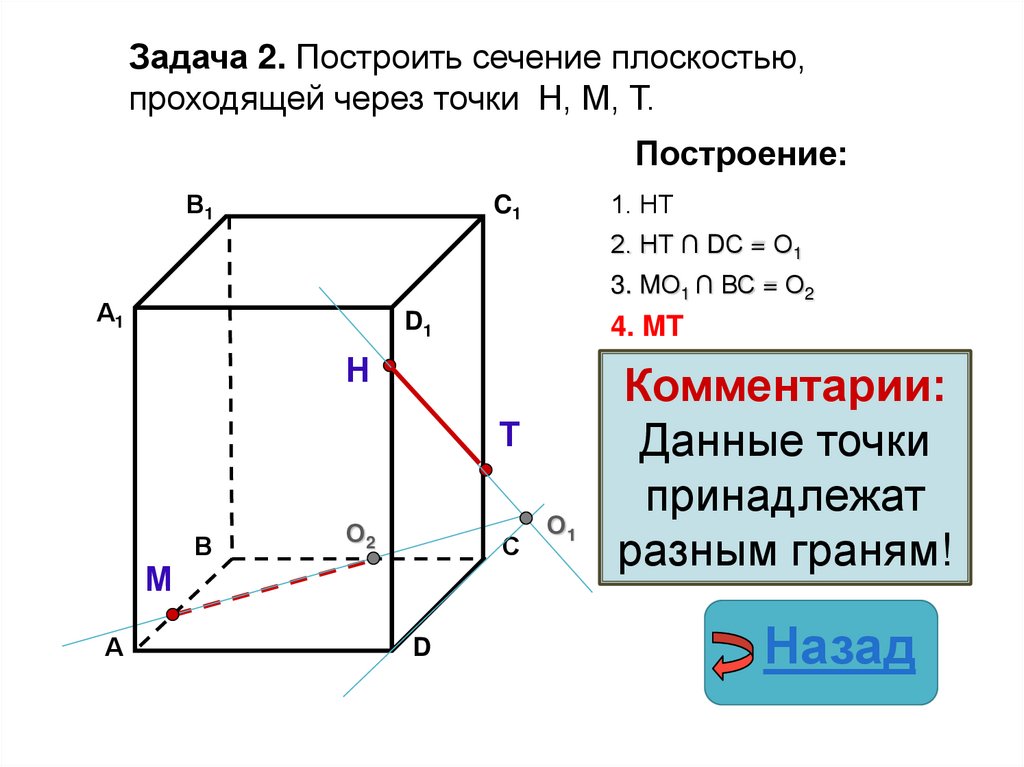
27.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. НО2
D1
4. МТ
Н
4. ТО2
Т
М
А
В
О2
С
D
О1

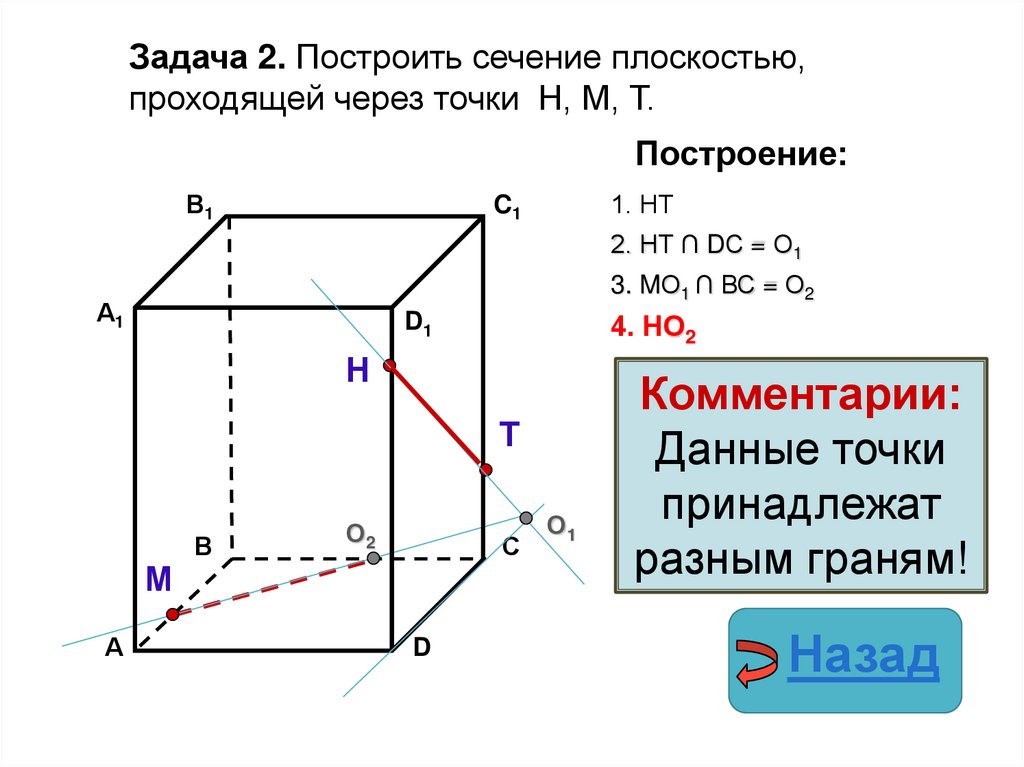
28.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. НО2
D1
Н
Т
М
А
В
О2
С
D
О1
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

29.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
D1
4. MT
Н
Т
М
А
В
О2
С
D
О1
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

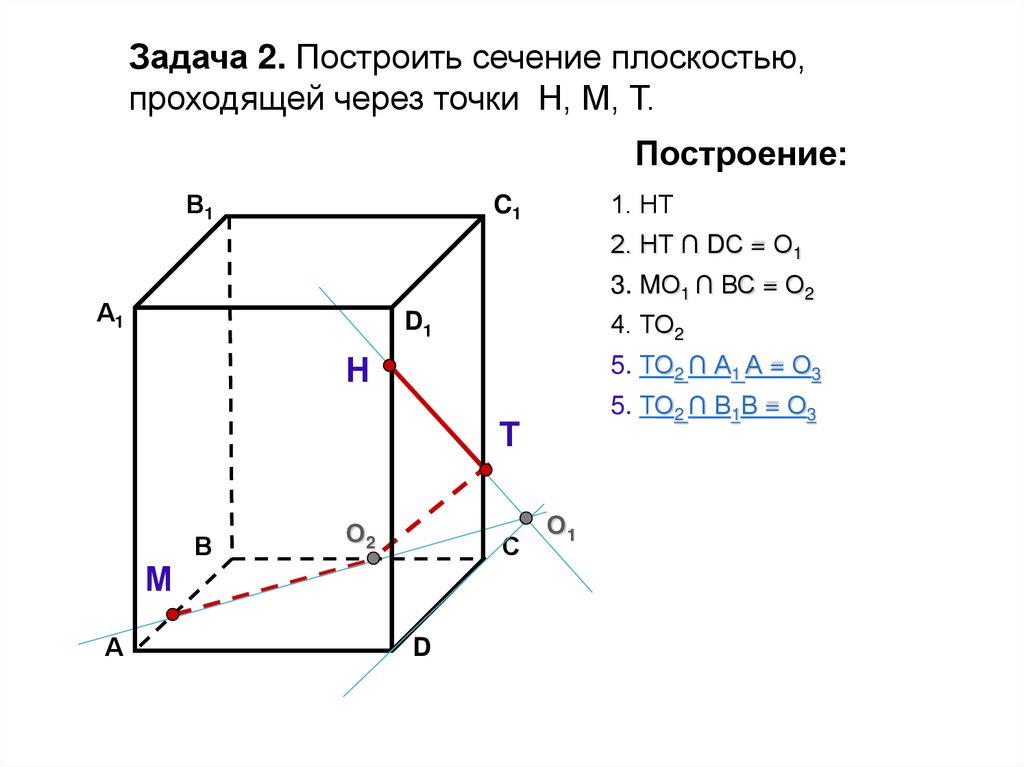
30.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. ТО2
D1
5. ТО2 ∩ А1 А = О3
Н
5. ТО2 ∩ В1В = О3
Т
М
А
В
О2
С
D
О1

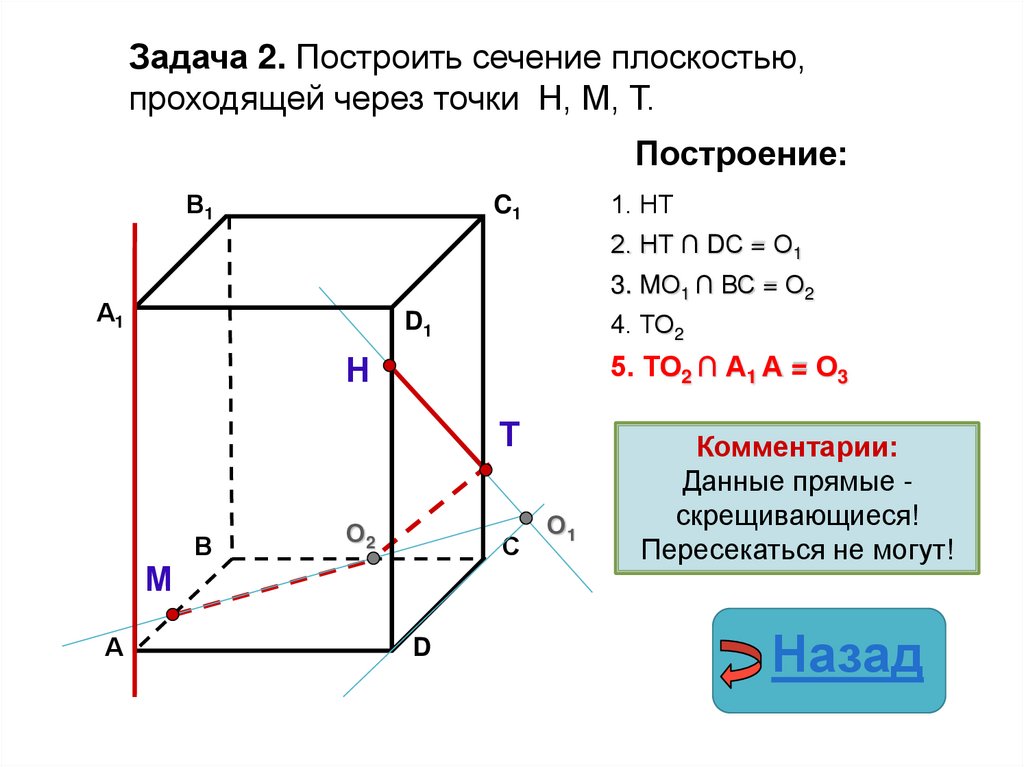
31.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. ТО2
D1
5. ТО2 ∩ А1 А = О3
Н
Т
М
А
В
О2
С
D
О1
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не могут!
Назад

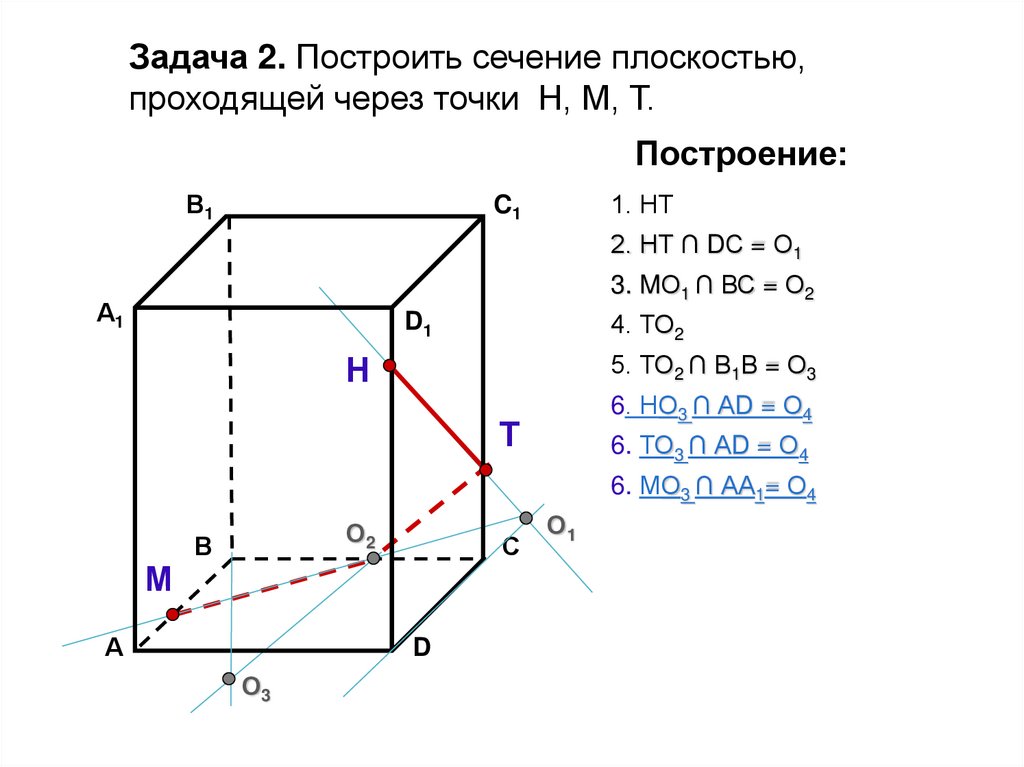
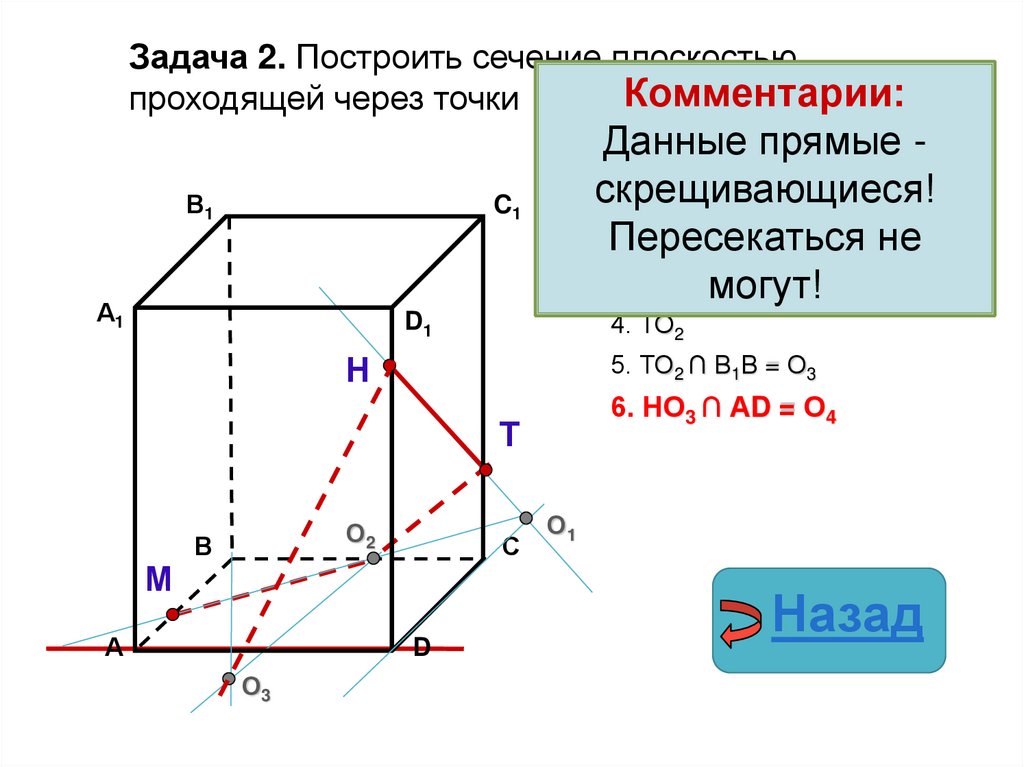
32.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. ТО2
D1
5. ТО2 ∩ В1В = О3
Н
6. НО3 ∩ АD = О4
Т
6. ТО3 ∩ АD = О4
6. МО3 ∩ АА1= О4
М
О2
В
А
С
D
О3
О1

33.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Комментарии:
Т.
В1
Данные
прямые Построение:
скрещивающиеся!
1. НТ
Пересекаться
не
2. НТ ∩ DС = О1
3. MО1 ∩могут!
ВС = О2
C1
А1
4. ТО2
D1
5. ТО2 ∩ В1В = О3
Н
6. НО3 ∩ АD = О4
Т
М
О2
В
А
С
D
О3
О1
Назад

34.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Комментарии:
Т.
В1
Данные
прямые Построение:
скрещивающиеся!
1. НТ
Пересекаться
не
2.
НТ ∩ DС = О1
3. MО1 ∩могут!
ВС = О2
C1
А1
4. ТО2
D1
5. ТО2 ∩ В1В = О3
Н
6. TО3 ∩ АD = О4
Т
М
О2
В
А
С
D
О3
О1
Назад

35.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. ТО2
D1
5. ТО2 ∩ В1В = О3
Н
6. МО3 ∩ АА1= О4
Т
7. О4Т
7. О4О2
О4
М
О2
В
А
С
D
О3
О1
7. О4Н

36.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
Комментарии:
1. НТ
Данные
2. НТ ∩ DС = О точки
3. MО ∩ ВС = О
принадлежат
4. ТО
5. ТО ∩ В В =граням!
О
разным
C1
1
1
А1
D1
2
Н
2
О4
В
С
М
А
D
О3
1
3
6. МО3 ∩ АА1= О4
Т
О2
2
7. О4Т
О1
Назад

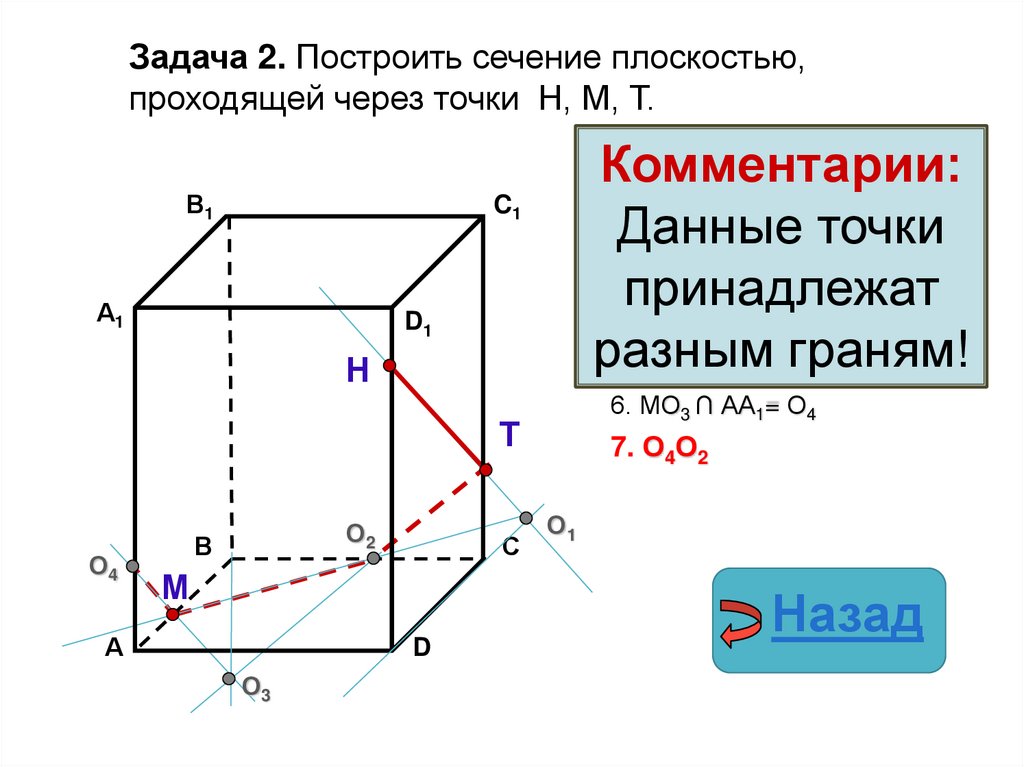
37.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
Комментарии:
1. НТ
Данные
2.
НТ ∩ DС = О точки
3.принадлежат
MО ∩ ВС = О
4. ТО
разным
граням!
5. ТО ∩ В В = О
C1
1
1
А1
D1
2
Н
2
О4
В
С
М
А
D
О3
1
3
6. МО3 ∩ АА1= О4
Т
О2
2
7. О4О2
О1
Назад

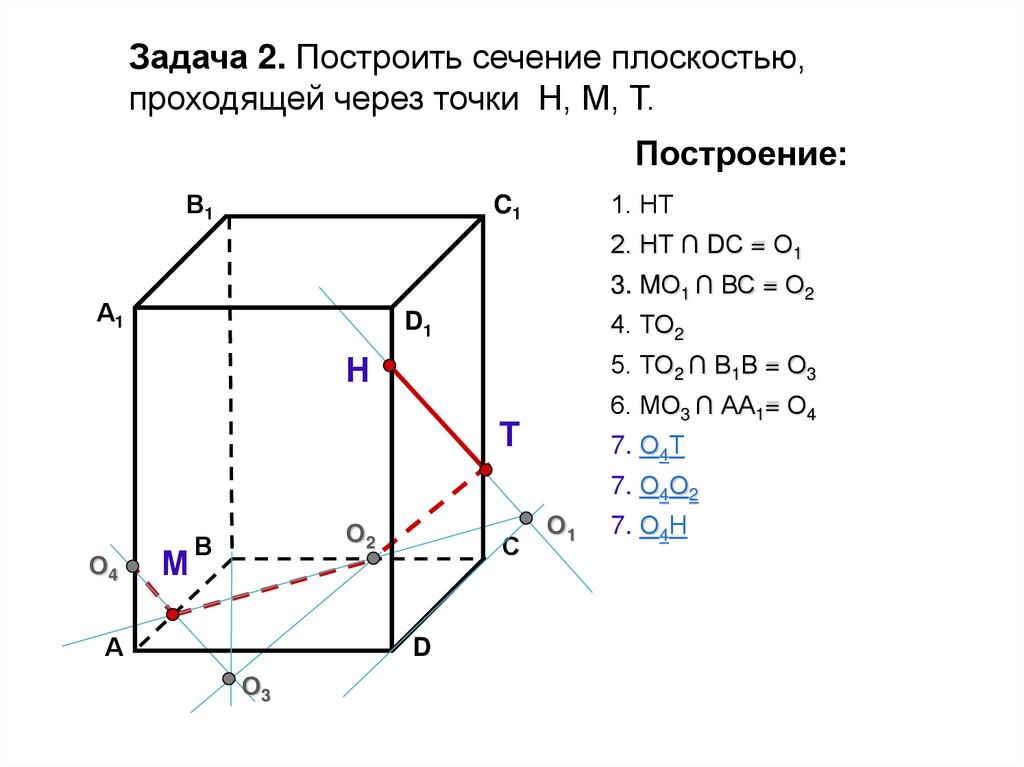
38.

Задача 2. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = О1
3. MО1 ∩ ВС = О2
А1
4. ТО2
D1
5. ТО2 ∩ В1В = О3
Н
6. МО3 ∩ АА1= О4
Т
О4
О2
В
С
М
А
D
О3
7. О4Н
О1
НТО2МО4 – искомое сечение

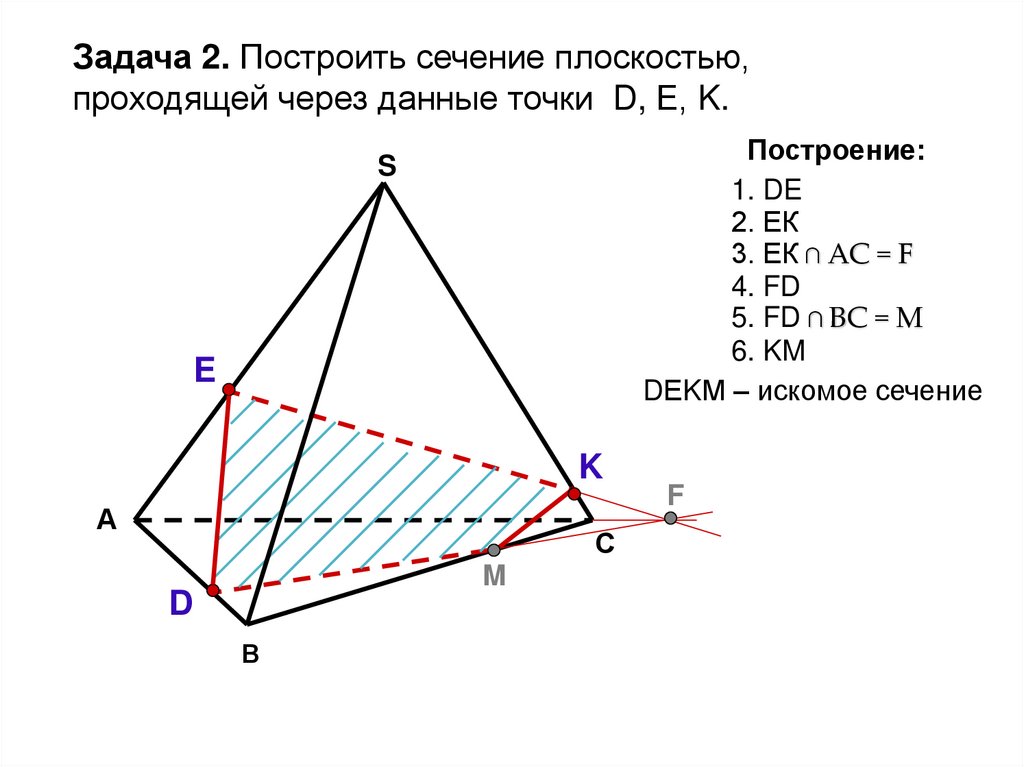
39.

Задача 2. Построить сечение плоскостью,
проходящей через данные точки D, Е, K.
Построение:
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
S
E
K
А
С
M
D
В
F

40.

Задача 4. Построить сечение плоскостью,
проходящей через точки Р, К, М, М∈ВС.
Построение:
В1
К
А1
C1
Р
D1
N
М
В
А
С
Р1
E
К1
D
1. КP
2. EM ║ КP (К1Р1)
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение

41.

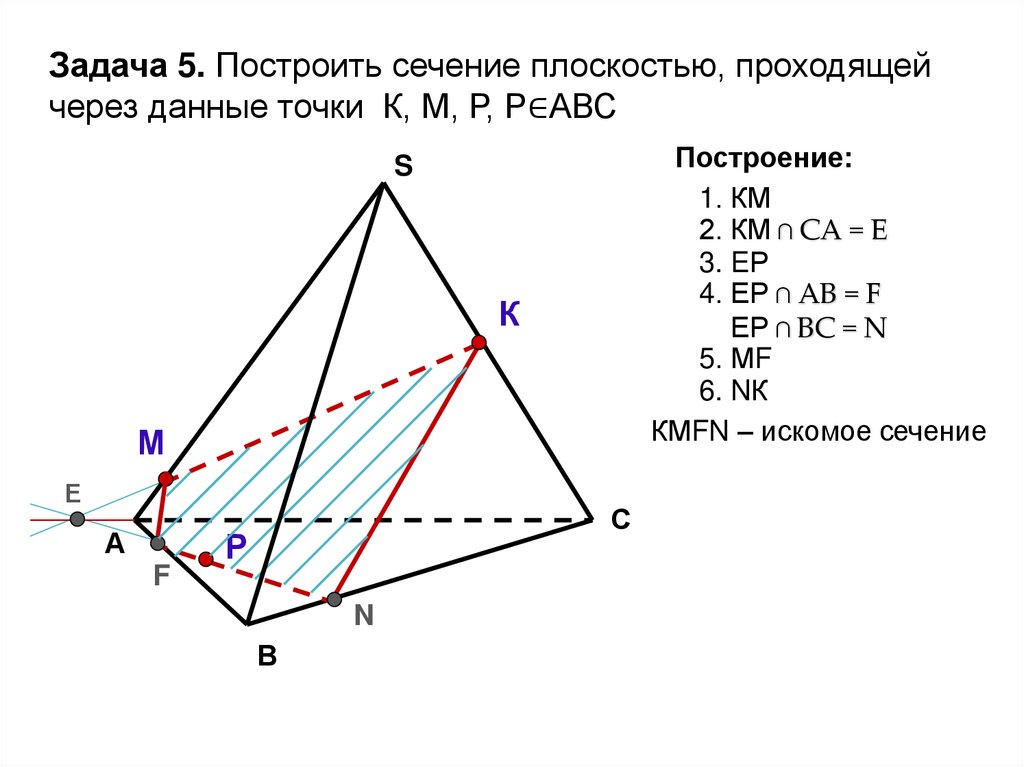
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В

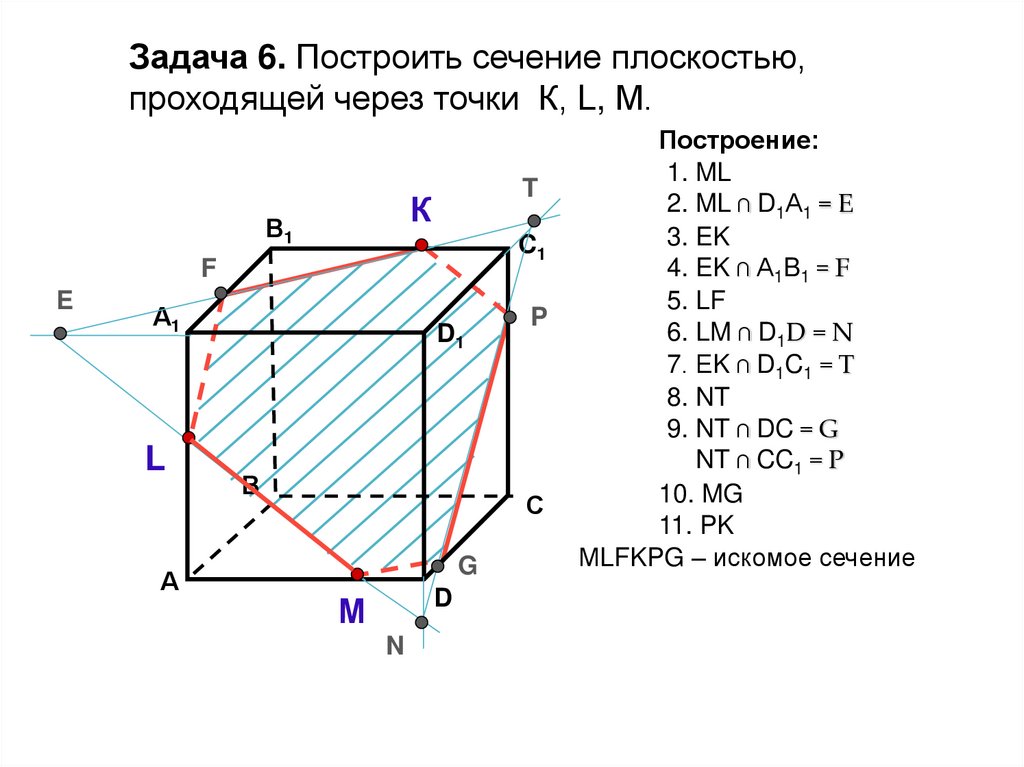
42.

Задача 6. Построить сечение плоскостью,
проходящей через точки К, L, М.
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
Построение:
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

43.

Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
В1
К
А1
C1
D1
L
В
С
А
F
D

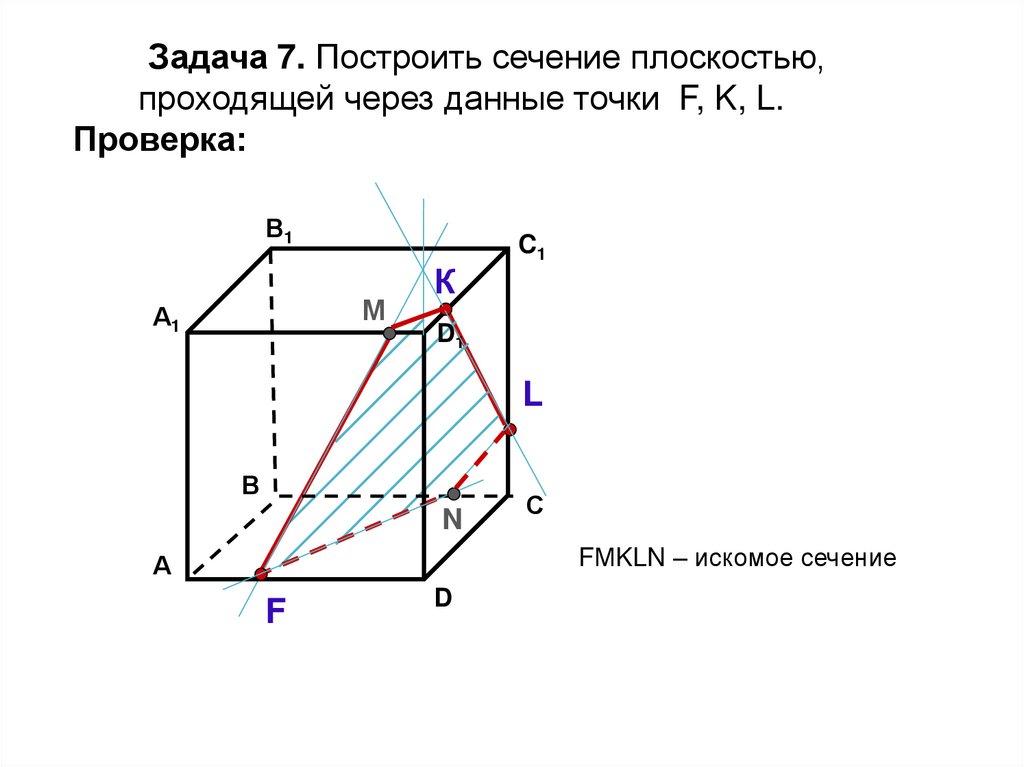
44.

Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
Проверка:
В1
М
А1
К
C1
D1
L
В
N
С
FМKLN – искомое сечение
А
F
D

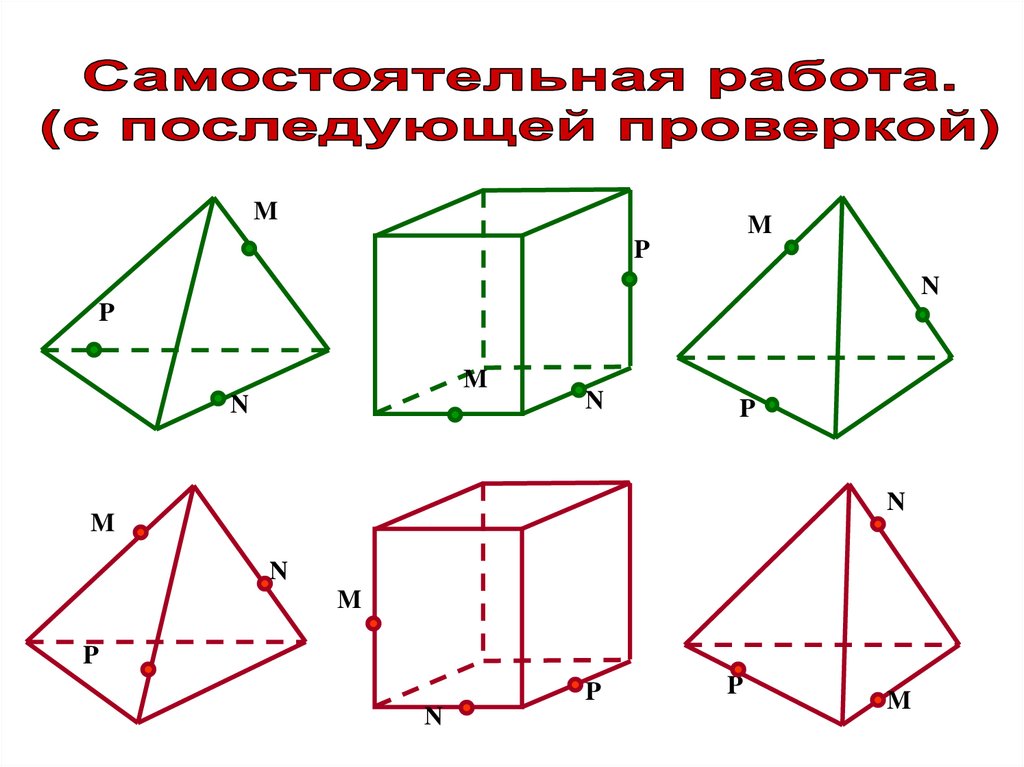
45.

M
M
P
N
P
M
N
N
P
N
M
N
M
P
P
N
P
M

46.

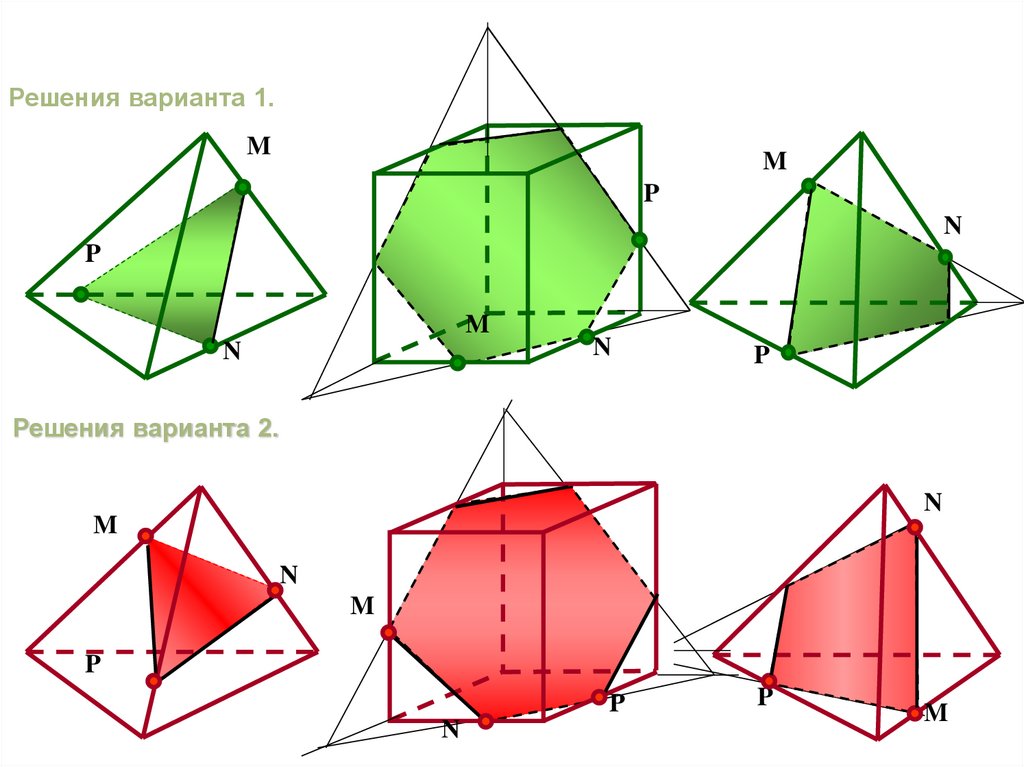
Решения варианта 1.
M
M
P
N
P
M
N
N
P
Решения варианта 2.
N
M
N
M
P
P
N
P
M