Похожие презентации:
Система обучения алгебре и началам математического анализа, направленная на формирование готовности к прохождению ЕГЭ
1.
СИСТЕМА ОБУЧЕНИЯ АЛГЕБРЕ И НАЧАЛАММАТЕМАТИЧЕСКОГО АНАЛИЗА, НАПРАВЛЕННАЯ НА
ФОРМИРОВАНИЕ ГОТОВНОСТИ У ОБУЧАЮЩИХСЯ К
ПРОХОЖДЕНИЮ ИТОГОВОЙ АТТЕСТАЦИИ (ЕГЭ)
Все права защищены. Никакая часть презентации не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в Интернете и в
корпоративных сетях, а также запись в память ЭВМ, для частного или публичного использования, без письменного разрешения владельца авторских прав. © АО «Издательство «Просвещение», 2021 г.
2.
Приказ № 766 от 23.12.2020О внесении изменений в федеральный перечень учебников, допущенных к использованию при
реализации имеющих государственную аккредитацию образовательных программ начального
общего, основного общего, среднего общего образования организациями, осуществляющими
образовательную деятельность, утверждённый приказом Министерства просвещения Российской
Федерации от 20.05.2020 г. № 254
1.1.2.4.1.11.1 Математика
1.1.2.4.1.11.2
Истомина Н.Б.,
Горина О.П.,
Тихонова Н.Б.
5 АО «Издательство
6 «Просвещение»
1.1.2.4.2.13.1 Алгебра
1.1.2.4.2.13.2
1.1.2.4.2.13.3
Мордкович А.Г.,
Семенов П.В.,
Александрова Л.А.,
Мардахаева Е.Л.
Мордкович А.Г.,
Семенов П.В.,
Александрова Л.А.,
Мардахаева Е.Л.
7 ООО «БИНОМ.
8 Лаборатория знаний»; АО
9 «Издательство
«Просвещение»
10 АО «Издательство
11 «Просвещение»
1.1.3.4.1.25.1 Математика: алгебра и начала
1.1.3.4.1.25.2 математического анализа,
геометрия. Алгебра и начала
математического анализа
Конобеева Т.А.,
Бондаренко Р.А.,
Кожанова А.П.,
Павлова Л.А.
До 1 июля
2025 года
От 20 мая
2020 года
№ 254
Польшакова О.Е.,
Еремченко И.А.,
Кожанова А.П.,
Кочагина М.Н.
До 28
июня
2025 года
3.
Вопросы для обсуждения1. Концептуальные идеи построения курса алгебры.
2. Эффективные приёмы повторения и систематизации
теоретического материала.
3. Примеры применения теоретических знаний на
практике.
4.
1. Концептуальные идеи построения курсаалгебры.
5.
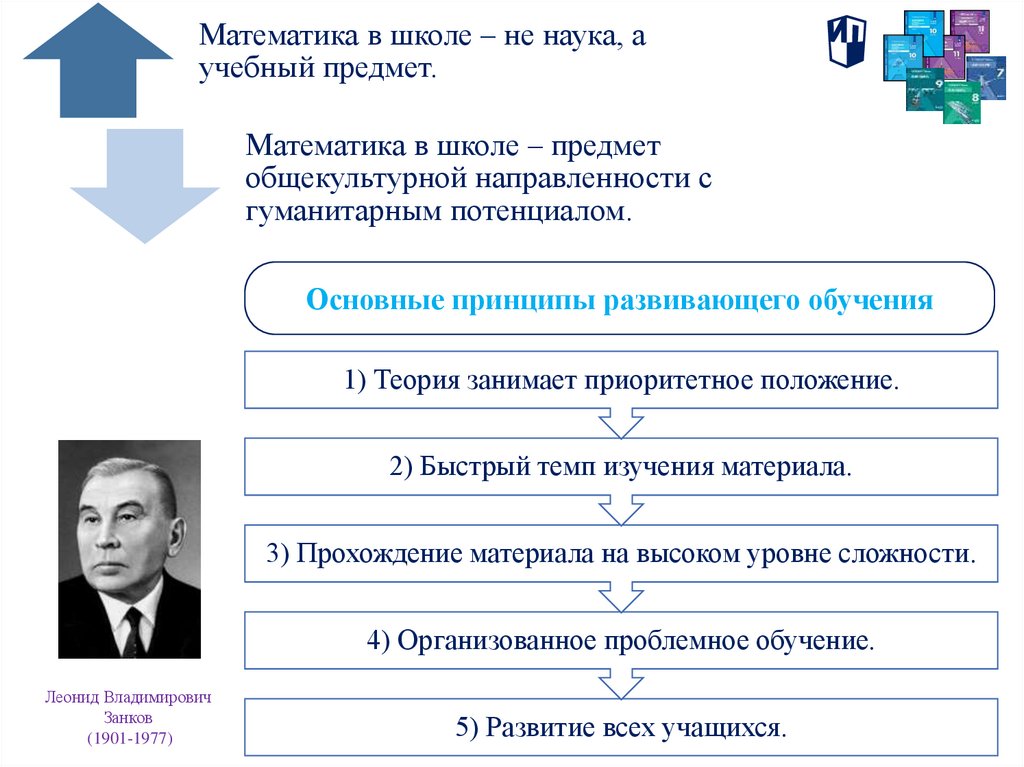
Математика в школе – не наука, аучебный предмет.
Математика в школе – предмет
общекультурной направленности с
гуманитарным потенциалом.
Основные принципы развивающего обучения
1) Теория занимает приоритетное положение.
2) Быстрый темп изучения материала.
3) Прохождение материала на высоком уровне сложности.
4) Организованное проблемное обучение.
Леонид Владимирович
Занков
(1901-1977)
5) Развитие всех учащихся.
6.
Авторы:Мордкович А.Г., Семенов П.В.,
Александрова Л.А., Мардахаева Е.Л.
Алгебра, 7-9 классы
Математика – это язык, на котором
говорят все точные науки.
Н.И.Лобачевский
Класс
Алгебра и начала математического анализа, 10-11 классы
Функция
Реальные и физические процессы
7 класс
Линейная функция. Функция y x 2 .
Равномерные процессы.
8 класс
Квадратичная функция. k
y x, y
Функции
x
Равноускоренные процессы.
9 класс
и
y x.
3
3
Функции y x и y x .
Обобщение изученного в основной школе, формализация некоторых определений и
понятий.
10 класс Тригонометрические функции.
Периодические
процессы,
гармонические колебания.
Степенные, показательные и логарифмические Процессы органического роста.
функции.
11 класс Элементы теории пределов, дифференциального
и интегрального исчисления; обобщение
изученного.
Мгновенная скорость, площадь и
объём, оптимальные значения
некоторых величин.
7.
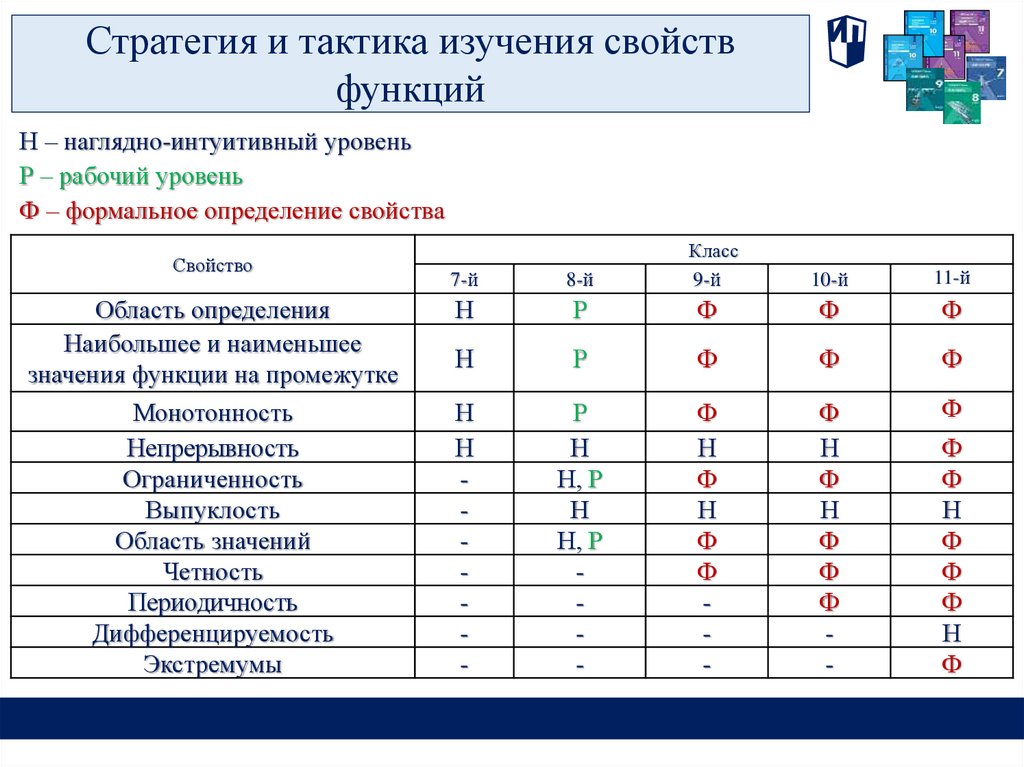
Стратегия и тактика изучения свойствфункций
Н – наглядно-интуитивный уровень
Р – рабочий уровень
Ф – формальное определение свойства
Свойство
Область определения
Наибольшее и наименьшее
значения функции на промежутке
Монотонность
Непрерывность
Ограниченность
Выпуклость
Область значений
Четность
Периодичность
Дифференцируемость
Экстремумы
Класс
9-й
10-й
11-й
Ф
Ф
Ф
Р
Ф
Ф
Ф
Р
Н
Н, Р
Н
Н, Р
-
Ф
Н
Ф
Н
Ф
Ф
-
Ф
Н
Ф
Н
Ф
Ф
Ф
-
Ф
7-й
8-й
Н
Р
Н
Н
Н
-
Ф
Ф
Н
Ф
Ф
Ф
Н
Ф
8.
Содержательное структурирование системыупражнений
преобразование графиков
Инвариантное ядро
в курсе алгебры
состоит из шести
направлений
отыскание наибольшего и наименьшего
значений функции на заданном промежутке
графическое решение уравнений, систем
уравнений и неравенств
функциональная символика
кусочно заданные функции
чтение графика
9.
Ориентация на результат. Повышение IT-компетенций.Упражнения располагаются от простого
к высокому, трёх уровней сложности:
базового,
повышенного,
высокого.
Выделены задания, предназначенные для использования
IT-средств
Ко всем упражнениям, кроме базового
уровня, имеются ответы.
В конце каждого параграфа выделены
упражнения для повторения
10.
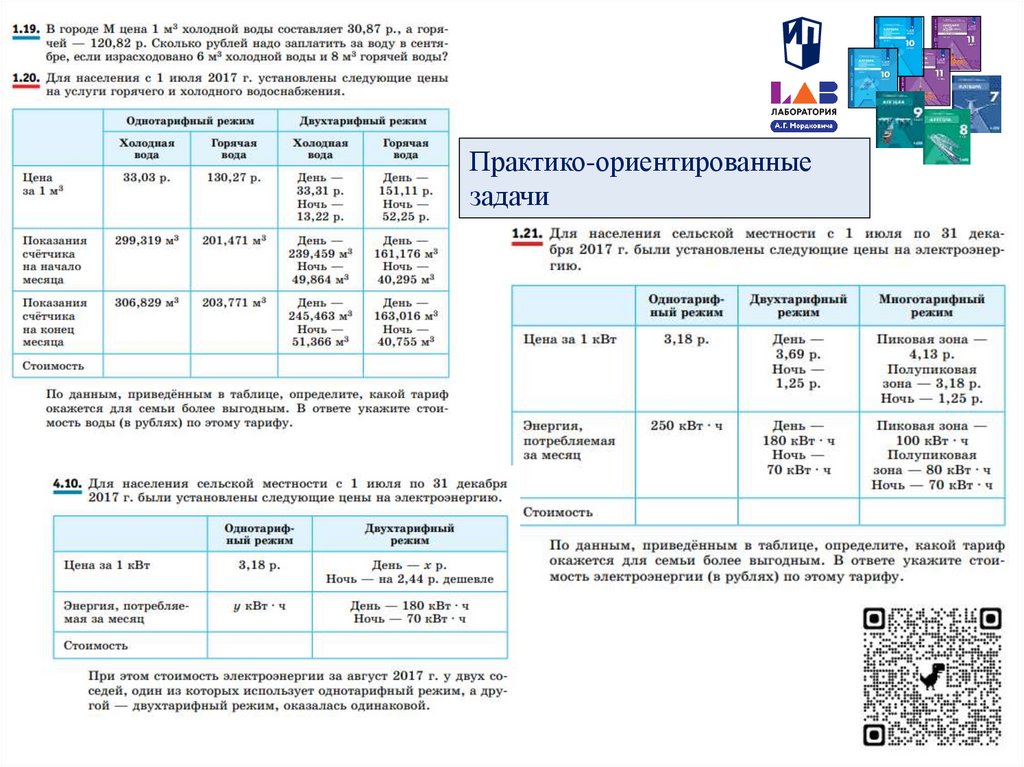
Практико-ориентированныезадачи
11.
Практическое применениематематических знаний
12.
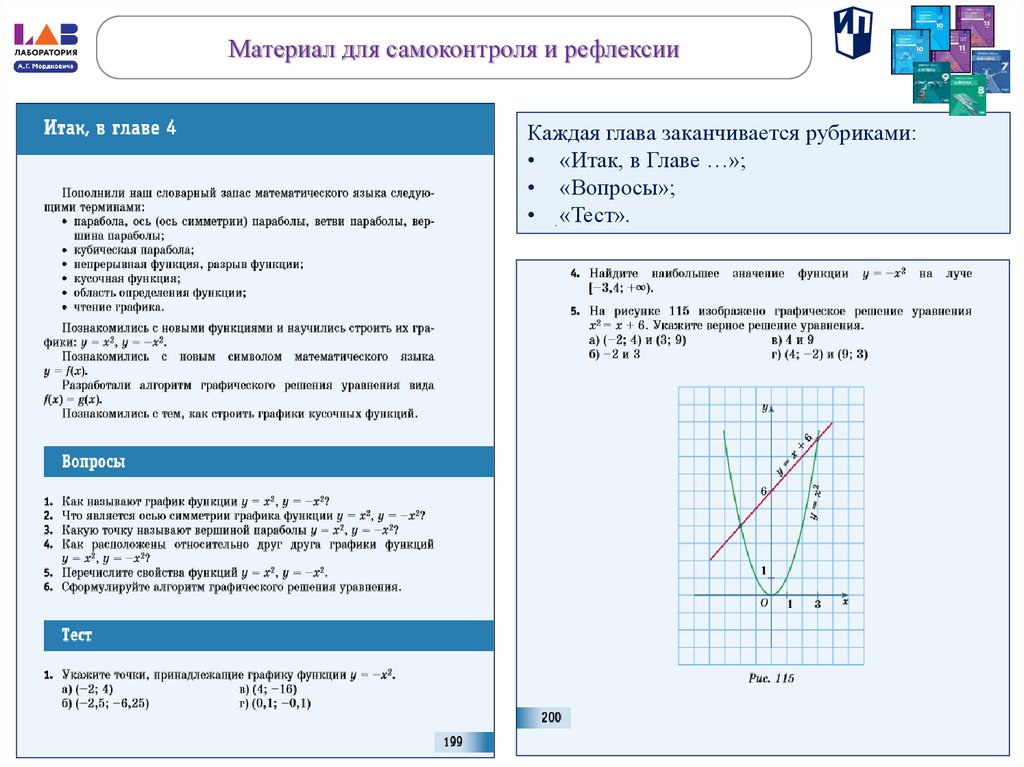
Материал для самоконтроля и рефлексииКаждая глава заканчивается рубриками:
• «Итак, в Главе …»;
• «Вопросы»;
• . «Тест».
13.
Построение индивидуальной образовательной траекторииВ конце каждой главы предложены сведения
из истории математики.
В конце каждой главы есть раздел
«Дополнительные задачи»
14.
Кол-вочасов
Тема
Повторение
Степень
с
натуральным,
действительным показателями.
целым
и
1
Корень степени n > 1 и его свойства.
Иррациональные уравнения.
1
Тождественные преобразования выражений.
Выражения, содержащие корни n–й степени.
Формулы.
1
Преобразование
выражений.
1
тригонометрических
Тригонометрические функции.
1
Тригонометрические уравнения.
1
Логарифм и его свойства. Логарифмические
уравнения.
1
Логарифмические уравнения и неравенства.
1
Показательные уравнения и неравенства.
1
Функции и их свойства. Графики функций.
Касательная.
1
Применение
функций.
1
производной
к
исследованию
Использование вероятностей и статистики при
решении прикладных задач.
1
Примерное планирование
пп
27
28
29
30
31
32
Тема
Кол-во
часов
Глава 6. Уравнения и неравенства.
23
Равносильность уравнений.
Решение уравнений с одной переменной.
Контрольная работа № 6
Решение систем уравнений.
Решение неравенств с одной переменной.
Контрольная работа № 7
Уравнения и неравенства с параметрами.
Уравнения, неравенства и функции в
задачах о среднем арифметическом.
2
4
2
4
4
2
3
2
15.
2. Эффективные приёмы повторения исистематизации теоретического материала.
16.
Составление схемы определения понятияОпределение ближайшего родового понятия.
Выделение видовых отличий.
Структурирование информации.
Арксинус числа а, |a| ≤ 1:
1. Число t
2.
2
t
и
и
2
3. sin t a
arcsin a t
17.
Составление схемы определения понятияОпределение ближайшего родового понятия.
Выделение видовых отличий.
Структурирование информации.
Логарифм числа b по основанию а:
1) b > 0
2) а > 0
3) a ≠ 1
log b
4) a a b
и
и
и
18.
Составление предписания, выражающего общий методрешения задач определённого вида
– выделить тип задач, для которого составляется
предписание – общий метод решения;
– предложить учащимся для решения набор
задач,
включающий
в
себя
задачи,
соответствующие всем пунктам предписания,
которое составляется;
– организовать решение задач учащимися
(оказывая, при необходимости, помощь);
– обобщить решение задач, устанавливая
последовательность действий, которые были
выполнены;
– организовать правильное формулирование
выполненных
действий,
выстроить
последовательность соответствующих блоков
предписания;
– организовать анализ предписания в целом
виде.
Предписание по решению тригонометрических
уравнений вида a cos 2 x b cos x c 0
1. Введём новую переменную cos x z
2
2. Получим уравнение вида az bz c 0
3. Решим квадратное уравнение относительно переменной z
4. Отберём корни, удовлетворяющие условию |z| ≤ 1
5. Вернёмся к прежним переменным cos x z
6. Решим полученное тригонометрическое уравнение x arccos z 2 n, n Z
19.
Составление предписания, выражающего общий методрешения задач определённого вида
Предписание для решения однородного уравнения второй степени
1) убедитесь что cos x ≠ 0;
2) разделите почленно обе части уравнения на cos2 x ≠ 0.
3) воспользуйтесь формулой tg x sin x и преобразуйте уравнение;
cos x
4) введите замену переменной y tg x ;
5) решите полученное квадратное уравнение;
6) сделайте обратную замену, решите полученные тригонометрические уравнения.
20.
Структурирование больших объёмов теоретическогоматериала одного года обучения
Информационная схема
sin x a
cos x a
tgx a
ctgx a
Преобразование
уравнения с помощью
формул
Методы решения
тригонометрических
уравнений
Сведение к
квадратному
Однородные уравнения
Уравнение
sin x a
sin x a
Решение
x 1 arcsin a k , k Z
k
x arcsin a 2 n, x arcsin a 2 n, n Z
Частные случаи
sin x 0
x k, k Z
sin x 1
x
sin x 1
x
2
2 k , k Z
2
2 k , k Z
21.
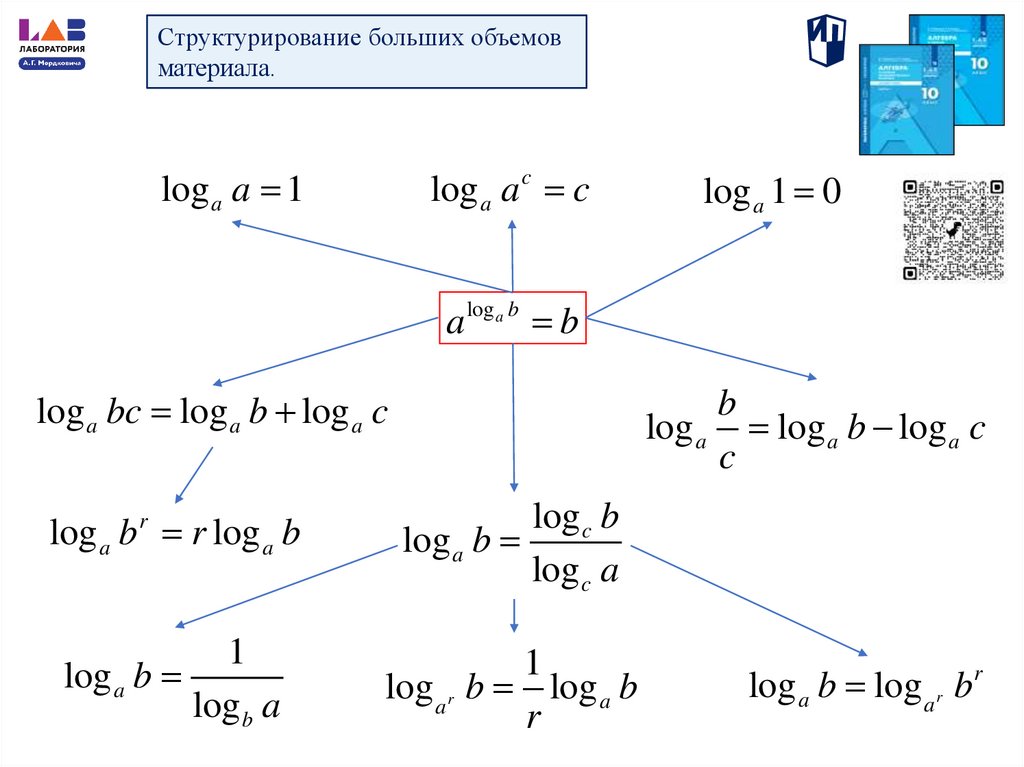
Структурирование больших объемовматериала.
log a a 1
log a a c c
log a 1 0
a loga b b
log a bc log a b log a c
b
log a log a b log a c
c
log a b r r log a b
log c b
log a b
log c a
1
log a b
log b a
1
log ar b log a b
r
log a b log ar b r
22.
3. Примеры применениятеоретических знаний на практике
23.
Уметь решать уравнения и неравенства(базовый уровень)
Задание 1. КИМ DEMO
24.
Умение выполнять вычисления и преобразования(базовый уровень)
Задание 4. КИМ DEMO
25.
Уметь выполнять действия с функциями(повышенный уровень)
Задание 11. КИМ DEMO
26.
Уметь решать уравнения и неравенства(повышенный уровень)
Задание 14. КИМ DEMO
27.
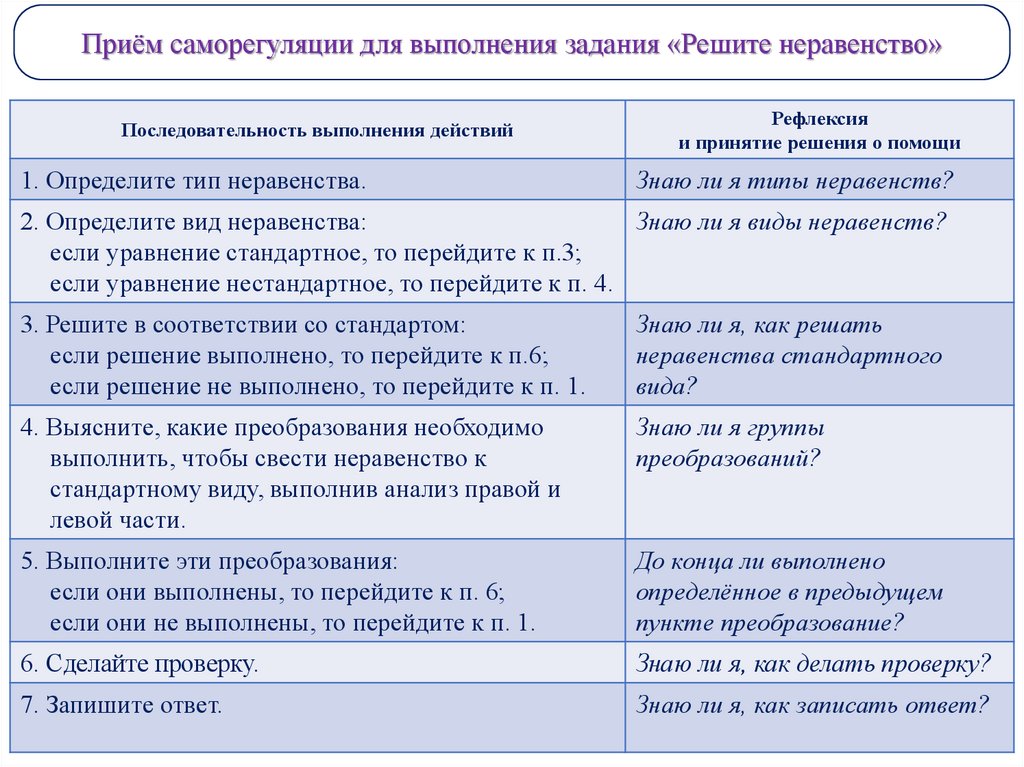
Приём саморегуляции для выполнения задания «Решите неравенство»Последовательность выполнения действий
1. Определите тип неравенства.
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенства:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
Знаю ли я, как решать
неравенства стандартного
вида?
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
6. Сделайте проверку.
Знаю ли я, как делать проверку?
7. Запишите ответ.
Знаю ли я, как записать ответ?
28.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
1. Определите тип неравенства.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенства:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
ОДЗ
x 2 x 20 0,
x 5,
11
x 5
x 4.
0
x 4
Знаю ли я группы
преобразований?
29.
11log11 x 2 x 20 12 log11Решите неравенство
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Последовательность выполнения действий
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
11log11 x 5 x 4 12 log11 x 5 log11 x 4
11
x 5 x 4
11
log11
12
x 5
log11 x 4 12
12
12
ОДЗ
x 5,
x 4.
30.
Решите неравенство11log11 x x 20 12 log11
2
Последовательность выполнения действий
x 5
11
x 4
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
log11 x 4 12
12
log11 x 4 log11 1112
12
x 4 1112
12
x 4 11
ОДЗ
x 5,
x 4.
31.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
1. Определите тип неравенства.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенства:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
x 4 11
11 x 4 11
7 x 15
Ответ: 7; 5 4;15
Знаю ли я, как решать
неравенства стандартного
вида?
ОДЗ
7 x 5, 4 x 15
x 5,
x 4.
32.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
ОДЗ
x 2 x 20 0,
x 5,
11
x 5
x 4.
0
x 4
Знаю ли я группы
преобразований?
33.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
x 5
11
x 4
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
При x 4 :
11log11 x 5 x 4 12 log11 x 5 log11 x 4
11
11log11 x 5 11log11 x 4 11log11 x 5 log11 x 4 12
12 log11 x 4 12
log11 x 4 1
34.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
При x 4 :
x 4 11
x 15
4 x 15
Знаю ли я, как решать
неравенства стандартного
вида?
35.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
x 5
11
x 4
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
При x 5 :
11log11 x 5 x 4 12 log11 x 5 log11 4 x
11
11log11 x 5 11log11 4 x 11log11 x 5 log11 4 x 12
12 log11 4 x 12
log11 4 x 1
36.
Решите неравенство11log11 x 2 x 20 12 log11
Последовательность выполнения действий
1. Определите тип неравенства.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенства:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
При x 5 :
4 x 11
x 7
Ответ: 7; 5 4;15
7 x 5
Знаю ли я, как решать
неравенства стандартного
вида?
37.
Последовательностьвыполнения действий
Рефлексия
и принятие решения о
помощи
Ответ
1. Определите тип уравнения.
Знаю ли я типы
уравнений?
Тригонометрическое
уравнение с одной
переменной.
2. Определите вид уравнения:
если уравнение стандартное, то
перейдите к п.3;
если уравнение нестандартное, то
перейдите к п. 4.
Знаю ли я виды
уравнений?
Уравнение нестандартное.
4. Выясните, какие преобразования
необходимо выполнить, чтобы
свести уравнение к стандартному
виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
Чтобы решить данное
уравнение, необходимо
преобразовать левую часть,
чтобы была одна
тригонометрическая функция.
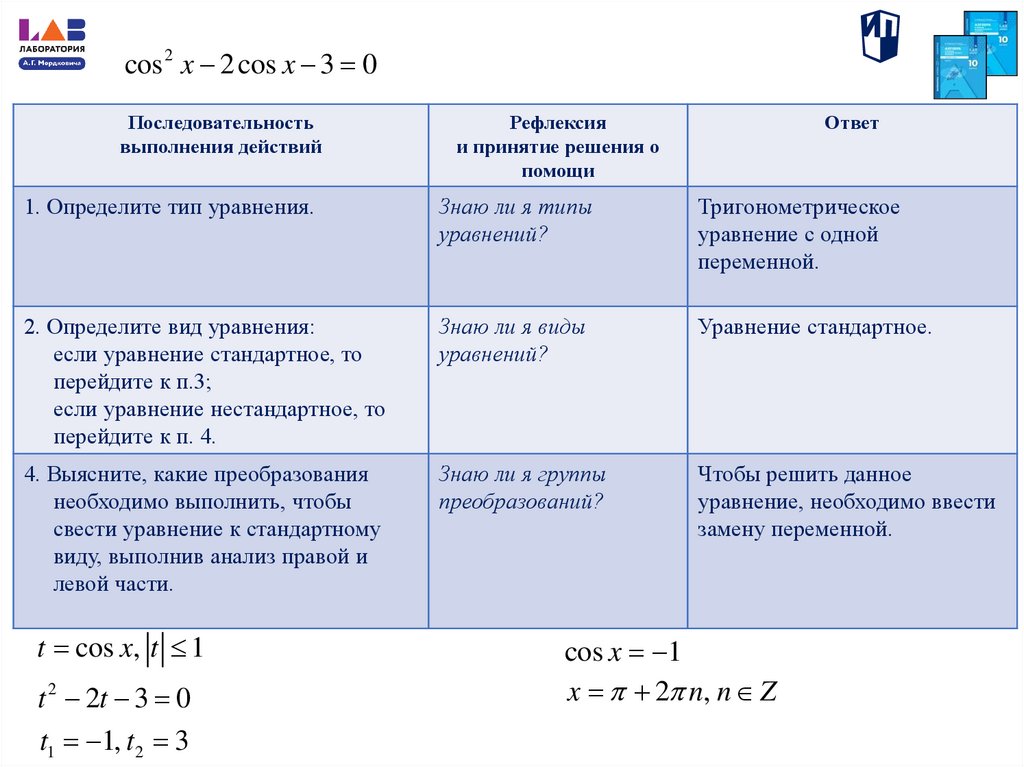
cos 2 x 2 cos x 3 0
38.
cos 2 x 2 cos x 3 0Последовательность
выполнения действий
Рефлексия
и принятие решения о
помощи
Ответ
1. Определите тип уравнения.
Знаю ли я типы
уравнений?
Тригонометрическое
уравнение с одной
переменной.
2. Определите вид уравнения:
если уравнение стандартное, то
перейдите к п.3;
если уравнение нестандартное, то
перейдите к п. 4.
Знаю ли я виды
уравнений?
Уравнение стандартное.
4. Выясните, какие преобразования
необходимо выполнить, чтобы
свести уравнение к стандартному
виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
Чтобы решить данное
уравнение, необходимо ввести
замену переменной.
t cos x, t 1
t 2 2t 3 0
t1 1, t2 3
cos x 1
x 2 n, n Z
39.
Последовательностьвыполнения действий
Рефлексия
и принятие решения о
помощи
Ответ
1. Выясните, выполнено ли требование.
Знаю ли , что такое
требование задачи?
Что следует найти.
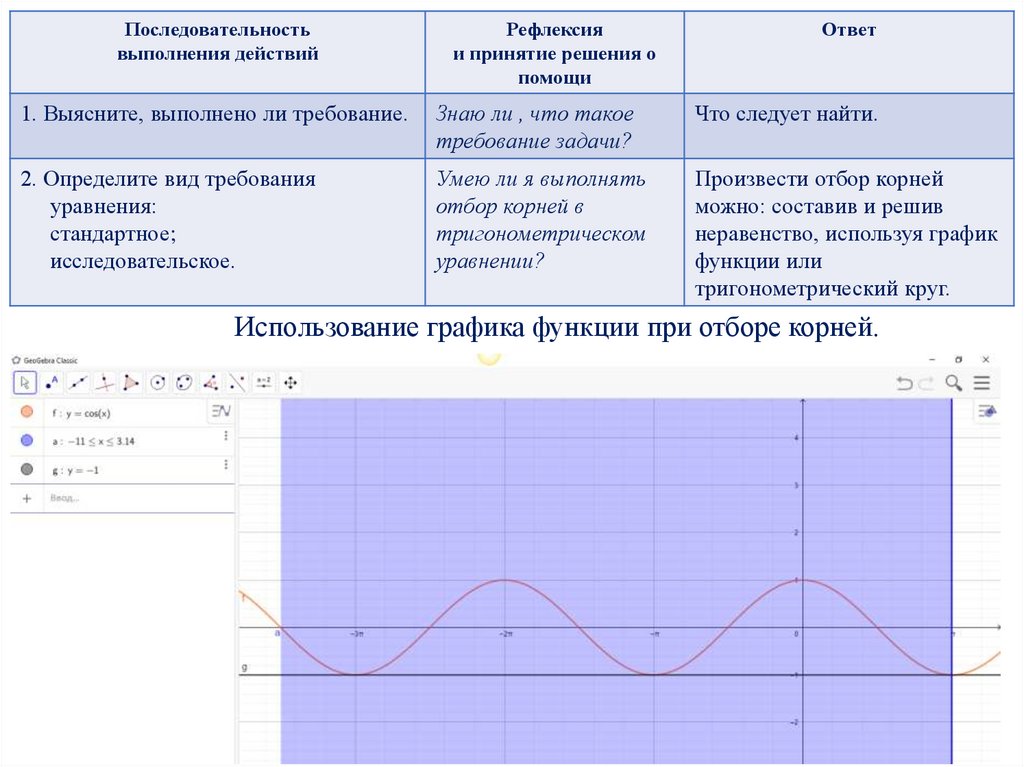
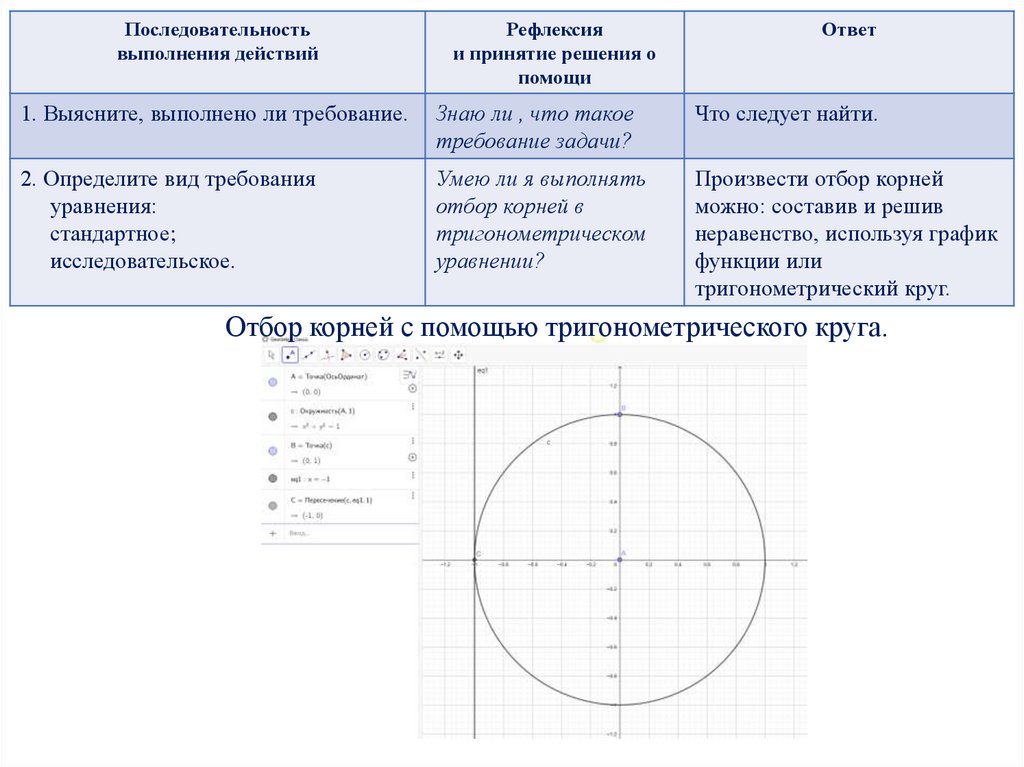
2. Определите вид требования
уравнения:
стандартное;
исследовательское.
Умею ли я выполнять
отбор корней в
тригонометрическом
уравнении?
Произвести отбор корней
можно: составив и решив
неравенство, используя график
функции или
тригонометрический круг.
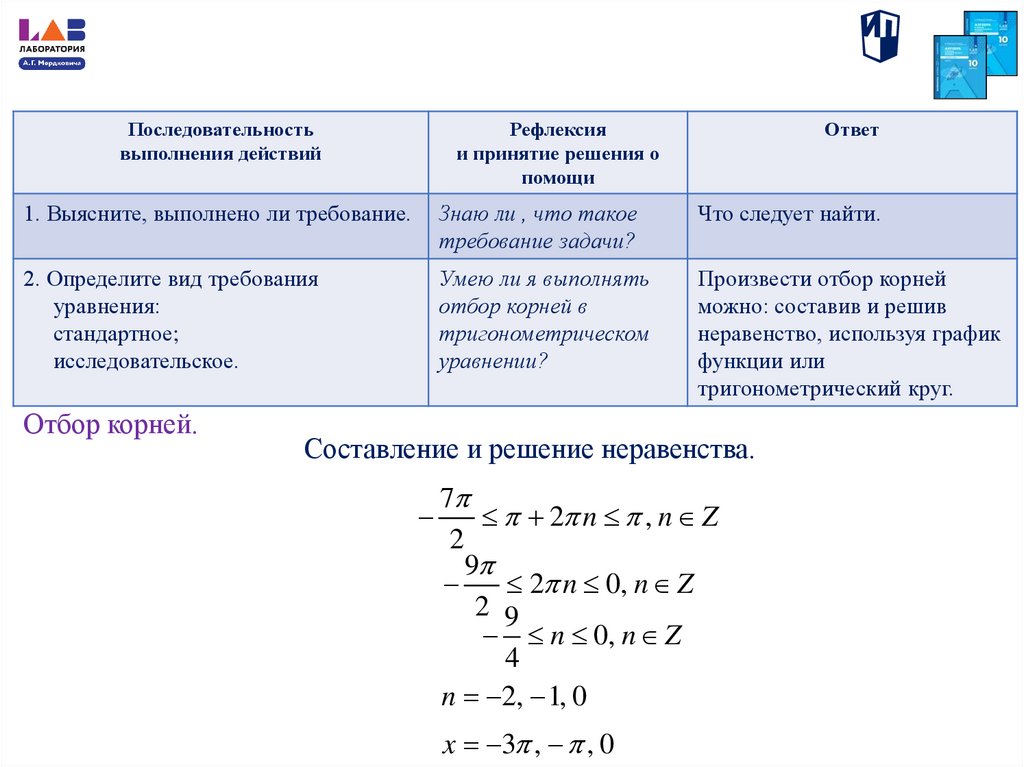
Отбор корней.
Составление и решение неравенства.
7
2 n , n Z
2
9
2 n 0, n Z
2 9
n 0, n Z
4
n 2, 1, 0
x 3 , , 0
40.
Последовательностьвыполнения действий
Рефлексия
и принятие решения о
помощи
Ответ
1. Выясните, выполнено ли требование.
Знаю ли , что такое
требование задачи?
Что следует найти.
2. Определите вид требования
уравнения:
стандартное;
исследовательское.
Умею ли я выполнять
отбор корней в
тригонометрическом
уравнении?
Произвести отбор корней
можно: составив и решив
неравенство, используя график
функции или
тригонометрический круг.
Использование графика функции при отборе корней.
41.
Последовательностьвыполнения действий
Рефлексия
и принятие решения о
помощи
Ответ
1. Выясните, выполнено ли требование.
Знаю ли , что такое
требование задачи?
Что следует найти.
2. Определите вид требования
уравнения:
стандартное;
исследовательское.
Умею ли я выполнять
отбор корней в
тригонометрическом
уравнении?
Произвести отбор корней
можно: составив и решив
неравенство, используя график
функции или
тригонометрический круг.
Отбор корней с помощью тригонометрического круга.
42.
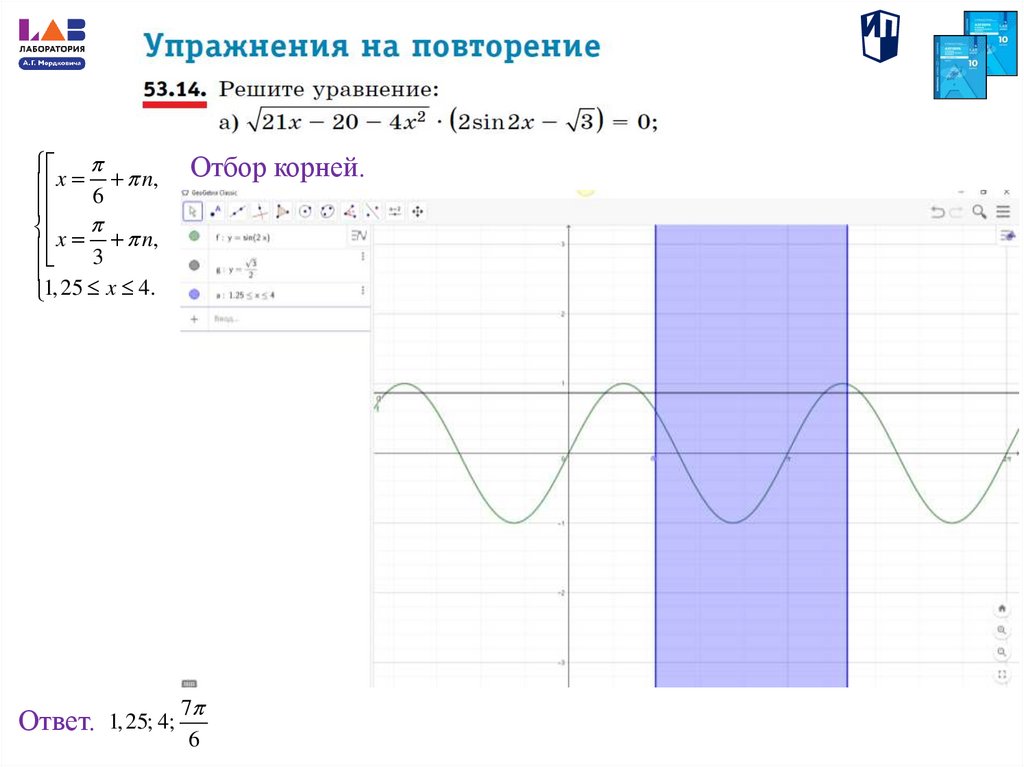
21x 20 4 x 2 0или
x1 1, 25; x2 4
Отбор корней.
1, 25
6
n 4, n Z
15 2
24
n
, n Z
12
6
15 2
24
n
, n Z
12
6
Ответ.
1, 25; 4;
7
6
2sin 2 x 3 0,
2
21x 20 4 x 0.
x
n,
6
x n,
3
1, 25 x 4.
1, 25
3
n 4, n Z
15 3
12
n
, n Z
12
3
15 3
12
n
, n Z
12
3
43.
xn,
6
x n,
3
1, 25 x 4.
Ответ.
1, 25; 4;
Отбор корней.
7
6
44.
УМК «Лаборатория А.Г. Мордковича»Алгебра 7-9 классы. Алгебра и начала математического анализа 10-11 классы
45.
профессор МГПУ, доктор педагогических наук, кандидат физико-математических наук,научный руководитель Международного семинара преподавателей математики педвузов
(1987 г-н.в.);
имеет награды: Премия Президента РФ в области образования, заслуженный деятель науки
РФ, Отличник народного образования, Медаль К.Д.Ушинского.
профессор факультета математики НИУ ВШЭ, доктор физико-математических наук,
профессор, член Федеральной предметной группы по разработке КИМ для ЕГЭ по математике
(2001-2007 гг), разработчик заданий с развернутым ответом, автор более 20 учебнометодических пособий по подготовке учащихся к ЕГЭ и подготовке экспертов к проверке
работ учащихся;
имеет награды: Почётный работник высшего профессионального образования РФ; Почетная
грамота Министерства образования РФ.
учитель математики, методист ГБОУ Школы 1317 г. Москва, учитель высшей категории, член
предметной комиссии по проверке выполнения заданий с развернутым ответом экзаменационных
работ ЕГЭ по математике;
имеет награды: Отличник народного просвещения РФ.
заведующий лабораторией математики ГК «Просвещение», кандидат педагогических наук, доцент,
председатель предметной комиссии ЕГЭ по математике Московской области (2006-2007 гг); членкорреспондент Международной академии научного педагогического образования (МАНПО);
имеет награды: Грант Москвы в сфере образования; Почётная грамота Министерства образования
Московской области.
46.
Отличительные особенностиУМК «Лаборатория А.Г. Мордковича»
Курс построен на основе приоритетности функционально-графической
линии, математическое моделирование является идейным стержнем.
Теория и практика соединены в одну книгу.
Порядок тем соответствует ПООП, отражает психологические
особенности обучающихся.
Выстроена вероятностно-стохастическая линия в тесной взаимосвязи с
основным содержанием.
Каждая глава содержит разделы «Повторение», «Итак, в Главе…»,
«Вопросы», «Дополнительные задачи», «Из истории математики».
Трёхуровневая система заданий отражает требования ФГОС ОО,
итоговой аттестации. Добавлены задачи практического содержания,
высокого уровня сложности.
Включён материал, рекомендованный к изучению с использованием ITсредств.
47.
Алгебра, 7-9 классыАлгебра и начала математического анализа,
10-11 классы
Учебники
Включены в Федеральный перечень
ЭФУ
Примерные рабочие программы
Методические пособия для учителя
Рабочие тетради
Контрольные работы
Самостоятельные и проверочные работы
Алгебраические практикумы
48.
Авторский сайт https://elenamard.jimdo.com49.
Методическая поддержка через сайт издательства http://www.lbz.ru50.
Математика, 5-6 классыАвторы: Н.Б.Истомина,
О.П.Горина, Н.Б.Тихонова
Включены в Федеральный перечень
Учебники
Рабочие тетради
Тестовые задания
Методические пособия для учителя
Пособия для внеурочной деятельности:
«Наглядная геометрия», «Учимся решать
комбинаторные задачи»
51.
Спасибо за внимание!Удачи в делах!
Адрес обратной связи:
kaf.matematika@gmail.com
Авторский сайт:
https://elenamard.jimdo.com/
Сайт издательства:
http://lbz.ru/
Мы готовы с диалогу и будем благодарны, если Вы по
результатам вебинара заполните небольшую анкету по
ссылке или QR:
https://docs.google.com/forms/d/e/1FAIpQLSdfJ1EVQGY
QDG41rgKY8MUAF6GVAPdtn3MSWU_DO79TXNyY0
g/viewform







































 Математика
Математика Образование
Образование








