Похожие презентации:
Профилактика ошибок у выпускников при прохождении итоговой аттестации в условиях дистанционного обучения
1.
Профилактика ошибок увыпускников при прохождении
итоговой аттестации в условиях
дистанционного обучения
2.
DEMO версия КИМ итоговой аттестацииВычисление времени.
Задачи на нахождение процента от числа и числа по его проценту.
Классическое определение вероятности. Полная группа событий.
Равносильный переход в иррациональных и логарифмических
уравнениях.
Вычисления: степени, логарифмы, корни, табличные значения
тригонометрических функций числового аргумента.
Текстовые задачи на смеси, на движение, на совместную работу.
Нахождение наибольшего и наименьшего значений функции с помощью
производной и без.
3.
Поиск ошибки в готовом решенииЗадание 1:
Показания счётчика электроэнергии 1 января составляли 28 897 кВт/ч, а 1 февраля –
29 212 кВт/ч. Стоимость 1 кВт/ч электроэнергии составляет 3 р. 45 коп. При оплате через
взимается комиссия в размере 3%. Какую сумму необходимо оплатить за электроэнергию
в январе? Ответ дайте в рублях и копейках.
Решение 1:
29212 28897 315 кВт/ч
315 3, 45 1086, 75 р.
1086, 75 1087 р.
1087 1, 03 1119, 61 р.
Ответ: 1119 р. 61 коп.
4.
Поиск ошибки в готовом решенииЗадание 1:
Показания счётчика электроэнергии 1 января составляли 28 897 кВт/ч, а 1 февраля –
29 212 кВт/ч. Стоимость 1 кВт/ч электроэнергии составляет 3 р. 45 коп. При оплате через
взимается комиссия в размере 3%. Какую сумму необходимо оплатить за электроэнергию
в январе? Ответ дайте в рублях и копейках.
Решение 2:
29212 28897 315 кВт/ч
315 3, 45 1086, 75 р.
1086, 75 1, 03 1119,3525 р.
1119,3525... 1119 р. 35 коп.
Ответ: 1119 р. 35 коп.
5.
Поиск ошибки в готовом решенииЗадание 1:
Показания счётчика электроэнергии 1 января составляли 28 897 кВт/ч, а 1 февраля –
29 212 кВт/ч. Стоимость 1 кВт/ч электроэнергии составляет 3 р. 45 коп. При оплате через
взимается комиссия в размере 3%. Какую сумму необходимо оплатить за электроэнергию
в январе? Ответ дайте в рублях и копейках.
Решение 3:
29212 28897 315 кВт/ч
315 3, 45 1086, 75 р.
1086, 75 1087 р.
1087 : 0,97 1120, 6185567...
1120, 6185567... 1120 р. 62 коп.
Ответ: 1120 р. 62 коп.
6.
Поиск ошибки в готовом решенииЗадание 1:
Показания счётчика электроэнергии 1 января составляли 28 897 кВт/ч, а 1 февраля –
29 212 кВт/ч. Стоимость 1 кВт/ч электроэнергии составляет 3 р. 45 коп. При оплате через
взимается комиссия в размере 3%. Какую сумму необходимо оплатить за электроэнергию
в январе? Ответ дайте в рублях и копейках.
Решение 4:
29212 28897 315 кВт/ч
315 3, 45 1086, 75 р.
1086, 75 : 0,97 1120,36082474...
1120,36082474... 1120 р. 36 коп.
Ответ: 1120 р. 36 коп.
7.
Поиск ошибки в готовом решенииЗадание 4:
В сундуке лежат 4 золотые монеты и 2 серебряные. Пират наугад вытаскивает 2 монеты.
Какова вероятность того, что они обе серебряные?
Решение 1:
При вынимании двух монет возможны три исхода:
две золотые,
две серебряные,
золотая и серебряная монеты.
Благоприятствующий описанному в задаче событию 1 исход.
1
Ответ:
3
8.
Поиск ошибки в готовом решенииЗадание 4:
В сундуке лежат 4 золотые монеты и 2 серебряные. Пират наугад вытаскивает 2 монеты.
Какова вероятность того, что они обе серебряные?
Решение 2:
Всего равновозможных несовместных исходов:
6 5
15
2
Благоприятный описанному в задаче событию 1 исход.
1
Ответ:
4
9.
Поиск ошибки в готовом решенииЗадание 4:
Монету бросили три раза. Какова вероятность, что выпадет один орёл?
Решение 1:
При бросании трёх монет возможны четыре исхода:
3 орла;
2 орла и 1 решка;
2 решки и 1 орёл;
3 решки.
Благоприятствующий описанному в задаче событию 1 исход.
1
Ответ:
4
10.
Поиск ошибки в готовом решенииЗадание 4:
Монету бросили три раза. Какова вероятность, что выпадет один орёл?
Решение 2:
При бросании трех монет возможны исходы:
1 монета
2 монета
3 монета
Орёл
Решка
Орёл
Орёл
Орёл
Решка
Решка
Решка
Орёл
Орёл
Решка
Орёл
Решка
Решка
Орёл
Решка
Орёл
Орёл
Орёл
Решка
Решка
Орёл
Решка
Решка
Благоприятствующих описанному в задаче событию 3 исхода.
3
Ответ:
8
11.
Поиск ошибки в готовом решенииЗадание 5:
18 21x 2 x.
Найдите корень уравнения
Если уравнение имеет более одного корня, укажите меньший из
них.
Решение 1:
18 21x
2
2x
2
4 x 2 21x 18 0
x1 6, x2 0, 75
Ответ:
6.
12.
Поиск ошибки в готовом решенииЗадание 5:
Найдите корень уравнения
18 21x 2 x.
Если уравнение имеет более одного корня, укажите меньший из
них.
Решение 2:
18 21x 2 2 x 2 ,
18 21x 2 x
18 21x 0
x 6,
4 x 2 21x 18 0,
x 6,
x 0, 75,
6
6
x 0, 75.
x
7
x 7
Ответ:
6.
13.
Поиск ошибки в готовом решенииЗадание 5:
Найдите корень уравнения
18 21x 2 x.
Если уравнение имеет более одного корня, укажите меньший из
них.
Решение 3:
18 21x
18 21x 2 x
2 x 0
2
2x ,
2
x 6,
4 x 2 21x 18 0,
x 0, 75, x 0, 75.
x 0
x 0
Ответ: 0, 75.
14.
Поиск ошибки в готовом решенииЗадание 5:
18 21x 2 x.
Найдите корень уравнения
Если уравнение имеет более одного корня, укажите меньший из
них.
Решение 4:
18 21x
2
2x
2
4 x 2 21x 18 0
x1 6, x2 0, 75
x1 6
Проверка:
18 21 6 2 6
Неверное равенство
Ответ: 0, 75.
x2 0, 75
18 21 0, 75 1,5
Верное равенство
15.
Поиск ошибки в готовом решенииЗадание 19:
На доске написано более 42, но менее 54 целых чисел. Среднее арифметическое этих
чисел равно −7, среднее арифметическое всех положительных из них равно 6, а среднее
арифметическое всех отрицательных из них равно −12.
а) Сколько чисел написано на доске?
б) Каких чисел больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение 1:
х – количество положительных чисел;
у – количество отрицательных чисел
х + у – количество всех чисел
а) Сколько чисел написано на доске?
−7(х + у) = 6х – 12у
−7(х + у) = 6(х – 2у)
42 < х + у < 54
х + у = 48
б) Каких чисел больше: положительных или отрицательных?
−7(х + у) = 6х – 12у,
х + у = 48
13х – 5у = 0,
у = 48 – х
18х = 240
х = 13
1
3
в) Какое наибольшее количество положительных чисел может быть среди них?
16.
Поиск ошибки в готовом решенииЗадание 19:
На доске написано более 42, но менее 54 целых чисел. Среднее арифметическое этих
чисел равно −7, среднее арифметическое всех положительных из них равно 6, а среднее
арифметическое всех отрицательных из них равно −12.
а) Сколько чисел написано на доске?
б) Каких чисел больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение 2:
а) Сколько чисел написано на доске?
х – количество положительных чисел;
−7(х + у +z) = 6х – 12у
у – количество отрицательных чисел;
−7(х + у + z) = 6(х – 2у)
z – количество нулей
42 < х + у + z < 54
х + у + z– количество всех чисел
х + у + z = 48
Вывод: всего записано 48 чисел.
б) Каких чисел больше: положительных или отрицательных?
−7(х + у + z) = 6(х – 2у),
х + у + z = 48
–х + 2у = 56,
x+ у + z = 48
x – y = 12 – 2k – (34 – k) = –22 – k < 0
Вывод: отрицательных чисел больше.
3у + z = 104
z = 3k + 2
у = 34 – k
x = 12 – 2k
17.
Поиск ошибки в готовом решенииЗадание 19:
На доске написано более 42, но менее 54 целых чисел. Среднее арифметическое этих
чисел равно −7, среднее арифметическое всех положительных из них равно 6, а среднее
арифметическое всех отрицательных из них равно −12.
а) Сколько чисел написано на доске?
б) Каких чисел больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение 2:
х – количество положительных чисел;
у – количество отрицательных чисел;
z – количество нулей
х + у + z– количество всех чисел
в) Какое наибольшее количество положительных чисел может быть среди них?
x = 12 – 2k
x≤0
Например,
12 положительных чисел равных 6
34 отрицательных числа равных – 12
2 нуля
Вывод: 12 – наибольшее количество положительных чисел.
18.
Применение нескольких способов решенияЗадание 13:
а) Решите уравнение
3cos x
9cos
2
x
42cos
2
x cos x
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
3cos x
9cos
1
3
2
x
42cos
2
x cos x
2cos 2 x cos x
42cos
1
12
2
x cos x
2cos 2 x cos x
1
2 cos 2 x cos x 0
cos x 2 cos x 1 0
cos x 0
x
2
n, n Z
или
2 cos x 1 0
x
3
2 k , k Z
7 11
2 ; 6
19.
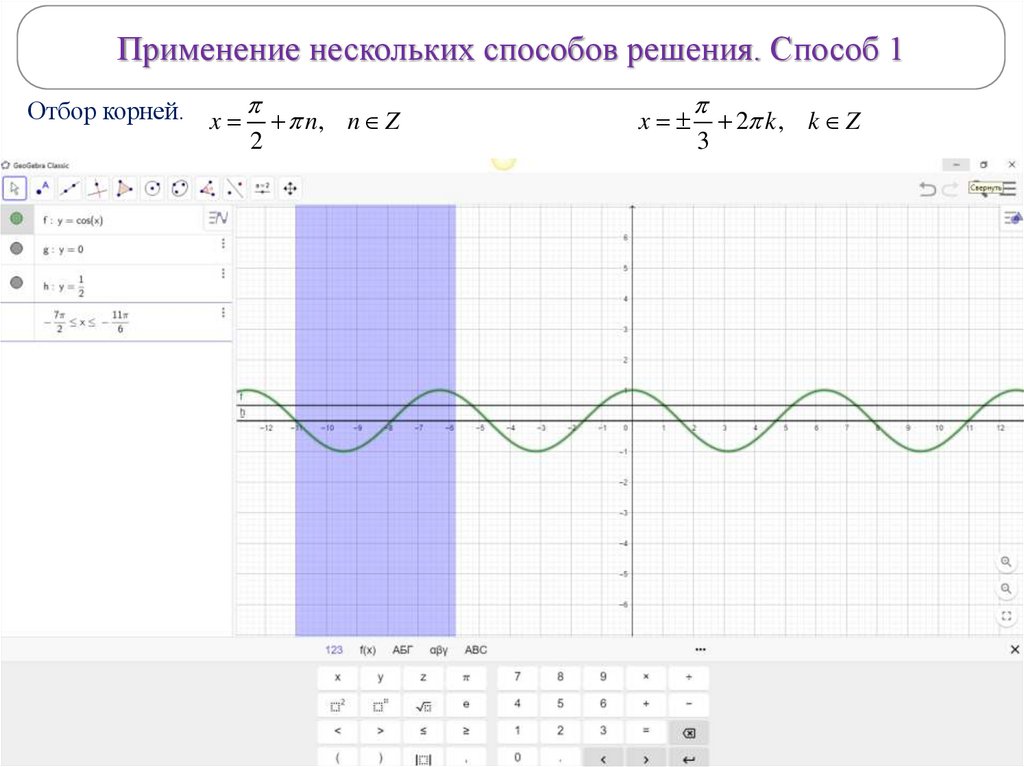
Применение нескольких способов решения. Способ 1Отбор корней. x n, n Z
2
x
3
2 k , k Z
20.
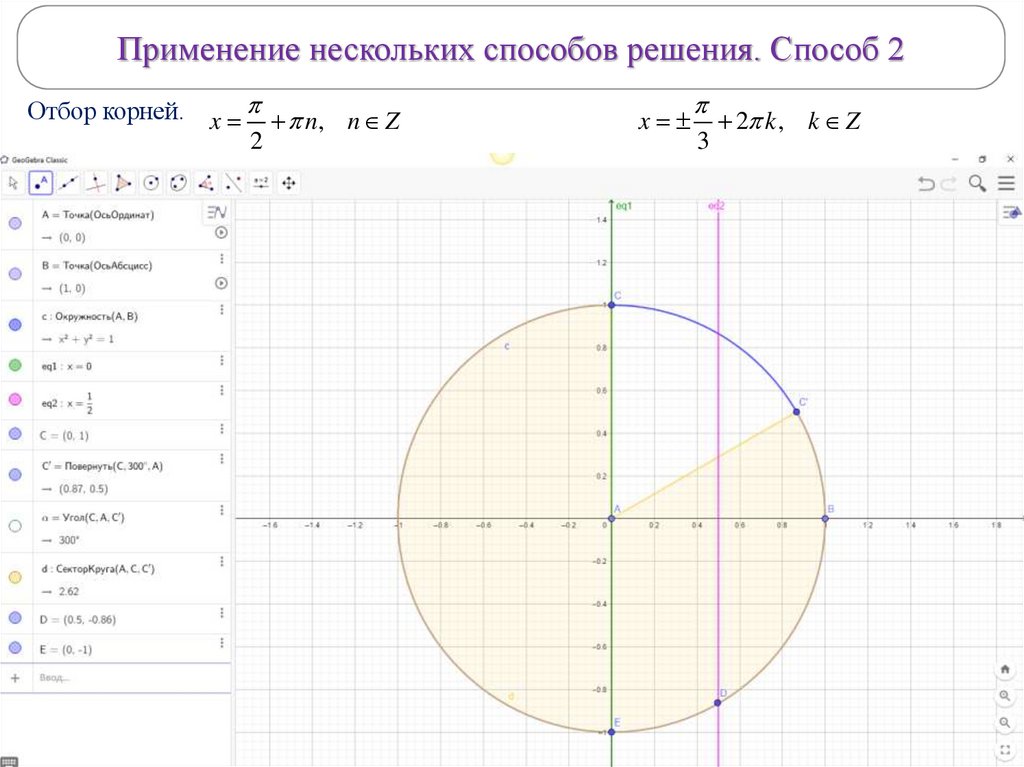
Применение нескольких способов решения. Способ 2Отбор корней. x n, n Z
2
x
3
2 k , k Z
21.
Применение нескольких способов решения. Способ 3Отбор корней.
7
11
n
, n Z
2
2
6
4 n
7
, n Z
3
7
4 n , n Z
3
n 4; 3
x
Ответ: а)
7
5
,
2
2
2
n, n Z ;
б) 7 ,
2
7
11
2 k
, k Z
2
3
6
19
3
2 k , k Z
6
2
19
3
k , k Z
12
4
7
k 1
x
3
3
2 k , k Z .
5
7
,
.
2
3
7
11
2 k
, k Z
2
3
6
23
13
2 k
, k Z
6
6
23
13
k , k Z
12
12
22.
Типовые задания, направленные на формированиесамоконтроля
Типовое задание 1. Составление схемы определения понятия.
Анализ, сравнение, обобщение, структурирование информации.
Типовое задание 4. Составление предписания, выражающего общий метод решения
задач определённого типа.
Анализ, синтез, сравнение, структурирование информации, достраивание,
алгоритмизация.
Типовое задание 5. Составление информационной схемы
Анализ, синтез, сравнение, обобщение, структурирование, достраивание
информации.
Типовое задание 6. Составление схемы поиска решения задачи.
Анализ, синтез, выведение следствий, достраивание информации, моделирование.
Боженкова Л.И. Методика формирования универсальных учебных действий при
обучении алгебре. – М.: Лаборатория знаний, 2016. – 240 с.
23.
Схема определения понятияАрксинус числа а:
1) Число t
2) t ;
2 2
3) sin t a
Примеры:
arcsin
и
и
3
3
sin
2
3
3
2
24.
Схема определения понятияесли 1 a 1, то
sin t a,
arcsin a t
t .
2
2
Примеры:
arcsin
3
3
sin
2
3
3
2
25.
Схема определения понятияКорень квадратный из неотрицательного числа а:
и
1) Неотрицательное число
2) Квадрат этого числа равен а.
Показатель корня
(2 не пишется)
a 0,
Квадратный корень из
неотрицательного числа а
2
Подкоренное
выражение
a
a
2
a, a 0
26.
Схема определения понятияЛогарифм положительного числа b по основанию а:
1) Показатель степени
2) Основание а положительное
3) Основание а отлично от 1
4) а в этой степени равно b
a loga b b
и
и
и
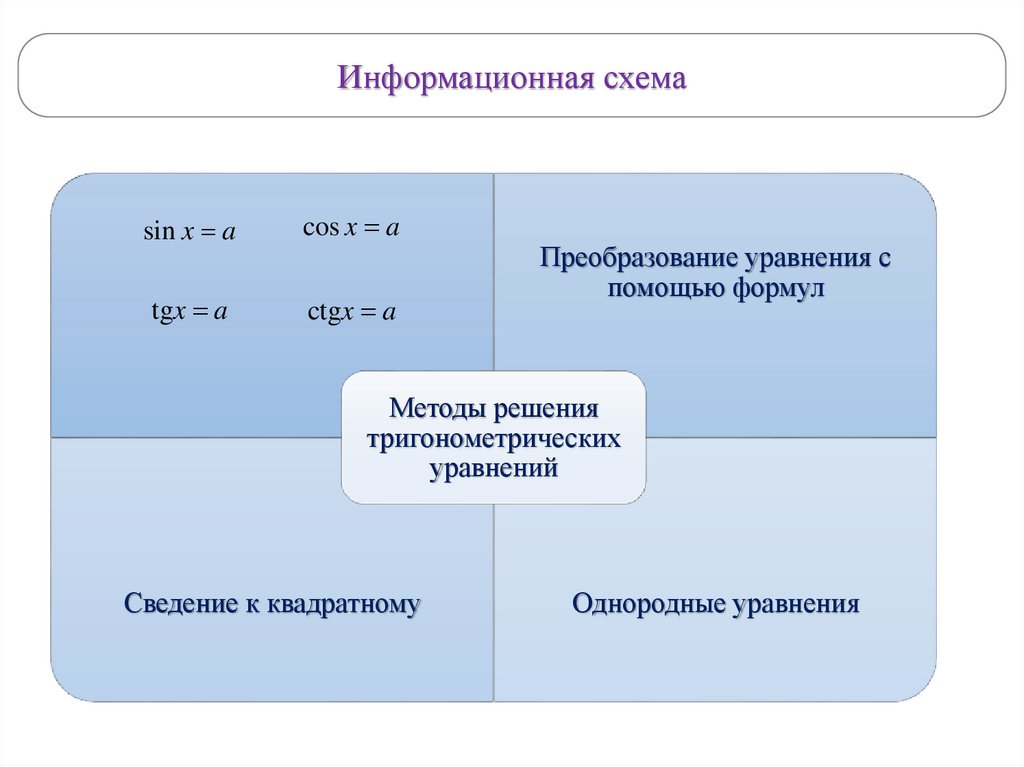
27.
Информационная схемаsin x a
cos x a
tgx a
ctgx a
Преобразование уравнения с
помощью формул
Методы решения
тригонометрических
уравнений
Сведение к квадратному
Однородные уравнения
28.
Составление предписания, выражающего общийметод решения задач
Предписание для решения тригонометрического уравнения
сведением к квадратному
1. Ввести новую переменную sin x z ;
2. выполнить подстановку и получить квадратное
уравнение;
3. решить квадратное уравнение;
4. сделать обратную замену;
5. решить полученные простейшие тригонометрические
уравнения.
29.
Приём саморегуляции для выполнения задания «Решите уравнение»Последовательность выполнения действий
1. Определите тип уравнения.
Рефлексия
и принятие решения о помощи
Знаю ли я типы уравнений?
2. Определите вид уравнения:
Знаю ли я виды уравнений?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
Знаю ли я, как решать уравнения
стандартного вида?
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести уравнение к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
6. Сделайте проверку.
Знаю ли я, как делать проверку?
7. Запишите ответ.
Знаю ли я, как записать ответ?
30.
Приём саморегуляции для выполнения задания «Решите неравенство»Последовательность выполнения действий
1. Определите тип неравенство.
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
Знаю ли я, как решать
неравенства стандартного
вида?
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
6. Сделайте проверку.
Знаю ли я, как делать проверку?
7. Запишите ответ.
Знаю ли я, как записать ответ?
31.
Приём саморегуляции для выполнения задания «Решите неравенство»Последовательность выполнения действий
1. Определите тип неравенство.
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
Знаю ли я, как решать
неравенства стандартного
вида?
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
6. Сделайте проверку.
Знаю ли я, как делать проверку?
7. Запишите ответ.
Знаю ли я, как записать ответ?
32.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
Решение 1:
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
ОДЗ
x 2 x 20 0,
x 5,
11
x 5
x 4.
0
x 4
Знаю ли я группы
преобразований?
33.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
11log11 x 2 x 20 12 log11
Решите неравенство
x 5
Решение 1:
11
x 4
Рефлексия
и принятие решения о помощи
Последовательность выполнения действий
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
11log11 x 5 x 4 12 log11 x 5 log11 x 4
11
x 5 x 4
11
log11
12
x 5
log11 x 4 12
12
12
ОДЗ
x 5,
x 4.
34.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решение 1:
Последовательность выполнения действий
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
log11 x 4 12
12
log11 x 4 log11 1112
12
x 4 1112
12
x 4 11
ОДЗ
x 5,
x 4.
35.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решение 1:
Последовательность выполнения действий
1. Определите тип неравенство.
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
x 4 11
11 x 4 11
7 x 15
Ответ: 7; 5 4;15
Знаю ли я, как решать
неравенства стандартного
вида?
ОДЗ
7 x 5, 4 x 15
x 5,
x 4.
36.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
Решение 2:
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
ОДЗ
x 2 x 20 0,
x 5,
11
x 5
x 4.
0
x 4
Знаю ли я группы
преобразований?
37.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
x 5
Решение 2:
Последовательность выполнения действий
11
x 4
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
При x 4 :
11log11 x 5 x 4 12 log11 x 5 log11 x 4
11
11log11 x 5 11log11 x 4 11log11 x 5 log11 x 4 12
12 log11 x 4 12
log11 x 4 1
38.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
Решение 2:
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
При x 4 :
x 4 11
x 15
4 x 15
Знаю ли я, как решать
неравенства стандартного
вида?
39.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
x 5
Решение 2:
Последовательность выполнения действий
11
x 4
Рефлексия
и принятие решения о помощи
4. Выясните, какие преобразования необходимо
выполнить, чтобы свести неравенство к
стандартному виду, выполнив анализ правой и
левой части.
Знаю ли я группы
преобразований?
5. Выполните эти преобразования:
если они выполнены, то перейдите к п. 6;
если они не выполнены, то перейдите к п. 1.
До конца ли выполнено
определённое в предыдущем
пункте преобразование?
При x 5 :
11log11 x 5 x 4 12 log11 x 5 log11 4 x
11
11log11 x 5 11log11 4 x 11log11 x 5 log11 4 x 12
12 log11 4 x 12
log11 4 x 1
40.
Приём саморегуляции для выполнения задания «Решите неравенство»Задание 15:
Решите неравенство
11log11 x 2 x 20 12 log11
Решение 2:
Последовательность выполнения действий
1. Определите тип неравенство.
x 5
11
x 4
Рефлексия
и принятие решения о помощи
Знаю ли я типы неравенств?
2. Определите вид неравенство:
Знаю ли я виды неравенств?
если уравнение стандартное, то перейдите к п.3;
если уравнение нестандартное, то перейдите к п. 4.
3. Решите в соответствии со стандартом:
если решение выполнено, то перейдите к п.6;
если решение не выполнено, то перейдите к п. 1.
При x 5 :
4 x 11
x 7
Ответ: 7; 5 4;15
7 x 5
Знаю ли я, как решать
неравенства стандартного
вида?
41.
Электронный ресурс «МАТЕМАТИКА. Открытый урок сБИНОМ»
https://edu.lbz.ru
42.
Электронный ресурс «МАТЕМАТИКА. Открытый урок сБИНОМ»
https://edu.lbz.ru
43.
Электронный ресурс «МАТЕМАТИКА. Открытый урок сБИНОМ»
https://edu.lbz.ru
44.
Электронный ресурс «МАТЕМАТИКА. Открытый урок сБИНОМ»
https://edu.lbz.ru
45.
Электронный ресурс «Онлайн-уроки»Официальный сайт: https://prosv.ru
46.
Телевизионный проект «Моя школа online»Официальный сайт: https://otr-online.ru
47.
профессорМосковского
городского
педагогического
университета; доктор педагогических наук, кандидат физикоматематических наук, профессор; заслуженный деятель науки
РФ, лауреат премии Президента РФ в области образования
(2001); научный руководитель Международного семинара
преподавателей математики педвузов.
Автор более 100 книг, среди которых учебники
для школы по алгебре, учебные пособия для
педвузов по элементарной математике и по
математическому
анализу,
различные
справочные пособия, пособия для поступающих
в вузы, книги для учителей, факультативные
курсы
48.
профессор факультета математики НИУ ВШЭ; доктор физикоматематических наук, профессор; член Федеральной предметной группы поразработке КИМ для ЕГЭ по математике, разработчик заданий с
развернутым ответом (2001-2007 гг.); соавтор более 20 учебно-методических
пособий по подготовке учащихся к ЕГЭ и подготовке экспертов к проверке
работ учащихся;
имеет награды: Почётный работник ВПО РФ; Почетная грамота
Министерства образования РФ; лучший преподаватель (2018, 2019).
учитель математики, методист ГБОУ Школы 1317 г. Москва, учитель высшей
категории, член предметной комиссии по проверке выполнения заданий с
развернутым ответом экзаменационных работ ЕГЭ по математике;
имеет награды: Отличник народного просвещения РФ.
заведующая лабораторией математики издательства «БИНОМ. Лаборатория
знаний», кандидат педагогических наук, доцент, председатель предметной
комиссии ЕГЭ по математике Московской области 2006-2007 гг; членкорреспондент Международной академии научного педагогического образования
(МАНПО);
имеет награды: Грант Москвы в сфере образования (2010), Почётная грамота
Министерства образования Московской области.
49.
Приказот 22 ноября 2019 г.
№ 632
В
соответствии
с
Приказом
Минпросвещения России № 632 от 22
ноября 2019 г. «О внесении
изменений в Федеральный перечень
учебников,
рекомендуемых
к
использованию
при
реализации
имеющих
государственную
аккредитацию
образовательных
программ
начального
общего,
основного общего, среднего общего
образования,
сформированный
приказом Министерства просвещения
Российской Федерации от 28 декабря
2018 г. № 345» в федеральный
перечень
учебников
вошли
следующие
учебники
издательства «БИНОМ. Лаборатория
знаний»
50.
Мордкович А.Г., Семенов П.В., Александрова Л.А.,Мардахаева Е.Л. Алгебра. 7 класс. – М. : БИНОМ.
Лаборатория знаний.
Мордкович А.Г., Семенов П.В., Александрова Л.А.,
Мардахаева Е.Л. Алгебра. 8 класс. – М. : БИНОМ.
Лаборатория знаний.
Мордкович А.Г., Семенов П.В., Александрова Л.А.,
Мардахаева Е.Л. Алгебра. 9 класс. – М. : БИНОМ.
Лаборатория знаний.
51.
Состав УМК по алгебреУчебник
ЭФУ
Сборник программ
Методическое пособие для учителя
Рабочие тетради
Контрольные работы
Практикум
Тематический контроль
Самостоятельные и проверочные работы
Комплект для 7 класса
52.
Находятся на экспертном совете на 2020 годс положительными заключениями
Мордкович А.Г., Семенов П.В., Александрова Л.А.,
Мардахаева Е.Л. Математика: алгебра и начала
математического анализа, геометрия. Алгебра и
начала математического анализа: базовый уровень:
10 класс В 2 ч. – М. : БИНОМ. Лаборатория знаний.
Мордкович А.Г., Семенов П.В., Александрова Л.А.,
Мардахаева Е.Л. Математика: алгебра и начала
математического анализа, геометрия. Алгебра и
начала математического анализа: базовый уровень:
11 класс В 2 ч. – М. : БИНОМ. Лаборатория знаний.
53.
Авторский сайтhttps://elenamard.jimdo.com
54.
Спасибо за внимание!Удачи в делах!
Адрес обратной связи:
kaf.matematika@gmail.com
Авторский сайт:
https://elenamard.jimdo.com
Сайт издательства:
http://lbz.ru
Мы готовы с диалогу!



















































 Образование
Образование








