Функции. Функция арифметического квадратного корня

1. Китайская пословица гласит: « Я слушаю,-я забываю; Я вижу,-я запоминаю; Я делаю,- я усваиваю»

2.

Функция арифметического
квадратного корня
у х

3. «Из истории математики» Впервые слово «функция» употребил Готфрид Вильгельм Лейбниц еще в XVII веке (слово «функция» происходит

от латинского functio — исполнение,
осуществление)
В 1637 году Декарт дает первое
определение функции
В 1755 году
Леонард Эйлер
дает общее
определение
функции
В 1671 году Ньютон
под функцией стал
понимать
переменную
величину, которая
изменяется с
течением времени.

4. Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное

Определение функции
Функция – это зависимость переменной у
от переменной х, при которой каждому
значению переменной х соответствует
единственное значение переменной у.
х–независимая переменная или аргумент
у–зависимая переменная или значение
функции

5. Что называют графиком функции? Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а

ординаты –
соответствующим значениям функции

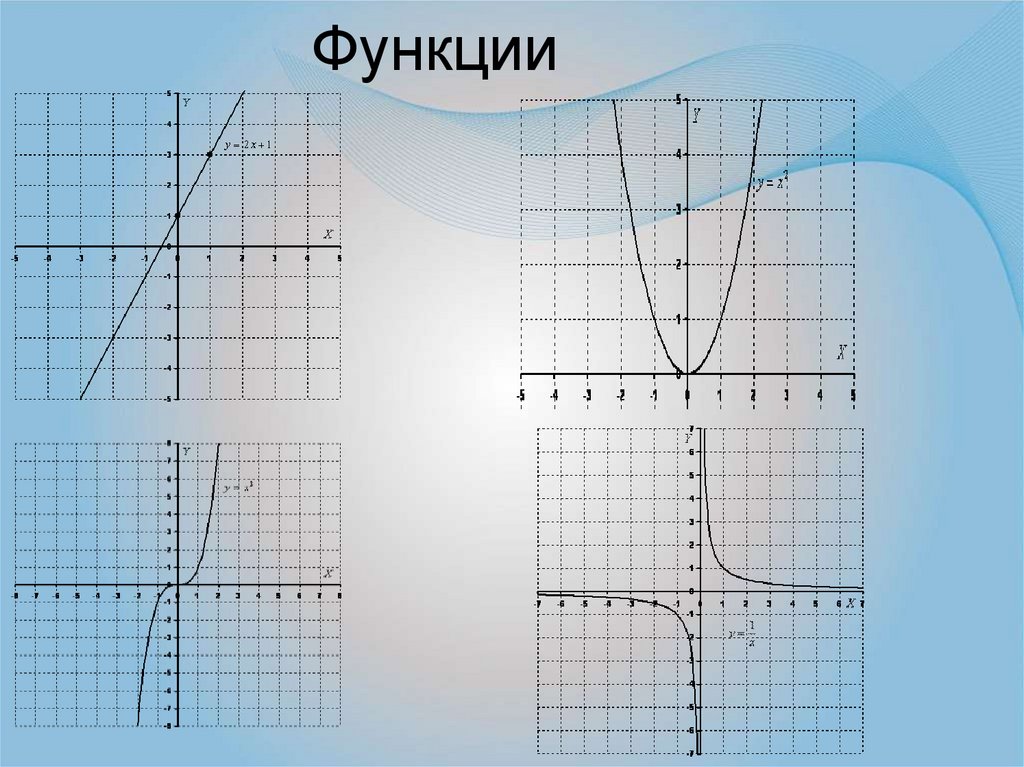
6. Функции

7.

Функция арифметического квадратного
корня
у х,
её свойства и график
у х

8. 1.Строить графики функции

у х, у х
у х n m
2.Решать графически уравнения
3.Находить наименьшее и
наибольшее значения функции
4.Определять принадлежность
точки графику
5.Определять принадлежность
переменной промежутку

9.

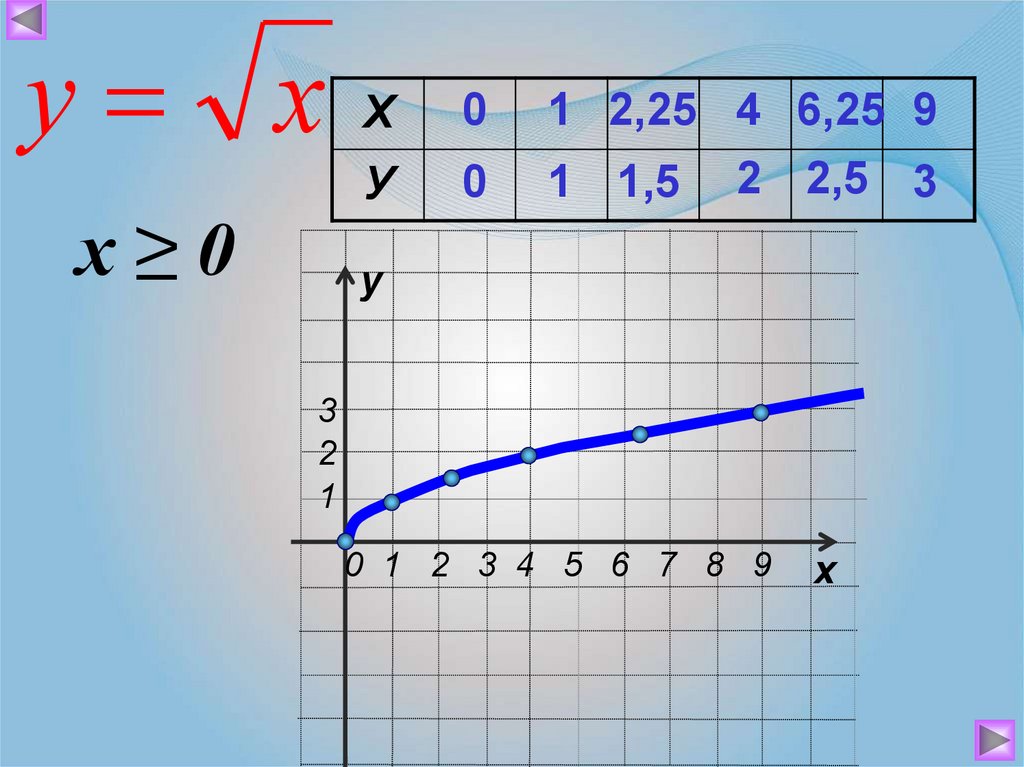
у х
х≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х

10.

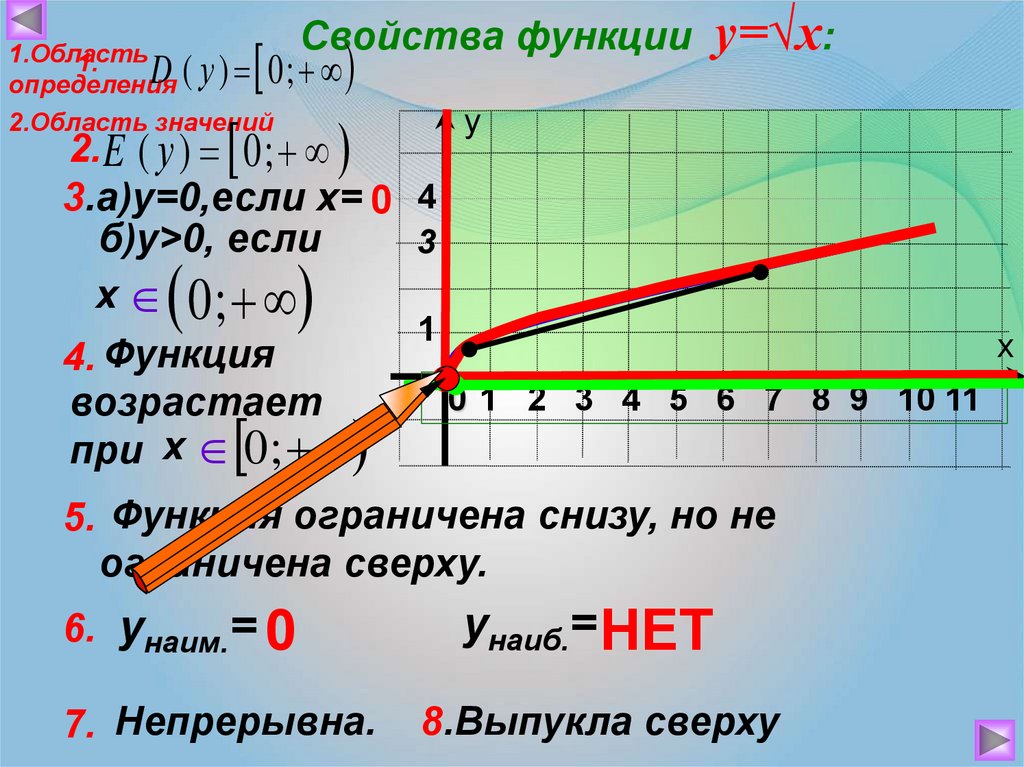
Свойства функции
D ( у ) 0;
1.Область
1.
определения
2.Область значений
у=√х:
у
2. E ( у ) 0 ;
3.а)у=0,если х= 0 4
б)у>0, если
3
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
5. Функция ограничена снизу, но не
ограничена сверху.
6. унаим.= 0
7. Непрерывна.
унаиб.= НЕТ
8.Выпукла сверху

11.

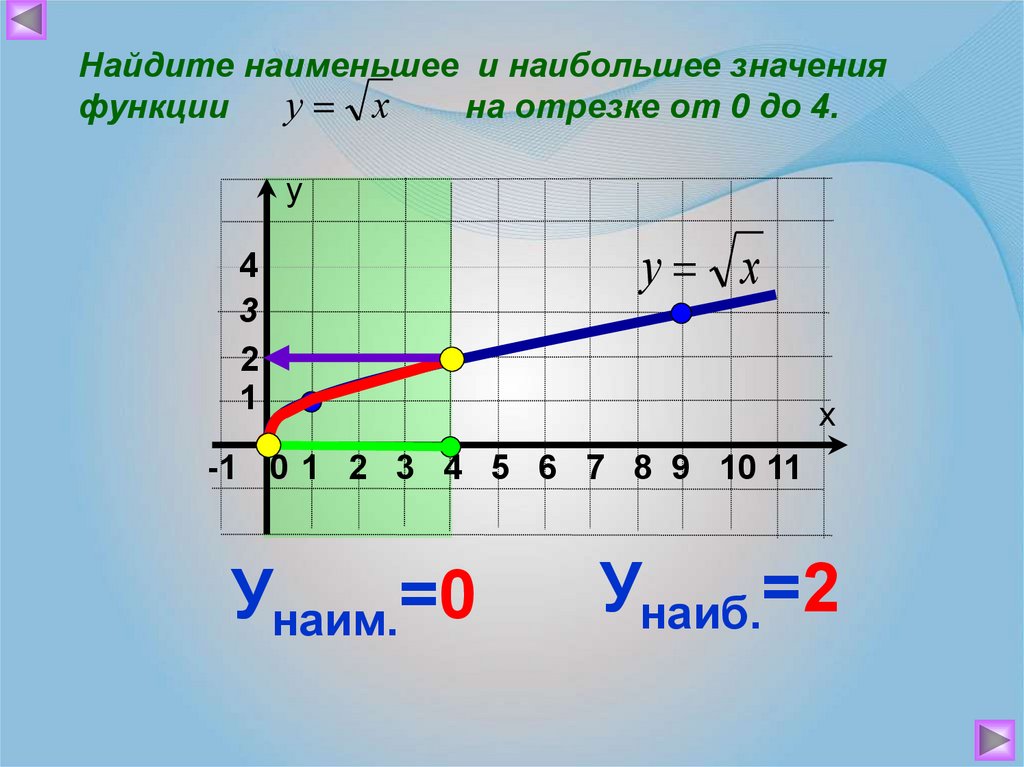
Найдите наименьшее и наибольшее значения
у х
функции
на отрезке от 0 до 4.
у
4
3
2
1
у х
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2