Решение задач с помощью систем уравнений второй степени

1. §7.Решение задач с помощью систем уравнений второй степени

Тема урока
§7.Решение задач с помощью
систем уравнений второй степени

2. 1) Периметр прямоугольника равен 80 см. Если основание прямоугольника увеличить на 8 см, а высоту – на 2 см, то площадь

прямоугольника увеличится
в полтора раза. Каковы стороны прямоугольника
Решение:
Пусть основание прямоугольника равно х см, а высота у см.
Периметр прямоугольника:
у см
Площадь прямоугольника:
2 х 2 у 80
ху
х см
1,5 ху
(у+2) см
2 х 2 у 80,
( х 8)( у 2) 1,5 ху.
Решив ее, найдем, что
(х+8) см
(28;12)или (24;16).
Ответ: стороны прямоугольника равны 28 см и 12 см или 24 см и 16 см.

3.

2) Сумма двух чисел равна 12, а их произведение равно 35.Найдите эти числа.
Решение. Пусть первое число х, а второе у.
х у 12,
у 12 х,
ху
35
.
х(12 х) 35.
у1 12 5 7;
х(12 х) 35.
12 х х 2 35
х 2 12 х 35 0
х1 х2 12, х1 5;
х2 7.
х1 х2 35.
у2 12 7 5;
Ответ: числа 5 и 7.

4. А

3) Диагональ прямоугольника равна 10см, а его периметр равен
28см. Найдите стороны прямоугольника.
В
у
С
х
А
АC =10см; P = 28см;
AB - ?
BС - ?
D
Пусть одна сторона х, а вторая - у.
2 х 2 у 28; : 2 х у 14;
2
2
2
2
2
х у 10 .
х у 100.
х 2 (14 х) 2 100.
х 2 196 28х х 2 100 0;
2 х 2 28х 96 0; : 2
х 2 14 х 48 0;
х1 х2 14; х1 6;
х2 8.
х1 х2 48.
у 14 х;
2
2
х
(
14
х
)
100.
у1 14 6 8;
у2 14 8 6.
(6;8) или (8;6).
Ответ. 6 см и 8 см.

5. А

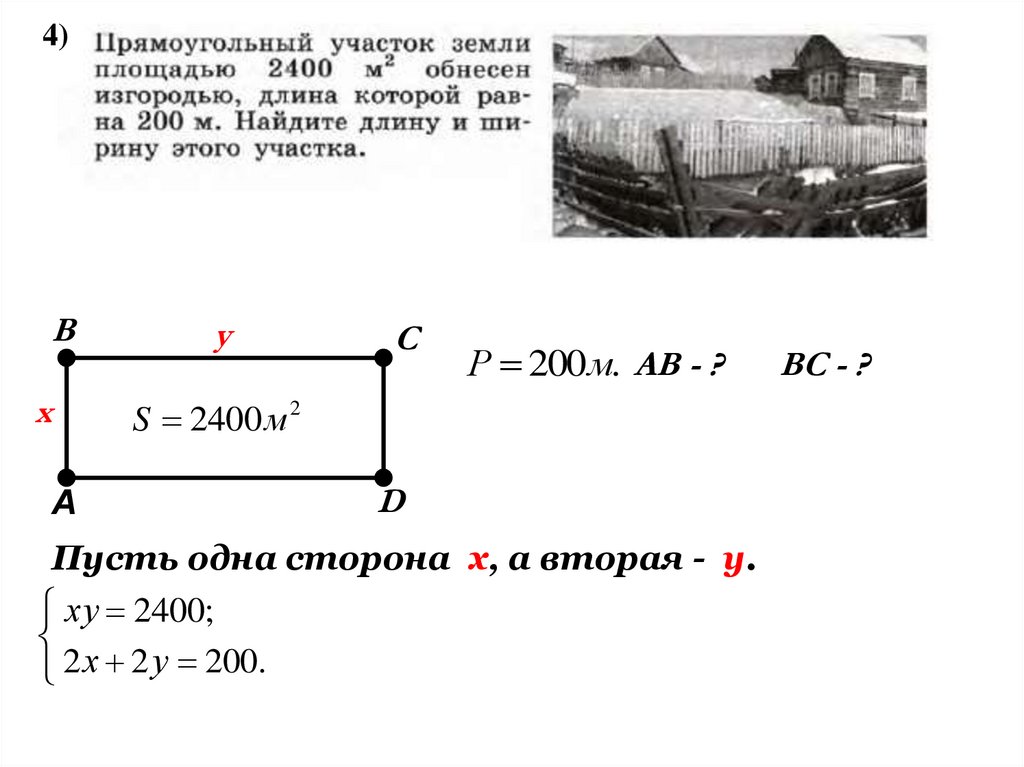
4)
В
х
у
С
Р 200м. AB - ?
S 2400м 2
А
D
Пусть одна сторона х, а вторая - у.
ху 2400;
2 х 2 у 200.
BС - ?