Алгебраический способ решения задач (часть 1)

1. УРАВНЕНИЯ

Алгебраический способ
решения задач (часть 1)
Домашнее задание
с.103 - 104 – читать; № 336(б), 337(б), 345(б).
Метапредмет – Задача

2. Цель нашего урока

- Понять сущность алгебраического метода решения задач.
- Составление уравнения по условию задачи
Великий математик Анри Пуанкаре сказал, что «математика это искусство давать различным вещам одно и то же
название». В этом шутливом афоризме заключён глубокий
смысл.
целеполагание

3. Алгебраический способ решения задач

Стр.103
Работа с учебником
Когда задачу решают алгебраическим способом, то
прежде всего условие задачи переводят на язык математики.
Основа такого перевода, его первый шаг — введение буквы
для обозначения какой-либо неизвестной величины.
В результате перевода обычно получается равенство,
содержащее букву. Это равенство, как вы уже знаете,
называют уравнением.
Организация и самоорганизация учащихся. Организация обратной связи

4. Алгебраический способ решения задач

Стр.103
Работа с учебником
В семье две пары близнецов, родившихся с
разницей в три года. В 2012 г. всем вместе исполнилось 50
лет. Сколько лет было каждому из близнецов в 2010 г.?
Арифметическое решение задачи:
Складывается возраст четверых детей. В 2010 г. возраст каждого из них на
2 года меньше, значит, их суммарный возраст меньше на 2 · 4 = 8 (лет).
Таким образом, в 2010 г. близнецам вместе было 50 – 8 = 42 (года).
Если бы все они были в возрасте младших, то в 2010 г. им было бы
вместе 42 – 3 · 2 = 36 (лет). Значит, младшим в 2010 г. было по
36 : 4 = 9 (лет), а старшим — по 9 + 3 = 12 (лет).
Организация и самоорганизация учащихся. Организация обратной связи

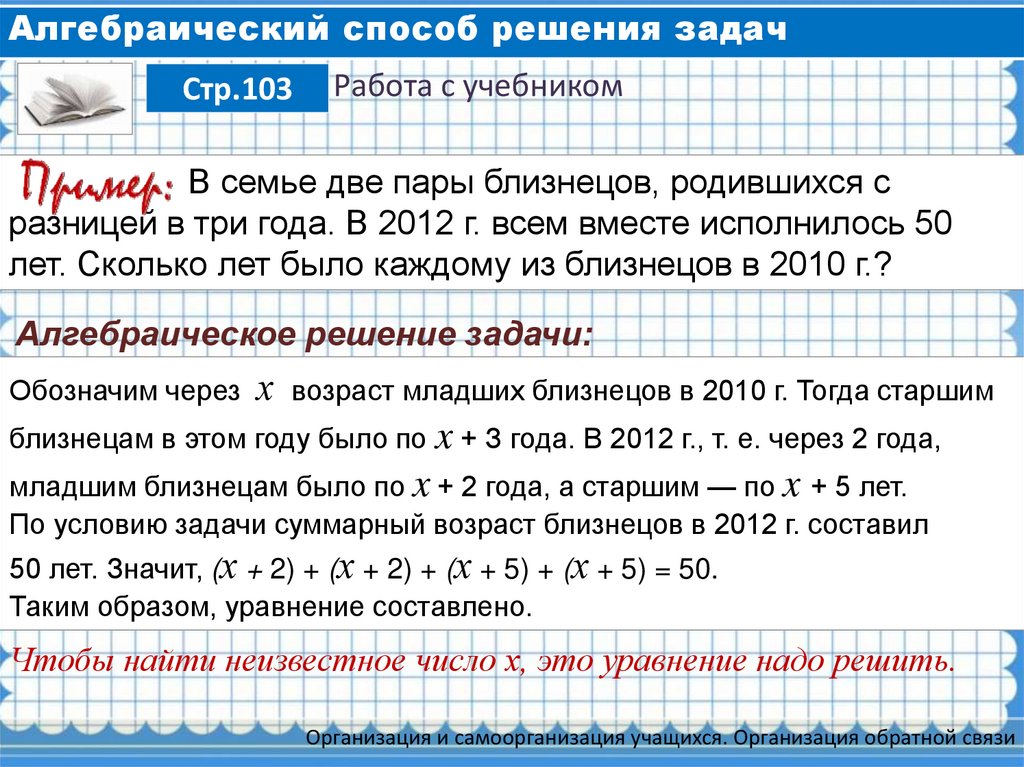
5. Алгебраический способ решения задач

Стр.103
Работа с учебником
В семье две пары близнецов, родившихся с
разницей в три года. В 2012 г. всем вместе исполнилось 50
лет. Сколько лет было каждому из близнецов в 2010 г.?
Алгебраическое решение задачи:
Обозначим через
х
возраст младших близнецов в 2010 г. Тогда старшим
близнецам в этом году было по x + З года. В 2012 г., т. е. через 2 года,
младшим близнецам было по x + 2 года, а старшим — по x + 5 лет.
По условию задачи суммарный возраст близнецов в 2012 г. составил
50 лет. Значит, (х + 2) + (х + 2) + (х + 5) + (х + 5) = 50.
Таким образом, уравнение составлено.
Чтобы найти неизвестное число х, это уравнение надо решить.
Организация и самоорганизация учащихся. Организация обратной связи

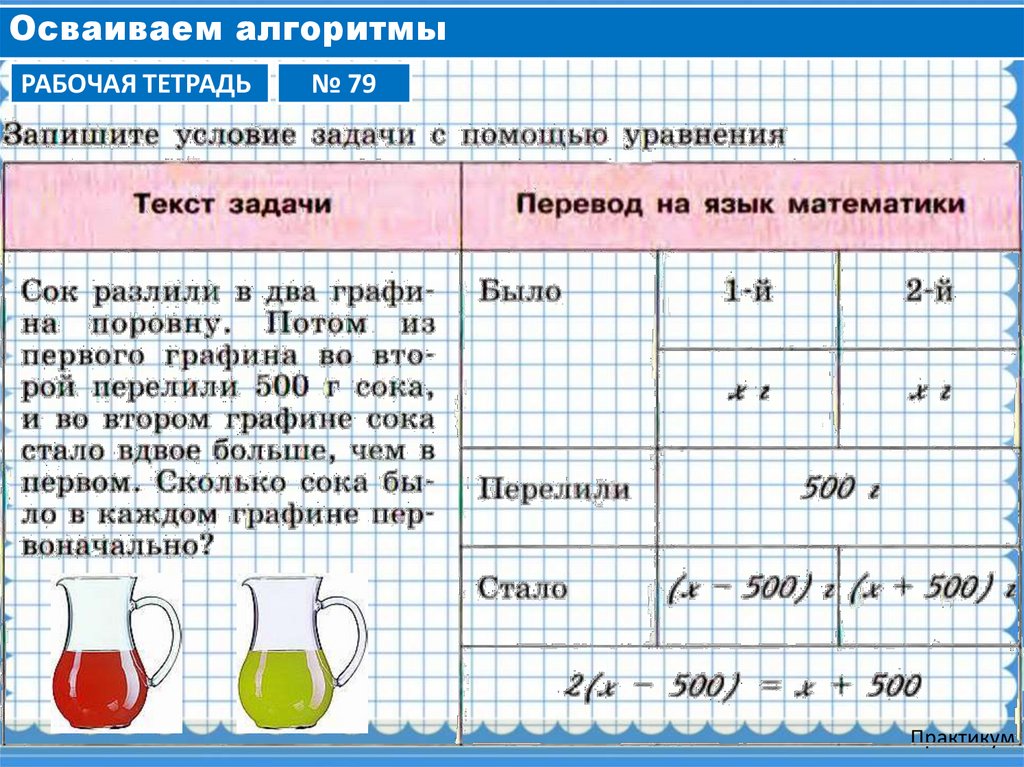
6. Осваиваем алгоритмы

РАБОЧАЯ ТЕТРАДЬ
№ 79
Практикум

7. Осваиваем алгоритмы

РАБОЧАЯ ТЕТРАДЬ
№ 80
x ор
x ор
12 ор
12 ор
(x – 12)ор (x + 12)ор
3(x – 12) = (x + 12)
?
Практикум

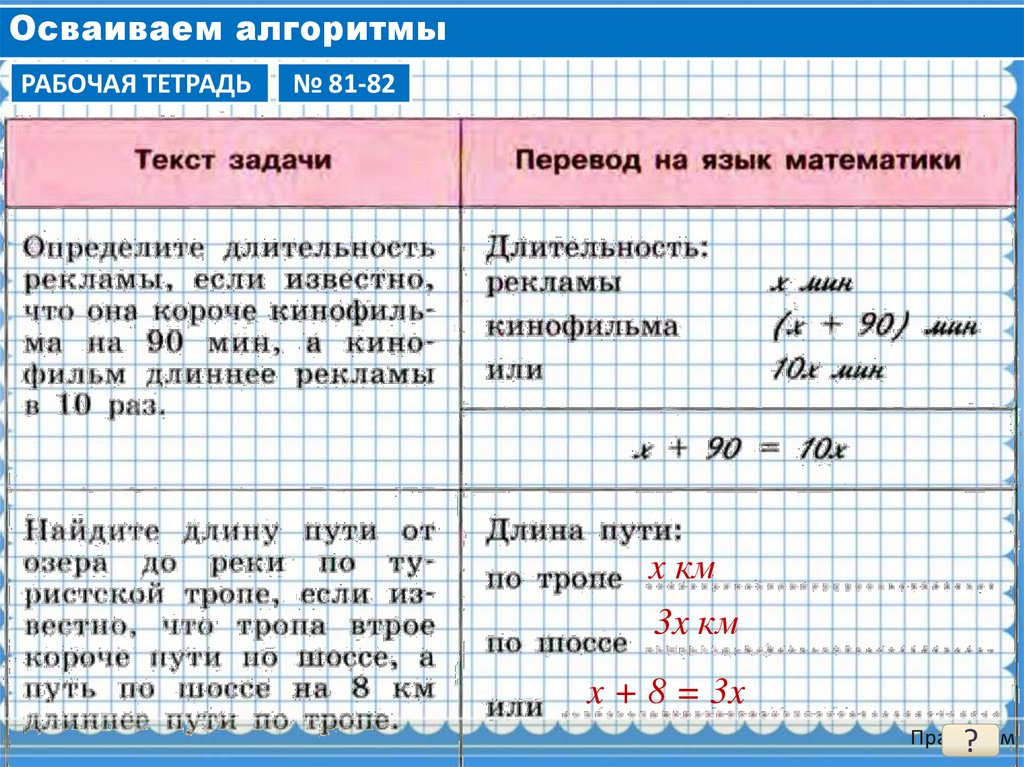
8. Осваиваем алгоритмы

РАБОЧАЯ ТЕТРАДЬ
№ 81-82
x км
3x км
x + 8 = 3x
Практикум
?

9. Составляем уравнение

УЧЕБНИК
№ 336(а)
Обозначим через х чел. – было в 1 вагоне,
тогда во 2 вагоне было (х + 14) чел.
По условию задачи число человек в двух вагонах
было равно 86.
Составим уравнение: х + (х + 14) = 86
1 уравнение
Обозначим через х чел. – было во 2 вагоне,
Составим уравнение: х + (х – 14) = 86
2 уравнение
Практикум

10. Составляем уравнение

УЧЕБНИК
№ 337(а)
Обозначим через х число листов в первой пачке,
тогда во 2 пачке было 4х листов.
По условию задачи число листов в двух пачках
было равно 350.
Составим уравнение: х + 4х = 350
1 уравнение
Обозначим через х число листов во второй пачке
Составим уравнение: х + х:4 = 350
2 уравнение
Практикум

11. Составляем уравнение

УЧЕБНИК
№ 343
Обозначим через х лет возраст Пети,
тогда возраст отца составляет 3х лет, а
возраст деда 6х лет.
По условию задачи суммарный возраст Пети,
отца и деда составляет 110лет.
Значит, 6х + 3х + х = 110
1 уравнение
Составим уравнение: 110 – (6х + 3х) = х
2 уравнение
Составим уравнение: 110 – 6х = 3х + х
3 уравнение
Практикум

12. Составляем уравнение

УЧЕБНИК
№ 345
уравнение
(х + 11) : 2 = х + 2
УЧЕБНИК
№ 338
верно
верно
Практикум

13. Составление уравнений

Дидактические материалы
(х + 3) + х = 21;
х + 1,5х = 15;
С.38
21 – (х + 3) = х;
15 – 1,5х = х;
1
2
Практикум

14. Составление уравнений

Дидактические материалы
65х + 53(х – 2 ) = 602;
С.38
602 – 65х = 53(х – 2);
3
Проверка полученных результатов. Коррекция