Похожие презентации:
Сфера и шар
1. Тема урока: «Сфера и шар.»
14.12.2021г2. Цели: ввести понятие сферы, шара и их элементов; вывести уравнение сферы в заданной прямоугольной системе координат;
Цели: ввести понятие сферы, шара и их элементов; вывестиуравнение сферы в заданной прямоугольной системе координат;
исследовать взаимное расположение сферы и плоскости.
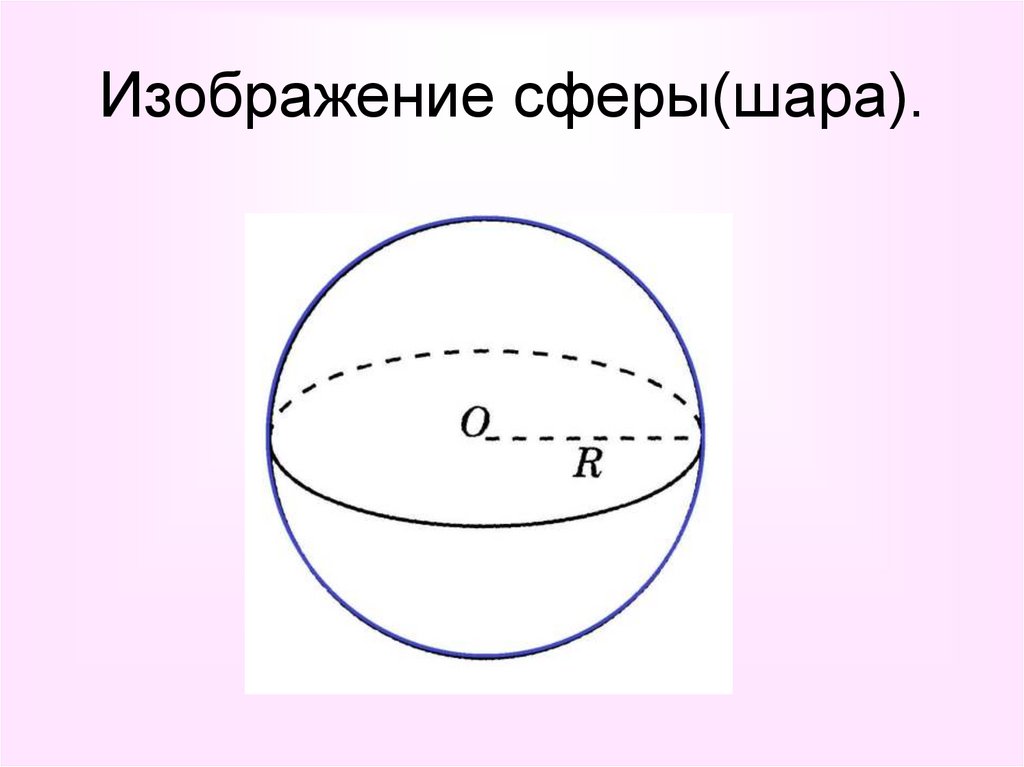
3. Изображение сферы(шара).
4.
Сферой называетсяповерхность, которая
состоит из всех точек
пространства,
находящихся на заданном
расстоянии от данной
точки. Эта точка
называется центром, а
заданное расстояние –
радиусом сферы, или шара
– тела, ограниченного
сферой. Шар состоит из
всех точек пространства,
находящихся на
расстоянии не более
заданного от данной
точки.
5.
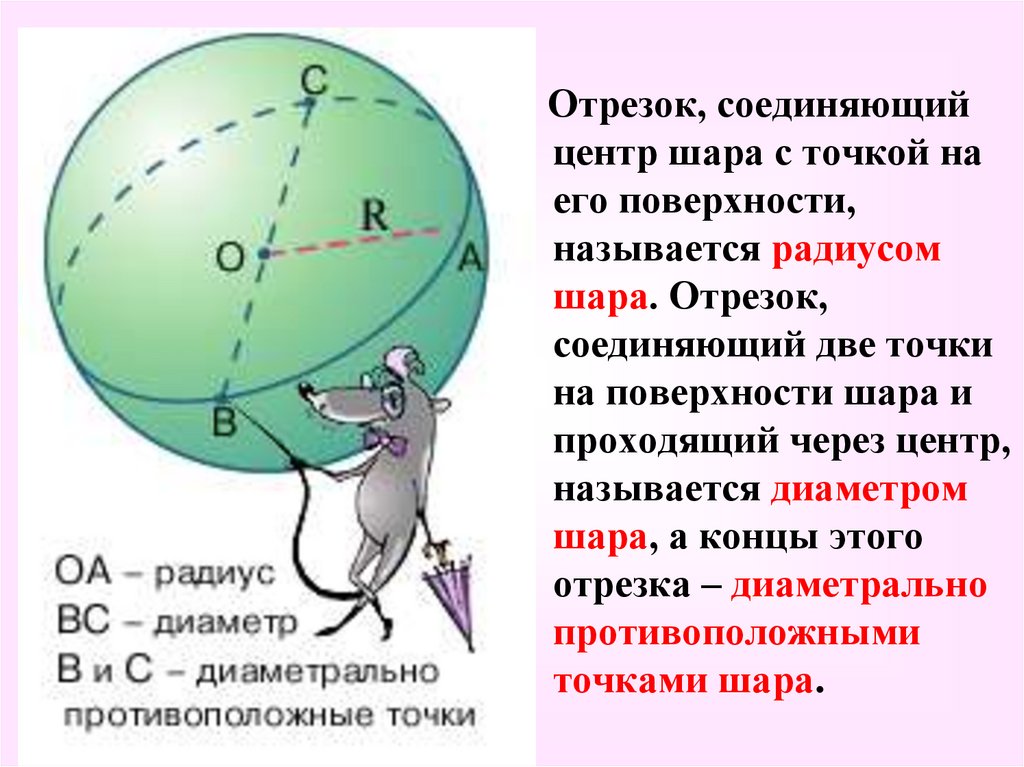
Отрезок, соединяющийцентр шара с точкой на
его поверхности,
называется радиусом
шара. Отрезок,
соединяющий две точки
на поверхности шара и
проходящий через центр,
называется диаметром
шара, а концы этого
отрезка – диаметрально
противоположными
точками шара.
6.
?Чему равно
расстояние между
диаметрально
противоположными
точками шара, если
известна
удаленность точки,
лежащей на
поверхности шара от
центра?
18
7.
Шар можнорассматривать как
тело, полученное от
вращения полукруга
вокруг диаметра как
оси.
8.
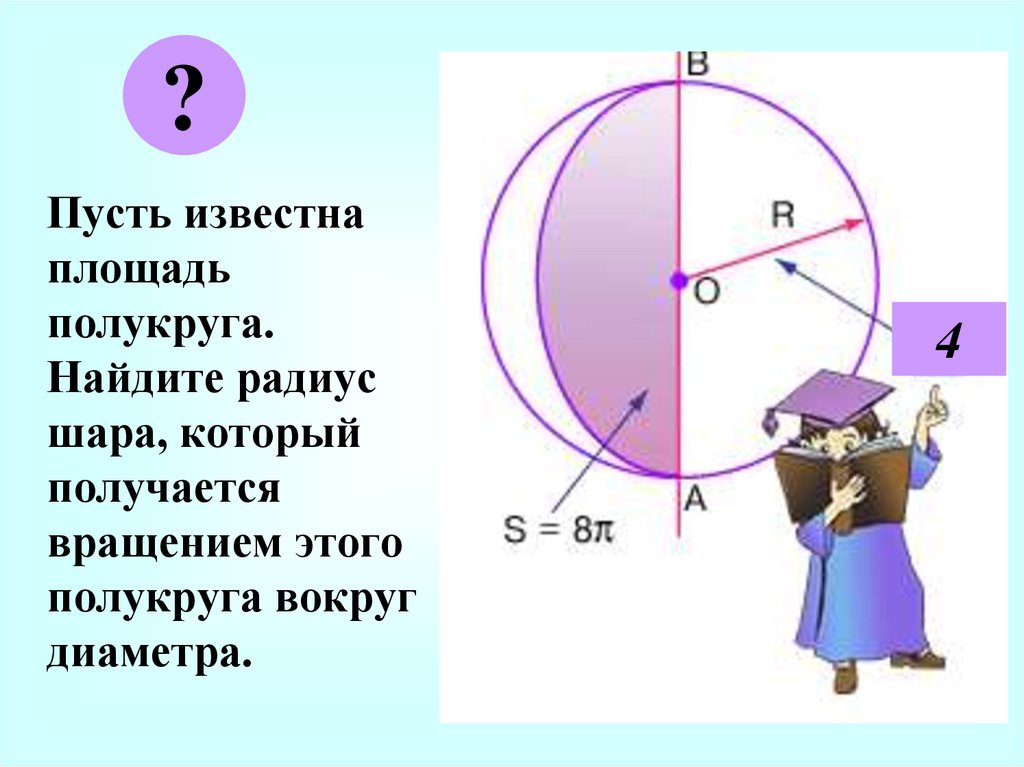
?Пусть известна
площадь
полукруга.
Найдите радиус
шара, который
получается
вращением этого
полукруга вокруг
диаметра.
4
9. Уравнение сферы.
10.
11. Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в
центрэтого круга.
Дано:
шар O, R
секущая плоскость
ОО1
Доказать:
сечение круг
О1 центр круга
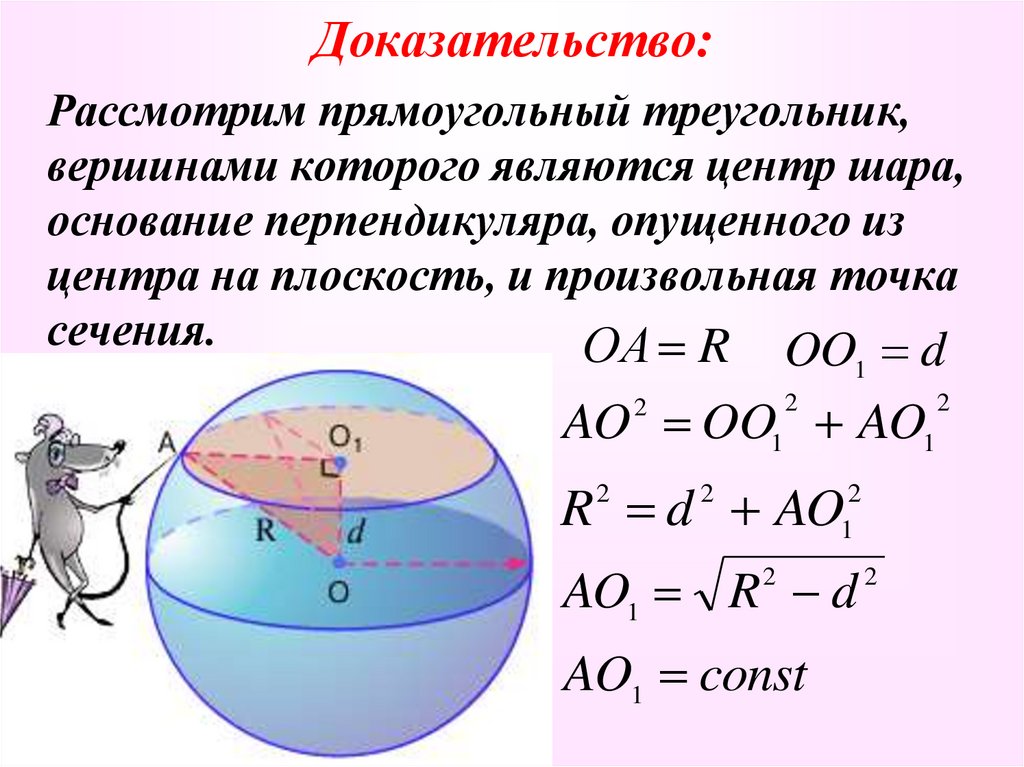
12. Доказательство:
Рассмотрим прямоугольный треугольник,вершинами которого являются центр шара,
основание перпендикуляра, опущенного из
центра на плоскость, и произвольная точка
сечения.
ОА R OO d
1
AO OO1 AO1
2
2
R d AO
2
2
2
1
AO1 R d
2
AO1 const
2
2
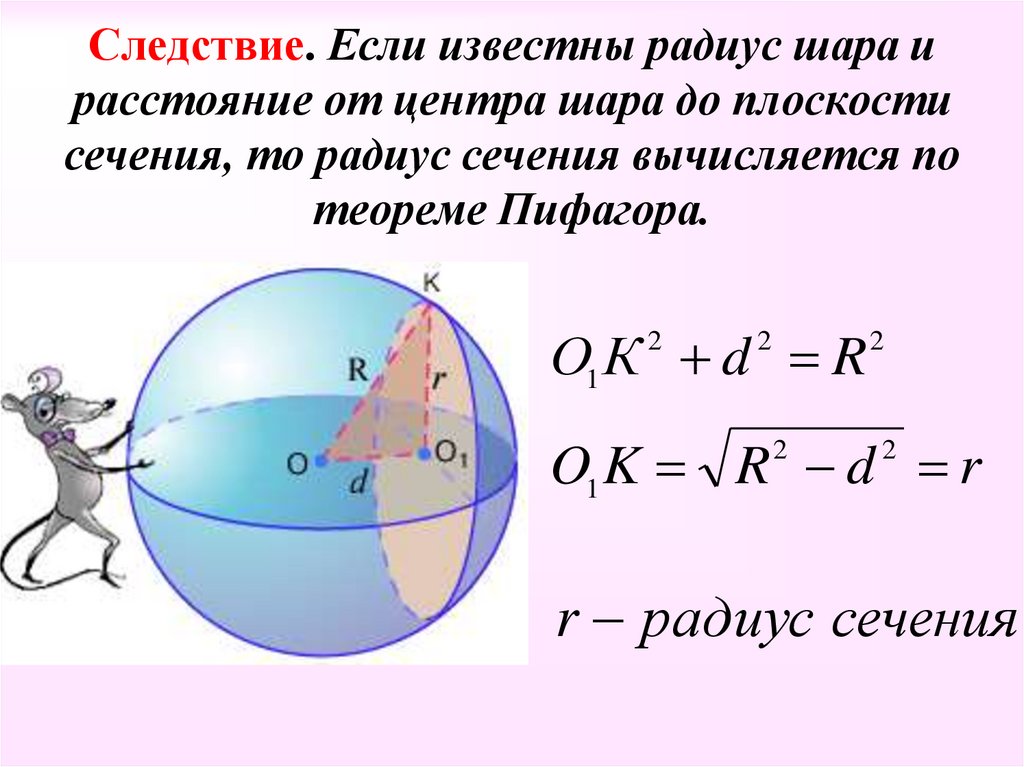
13. Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме
Пифагора.О1 К d R
2
2
2
O1 K R d r
2
2
r радиус сечения
14.
?Пусть известны
диаметр шара и
расстояние от центра
шара до секущей
плоскости. Найдите
радиус круга,
получившегося
сечения.
10
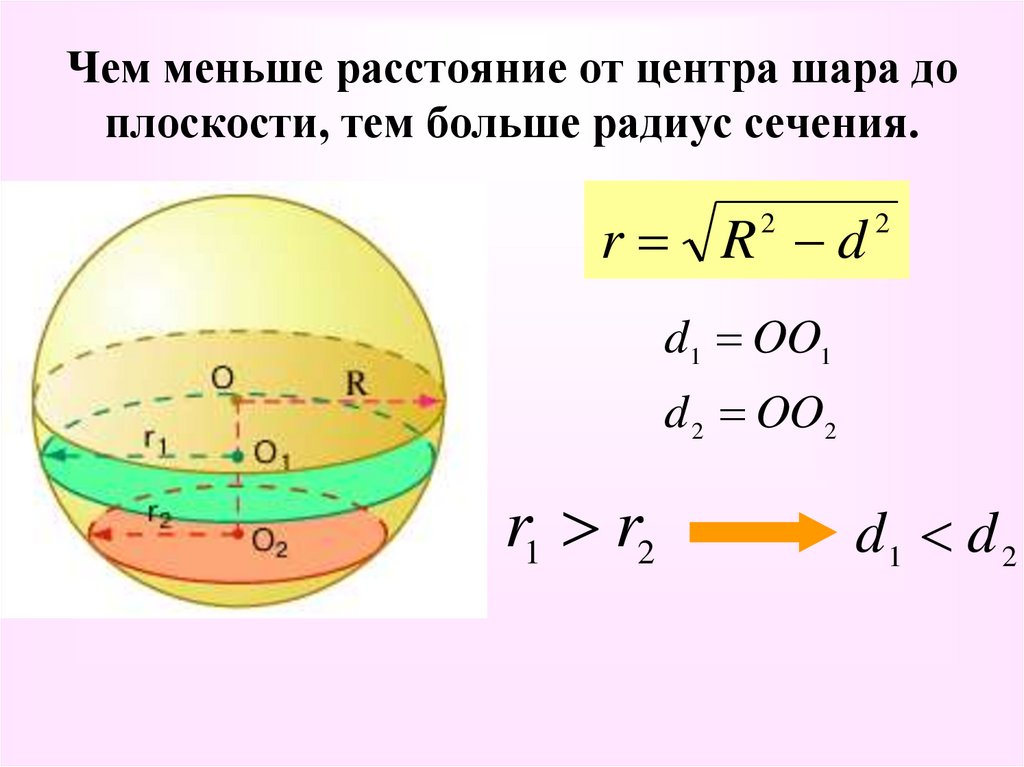
15. Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.
r R d2
2
d1 OO1
d 2 OO2
r1 r2
d1 d 2
16. Итог урока Сегодня вы познакомились с:
определением сферы, шара;уравнением окружности;
знаем, что любое сечение шара
плоскостью есть круг.
17. Домашнее задание:
1)Записать уравнение сферы, если даныкоординаты центра(2;3;-1) и точки,
лежащей на сфере (-4;6;2).
2)Шар, радиуса 13 см, пересечён
плоскостью на расстоянии 5 см от
центра шара. Найдите площадь
сечения.
3) №573(а)(новый № 373(а))
18. Заключение
• На этом наш урок закончен• Спасибо за работу












 Математика
Математика








