Свойства функций

1.

Свойства функций

2.

Определите, какой из данных графиков
является графиком функции
Рис.1
Рис.2
Рис.3
у
у
х
Рис.4
у
х
у
х
НЕ ЯВЛЯЮТСЯ графиками функций рис.1, рис. 3,рис. 4
х

3.

Область определения
Область определения функции – все
значения, которые принимает
независимая переменная.
Обозначается : D (f).
Пример. Функция задана формулой у =
6
х 2 9
Данная формула имеет смысл при всех значениях
х ≠ -3, х ≠ 3,
поэтому D( y )=(- ∞;-3) U (-3;3) U (3; +∞)

4.

Область определения функции
Все допустимые значения
аргумента x функции y(х).
назад

5.

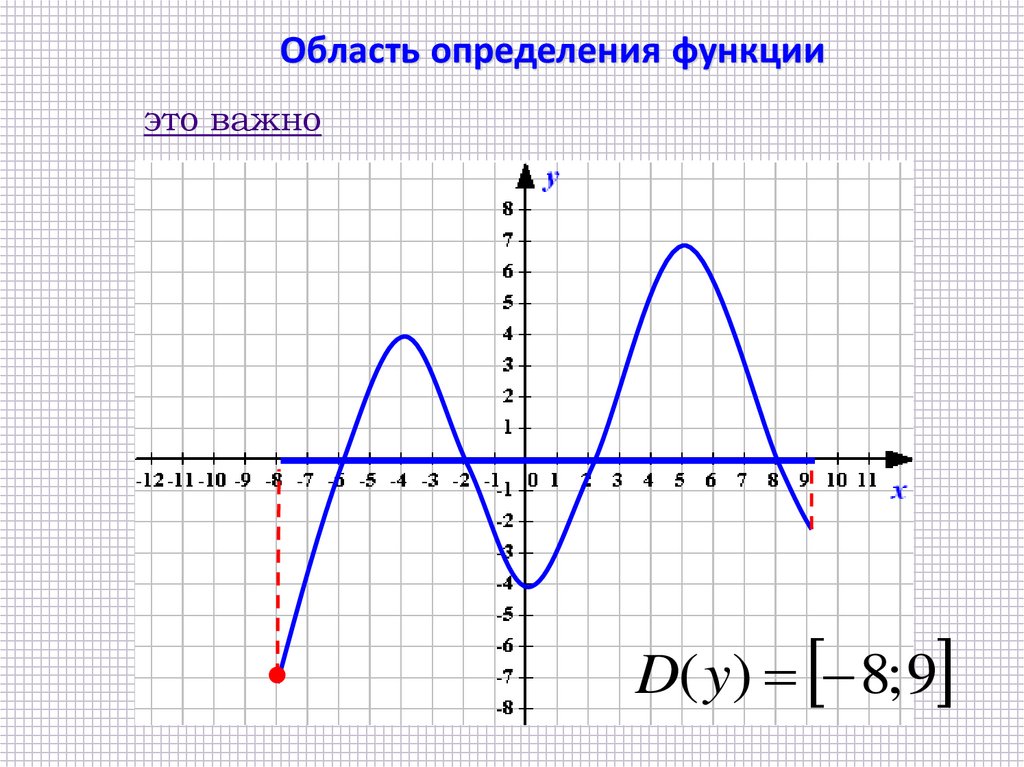
Область определения функции
это важно
D( y) 8; 9

6.

Область значений
Область значений функции – все
значения, которые принимает
зависимая переменная.
Обозначается : E (f)
Пример. Функция задана формулой у =
х 9
2
Данная функция является квадратичной , график – парабола,
вершина (0; 9)
поэтому E( y )= [ 9 ; +∞)

7.

Область значения функции
Множество, состоящее из всех чисел
y(x), таких, что x принадлежит
области определения функции y(х).

8.

Область значений функции
это важно
E( y) 7; 7

9.

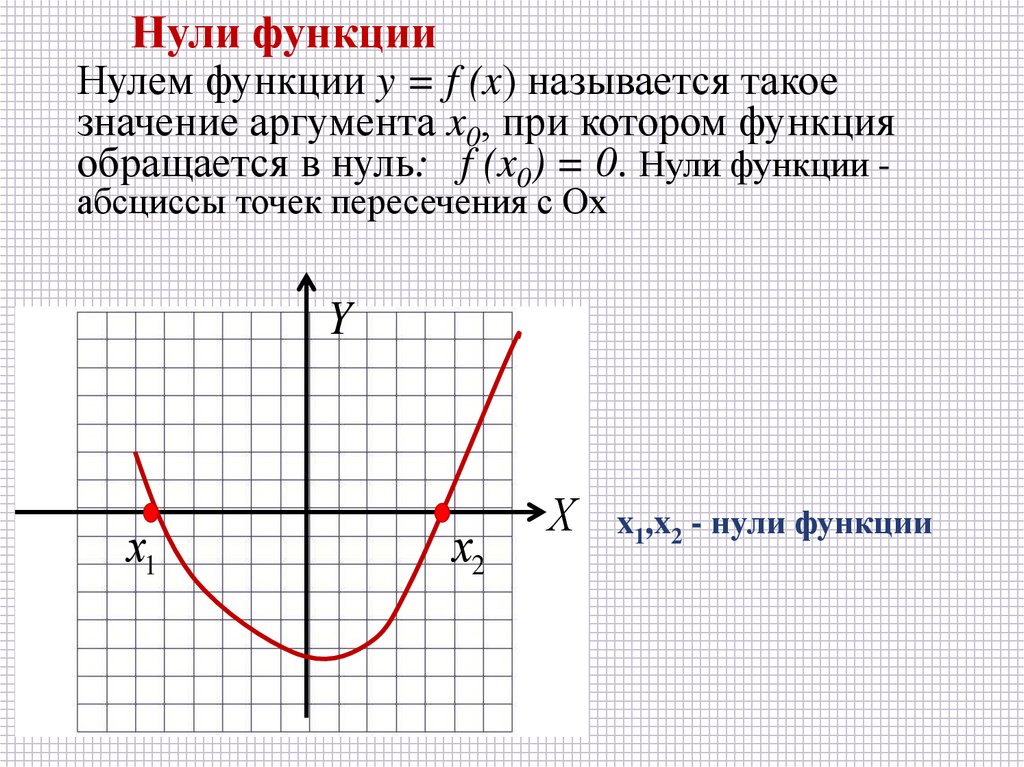
Нули функции
Нулем функции y = f (x) называется такое
значение аргумента x0, при котором функция
обращается в нуль: f (x0) = 0. Нули функции абсциссы точек пересечения с Ох
Y
х1
х2
Х
x1,x2 - нули функции

10.

Нули функции
это важно
x 6; x 2;
x 2; x 8

11.

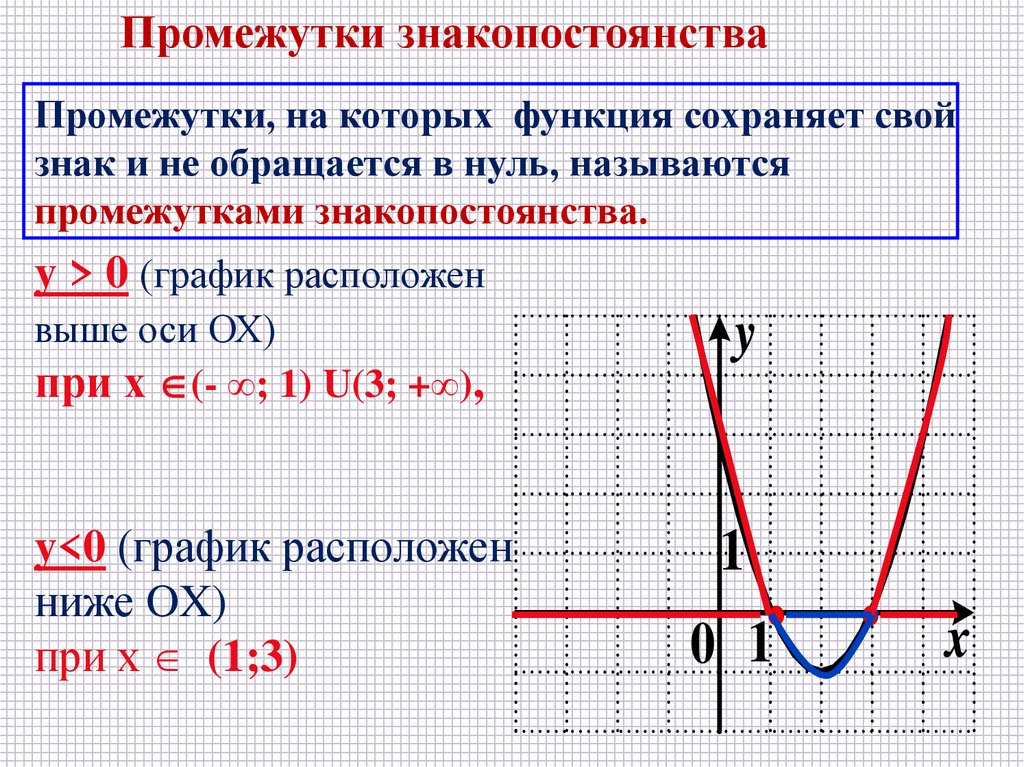
Промежутки знакопостоянства
Промежутки, на которых функция сохраняет свой
знак и не обращается в нуль, называются
промежутками знакопостоянства.
y > 0 (график расположен
выше оси ОХ)
при х (- ∞; 1) U(3; +∞),
y<0 (график расположен
ниже OX)
при х (1;3)
y
1
0 1
x

12.

Промежутки знакопостоянства
функции
Это промежутки, на которых функция
y(х) принимает положительные
(отрицательные) значения.

13.

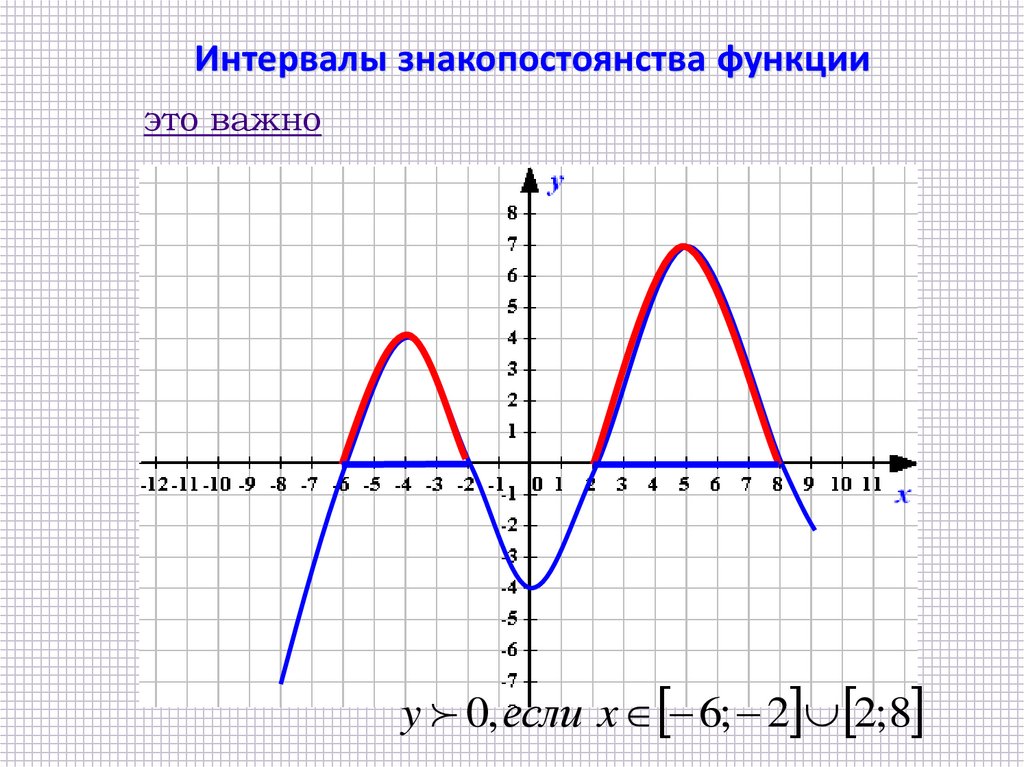
Интервалы знакопостоянства функции
это важно
y 0, если x 6; 2 2; 8

14.

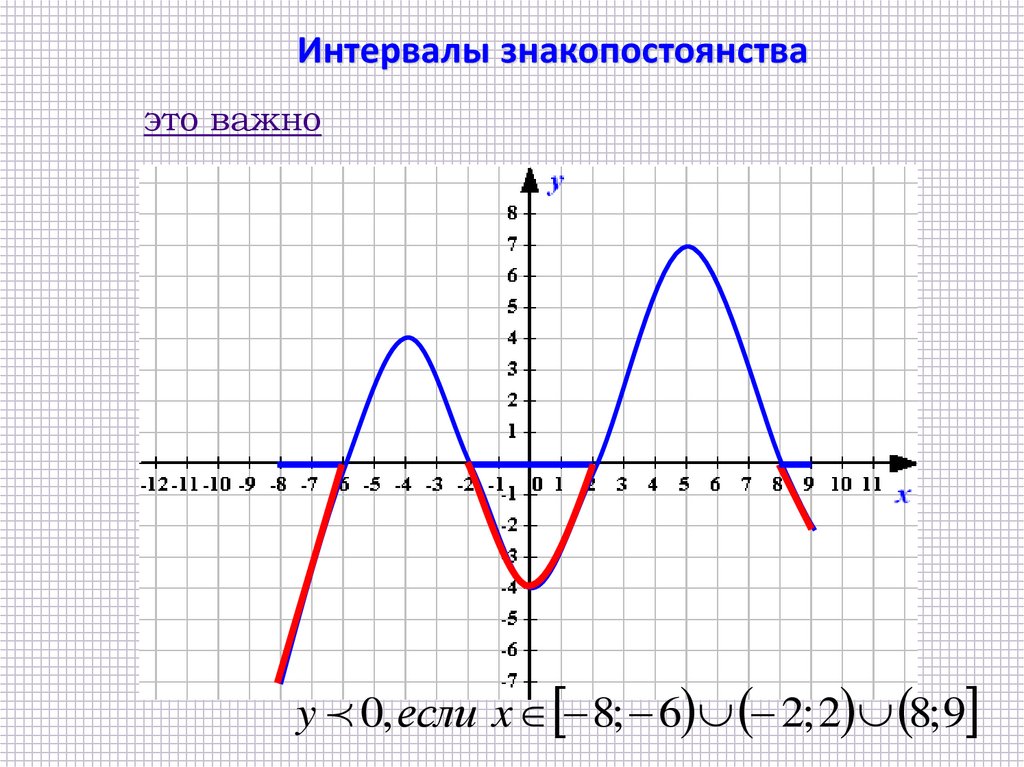
Интервалы знакопостоянства
это важно
y 0, если x 8; 6 2; 2 8; 9

15.

Возрастание и убывание функции
Функцию у = f(х) называют
убывающей на множестве Х,
если для любых двух точек
х1 и х2 из области определения,
таких, что х1 < х2, выполняется
неравенство
f(х1) >f(х2) .
Функцию у = f(х) называют
возрастающей на множестве
Х, если для любых двух
точек х1 и х2 из области
определения, таких, что х1 < х2,
выполняется неравенство
f(х1) < f(х2) .
f(x2)
f(x1)
f(x1)
x1
f(x2) х1
x2
x2
x1
x2

16.

Монотонность функции
Функция y(х) убывает на множестве P, если для
любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) < y (x1)
Функция y(х) возрастает на множестве P, если
для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)

17.

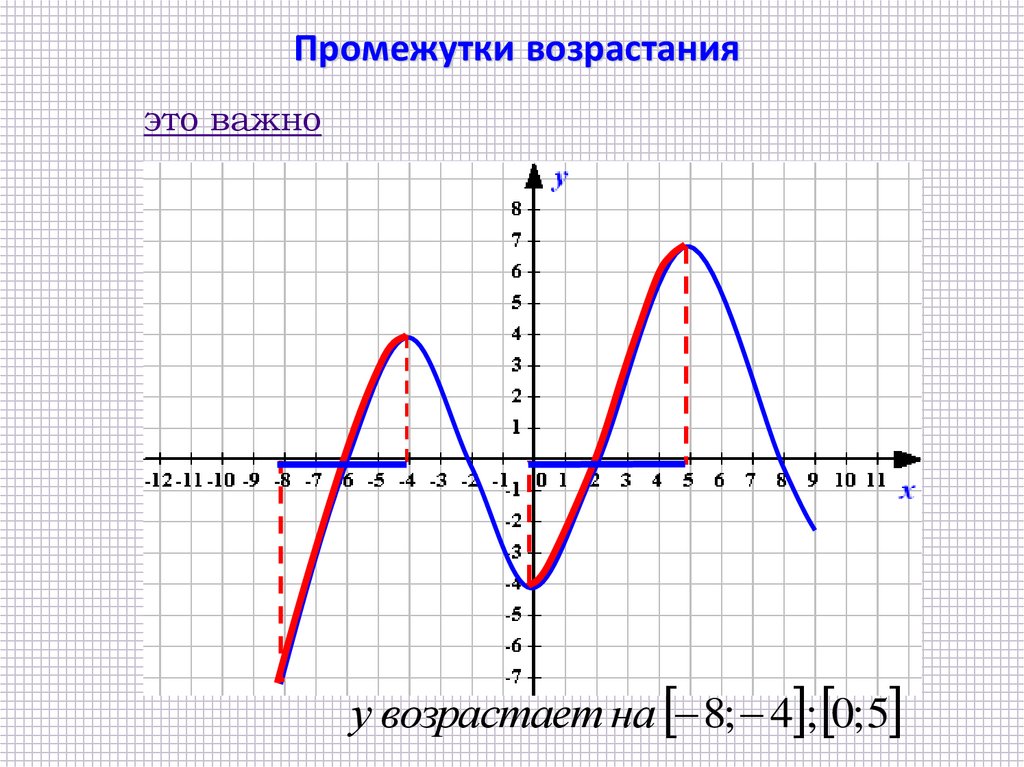
Промежутки возрастания
это важно
у возрастает на 8; 4 ; 0; 5

18.

Промежутки убывания
это важно
у убывает на 4; 0 ; 5; 9

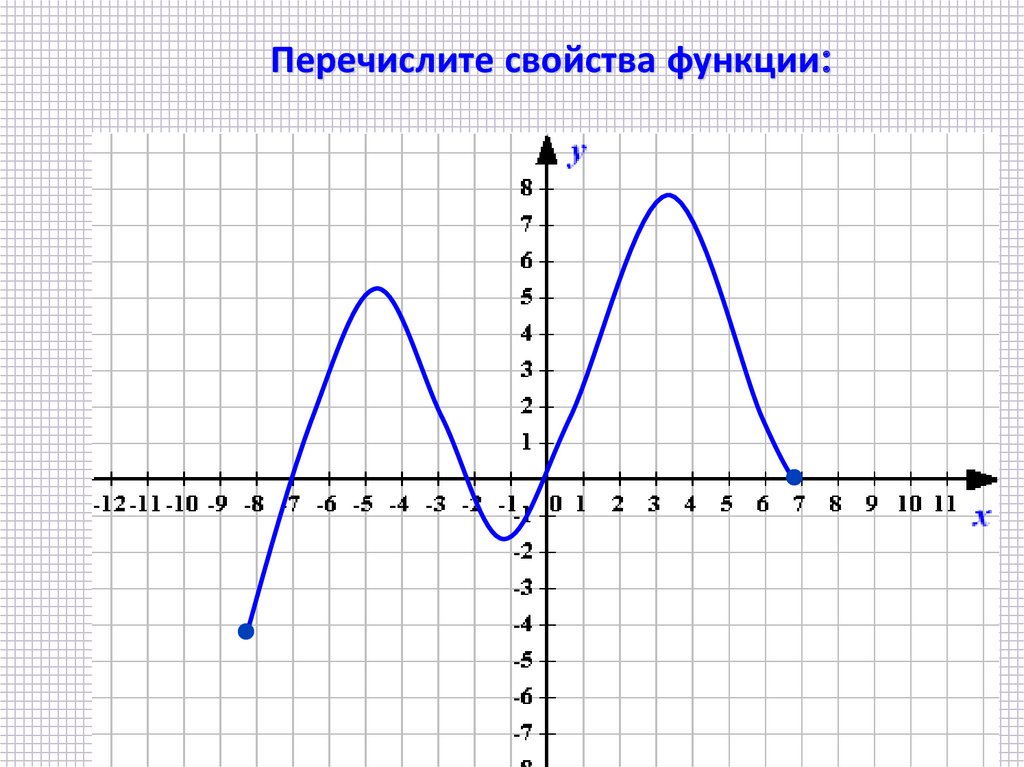
19. Алгоритм исследования функции:

1.
2.
3.
4.
5.
1. Область определения функции
2. Множество значений функции
3. Нули функции
4. Промежутки знакопостоянства (f(x)>0;
f(x)<0)
5. Монотонность (промежутки
возрастания, убывания)

20.

Перечислите свойства функции: