Похожие презентации:
Свойства функции
1.
17.09п2Свойства
функции.
А-9
2.
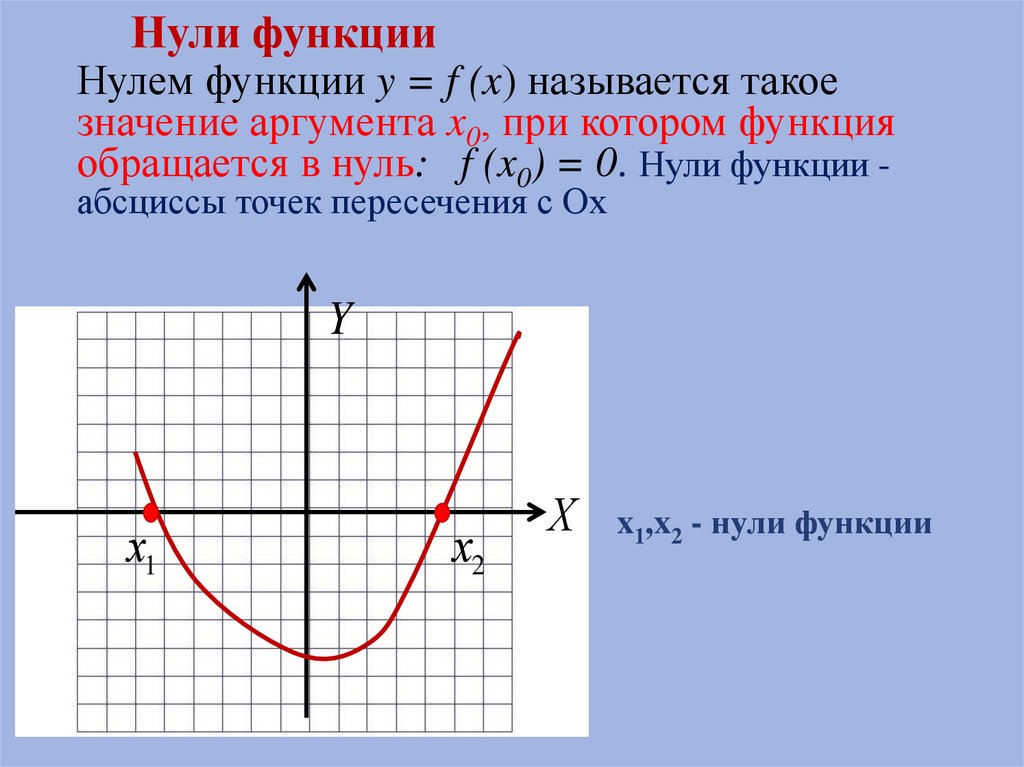
Нули функцииНулем функции y = f (x) называется такое
значение аргумента x0, при котором функция
обращается в нуль: f (x0) = 0. Нули функции абсциссы точек пересечения с Ох
Y
х1
х2
Х
x1,x2 - нули функции
3.
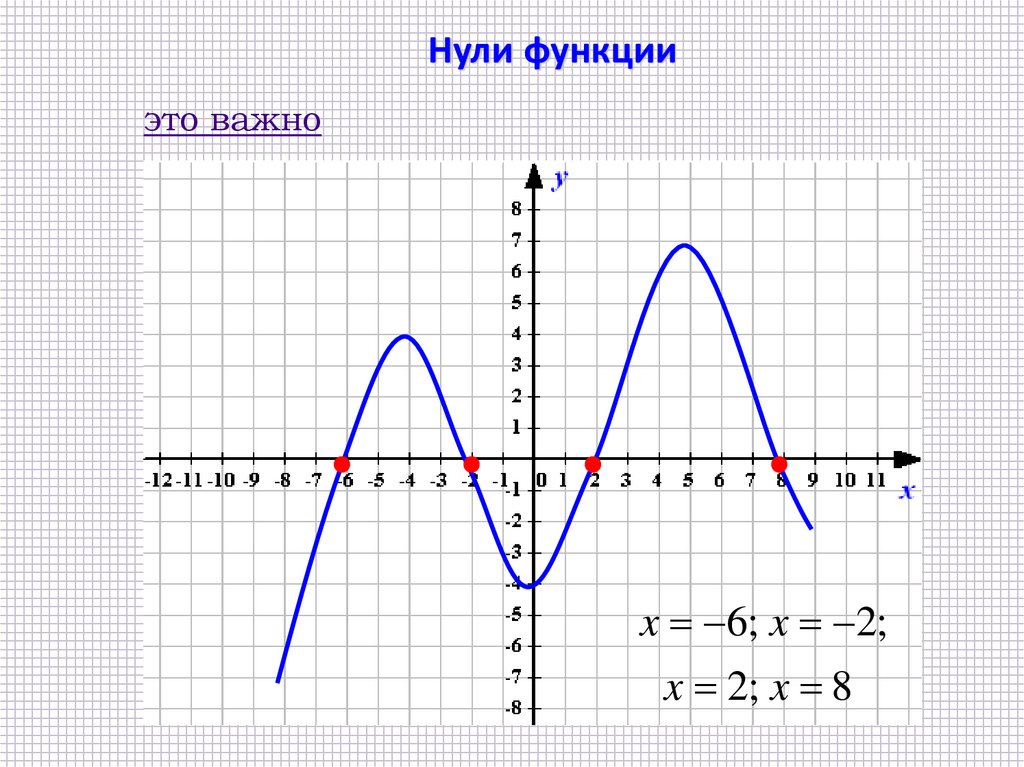
Нули функцииэто важно
x 6; x 2;
x 2; x 8
4.
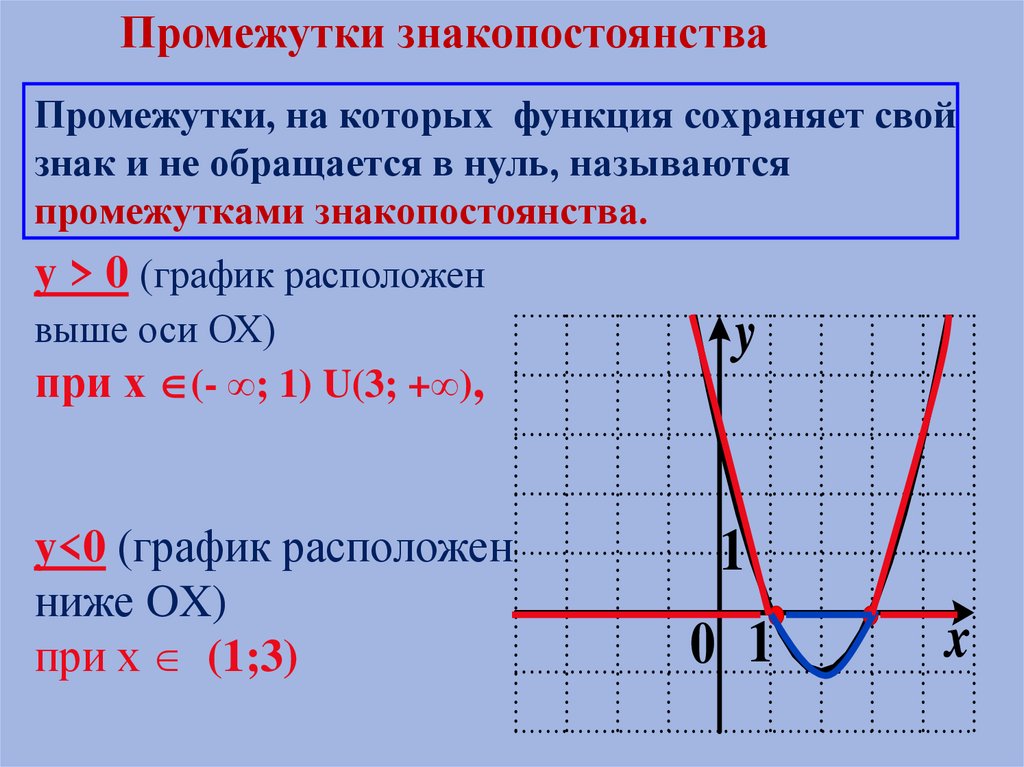
Промежутки знакопостоянстваПромежутки, на которых функция сохраняет свой
знак и не обращается в нуль, называются
промежутками знакопостоянства.
y > 0 (график расположен
выше оси ОХ)
при х (- ∞; 1) U(3; +∞),
y<0 (график расположен
ниже OX)
при х (1;3)
y
1
0 1
x
5.
Промежутки знакопостоянствафункции
Это промежутки, на которых функция
y(х) принимает положительные
(отрицательные) значения.
6.
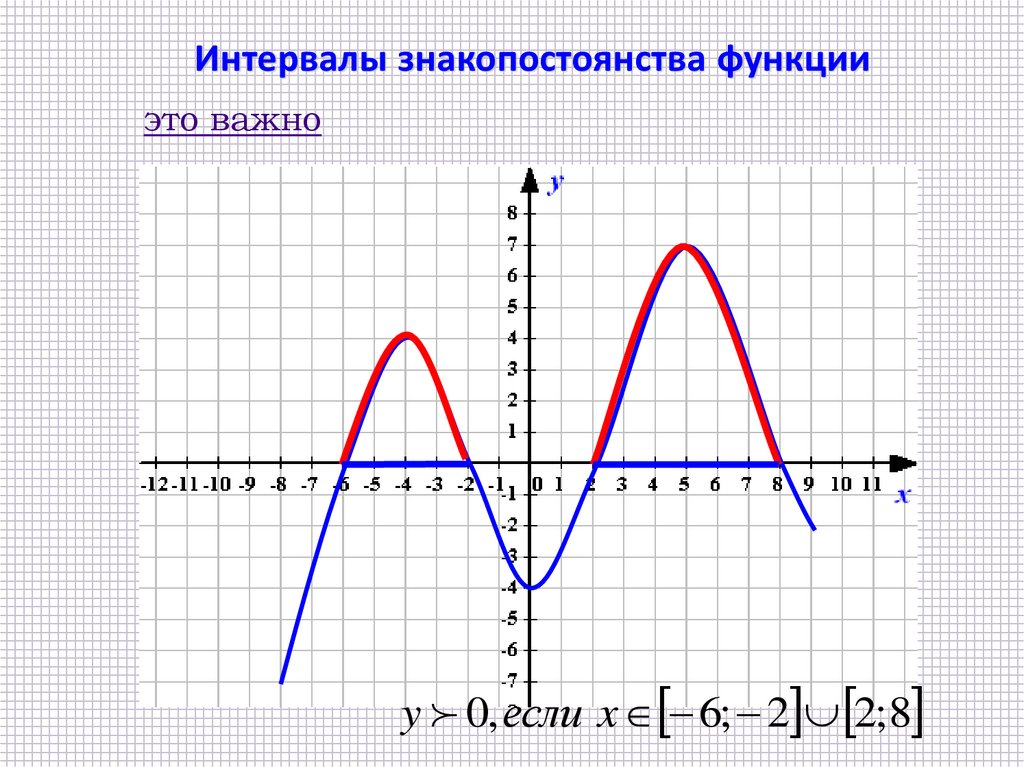
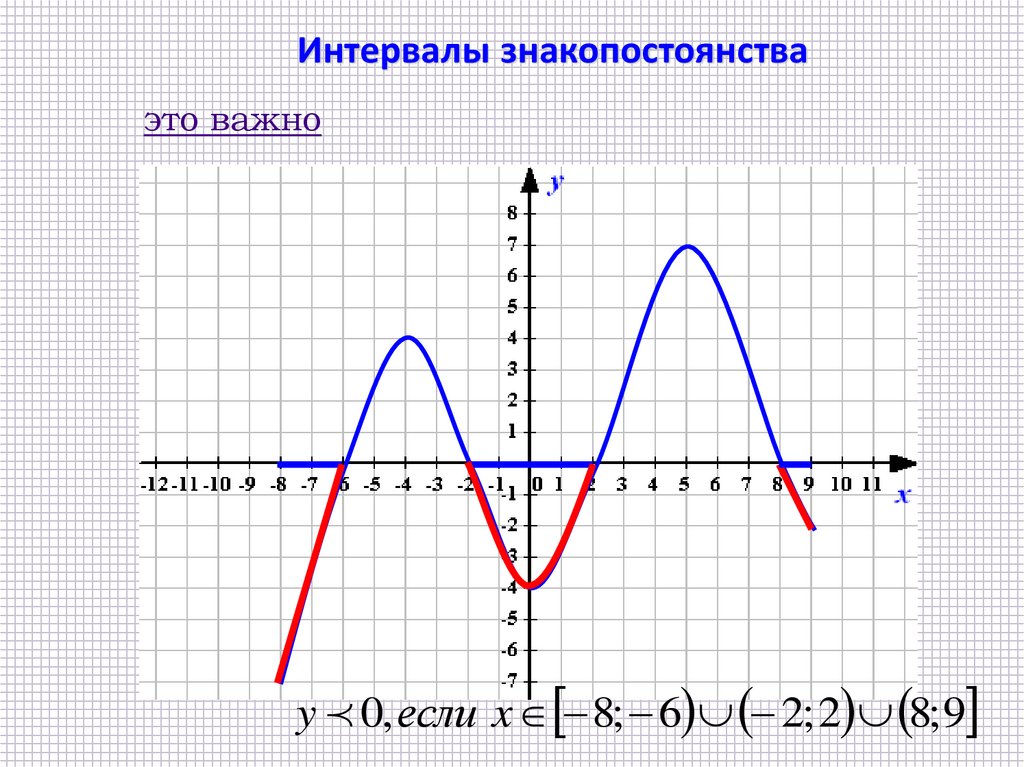
Интервалы знакопостоянства функцииэто важно
y 0, если x 6; 2 2; 8
7.
Интервалы знакопостоянстваэто важно
y 0, если x 8; 6 2; 2 8; 9
8.
Монотонность функцииФункцию у = f(х) называют
убывающей на множестве Х,
если для любых двух точек
х1 и х2 из области определения,
таких, что х1 < х2, выполняется
неравенство
f(х1) >f(х2) .
Функцию у = f(х) называют
возрастающей на множестве
Х, если для любых двух
точек х1 и х2 из области
определения, таких, что х1 < х2,
выполняется неравенство
f(х1) < f(х2) .
f(x2)
f(x1)
f(x1)
x1
f(x2) х1
x2
x2
x1
x2
9.
Монотонность функцииФункция y(х) убывает на множестве P, если для
любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) < y (x1)
Функция y(х) возрастает на множестве P, если
для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)
10.
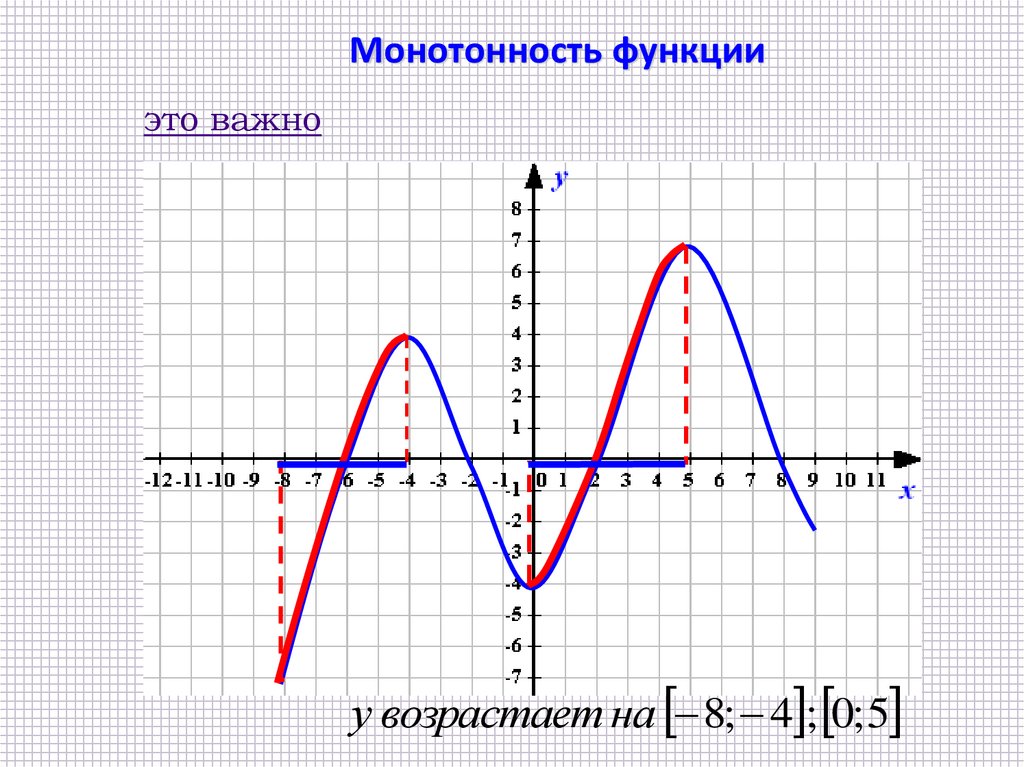
Монотонность функцииэто важно
у возрастает на 8; 4 ; 0; 5
11.
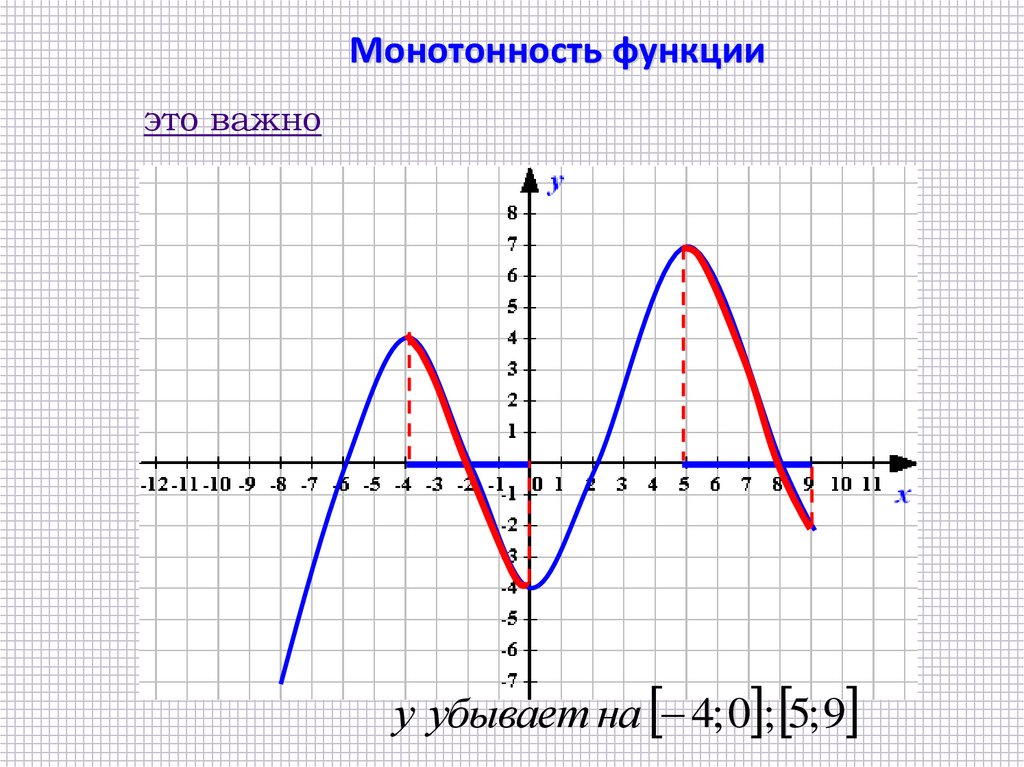
Монотонность функцииэто важно
у убывает на 4; 0 ; 5; 9
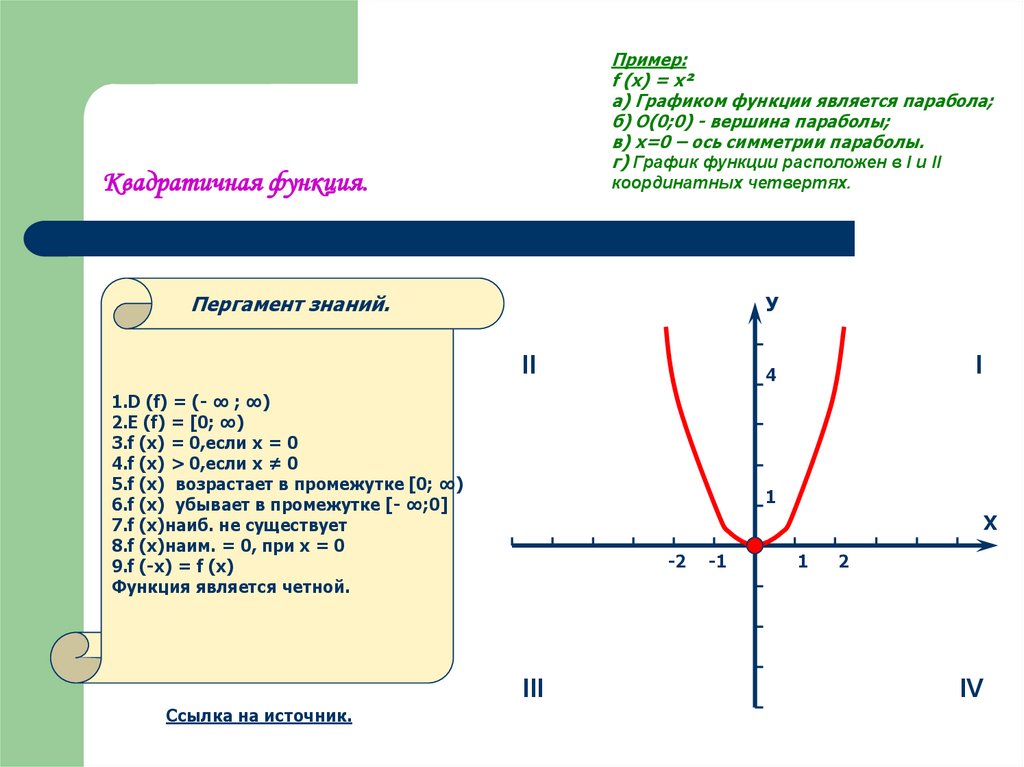
12. Квадратичная функция.
Пример:f (x) = х²
а) Графиком функции является парабола;
б) О(0;0) - вершина параболы;
в) х=0 – ось симметрии параболы.
г) График функции расположен в I и II
Квадратичная функция.
координатных четвертях.
Пергамент знаний.
У
II
1.D (f) = (- ∞ ; ∞)
2.E (f) = [0; ∞)
3.f (x) = 0,если х = 0
4.f (х) > 0,если х ≠ 0
5.f (x) возрастает в промежутке [0; ∞)
6.f (x) убывает в промежутке [- ∞;0]
7.f (x)наиб. не существует
8.f (x)наим. = 0, при х = 0
9.f (-x) = f (x)
Функция является четной.
1
Х
-2
III
Ссылка на источник.
I
4
-1
1
2
IV
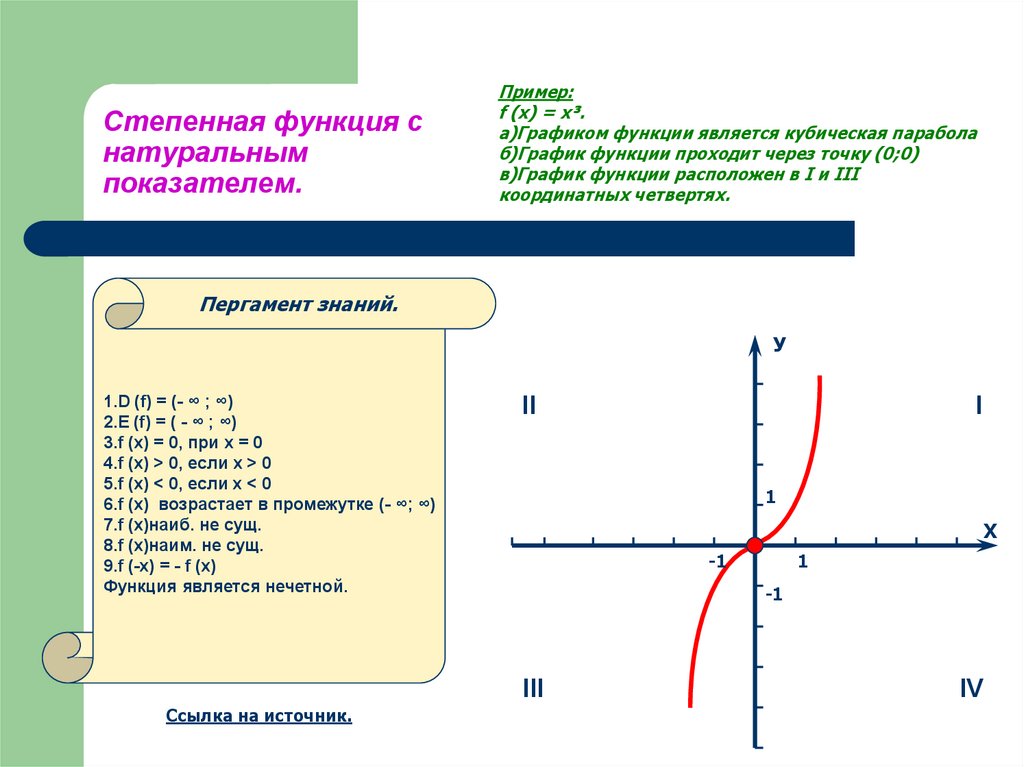
13. Степенная функция с натуральным показателем.
Пример:f (x) = x³.
а)Графиком функции является кубическая парабола
б)График функции проходит через точку (0;0)
в)График функции расположен в I и III
координатных четвертях.
Пергамент знаний.
У
1.D (f) = (- ∞ ; ∞)
2.E (f) = ( - ∞ ; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, если x > 0
5.f (x) < 0, если х < 0
6.f (x) возрастает в промежутке (- ∞; ∞)
7.f (х)наиб. не сущ.
8.f (х)наим. не сущ.
9.f (-x) = - f (x)
Функция является нечетной.
II
1
Х
-1
1
-1
III
Ссылка на источник.
I
IV
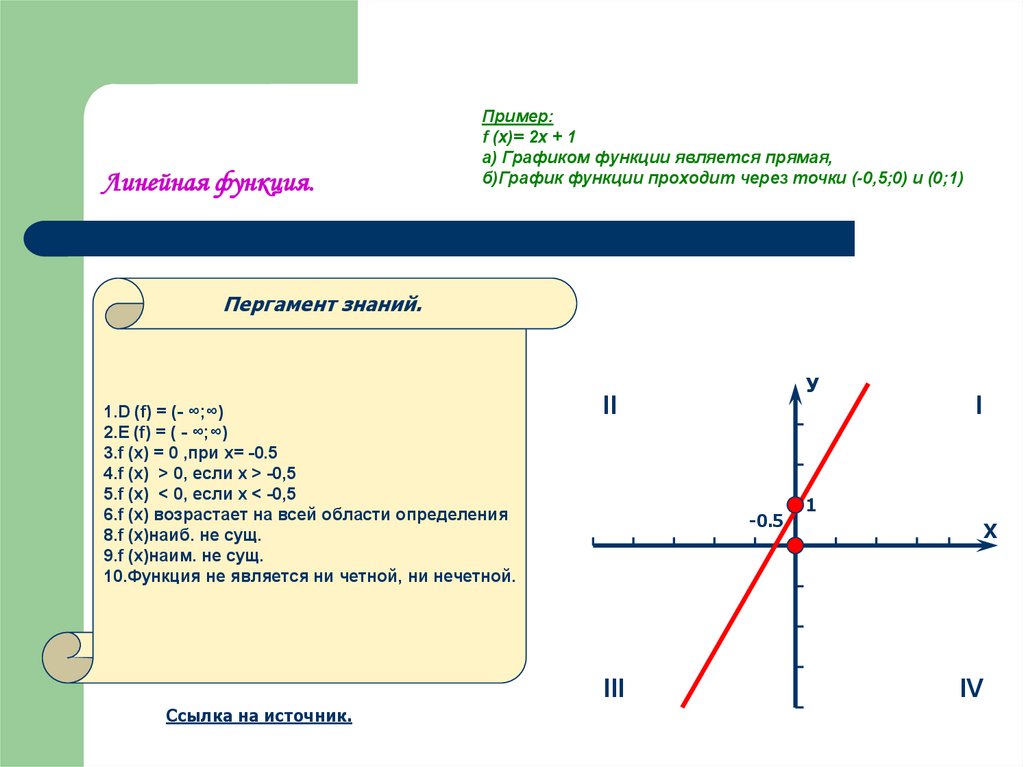
14. Линейная функция.
Пример:f (x)= 2x + 1
а) Графиком функции является прямая,
б)График функции проходит через точки (-0,5;0) и (0;1)
Пергамент знаний.
1.D (f) = (- ∞;∞)
2.E (f) = ( - ∞;∞)
3.f (x) = 0 ,при x= -0.5
4.f (x) > 0, если x > -0,5
5.f (x) < 0, если x < -0,5
6.f (x) возрастает на всей области определения
8.f (x)наиб. не сущ.
9.f (x)наим. не сущ.
10.Функция не является ни четной, ни нечетной.
-0.5
III
Ссылка на источник.
У
II
I
1
Х
IV
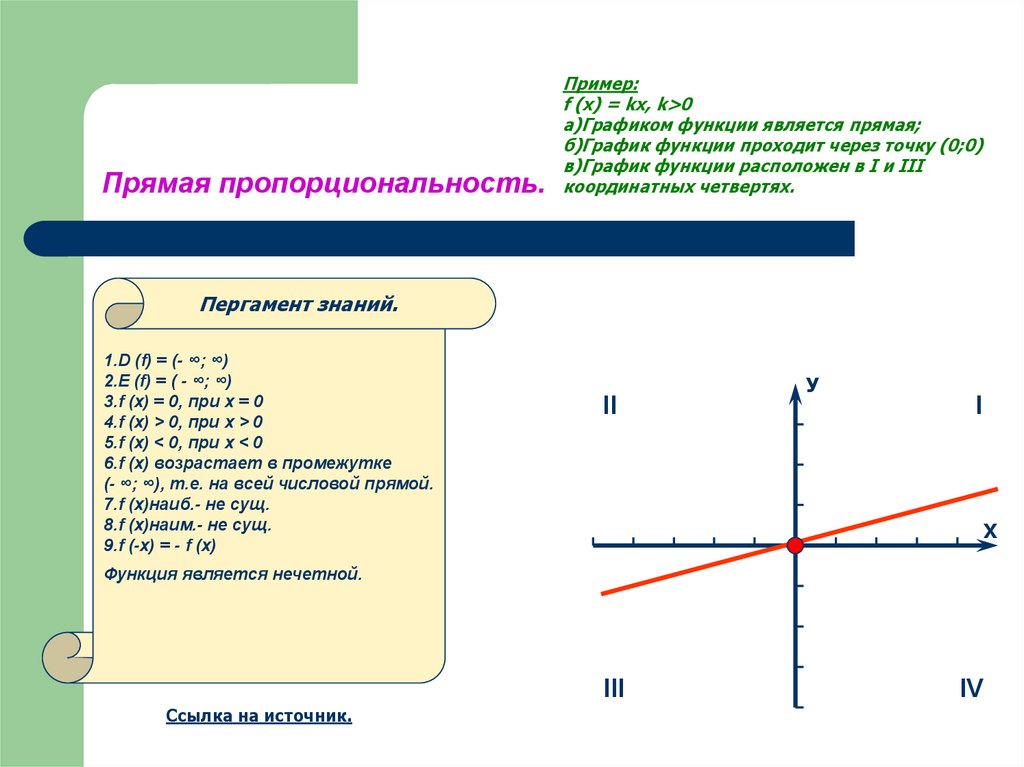
15. Прямая пропорциональность.
Пример:f (x) = kx, k>0
а)Графиком функции является прямая;
б)График функции проходит через точку (0;0)
в)График функции расположен в I и III
координатных четвертях.
Пергамент знаний.
1.D (f) = (- ∞; ∞)
2.Е (f) = ( - ∞; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, при x > 0
5.f (x) < 0, при x < 0
6.f (x) возрастает в промежутке
(- ∞; ∞), т.е. на всей числовой прямой.
7.f (x)наиб.- не сущ.
8.f (x)наим.- не сущ.
9.f (-x) = - f (x)
II
У
I
Х
Функция является нечетной.
III
Ссылка на источник.
IV
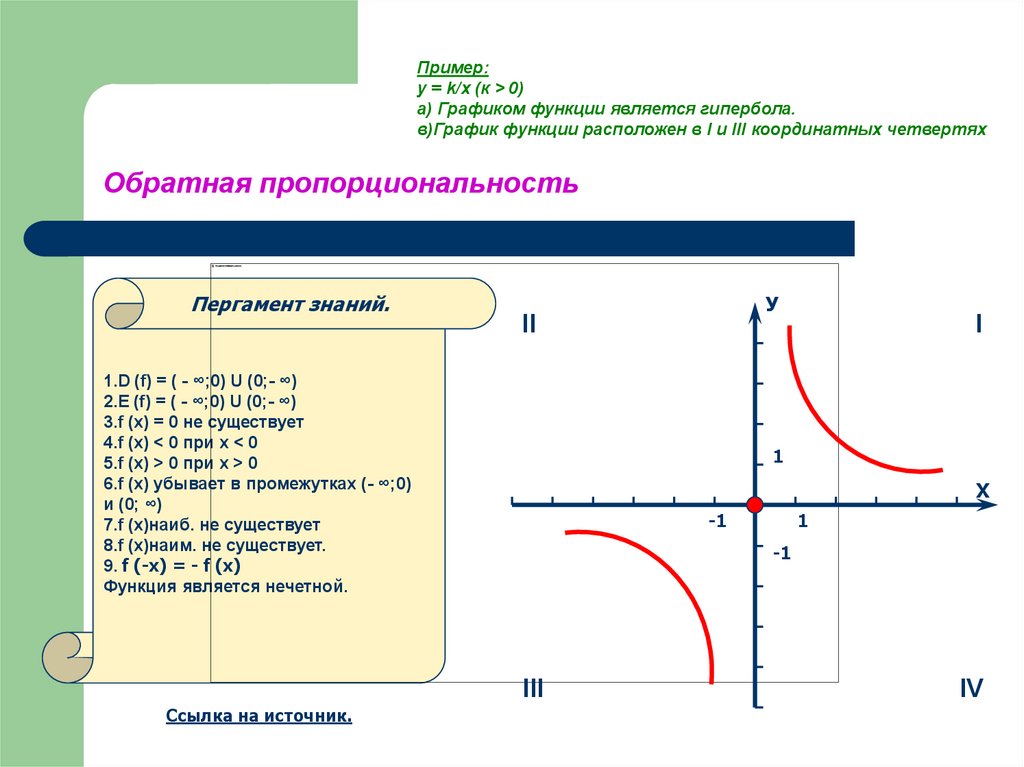
16. Обратная пропорциональность
Пример:y = k/x (к > 0)
а) Графиком функции является гипербола.
в)График функции расположен в I и III координатных четвертях
Обратная пропорциональность
Пергамент знаний.
II
1.D (f) = ( - ∞;0) U (0;- ∞)
2.E (f) = ( - ∞;0) U (0;- ∞)
3.f (x) = 0 не существует
4.f (x) < 0 при х < 0
5.f (x) > 0 при x > 0
6.f (x) убывает в промежутках (- ∞;0)
и (0; ∞)
7.f (x)наиб. не существует
8.f (x)наим. не существует.
9. f (-x) = - f (x)
Функция является нечетной.
I
1
Х
-1
1
-1
III
Ссылка на источник.
У
IV
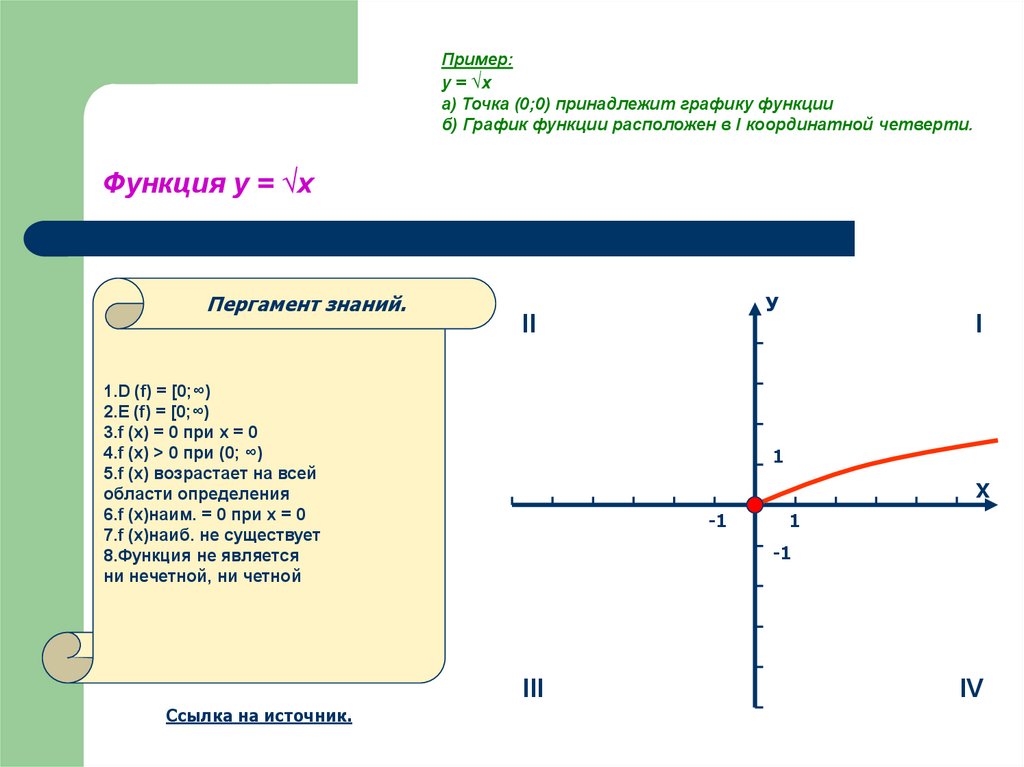
17. Функция у = √х
Пример:y = √x
а) Точка (0;0) принадлежит графику функции
б) График функции расположен в I координатной четверти.
Функция у = √х
Пергамент знаний.
II
1.D (f) = [0;∞)
2.E (f) = [0;∞)
3.f (x) = 0 при x = 0
4.f (x) > 0 при (0; ∞)
5.f (x) возрастает на всей
области определения
6.f (x)наим. = 0 при х = 0
7.f (x)наиб. не существует
8.Функция не является
ни нечетной, ни четной
I
1
Х
-1
1
-1
III
Ссылка на источник.
У
IV




 Математика
Математика








