Оптимизация параметров нечетких моделей методами роевого интеллекта

1.

Оптимизация параметров нечетких
моделей методами роевого интеллекта
И.А. Ходашинский,
профессор
кафедры автоматизации обработки
информации
Томского университета систем управления и
радиоэлектроники
[email protected]
Проведение научных исследований
Оптимизация параметров нечетких моделей
1

2.

Краткий обзор
1. Нечеткие системы
2. Алгоритм роящихся частиц
3. Алгоритм пчелиной колонии
4. Алгоритмы муравьиной колонии
- дискретный
- непрерывный
- прямой
5. Эксперимент
Проведение научных исследований
Оптимизация параметров нечетких моделей
2

3.

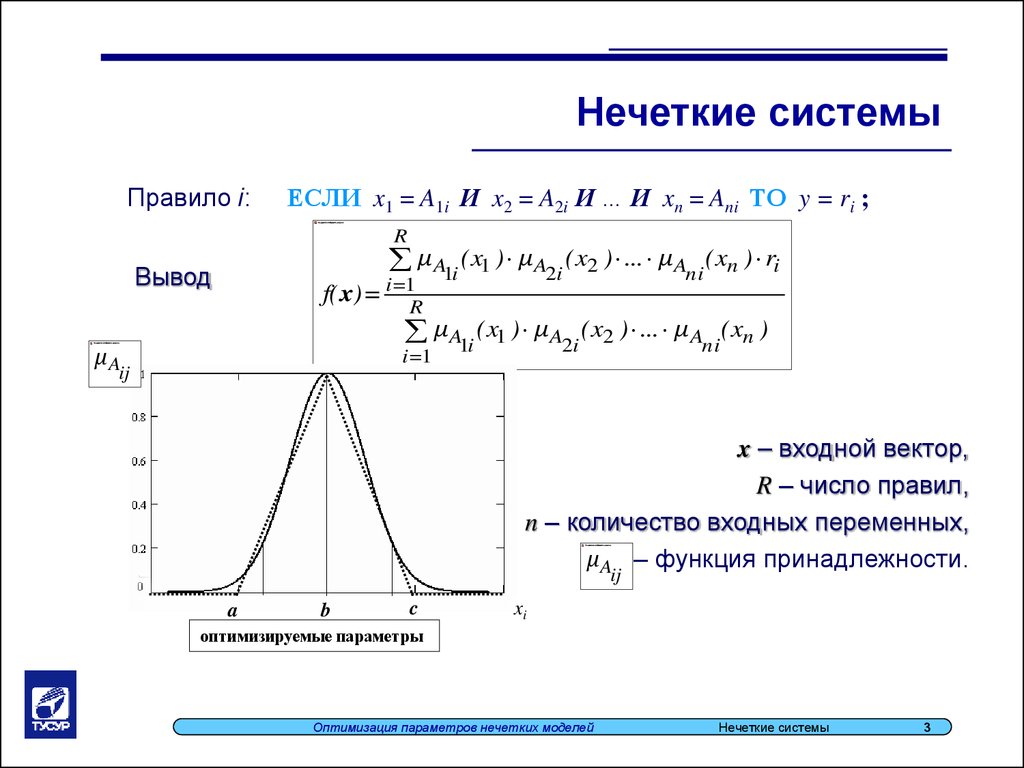
Нечеткие системы
Правило i:
ЕСЛИ x1 = A1i И x2 = A2i И … И xn = Ani ТО y = ri ;
R
μ A1i (x1 ) μ A2i (x2 ) ... μ Ani (xn ) ri
Вывод
f( x)= i=1
R
μ A1i (x1 ) μ A2i (x2 ) ... μ Ani (xn )
μA
i=1
ij
x – входной вектор,
R – число правил,
n – количество входных переменных,
μA – функция принадлежности.
ij
a
b
c
xi
оптимизируемые параметры
Оптимизация параметров нечетких моделей
Нечеткие системы
3

4.

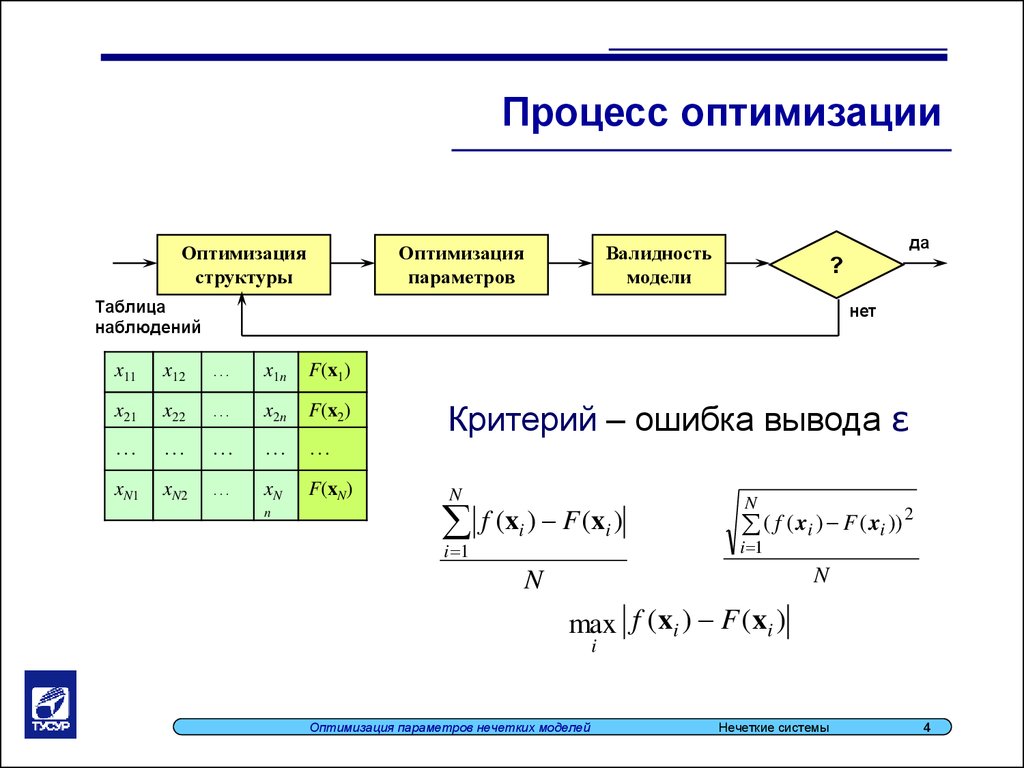
Процесс оптимизации
Оптимизация
структуры
Оптимизация
параметров
да
Валидность
модели
?
Таблица
наблюдений
нет
x11
x12
…
x1n
F(x1)
x21
x22
…
x2n
F(x2)
…
…
…
… …
xN1
xN2
…
xN
n
F(xN)
Критерий – ошибка вывода ε
N
i 1
f ( xi ) F ( x i )
N
( f ( xi ) F ( xi )) 2
i 1
N
N
max f (xi ) F (xi )
i
Оптимизация параметров нечетких моделей
Нечеткие системы
4

5.

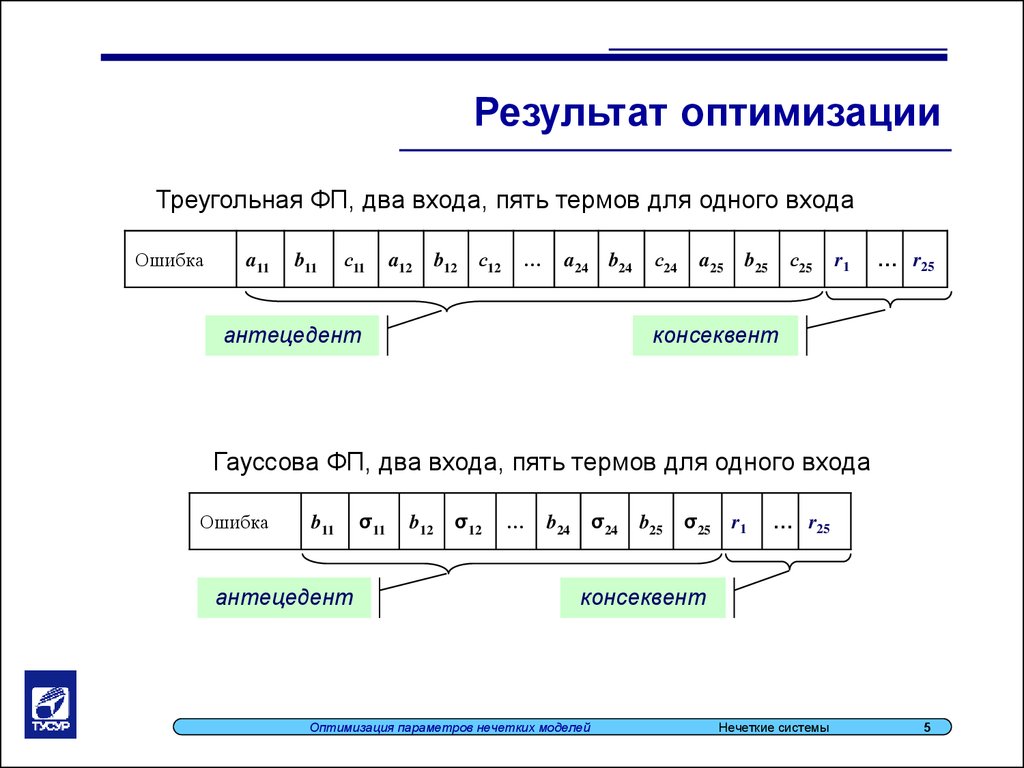
Результат оптимизации
Треугольная ФП, два входа, пять термов для одного входа
Ошибка
a11
b11
с11
a12
b12
с12
…
a24
b24
антецедент
с24
a25
с25
b25
r1
… r25
консеквент
Гауссова ФП, два входа, пять термов для одного входа
Ошибка
b11
антецедент
σ11
b12
σ12
…
σ24
b24
b25
σ25
r1
… r25
консеквент
Оптимизация параметров нечетких моделей
Нечеткие системы
5

6.

Рой, колония, стая
Децентрализация и самоорганизация,
простые правила взаимодействия
Nature,Vol 460,16, 2009
Оптимизация параметров нечетких моделей
Алгоритм роящихся частиц
6

7.

Концепция алгоритма роящихся частиц
xi ( xi1, xi 2 ,..., xin )
Координаты
определяют
параметры нечеткой системы.
Каждая частица оценивает свою позицию в
пространстве поиска.
Каждая частица помнит свою лучшую
позицию.
Каждая частица
позицию в
vi (viзнает
vin )
1, vi 2 ,...,лучшую
рое.
Скорость
динамически
корректируется.
Оптимизация параметров нечетких моделей
Алгоритм роящихся частиц
7

8.

Алгоритм роящихся частиц
xi (k 1) xi (k ) vi (k 1)
vi (k 1) w vi (k ) c1 rand ( pi (k ) xi (k )) c2 Rand ( pg (k ) xi (k ))
память
инерция
сотрудничество
s2
vi(k)
xi(k+1)
pi(k) – лучшая позиция i-ой частицы,
pg(k) – лучшая позиция частицы в рое,
c1 – когнитивный параметр,
c2 – социальный параметр
vi(k+1)
pg(k)
xi(k)
pi(k)
s1
Оптимизация параметров нечетких моделей
Алгоритм роящихся частиц
8

9.

Концепция алгоритма пчелиной колонии
Отсутствие иерархии и
централизованного управления
Обратная связь
Временная специализация: Разведчики
и Фуражиры
Распределение фуражиров в
зависимости от полезности ресурса
Оптимизация параметров нечетких моделей
Алгоритм пчелиной колонии
9

10.

Алгоритм пчелиной колонии
1. Задание начальных значений.
2. Для каждого разведчика формирование случайного
решения.
3. Определение лучшего решения.
4. Формирование массива фуражиров.
5. Формирование новых решений на базе фуражиров и
лучшего решения.
6. Вычисление нормированной ошибки новых и старых
решений.
7. Формирование массива разведчиков и фуражиров.
8. Если выполнено условие останова, то ВЫХОД,
иначе переход на шаг 2.
Оптимизация параметров нечетких моделей
Алгоритм пчелиной колонии
10

11.

Концепция алгоритма муравьиной колонии
Муравьи ищут самые короткие пути к
источнику пищи.
Каждый муравей считывает и оставляет
следы феромона на своем пути.
Следы феромона испаряются.
Распределение феромонов определяет
вероятность выбора в пространстве
решений.
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
11

12.

Дискретный АМК
4
3
С13 = 0.1
0.2
2
5
6
0.3
0.4
С12 = 0
7
0.5
1
0.6
1
8
12
0.9
11
0.8
0.7
9
10
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
12

13.

Дискретный АМК
1. Задать начальные параметры алгоритма и нечеткой системы.
2. Задать популяции муравьев в колониях.
3. Для всех муравьев текущей колонии определить дуги, для которых
вероятности выбора максимальны.
4. Передать в нечеткую систему значения параметров функций
принадлежности, определенных муравьями текущей колонии, и
вычислить ошибки. Если параметры, переданные муравьем в
нечеткую систему, лучше текущих, то сохранить новые значения
параметров.
5. Если имеется следующая колония, то сделать ее текущей и перейти
на шаг 3, иначе перейти на шаг 6.
6. Вычислить количество фермента на каждой дуге.
7. Вычислить количество испаренного фермента.
8. Если условие окончание работы алгоритма выполнено, то ВЫХОД,
иначе перейти к шагу 2.
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
13

14.

Дискретный АМК
ijk
Q
Lk (t )
ij (t 1) ( k ijk ij (t ))
ij (t 1) ij (t ) (1 )
количество феромона,
наносимого на дуги
увеличение количества
феромона
испарение феромона
где Q – количество феромона у муравья,
Lk(t) – значение ошибки,
Δτkij – количество нанесенного феромона,
ρ [0;1] – коэффициент снижения интенсивности феромона.
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
14

15.

Дискретный АМК
p(cij)
(i, j )
p(cij )
(
i
,
j
)
…
сi1 сi2 сi3 сi4 сi5
сiN-2 сiN-1сiN
где cij – это вес дуги (i;j) или нормированное значение параметра,
N – количество вершин,
α – эмпирический коэффициент, определяющий значимость фермента,
τ(i,j) – интенсивность фермента на дуге (i;j).
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
15

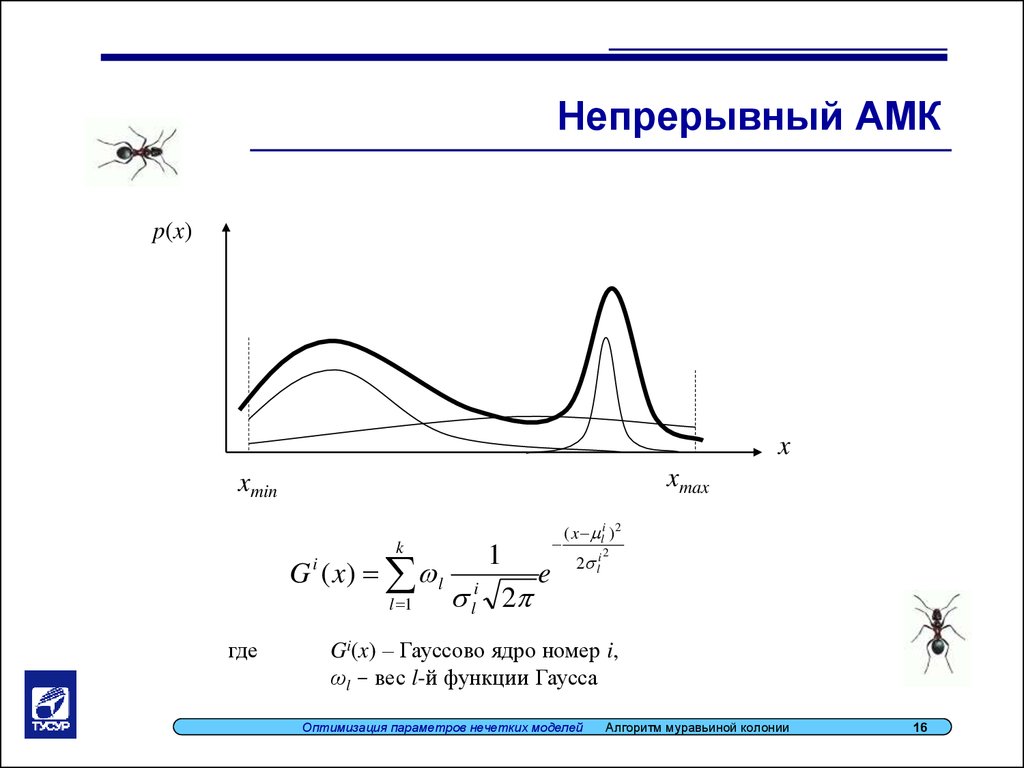
16.

Непрерывный АМК
p(x)
x
xmax
xmin
k
1
G ( x ) l i
e
l 2
l 1
i
где
( x li ) 2
2 li
2
Gi(x) – Гауссово ядро номер i,
ωl – вес l-й функции Гаусса
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
16

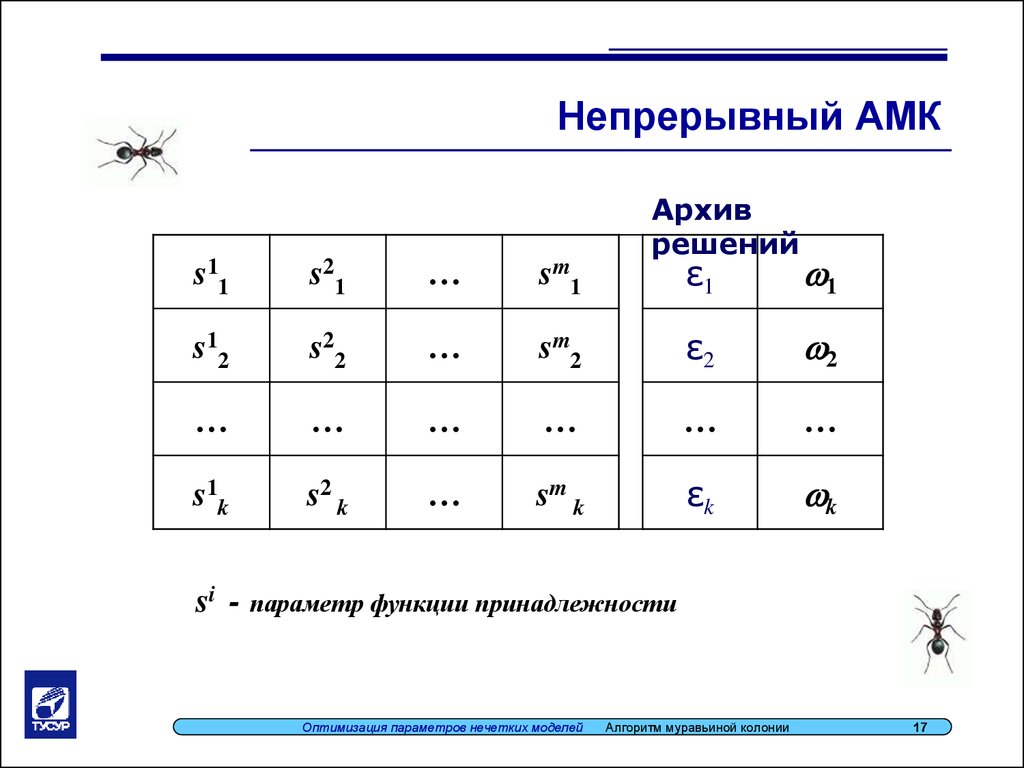
17.

Непрерывный АМК
Архив
решений
ε1
1
sm2
ε2
2
…
…
…
…
…
sm k
εk
k
s11
s2 1
…
sm1
s1 2
s2 2
…
…
…
s1 k
s2 k
si - параметр функции принадлежности
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
17

18.

l
1
e
qk 2
pl
( l 1) 2
2q 2k 2
l
вероятность выбора l-й функции Гаусса
k
вес l-го решения
Непрерывный
АМК
r
r 1
математическое ожидание функции
Гаусса
m s
i
l
i
l
k
i
l
e 1
s s
i
e
i
l
среднеквадратическое отклонение
функции Гаусса
k 1
где q – коэффициент сходимости алго
ξ – коэффициент скорости испарения фермента.
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
18

19.

Прямой АМК
bi ai
2
начальное значения параметра σ
μ(t) = (1– ρ) μ(t–1)
σ(t) = (1– ρ) σ(t–1)
увеличение количества фермента
μ(t) = μ(t) + ρθ(t)
σ(t) = σ(t) + ρ|θ(t) – μ(t)|
испарение фермента
i
dj = σj rand
cf
где
N
2 j
j 1
j
b
значение интервала локального поиска
aj
N
параметр конвергенции
μ, σ – параметры нормального распределения
ρ – эмпирический коэффициент испарения фермента
rand – равномерно распределенное число в интервале [0,1]
Оптимизация параметров нечетких моделей
Алгоритм муравьиной колонии
19

20.

Параметры АМК по умолчанию
F(x1, x2) = x1sin(x2)
Непрерывный
Количество итераций
50
Количество муравьев
10
Размер архива решений k
10
Коэффициент сходимости алгоритма q
0,1
Коэффициент скорости испарения ξ
Дискретный
Прямой
1
Коэффициент испарения ρ
0,4
Количество муравьев
20
α
1
Количество фермента - Q
0,1
Начальное количество феромона
10
Коэффициент испарения ρ
0,95
Шаг дискретизации
Оптимизация параметров нечетких моделей
15
Эксперимент
20

21.

Исследование размера архива решений
1
0,1
0,01
Î ø èáêà
ошибка
1E-3
1E-4
1E-5
1E-6
1E-7
1E-8
1E-9
1E-10
0
5
10
15
20
25
30
35
40
45
50
55
Ðàçì åðархива
àðõèâàрешения
ðåø åí èé
Размер
Оптимизация параметров нечетких моделей
Эксперимент
21

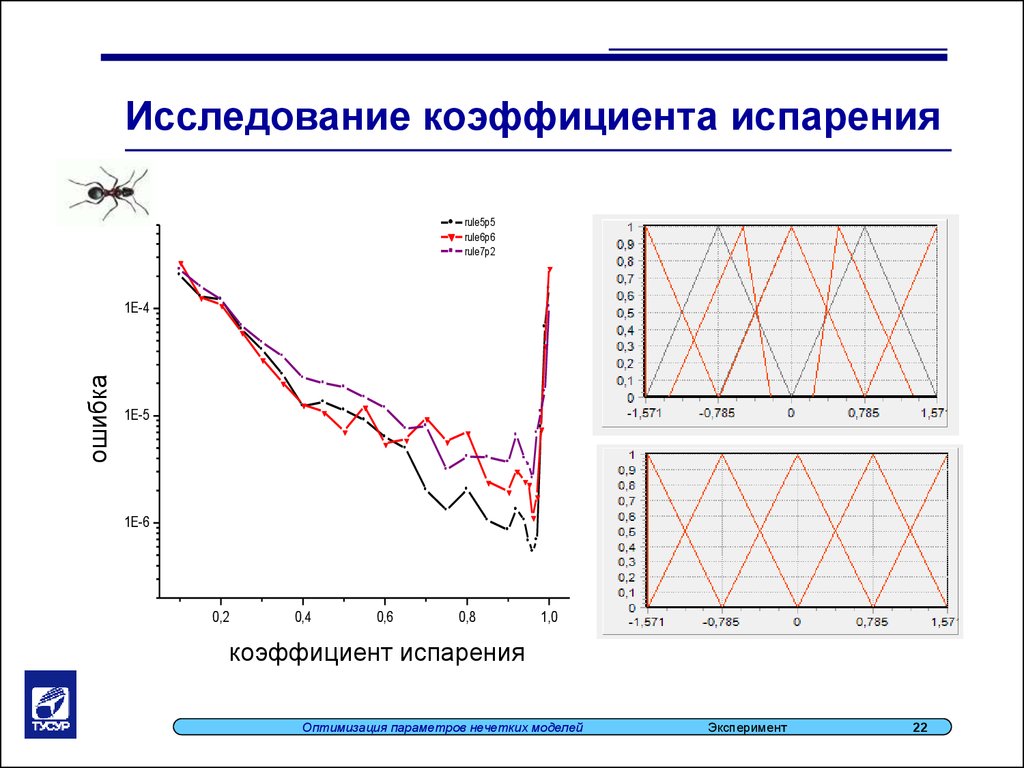
22.

Исследование коэффициента испарения
rule5p5
rule6p6
rule7p2
ошибка
Î ø èáêà
1E-4
1E-5
1E-6
0,2
0,4
0,6
0,8
1,0
ro
коэффициент
испарения
Оптимизация параметров нечетких моделей
Эксперимент
22

23.

Сравнительная динамика изменения ошибки
0,01
1E-3
1E-4
АМК прямой
АМК дискретный
АМК непрерывный
АПК
АРЧ
Ошибка
1E-5
1E-6
1E-7
1E-8
1E-9
1E-10
0
10
20
30
40
50
Время
Оптимизация параметров нечетких моделей
Эксперимент
23

24.

СПАСИБО
[email protected]
Проведение научных исследований
Оптимизация параметров нечетких моделей