Оптимизация методом нелинейного программирования (НЛП)

1.

1
ОПТИМИЗАЦИЯ
ХИМИКОТЕХНОЛОГИЧЕКИХ
ПРОЦЕССОВ
Модуль 3. Оптимизация методом нелинейного
программирования (НЛП)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

2. Представление химико-технологического процесса для построения математических моделей

x1
xr
Объект
y1
y f (x )
y
Объект = «черный ящик» или «black box» - эмпирическая
модель
Объект ≠ «черный ящик» или «black box» - физикохимическая модель
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
2

3.

Принципы построения теоретических
физико-химических моделей
3
Последовательные этапы
• Изучается теория процесса
• Составляется система уравнений математического
описания (МО)
• Выбирается алгоритм решения системы уравнений МО, т.н.
моделирующий алгоритм (МА)
• МА реализуется на компьютере и получается
математическая модель (ММ)
• Проверяется адекватность модели путем сравнения
расчетных результатов с экспериментальными
• В случае отсутствия адекватности модели решается задача
идентификации
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

4.

Идентификация математической модели
4
Идентификация – частный случай оптимизации, когда ищется
наименьшее значение критерия рассогласования
min y
РХТУ им. Д.И. Менделеева
расч
Кафедра информатики и компьютерного проектирования
y
эксп
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

5.

5
Структурная идентификация:
доп
Параметрическая идентификация:
a a
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
доп
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

6.

При построении теоретической физикохимической модели ХТП на основании
знания механизмов протекающих
процессов:
6
•Составляется система уравнений математического описания
(МО)
•Разрабатывается или выбирается алгоритм решения
системы уравнений математического описания, т.н.
моделирующий алгоритм (МА)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

7.

7
•Моделирующий алгоритм решения уравнений
математического описания реализуется на компьютере в виде
расчетного модуля технологического процесса в конкретном
аппарате
В результате получается математическая модель
ХТП, реализованная на компьютере, которая в случае ее
адекватности используется для исследования
реального производства.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

8.

Оптимизация процессов с использованием
математических моделей
Необходимо:
1) выбрать целевую функцию – критерий оптимальности R
R R( y
расч
)
Виды критериев оптимальности:
Технологические
Экономические
Технико-экономические
Термодинамические
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
8

9.

9
2) разработать и реализовать на компьютере адекватную
математическую модель
3) выбрать ресурсы оптимизации
- оптимизирующие или
управляющие параметры
4) Провести анализ параметрической чувствительности
критерия оптимальности (целевой функции) от ресурсов
оптимизации (оптимизирующих или управляющих
параметров)
5) Выбрать и реализовать алгоритм оптимизации
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

10.

Формулировка задачи оптимизации для
многих переменных
opt R u
u u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
доп
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
10

11.

11
Результат решения задачи оптимизации
u
opt
R
РХТУ им. Д.И. Менделеева
min
alg Opt
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

12.

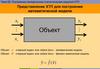
Решение задачи оптимизации для одной
переменной:
12
R
Поиск:
opt
u min u u max
R u
R min
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
min
Лекционный материал «Оптимизация ХТП»
u
V1.0 L3а
opt
u
max
u

13.

13
Графическое изображение оптимальных
значений оптимизирующих или управляющих
параметров в параметрической плоскости для
двух оптимизирующих переменных:
u2
u
max
2
u
u
opt
2
min
2
min
1
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
u1opt
u1max
Лекционный материал «Оптимизация ХТП»
u1
V1.0 L3а

14.

Результат решения задачи одномерной
оптимизации:
u
opt
R
РХТУ им. Д.И. Менделеева
min
alg Opt
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
14

15.

Формулировка задачи нелинейного
программирования (НЛП)
Ограничения Первого рода:
u
min
u u
max
Ограничения Второго рода:
x , u , a 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
15

16.

Формулировки задачи оптимизации при
использовании для её решения
математических моделей различных типов
В процессе проектирования новых и при эксплуатации
действующих ХТП ставятся и решаются схожие задачи
оптимизации.
В случае проектирования новых ХТП задача оптимизации
сводится к выбору оборудования, расчёту его
конструкционных и технологических параметров и синтезу
схемы обвязки оборудования материальными и тепловыми
потоками так, чтобы из имеющегося сырья произвести
заданное количество продуктов требуемого качества с
минимальными затратами и/или с максимальной прибылью.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
16

17.

17
При реконструкции или диверсификации ХТП задача
оптимизации подобна сформулированной выше с той лишь
разницей, что здесь дополнительно требуется, повозможности, сохранить существующую производственную
систему и с минимальными изменениями получить
улучшенную, соответствующую решению поставленных задач,
например, приносящую большую прибыль или другой,
расширенный ассортимент получаемых продуктов с
наименьшими затратами.
В отличие от задач оптимизации, задача оптимального
управления действующего ХТП состоит в выборе режимнотехнологических параметров ХТП для максимизации,
например, прибыли. Следует заметить, что прибыль, как
будет показано ниже, выступает в качестве одного из
основных экономических показателей, поскольку включает в
себя такие критерии, как выручка, капитальные и
эксплуатационные затраты, налоги, амортизация, кредит и т.п.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

18.

18
В общем случае для задач оптимизации ХТП используются
два типа математических моделей:
теоретические физико-химические
эмпирические статистические
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

19.

Математическая формулировка задачи
оптимизации
В дальнейшем будем полагать, что всегда ищется
экстремум, являющийся минимумом заданной целевой
функции многих переменных. Задача на поиск максимума
сводится к задаче на поиск минимума простым изменением
знака функции.
В результате задача оптимизации в узком смысле
(экстремальная задача) может быть записана как
x
РХТУ им. Д.И. Менделеева
min
R
(
x
)
min
max
x x
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
19

20.

20
min
max
В этом случае отрезок [ x , x
] представляет собой
ограничения 1-го рода, накладываемые на независимые
переменные, и соответствует области допустимых значений
независимых переменных оптимизации, в которой
определяются их оптимальные величины ( x opt ) ,
обеспечивающие минимум целевой функции:
R
РХТУ им. Д.И. Менделеева
min
R( x
Кафедра информатики и компьютерного проектирования
opt
Лекционный материал «Оптимизация ХТП»
)
V1.0 L3а

21.

21
Задача оптимизации в широком смысле (задача нелинейного
программирования) заключается в отыскании экстремума
целевой функции при заданных ограничениях в виде равенств
и (или) неравенств. Ограничения могут быть линейными и
(или) нелинейными.
Пусть непрерывная функция
целевую функцию;
1 ( x ), ..., m ( x )
R (x ) представляет собой
задают ограничения в виде равенств;
q m 1(x ), ..., q p (x ) – ограничения в виде неравенств.
Переменные x ( x1 , ..., xn ) могут быть конструкционными
параметрами, параметрами режимов, уставками регуляторов
и т.п.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

22.

22
Формально задача нелинейного программирования может
быть сформулирована следующим образом:
минимизировать
R( x ), x E
n
при линейных и (или) нелинейных ограничениях в виде
равенств
φ j ( x ) 0,
j 1, ..., m
и линейных и (или) нелинейных ограничениях в виде
неравенств
q j ( x ) 0,
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
j m 1, ..., p
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

23.

23
Решение этой задачи соответствует отысканию множества
1
n
x [ x , ..., x ]
удовлетворяющего двум последним соотношениям и
составляющего экстремум функции
R( x ), x E
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
n
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

24.

24
По аналогии с экстремальной задачей, задачу нелинейного
программирования можно представить следующим образом:
min R ( x )
x x x
φ j ( x ) 0 , j 1, ..., m
q j ( x ) 0, j m 1, ..., p
min
max
Здесь появляются ограничения 2-го рода в виде
предпоследних равенств и последних неравенств, что может
существенно усложнить решение задачи оптимизации.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

25.

Этапы решения задачи оптимизации
25
СТАРТ
Формулировка критерия оптимальности
Разработка (выбор) и реализация алгоритма математической модели ХТП
Выбор ресурсов оптимизации путём анализа параметрической
чувствительности математической модели ХТП
Формулировка ограничений I-го и II-го рода, накладываемых на параметры
ХТП
Выбор (разработка) и реализация алгоритма оптимизации для решения
задачи НЛП
СТОП
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

26.

26
Как следует из рисунка, для решения задачи оптимизации
необходимо:
сформировать (выбрать) критерий оптимальности
(целевую функцию);
найти ресурсы оптимизации – оптимизирующие
(управляющие) переменные;
определить ограничения I-го и II-го рода, накладываемые
на параметры процесса, исходя из физико-химических,
технологических, конструкционных и других соображений;
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

27.

27
выбрать (разработать) и реализовать два алгоритма:
а) алгоритм математической модели
б) алгоритм оптимизации;
реализовать процедуру анализа параметрической
чувствительности используемой адекватной ММ с целью
выявления взаимовлияния параметров процесса друг на
друга, определения чувствительности выбранного
критерия оптимальности (целевой функции) к изменению
физико-химических, режимных и конструкционных
параметров ХТП, а также для выбора оптимальных
ресурсов оптимизации – оптимизирующих (управляющих)
переменных, наиболее сильно влияющих на критерий
оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

28.

28
В общем случае критерий оптимальности должен
удовлетворять трём основным требованиям:
Во-первых, он должен быть количественным, то есть
выражаться числом, чтобы можно было количественно
сравнивать эффективность различных вариантов проведения
процесса.
Во-вторых, критерий оптимальности должен быть
единственным. Выполнение этого требования связано с
серьёзными затруднениями, так как на практике естественно
желание обеспечить оптимальные значения нескольких
критериев оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

29.

29
Например, для получения определённого целевого продукта
необходимо стремиться к тому, чтобы его концентрация на
выходе была максимальной, а себестоимость минимальной.
x, C
x
max
C
C
x
min
BCopt
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Bxopt
Лекционный материал «Оптимизация ХТП»
B
V1.0 L3а

30.

30
Из рисунка следует, что оптимальные значения ресурса
оптимизации будут различными для отличающихся друг от
друга критериев оптимальности - C и x.
Поэтому, если использовать один критерий, то получается
один результат ( B xopt и xmax).
Со вторым критерием – иной результат (
B xopt и Cmin).
В результате постановку задачи оптимизации с целью
определения расхода сырья , при котором себестоимость
станет минимальной а концентрация целевого продукта
максимальной, нельзя признать корректной. Неправильно,
например, искать оптимальные условия проведения
процесса, при которых выход продукта будет максимальным,
а концентрация примеси в нём минимальной. Иногда эти
требования несовместимы.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

31.

31
В настоящее время всё большее распространение получает
так называемые обобщённые критерии оптимальности,
которые являются некоторой функцией рассмотренных
частных критериев оптимальности. В этом случае
обобщённый критерий представляется в виде суммы
(аддитивный критерий) или в виде произведения
(мультипликативный критерий) частных критериев. При этом
весовые коэффициенты позволяют правильно определить
степень вклада всех частных критериев в обобщённый
критерий оптимальности. В результате при оптимизации
ведётся поиск экстремального значения единственного, но
обобщенного критерия оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

32.

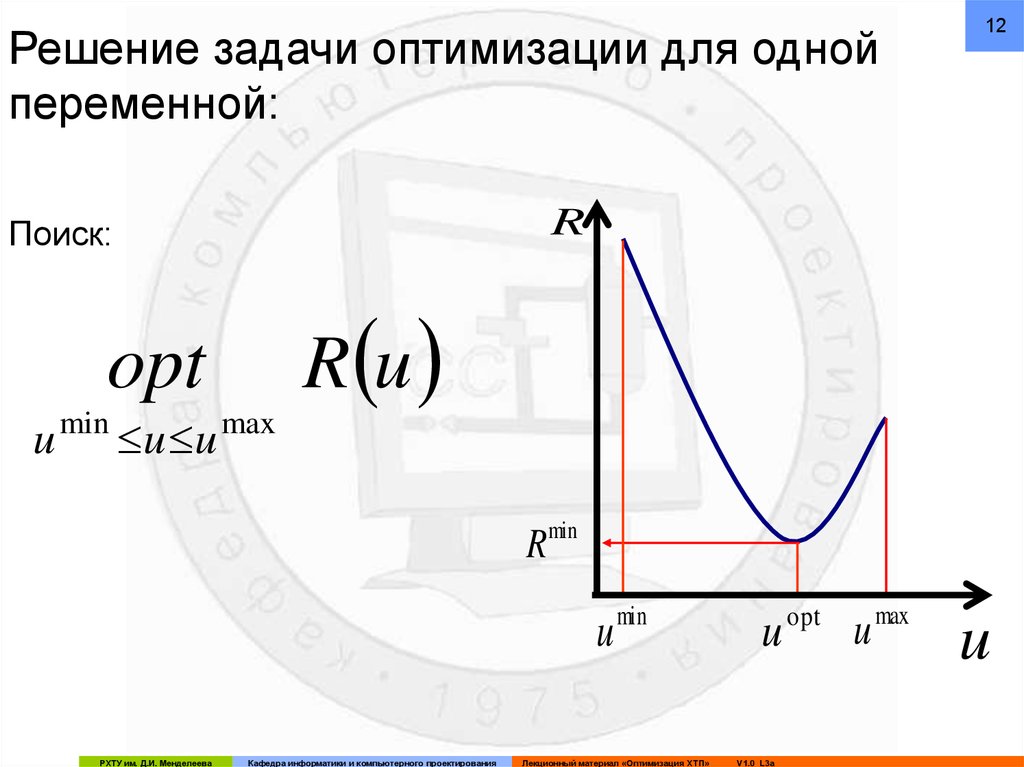
32
Третье требование к критерию оптимальности:
монотонное изменение его величины в зависимости от
оптимизирующих переменных. При незначительных
изменениях критерия оптимальности в зависимости от
оптимизирующих переменных возникают большие
затруднения при определении их оптимальных значений.
R
R max
R max
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
opt
u
opt
Лекционный материал «Оптимизация ХТП»
u
V1.0 L3а

33.

33
Как видно из рисунка, оптимальные условия, которые могут
быть определены при этом – uopt*, Rmax*, существенно
отличаются от действительных оптимальных условий - uopt,
Rmax, (велико Δu = uopt* - uopt). В этом случае критерий
оптимальности нечувствителен к изменению
оптимизирующих переменных.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

34.

34
Когда экстремум критерия оптимальности имеет ярко
выраженный характер, также необходимы эффективные
методы оптимизации, которые позволяют найти оптимальные
условия - uopt, Rmax.
R
R max
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
u
opt
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

35.

35
В этом случае значительное отклонение от оптимальных
условий uopt может привести к существенному изменению
показателя качества функционирования ХТП – критерия Rmax.
Поэтому поддержание оптимальных условий в реальном
процессе становится сложной задачей из-за большой
чувствительности экстремального значения критерия
оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

36.

36
Наличие нескольких экстремумов и точек разрыва функции
критерия оптимальности усложняет процедуру оптимизации
R
R
B
max
A
C D
R
E
min
F
u min
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
u
u max
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

37.

37
В этом случае необходимо найти либо наибольшее значение
функции (точка B), либо наименьшее значение (точка F), то есть
глобальный экстремум. Если в процессе оптимизации будет
определён локальный экстремум (точка A) - локальный
максимум или точка C на отрезке [A, B] - локальный минимум,
точка E - локальный минимум), то это приведёт к неверным
координатам оптимальных условий. Определённые сложности
могут возникнуть при расчёте глобального максимума (точка B)
из-за разрыва функции критерия оптимальности в этой точке.
Таким образом, необходимым условием успешного решения
задачи является исследование характера изменения функции
критерия оптимальности. Так как процесс формулировки
критерия оптимальности не формализован и в известной
степени носит субъективный характер, необходимо
стремиться к тому, чтобы функция критерия была
унимодальной с одним экстремумом и не содержала точек
разрыва.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

38.

I. Прямые методы поиска экстремума
функции одной переменной
38
Прямые методы в качестве критерия движения к экстремуму
используют сравнительную оценку величины целевой
функции, вычисленной в соответствующих точках. Следует
отметить, что прямые методы поиска экстремума функции
одной переменной имеют не только самостоятельное
значение, но и широко используются как вспомогательные
методы при поиске экстремума функции многих переменных.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

39.

I.1. Интервальные методы
Метод сканирования
39
R
h
xmin
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
xmax x
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

40.

40
Интервал поиска [xmin, xmax] разбивается на n равных участков,
длина каждого из которых равна шагу поиска h. Далее
последовательно определяется значение целевой функции
R(x) во всех точках разбиения и в точках xmin и xmax , и
запоминается наименьшее значение. Таким образом,
экстремум может быть найден с точностью до шага поиска.
Основным достоинством метода является его простота и
возможность нахождения глобального экстремума.
Недостатком метода является большой объем вычислений,
которые необходимо выполнять при его реализации.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

41.

Метод локализации экстремума
41
Метод локализации представляет собой модификацию
метода сканирования. При его использовании существенно
снижается количество выполняемых вычислений целевой
функции.
R
xmin 1 x1 2 x2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
x3
Лекционный материал «Оптимизация ХТП»
xmax x
V1.0 L3а

42.

42
Весь интервал поиска [xmin, xmax], как и в методе сканирования,
разбивается на несколько частей (подынтервалов) точками x1,
x2 и x3, но более крупных размеров.
Вычисляется значение критерия R(x) во всех точках разбиения
и в точках xmin, xmax.
Все значения R(x) сравниваются между собой и из них
выбирается наименьшее, если ищем минимум, и наибольшее,
если ищем максимум. Далее выбирается новый интервал
поиска, равный двум подынтервалам, с наименьшим
(наибольшим) вычисленным значением R на их общей
границе (на рисунке это соответствует интервалу [xmin, x2].
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

43.

43
Этот интервал меньше исходного и в нем локализован
экстремум. Затем поступают следующим образом. Интервал,
в котором локализован экстремум, делят на несколько
подынтервалов (на рисунке точками 1 и 2) и снова вычисляют
значения критерия оптимальности в точках деления.
Сравнивают их между собой, находят наименьшее,
локализуют экстремум в меньшем интервале (на рисунке в
интервале 1–2) и т.д. до тех пор, пока экстремум не будет
локализован в интервале, размер которого соответствует
заданной точности поиска.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

44.

44
Наилучшие результаты поиска получаются в том случае, когда
первоначальный интервал [xmin, xmax] разбивается на четыре
равных поди нтервала (n = 4). При этом каждый последующий
подинтервал делится пополам и вычислять значение функции
нужно только в двух новых точках, так как ее значения на
концах нового интервала и в его середине известны из
предыдущих расчетов.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

45.

45
Абсолютная ошибка в нахождении экстремума в этом случае
определяется выражением:
( xmax xmin ) 2
s 1
2
s – количество точек, в которых вычисляется значение
критерия оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

46.

46
Так, при s = 21, относительная ошибка составит:
10
2 0,001
xmax xmin
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

47.

Метод золотого сечения
47
В основе этого метода лежит правило геометрического
отношения или золотого сечения:
a b
b c
a
или
ac b
c
b
2
a – длина всего отрезка; b – длина его большей части; c –
длина его меньшей части.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

48.

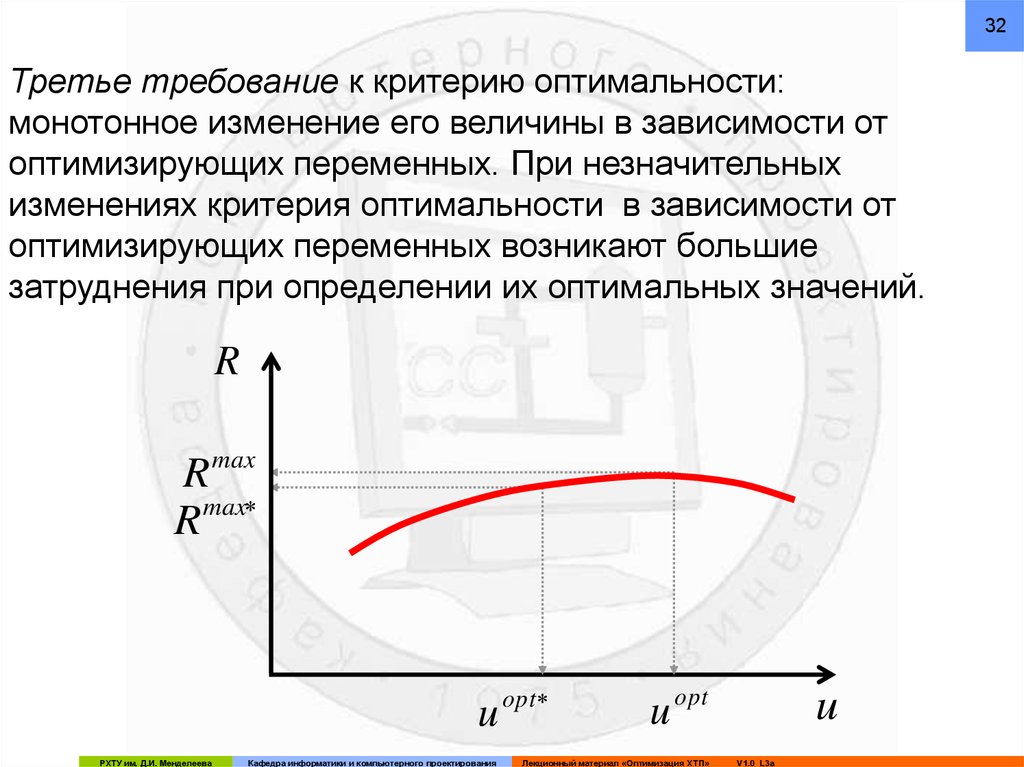
48
В соответствии с этим законом определяются точки
исследуемого интервала, в которых необходимо производить
вычисление целевой функции R.
R
xmin x4 x3 x1 x2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
xmax x
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

49.

49
Из рисунка следует, что:
c a b
Тогда :
a ( a b) b
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
2
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

50.

50
Обозначив отношение b/a = k и подставив его в последнее
выражение, получим:
a k a k a 0
2
2
2
2
откуда следует:
k k 1 0
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

51.

51
Решение последнего уравнения дает:
1 1 4 1 5
k
2
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

52.

52
Поскольку k > 1, его значение принимается равным:
1 5
k
0.62
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

53.

53
Порядок поиска экстремума методом золотого сечения
следующий.
На исследуемом интервале [xmin, xmax] определяются две точки:
x1 xmin k a
x
x
k
a
min
2
2
a – длина интервала [xmin, xmax]
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

54.

54
В точках x1 и x2 рассчитываются значения целевой функции R.
По найденным значениям R(x1) и R(x2) определяется
подынтервал, в котором локализован экстремум. Этот
подынтервал состоит из двух подынтервалов не равной
длины.
На рисунке минимальное значение будет R(x1) в точке x1.
Подынтервал, в котором локализован экстремум, будет [xmin,
x2]. Далее внутри большего подынтервала (в нашем примере
внутри [xmin, x1]) находится точка, отстоящая от общего конца
интервала на расстоянии k2b, где b – длина подынтервала, в
котором локализован экстремум [xmin, x2], причем b = k · a .
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

55.

55
В нашем примере это будет
x3 xmin k (k a)
2
xmin k a
3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

56.

56
Нетрудно видеть, что величина интервала [x1, x2] также равна
k3a. В самом деле, величина [xmin, x2] равна ka, 1 – k = k2, тогда
величина (x1 - x2) будет определяться:
ka k a ka(1 k ) k a
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
3
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

57.

57
Таким образом, (x2 - x1) = (x3 - xmin), следовательно,
рассчитывать длину интервала [xmin, x3] нет необходимости.
Далее вычисляется R(x3) и сравниваются значения R(x2), R(x1) и
R(x3). Находится минимальное (в примере R(x3)), и процедура
продолжается до достижения требуемой точности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

58.

58
Абсолютная ошибка в определении экстремума после s
вычислений будет:
xmax xmin
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
5 1
2
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
s 3

59.

59
Для s = 21 относительная ошибка есть:
1
18
0,62
xmax xmin 2
0,9 10
4
точность расчета значительно превосходит точность расчета
по методу локализации при одном и том же количестве
вычислений.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

60.

I.2. Шаговые методы
Метод с обратным переменным шагом
60
В методе при произвольно заданном шаге h от левой границы
интервала поиска выполняется движение с расчетом
значения функции на каждом шаге до тех пор, пока шаги
удачные, т.е. функция уменьшается. В случае неудачного шага
выполняется движение в обратном направлении с
уменьшенным шагом поиска, пока шаги удачные. Если шаг
оказывается снова неудачным, его опять уменьшают.
Минимум будет достигнут, когда шаг поиска станет меньше
предварительно заданной точности по аргументу.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

61.

Графическая интерпретация метода с
обратным переменным шагом
61
R
0
1
2
5
6
xmin
РХТУ им. Д.И. Менделеева
3
4
xopt
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
xmax
V1.0 L3а
x

62.

Метод поиска с использованием чисел
Фибоначчи
62
Последовательность чисел Фибоначчи, определяемая
реккурентным соотношением:
Fn Fn 1 Fn 2 ; F0 F1 1
может быть использована для организации поиска
экстремума функции одной переменной.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

63.

63
Абсолютная погрешность, возникающая при поиске этим
методом, не превышает величины:
xmax xmin
FS
Fs - s-е число в последовательности чисел Фибоначчи.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

64.

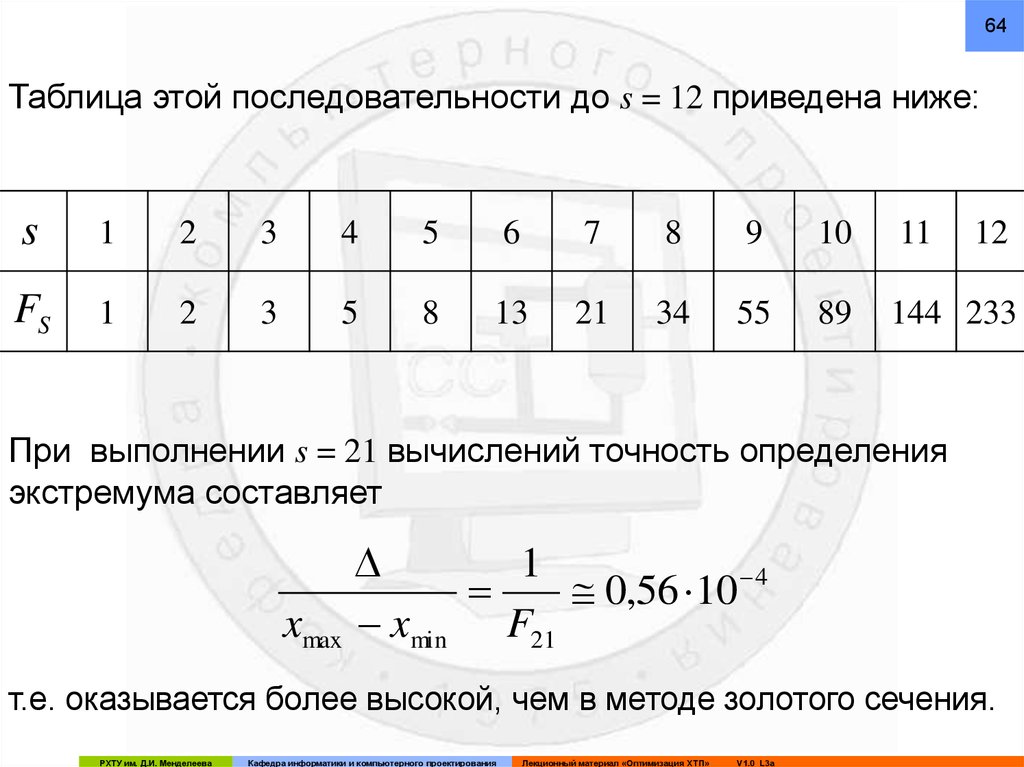
64
Таблица этой последовательности до s = 12 приведена ниже:
s
1
2
3
4
5
6
7
8
9
10
11
FS
1
2
3
5
8
13
21
34
55
89
144 233
12
При выполнении s = 21 вычислений точность определения
экстремума составляет
1
4
0,56 10
xmax xmin F21
т.е. оказывается более высокой, чем в методе золотого сечения.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

65.

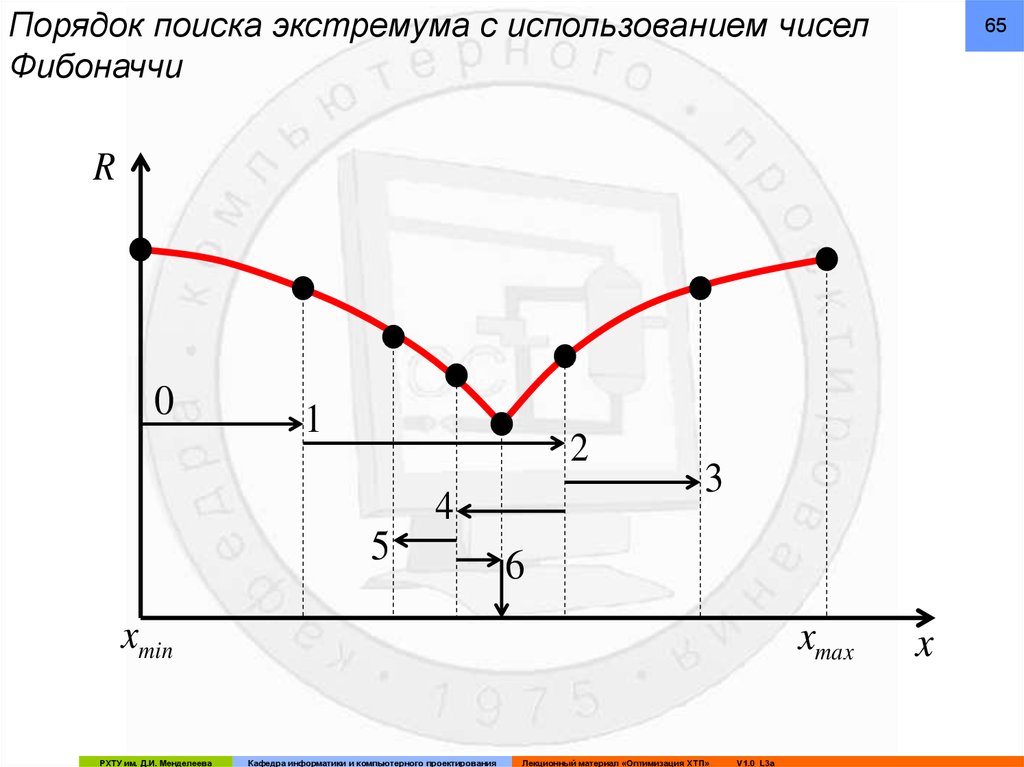
Порядок поиска экстремума с использованием чисел
Фибоначчи
65
R
0
1
2
4
5
3
6
xmin
РХТУ им. Д.И. Менделеева
xmax
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
x

66.

66
1. По заданной точности ∆ поиска рассчитывается
вспомогательное число:
xmax xmin
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

67.

67
2. Находится число Фибоначчи Fs, такое, что:
FS 1 N FS
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

68.

68
3. Определяется минимальный шаг поиска:
hmin
РХТУ им. Д.И. Менделеева
xmax xmin
FS
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

69.

69
4. Рассчитывается значение R в точке, определяемой
соотношением:
x1 xmin hmin FS 2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

70.

70
5. Рассчитывается значение R в точке, определяемой
соотношением:
x2 x1 hmin FS 3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

71.

71
6. Если шаг оказался удачным, т.е.:
R( x2 ) R( x1 )
то рассчитывается значение R в точке, определяемой
соотношением:
x3 x2 hmin FS 4
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

72.

72
6. Если шаг оказался неудачным, т.е.:
R( x2 ) R( x1 )
то x3 определяется:
x3 x1 hmin FS 4
Процедура продолжается последовательно до тех пор, пока
не будут исчерпаны все числа Фибоначчи в убывающей
последовательности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

73.

Условия окончания поиска экстремума
функции одной переменной
73
• Точность по аргументу
xi 1 xi 10
7
• Точность по функции
f ( xi 1 ) f ( xi ) 10
8
i – номер итерации или
число расчетов
функции
• Число расчетов значений целевой функции:
Число расчетов 10000
Лучше эти три условия использовать одновременно
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

74.

Пример 1
74
Найти глобальный минимум функции
f ( x) x 0.5 x 28 x 140
4
3
2
В пакете MatLab для определения глобального минимума в
интервале -6; 6 используется функция fminbnd, которая
записывается
[ xopt , Rmin ] fminbnd(' f ( x) ' , 6,6)
xopt 3.9339
Rmin 84.2624
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

75.

75
II.1. Прямые методы поиска
экстремума функции многих
переменных, не использующие
производные (методы нулевого
порядка)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

76.

Метод сканирования
76
Исследуется целевая функция вдоль одного выбранного
направления (вдоль одной из координатных осей) с шагом h1.
В каждой точке вычисляется и запоминается значение
целевой функции. После того как весь диапазон изменения
этой переменной исследован и для него найдено
минимальное (максимальное) значений целевой функции,
изменяется значение другой переменной на величину шага h2
и опять исследуется диапазон первой переменной, в котором
снова определяется искомый экстремум, и т.д. После
нахождения всех экстремумов находится искомый глобальный
экстремум.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

77.

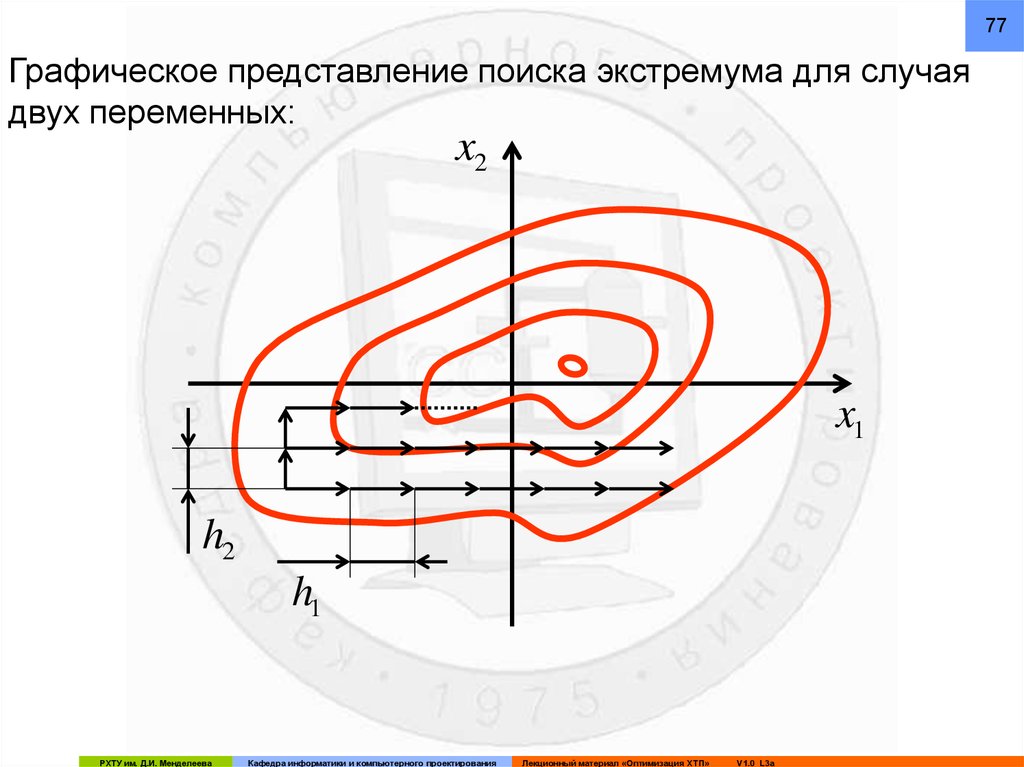
77
Графическое представление поиска экстремума для случая
двух переменных:
x2
x1
h2
h1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

78.

78
Для произвольного числа переменных шаг по каждой
следующей переменной производится после того, как
завершен цикл по предыдущей.
Если имеются ограничения, то точки, которые не
удовлетворяют уравнениям (или неравенствам) ограничений
исключаются, и в них не вычисляются значения критерия R.
Однако каждую точку требуется проверять относительно
ограничения. Если переменных много, то такого рода
проверка также требует длительного времени.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

79.

79
Прием проверки ограничений типа равенств может быть
представлен в виде:
x j f ( x1 , x 2 , ..., x j 1 , x j 1 , ..., x n )
при этом поиск ведется по n-1 переменной, а значение xj
рассчитывается из этого соотношения. Разумеется, что xj
должно проверяться на допустимый диапазон его изменения.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

80.

80
Если относительная точность поиска равна e по каждой из
переменных, то количество вычислений целевой функции,
необходимых для поиска экстремума, составит
1
S
n
n – число переменных
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

81.

81
Метод сканирования имеет существенный недостаток,
связанный с тем, что число вычислений при определении
положения оптимума очень велико и возрастает в
показательной степени от размерности решаемой задачи.
Преимущество метода – простота, возможность определения
глобального экстремума. Метод может быть использован для
грубого анализа областей расположения экстремумов.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

82.

Метод поочередного изменения
переменных (метод Гаусса–Зейделя)
x2
x1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
82

83.

83
Движение к оптимуму происходит по каждой из осей до
частного экстремума. Они чередуются. Первая ось, по
которой осуществляется поиск минимума (максимума),
выбирается произвольно. Частный экстремум (по одной
переменной) может быть найден любым из методов поиска
экстремума функции одной переменной.
После того как найден частный минимум (максимум) по
первой оси, начинается поиск минимума (максимума) по
второй оси при условии, что значение первой переменной
равно найденному минимуму (максимуму) на первой оси.
Далее определяется минимум (максимум) на второй оси и, с
учётом изложенного, осуществляется поиск по третьей,
четвертой и т.д. оси. Процесс последовательно продолжается
до тех пор, пока не будет достигнута заданная точность
локализации экстремума, т.е. если шаг по каждой из осей
приводит к возрастанию функции, а величина шага меньше
или равна заданной точности поиска, то расчет закончен.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

84.

Метод пробных движений
84
Дается приращение по всем переменным
xi
j 1
xi xi
j
j 1
i – номер переменной, j – номер шага
и вычисляются значения целевой функции.
Из всех опробованных направлений выбирается то, в котором
уменьшение (увеличение) целевой функции наибольшее. В
j 1
этом направлении делается рабочий шаг h, больший xi
и находится новая точка, из которой делаются пробные
движения. Процедура повторяется до достижения заданной
точности поиска.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

85.

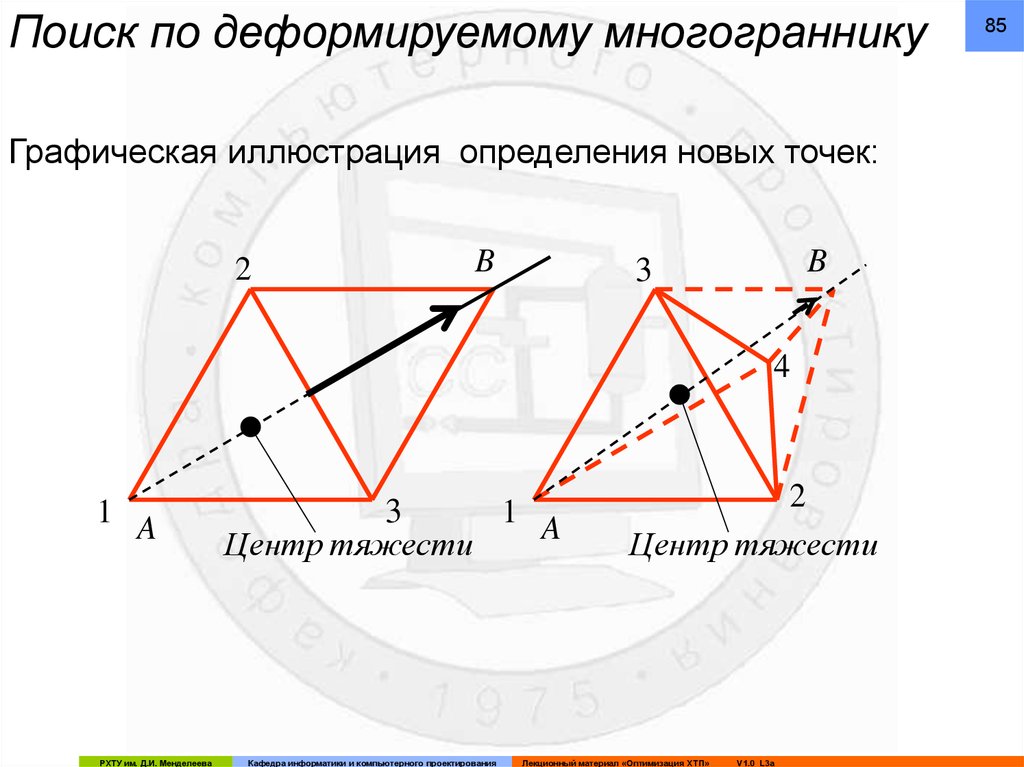
Поиск по деформируемому многограннику
Графическая иллюстрация определения новых точек:
2
B
B
3
4
1 A
РХТУ им. Д.И. Менделеева
3
1 A
Центр тяжести
Кафедра информатики и компьютерного проектирования
2
Центр тяжести
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
85

86.

86
Поиск по деформируемому многограннику (метод Нелдера и
Мида) основан на использовании нерегулярных
многогранников (деформируемых симплексов). Для случая
двух переменных регулярный симплекс – равносторонний
треугольник (три точки); в случае трех переменных – тетраэдр
(четыре точки) и т.д.
При поиске минимума целевая функция может быть
вычислена в каждой из вершин симплекса: из вершины, где
целевая функция максимальна (точка A) проводится
проектирующая прямая через центр тяжести симплекса.
Затем точка исключается и строится новый симплекс,
называемый отраженным из оставшихся прежних точек и
одной новой точки B, расположенной на проектирующей
прямой на задаваемом расстоянии от центра тяжести.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

87.

87
Наличие оврагов и хребтов целевой функции приводит к
необходимости изменять размеры и форму симплекса в
процессе поиска.
В методе Нелдера и Мида минимизируется функция n
независимых переменных с использованием n + 1 вершин
деформируемого многогранника. Каждая величина
идентифицируется вектором x . Вершина, в которой
значение R (x ) максимально, проектируется через центр
тяжести оставшихся вершин. Улучшенные значения целевой
функции находятся последовательной заменой точки с
максимальным значением R (x ) на более «хорошие» точки,
пока не будет найден минимум R (x )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

88.

Алгоритм метода Нелдера–Мида
k
k
k
k
88
Пусть xi [ xi1 , ..., xij , ..., xin ] , i = 1, …, n + 1,является i –
й вершиной (точкой в n – мерном пространстве En на k – м
этапе поиска k = 0, 1, …, и пусть значение целевой функции в
точке x i(k )равно R ( xi(k ) ) . Кроме того, отметим те векторы x
многогранника, которые дают максимальное и минимальное
значения R (x ) .
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Τ
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

89.

89
Определим
R( x
где
(k )
h
) max{ R( x
(k )
1
), ..., R( x
(k )
n 1
)}
), ..., R( x
(k )
n 1
)}
1 h n 1
и
R( x
где
(k )
) min{ R( x
(k )
1
1 n 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

90.

90
Пусть
x
(k )
n 2
– центр тяжести всех вершин, исключая
x
(k )
h
Тогда координаты этого центра тяжести определятся
формулой:
x
(k )
n 2, j
1
(k )
(k )
xij xhj
n i 1
n 1
j 1, ..., n
j – координатное направление
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

91.

91
Начальный многогранник обычно выбирается в виде
регулярного симплекса с точкой 1 в качестве начала
координат. Процедура отыскания min R ( x ) состоит из
следующих 4 операций:
(k )
x
1. Отражение – проектирование
через центр тяжести в
h
соответствии с соотношением
x
(k )
n 3
x
(k )
n 2
α( x
(k )
n 2
x
α > 0 – коэффициент отражения
x n( k )2 – центр тяжести
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
(k )
h
)

92.

92
(k )
(k )
R
(
x
)
R
(
x
2. Растяжение. Если
n 3
) , то вектор
( x n( k 3) x n( k )2 ) растягивается в соответствии с соотношением
x
(k )
n 4
x
(k )
n 2
γ( x
(k )
n 3
x
(k )
n 2
)
γ > 1 – коэффициент растяжения
Если R( x n 4 ) R( x ) , то x h заменяется на x n 4 и
процедура продолжается снова с операции 1 при k = k + 1.
(k )
(k )
(k )
(k )
В противном случае x h(k ) заменяется на x n( k 3) и также
осуществляется переход к операции 1 при k = k + 1.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

93.

93
(k )
(k )
R
(
x
)
R
(
x
) для всех i ≠ h, то вектор
3. Сжатие. Если
n 3
i
( xh( k ) xh( k )2 ) сжимается в соответствии с формулой:
x
(k )
n 3
x
(k )
n 2
β(x
(k )
h
x
(k )
n 2
0 < β < 1 – коэффициент сжатия
(k )
Затем x h
заменяется на
операции 1.
РХТУ им. Д.И. Менделеева
x n( k 3) и происходит возврат к
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
)

94.

94
(k )
(k )
R
(
x
)
R
(
x
4. Редукция. Если
n 3
h ), все векторы
( xi( k ) ) ( x ( k ) ) , i = 1, …, n+1, уменьшаются в два раза с
(k )
отсчетом от x по формуле:
(k )
i
x
x
(k )
0,5( x
(k )
i
x
i 1, ..., n 1
Затем осуществляется переход к операции 1.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
(k )
)

95.

95
Критерий окончания поиска, использованный Нелдером и
Мидом, имеет следующий вид:
1/ 2
1
(k )
(k ) 2
R( xi ) R( xn 2 )
n 1 i 1
n 1
ε
где ε – произвольное малое число
Деформируемый многогранник адаптируется к топографии
целевой функции, вытягиваясь вдоль длинных наклонных
плоскостей, изменяя направление в изогнутых впадинах и
сжимаясь в окрестности минимума.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

96.

Методы случайного поиска
96
В основе методов случайного поиска лежит стратегия
нахождения экстремума функции путем перебора
совокупностей случайных значений независимых
переменных. Эти методы, получившие общее название
методов Монте-Карло, успешно применяются с
использованием вычислительных машин для решения задач
обращения матриц, нахождения собственных значений и
собственных векторов матриц, решения систем
алгебраических уравнений и целого ряда других задач.
Общим для всех методов случайного поиска является
генерирование и использование случайных чисел в процессе
поиска, отличием – стратегия движения к экстремуму.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

97.

97
Из методов случайного поиска наибольшее распространение
получил метод случайного направления. При использовании
этого метода очередное приближение определяется
соотношением:
( k 1)
i
x
x
(k )
i
h β
(k )
i 1, 2, ..., n
h(k) – параметр шага
βi – компонент случайного вектора
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
β
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
(k )
i

98.

98
( k 1)
) в новой точке оказывается
Если значение функции f ( x
меньше предыдущего f ( x (k ) ) , то в качестве очередного
приближения принимаются последние значения неизвестных
( k 1), в противном случае остаются предыдущие значения x (k )
x
Процедура генерирования случайного направления (вектора
β (k ) ) повторяется до тех пор, пока не будет найден экстремум
функции.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

99.

99
Известно несколько модифицированных методов случайного
поиска. Так, например, метод случайных направлений с
обратным шагом рекомендует при неудачном шаге делать
сразу же шаг в обратном направлении, равном h ( k ) β ( k ),
что позволяет существенно сократить время поиска. Если и
обратный шаг окажется неудачным, то можно из предыдущей
точки сделать новый шаг, сгенерировав новый случайный
вектор направления, или перейти к поиску с меньшим
значением шага.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

100.

II.2. Прямые методы поиска экстремума
функции многих переменных,
использующие производные (методы
первого порядка)
100
Методы оптимизации с использованием производных, как
правило, более эффективны в смысле скорости сходимости,
чем методы, не использующие производные. Однако,
приближённый расчёт производных численными методами
трудоёмок и трудно оценить погрешность полученных при
этом результатов.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

101.

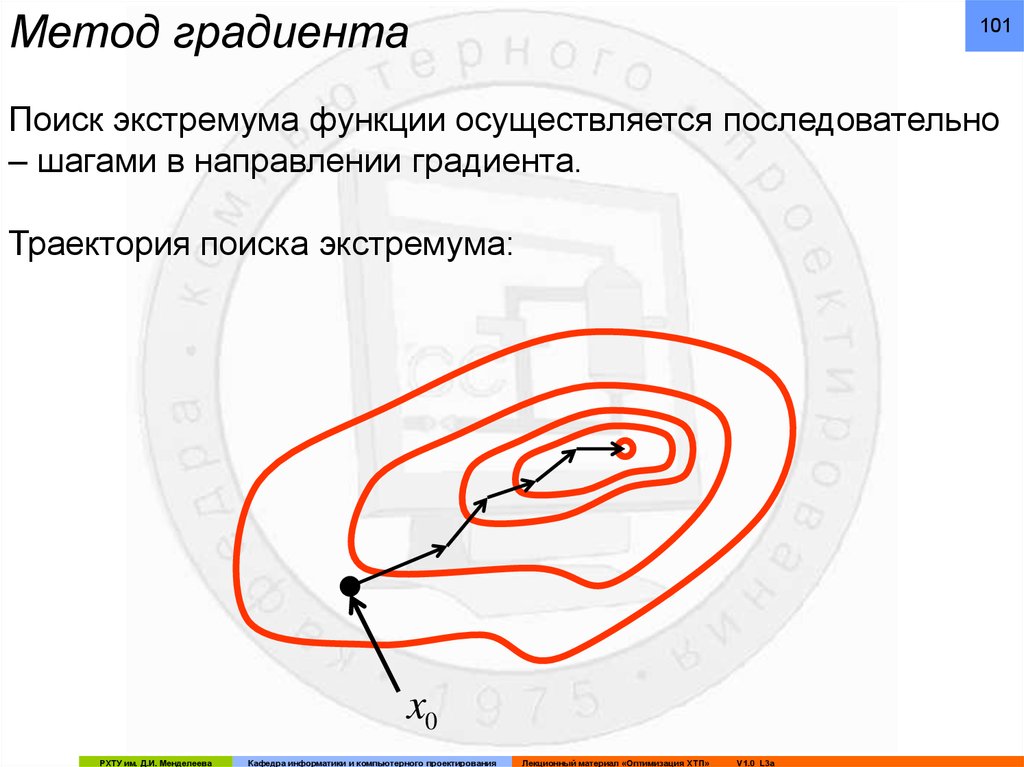
Метод градиента
101
Поиск экстремума функции осуществляется последовательно
– шагами в направлении градиента.
Траектория поиска экстремума:
x0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

102.

102
Алгоритм поиска имеет вид:
xi
j 1
R
xi h
xi
j
j
i 1,...n
i – номер переменной
j – номер шага поиска
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

103.

103
В начальной точке поиска x ( x1 , x2 , ..., xn ) вычисляется
градиент функции, а затем находятся координаты положения
точки x 1 ( x11 , x12 , ..., x1n )
0
0
0
0
R 0
1
0
x1 x1 h x x ;
1
R 0
1
0
x ;
x2 x2 h
x 2
...............................
R 0
1
0
x
x
h
x
.
n
n
x n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

104.

104
1
1
1
1
x
(
x
,
x
,
...,
x
В полученной точке
1
2
n ) снова вычисляется
градиент функции и находится точка x 2 ( x12 , x22 , ..., xn2 )
R 1
2
1
;
x
h
x
x
1
1
x1
R 1
2
1
x ;
x2 x2 h
x 2
...............................
R 1
2
1
x n x n h x x .
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

105.

105
Величина h носит название фактора шага. Процесс
продолжается до тех пор, пока экстремум не будет найден с
достаточной точностью, т.е. пока не будут выполнены
неравенства:
1
1
R( x
,x
1
2
, ..., x
1
i
x
1
n
) R( x , x , ..., x )
1
2
x εi
i
i 1,...n
ε – заданная точность поиска
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
n

106.

Метод наискорейшего спуска
(крутого восхождения)
106
Метод наискорейшего спуска напоминает собой метод
градиента, т.е. в исходной точке определяется направление
наискорейшего возрастания функции (градиент). Затем вдоль
этого направления делается не один шаг, как в методе
градиента, а продолжается движение до нахождения
максимума вдоль этого направления. Затем в точке
максимума вновь определяют градиент и осуществляется
движение в направлении этого градиента до частного
максимума и т.д. до тех пор, пока не находится абсолютный
максимум функции цели
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

107.

107
Путь поиска экстремума методом наискорейшего спуска
x0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

108.

108
Направление, противоположное нормированному
(единичному) градиенту R (x ) , т.е. направление
(k )
наискорейшего спуска, определяется в точке x
E
E
(k )
(k )
R( x
(k )
)
R( x
(k )
)
– единичный вектор в направлении градиента
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
k
R( x )

109.

109
(k )
На k-м этапе переход из точки x в точку
описывается следующим соотношением:
x
( k 1)
x
x
РХТУ им. Д.И. Менделеева
x
(k )
(k )
(k )
x
λ E
λ
(k )
( k )
Кафедра информатики и компьютерного проектирования
x
( k 1)
(k )
(k )
R( x )
Лекционный материал «Оптимизация ХТП»
(k )
V1.0 L3а

110.

110
Подстановка в последнее выражение предыдущего дает
следующее соотношение для метода наискорейшего спуска:
x
( k 1)
РХТУ им. Д.И. Менделеева
x
λ R( x )
(k )
R( x )
(k )
(k )
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
(k )
V1.0 L3а

111.

111
Поскольку выражение
λ
(k )
R( x )
(k )
– скалярная величина, то оно может быть заменено
некоторым числом λ*(k)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

112.

112
Тогда
x
( k 1)
x
(k )
λ
( k )
R( x )
(k )
Поиск в соответствии с этим выражением осуществляется
многократно.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

113.

113
Для каждого направления градиента осуществляется
минимизация функции R( x k )
Это может осуществляться формально путем вычисления λ из
уравнения:
dR( x
РХТУ им. Д.И. Менделеева
(k )
k
λ E
dλ
Кафедра информатики и компьютерного проектирования
(k )
Лекционный материал «Оптимизация ХТП»
)
V1.0 L3а
0

114.

114
Но чаще используют тот или иной метод одномерного поиска
для определения величины λ*(k), минимизирующей на k-м
шаге поиска целевую функцию.
Метод наискорейшего спуска позволяет найти экстремум при
минимальном объеме вычислений. Метод особенно выгодно
использовать в том случае, когда градиент функции
изменяется не резко. Очевидно, что вблизи экстремума метод
наискорейшего спуска вырождается в метод градиента. В
качестве критерия окончания поиска можно использовать те
же критерии, что и в методе градиента.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

115.

Метод релаксаций
115
Метод также использует производные, в частности, – первые
производные целевой функции и состоит в нахождении
осевого направления, вдоль которого целевая функция
возрастает наиболее быстро.
Для этого в начальной точке поиска определяются
производные функции по всем переменным R xi
По той оси, вдоль которой производная наибольшая, и
производится движение до частного минимума одномерным
методом поиска. Затем анализ производных вновь
повторяется. Критерием окончания поиска может служить
следующее положение: если при движении из очередной
точки не наблюдается дальнейшее возрастание целевой
функции, то максимум найден.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

116.

116
Алгоритм поиска при методе релаксаций имеет вид:
xi
j 1
РХТУ им. Д.И. Менделеева
R
j
j
xi h sign
x
i
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

117.

117
j
x i – значение переменной, по которой происходит
оптимизация на данном шаге
1, если y 0;
sign y 0, если y 0;
1, если y 0,
hj – фактор шага, величина которого изменяется в процессе
поиска
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

118.

118
Обычно шаг выбирается так: вначале он принимается равным
числу h1 = δ, затем делается еще один шаг в этом направлении
h2 = h1, если шаг оказался успешным, то он удваивается h3 =
2h2.
Если же следующий шаг оказался не успешным, то из
предыдущей точки, в которой был удачный шаг, делаются
шаги в 2 раза меньше, чем последний удачный. Уменьшение
величины шага в области максимума производится до
заданного значения, определяемого желаемой точностью.
Метод релаксаций можно рассматривать как комбинацию
методов, использующих производные.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

119.

Условия окончания поиска экстремума
функции одной переменной
119
• Точность по аргументу
xi 1 xi 10
7
• Точность по функции
f ( xi 1 ) f ( xi ) 10
8
i – номер итерации или
число расчетов
функции
• Число расчетов значений целевой функции:
Число расчетов 10000
Лучше эти три условия использовать одновременно
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

120.

Пример 2
120
Найти минимум функции
x1 x2 10
f ( x) ( x1 x2 )
3
2
2
В пакете MatLab для определения минимума с начальными
приближениями: 15, 25 используется функция fminsearch,
которая записывается
[ xopt , Rmin ] fminsearch(' f ( x) ' , [15, 25])
xopt [5, 5]
Rmin 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

121.

II.3. Численные методы оптимизации при
наличии ограничений 2-го рода
121
Все методы оптимизации при наличии ограничений делятся
на два класса: методы сведения к задаче безусловного
экстремума без ограничений и методы прямого решения
задач с ограничениями.
Среди методов, сводящих задачу с ограничениями к
безусловной оптимизации, наиболее широко распространены
методы штрафных функций.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

122.

Методы штрафных функций
122
При решении задач оптимизации химико-технологической
системы существует, как правило, ряд ограничений типа
равенств (например, значения потоков в местах разрывов в
схемах с обратной связью), так и ограничения типа
неравенств (например, технологические ограничения по
диапазону концентраций, температур, давления и т.д.).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

123.

Тогда в общем виде задачу можно сформулировать
следующим образом:
минимизировать
R( x ), x
min
x x
max
при ограничениях
φi ( x ) 0, i 1, ..., m
g i ( x ) 0, i m 1, ..., p
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
123

124.

124
В основу методов штрафных функций положена идея
преобразования общей нелинейной задачи в
последовательность задач без ограничений путем добавления
к целевой функции одной или нескольких функций, задающих
ограничения с тем, чтобы ограничения, как таковые, в задаче
оптимизации не фигурировали.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

125.

125
Например, необходимо минимизировать функцию
R ( x) ax b
Где ОГРАНИЧЕНИЯ II-го РОДА
имеют вид:
x0 x x1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

126.

126
Графическая иллюстрация целевой функции при поиске
оптимума без использования метода штрафных функций
R (x )
x0
x1
x
Ясно, что ограничение x1 должно сдерживать любой шаговый
метод поиска, такое ограничение называется активным.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

127.

127
Одним из наиболее простых методов штрафа является
изменение целевой функции с тем, чтобы образовать
локальный экстремум в окрестности активного ограничения.
С этой целью формируется новая целевая функция
(штрафная функция):
P( x) ax b ( x x1 )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
2

128.

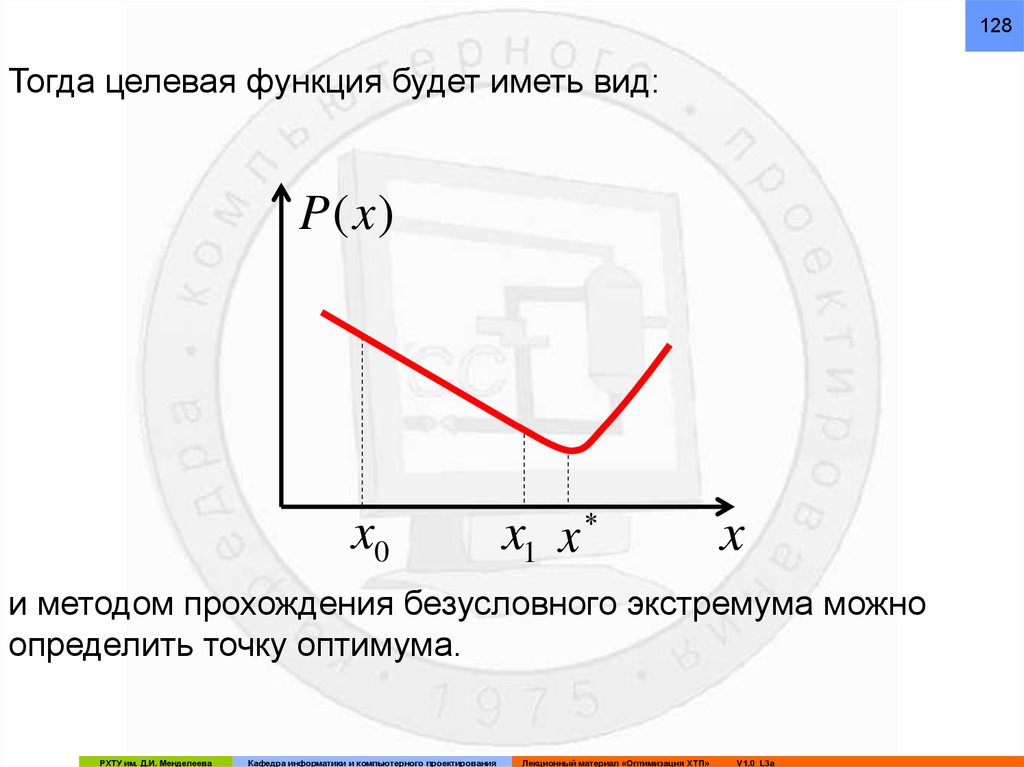
128
Тогда целевая функция будет иметь вид:
P (x )
x0
x1 x
x
и методом прохождения безусловного экстремума можно
определить точку оптимума.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

129.

129
Однако, получается точка, отстоящая от границы и,
следовательно, от точного решения на величину (x1 – x*), что
не всегда удовлетворяет точности решения задачи.
Для того, чтобы удовлетворить точности, необходимо ввести
некоторый множитель μ, который называется весовым
коэффициентом (μ > 1).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

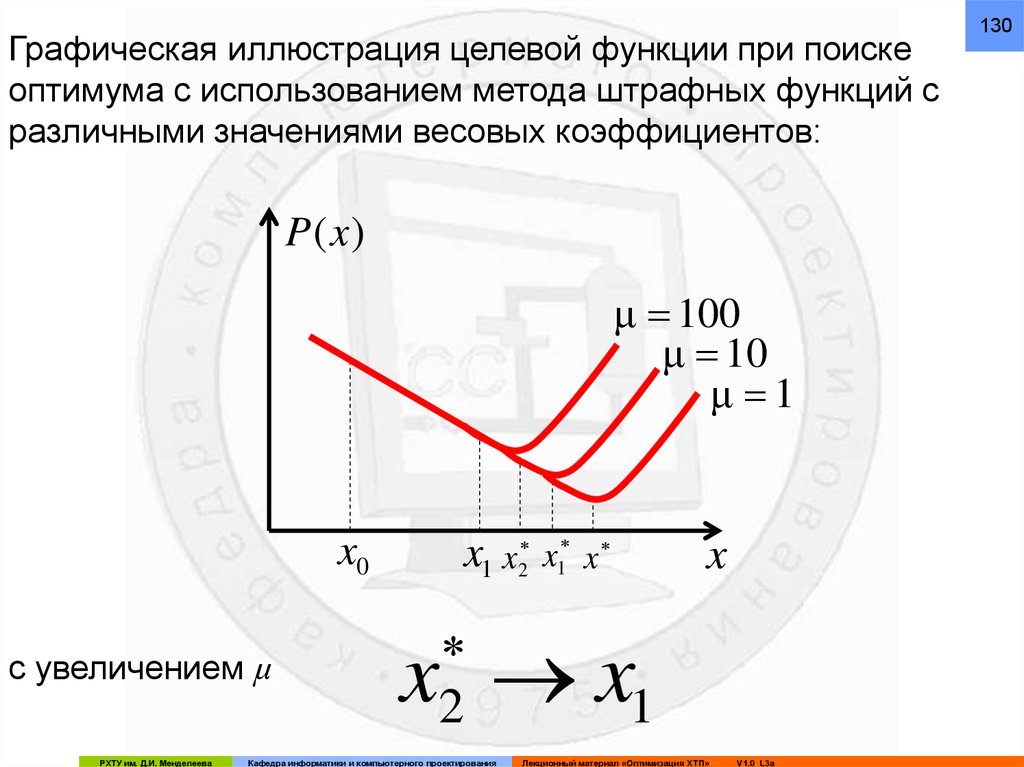
130.

Графическая иллюстрация целевой функции при поиске
оптимума с использованием метода штрафных функций с
различными значениями весовых коэффициентов:
P (x )
μ 100
μ 10
μ 1
x0
с увеличением μ
РХТУ им. Д.И. Менделеева
x1 x2
x1 x
x
2
x x1
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а
130

131.

131
Аналогично можно ввести штрафную функцию для
ограничений в виде равенств, тогда обобщенный критерий
оптимизации примет вид:
m
P( x ) R( x ) μ i φ ( x )
2
i
i 1
p
u
g
(
x
)
i
i m 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
2
i
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

132.

132
μi – весовые коэффициенты
u – оператор Хевисайда, который принимает значения 0 и 1,
если в точке x k
g i ( xk ) 0
и 1, если
gi ( xk ) 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

133.

133
Таким образом, вводя, штрафную функцию мы тем самым
выделяем своеобразную «стену» на границе области и чем
больше μi, тем она «круче». Однако на этой же границе
образуется овраг, который резко замедляет скорость
сходимости любого метода, а для некоторых он непроходим.
Поэтому выбор весовых коэффициентов тоже является
своеобразной задачей и от удачного выбора во многом
зависит время решения задачи.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

134.

134
Теория штрафных функций достаточно хорошо разработана и
основана на идее изменения целевой функции таким
образом, чтобы последовательность точек, получаемых в
результате применения какого-либо метода безусловной
оптимизации, одновременно сходилась и к выполнению всех
ограничений и к минимальному значению целевой функции.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

135.

Пример 3
135
Найти минимум функции
f ( x1 , x2 , x3 ) 1000 x 2 x x x1 x2
2
1
2
2
2
3
При ограничениях:
x x x 25 0
2
1
2
2
2
3
8 x1 14 x2 7 x3 56 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

136.

136
В пакете MatLab для определения минимума с начальными
приближениями: x0 = [3.5, 0.2, 3.5] используется функция
fmincon, которая записывается
[ xopt , Rmin ] fmincon(' f ( x) ' , x0 , [], [], [], [], [], [], ' GL' )
m-файл функции ограничений MatLab имеет вид
function( g1, g 2) GL( x)
g 21 x12 x22 x32 25
g 22 8 x1 14 x2 7 x3 56
g1 [];
g 2 [ g 21, g 22]
end
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а

137.

137
Результат
xopt
0
1.6379
4.7241
Rmin 972.3171
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L3а