Принцип неопределённости Гейзенберга 1927

1.

Гейзенберг, Вернер Карл
(1901-1976)

2.

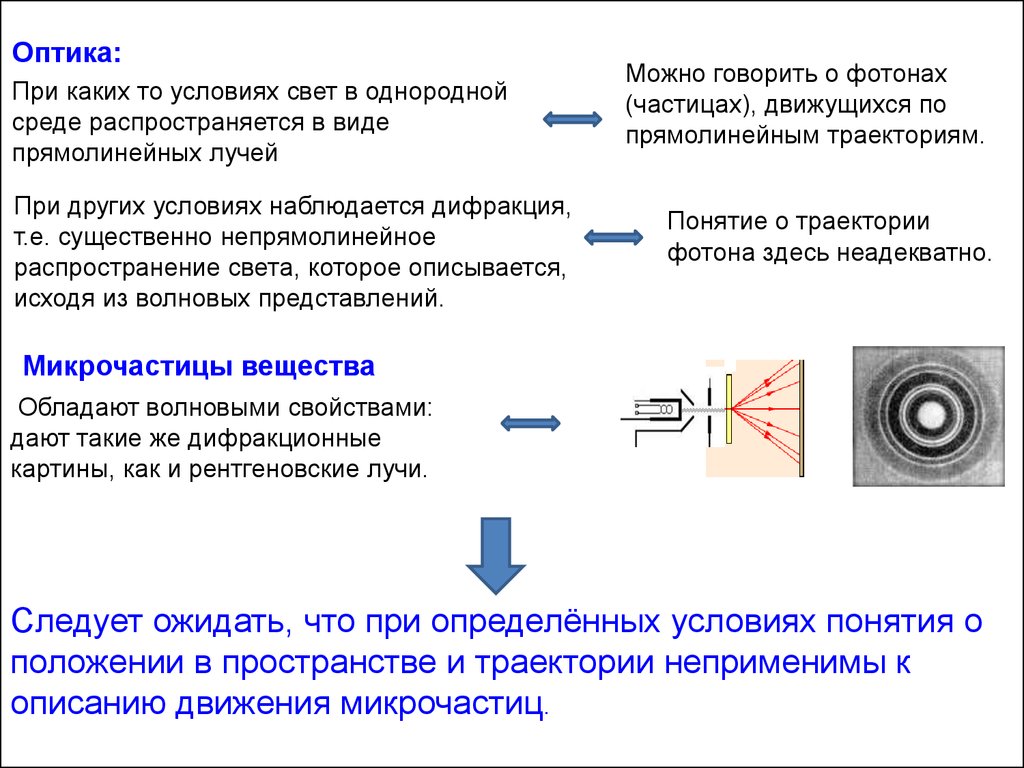
Оптика:
При каких то условиях свет в однородной
среде распространяется в виде
прямолинейных лучей
При других условиях наблюдается дифракция,
т.е. существенно непрямолинейное
распространение света, которое описывается,
исходя из волновых представлений.
Можно говорить о фотонах
(частицах), движущихся по
прямолинейным траекториям.
Понятие о траектории
фотона здесь неадекватно.
Микрочастицы вещества
Обладают волновыми свойствами:
дают такие же дифракционные
картины, как и рентгеновские лучи.
Следует ожидать, что при определённых условиях понятия о
положении в пространстве и траектории неприменимы к
описанию движения микрочастиц.

3.

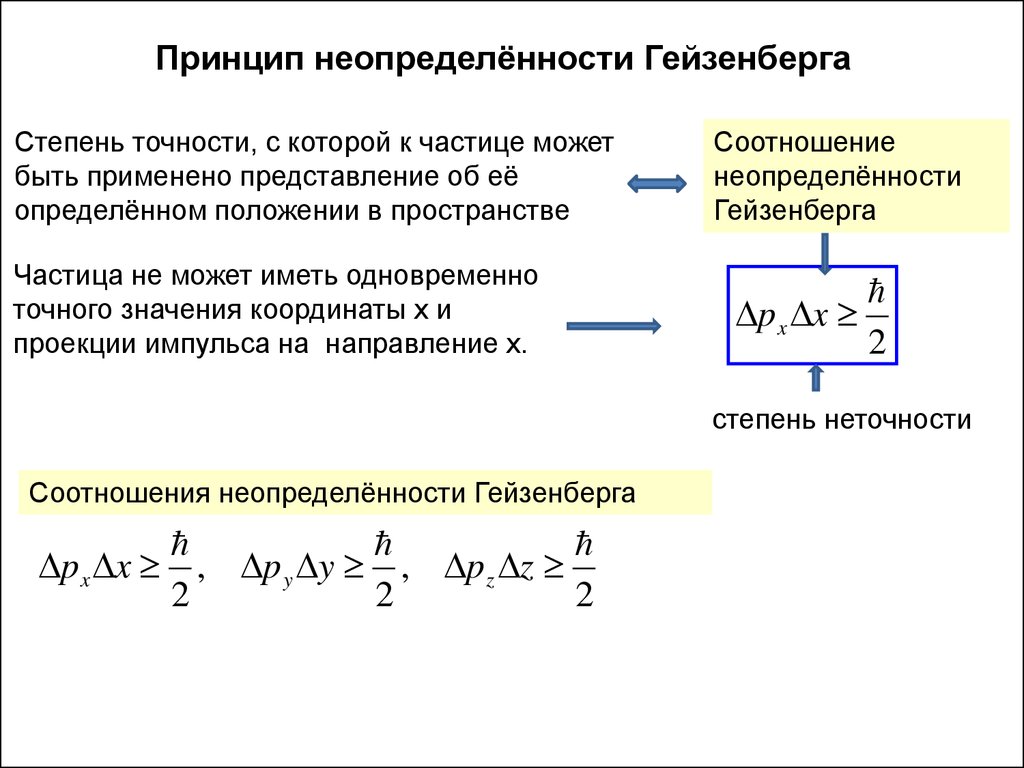
Принцип неопределённости Гейзенберга
Степень точности, с которой к частице может
быть применено представление об её
определённом положении в пространстве
Частица не может иметь одновременно
точного значения координаты x и
проекции импульса на направление x.
Соотношение
неопределённости
Гейзенберга
p x x
2
степень неточности
Соотношения неопределённости Гейзенберга
p x x , p y y , p z z
2
2
2

4.

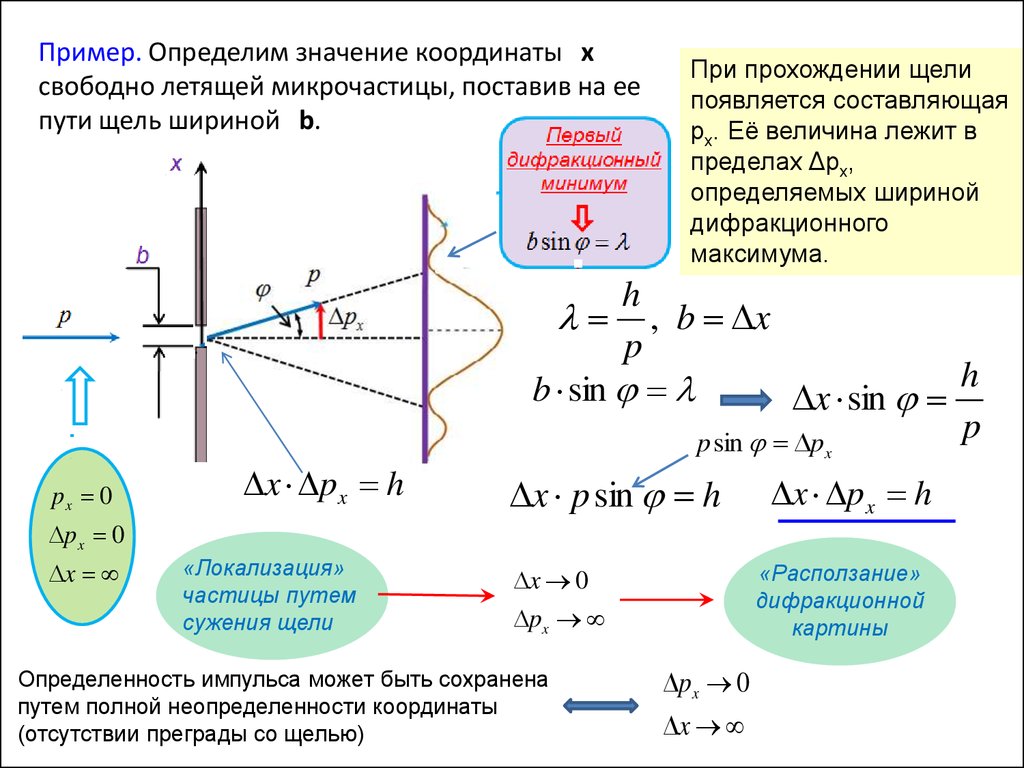
Пример. Определим значение координаты x
cвободно летящей микрочастицы, поставив на ее
пути щель шириной b.
При прохождении щели
появляется составляющая
px. Её величина лежит в
пределах Δpx,
определяемых шириной
дифракционного
максимума.
h
, b x
p
h
b sin
x sin
p
p sin p
px 0
x px h
x
x p sin h
p x 0
x
«Локализация»
частицы путем
сужения щели
«Расползание»
дифракционной
картины
x 0
px
Определенность импульса может быть сохранена
путем полной неопределенности координаты
(отсутствии преграды со щелью)
x px h
px 0
x

5.

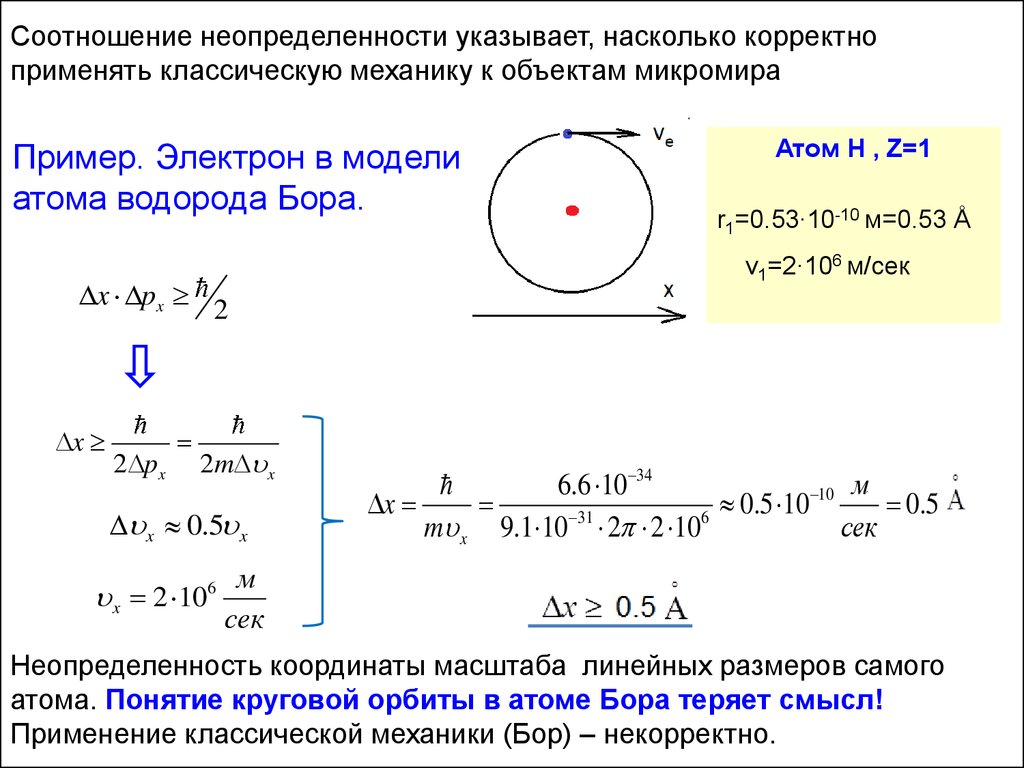
Соотношение неопределенности указывает, насколько корректно
применять классическую механику к объектам микромира
Пример. Электрон в модели
атома водорода Бора.
x px
x
2 px
Атом Н , Z=1
r1=0.53∙10-10 м=0.53 Å
v1=2∙106 м/сек
2
2m x
x 0.5 x
x 2 106
6.6 10 34
10 м
x
0.5 10
0.5
31
6
m x 9.1 10 2 2 10
сек
м
сек
Неопределенность координаты масштаба линейных размеров самого
атома. Понятие круговой орбиты в атоме Бора теряет смысл!
Применение классической механики (Бор) – некорректно.

6.

Пример. Движение электрона в электронно-лучевой трубке
Пятно, которое даёт электронный луч на экране, должно восприниматься глазом.
Соответственно, его радиус не должен быть меньше быть ≈0.1 мм.
Пусть этот размер пятна полностью определяется неопределённостью импульса.
x
p
px
r 0,1мм 10 4 м
L=0,1 м
U=10 кВ
x
x
2 px
L
L
2 pr 2r 2meU
Увеличенное изображение
«пятна» от луча на экране
электронно-лучевой трубки
6,6 10 34 0,1
2 2 3,14 10 4 2 9,1 10 311,6 10 19104
~ 10 9 м
x 10 9 м r 10 4 м
Волновые свойства электронов можно не учитывать. Понятие
траектории – корректно для движения электрона в электроннолучевой трубке. Движение электрона можно рассчитывать по
законам классической механики несмотря на то, что это
микрочастица! Электронная оптика и т.п.

7.

Пример. Пылинка
Линейный размер:
r ≈10-4 см = 1мкм
Будем определять координату пылинки x с точностью
∆x<<r и ∆x<<λ (длины волны
видимого света, ≈5∙10-5 см)
.
Очень высокая точность!
Какова неопределённость определения скорости?
x px
2
6,6 10 34
11 м
x
0,5
10
с
2m x 2 3,14 2 10 15 10 8
Пылинка – большая; у нее большая масса; она объект макромира и к
ней применимы законы классической физики !!

8.

ВОЛНОВАЯ ФУНКЦИЯ
Микрочастицы обладают волновыми свойствами. А именно, их
положение в пространстве задаётся определённым
вероятностным законом и этот вероятностный закон таков, что
при усреднении (по времени или по большому числу частиц)
реализуется волновая картина.
Необходимо создать математический формализм, описывающий наблюдаемые в
микромире явления и правильно предсказывающий поведение микрочастиц.
Описание поведения (состояния)
Такой формализм был создан
микрочастиц с помощью волновой
функции Ψ.
Вводится комплексная волновая функция Ψ, квадрат модуля которой даёт
вероятность обнаружения частицы в пределах объёма dV
Вероятность обнаружения
частицы в объёме dV
Нобелевская
премия за
истолкование
статистического
смысла Ψ
dW dV dV
Плотность вероятности
обнаружения частицы в данной
точке пространства.
2
dW
2
w
dV
*
Макс Борн
(1882-1970)
Для волновой функции Ψ должно быть найдено такое уравнение, чтобы найденная
из него Ψ описывала поведение микрочастиц с учётом их волновых свойств.

9.

U i
2m
t
2
Эрвин Шредингер
(1887-1961)

10.

Уравнение Шредингера
Потенциальная
энергия
2 2 2
( 2 2 2 ) U i
2m x
y
z
t
2
2 2 2
2 2 2
2
x
y
z
2
2m
U i
t
Дифференциальное ур-ие 2-го
порядка в частных производных –
основное ур-ие нерелятивисткой
квантовой механики.
Не выводится – физический закон
Оператор Лапласа
Стационарное уравнение Шредингера.
Если силовое поле, в котором движется частица, стационарно, т.е. не зависит
от времени (U не зависит от t), то уравнение Шредингера имеет вид
Полная энергия
системы
2
2m
( x, y, z ) ( E U ) ( x, y, z ) 0
Стационарное уравнение
Шредингера.
Не зависит от времени

11.

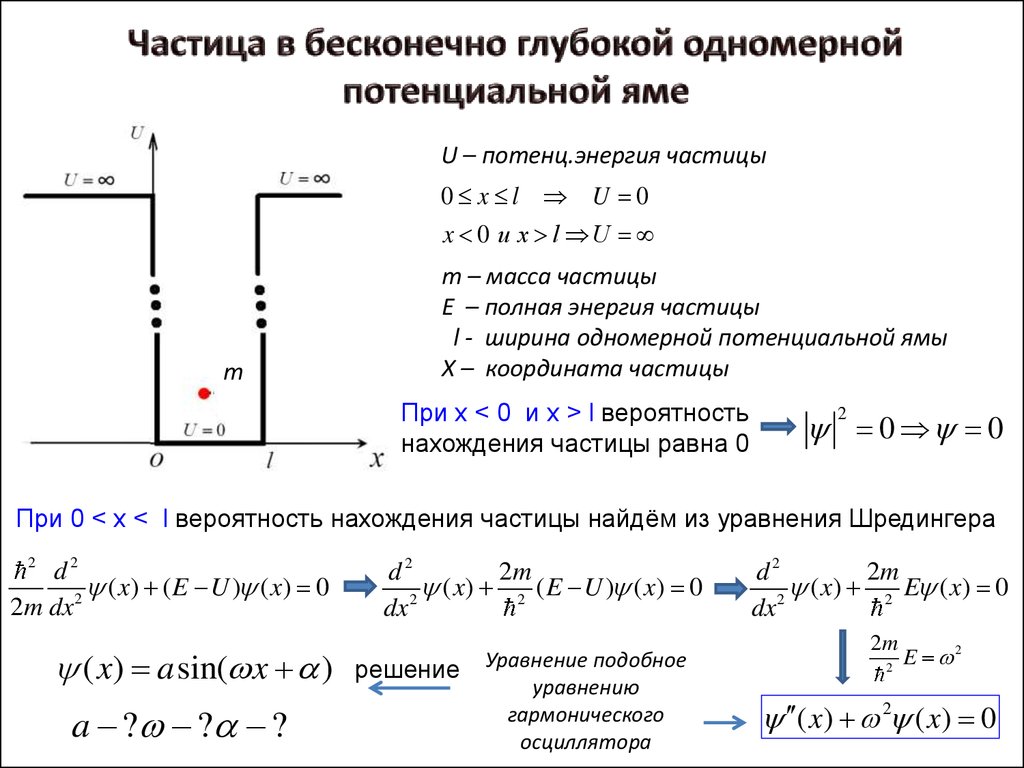
U – потенц.энергия частицы
0 x l U 0
x 0 и x l U
m
m – масса частицы
E – полная энергия частицы
l - ширина одномерной потенциальной ямы
X – координата частицы
При х < 0 и x > l вероятность
нахождения частицы равна 0
0 0
2
При 0 < х < l вероятность нахождения частицы найдём из уравнения Шредингера
2
d2
( x) ( E U ) ( x) 0
2
2m dx
( x) a sin( x )
a ? ? ?
d2
2m
(
x
)
( E U ) ( x) 0
2
2
dx
решение
Уравнение подобное
уравнению
гармонического
осциллятора
d2
2m
(
x
)
E ( x) 0
2
2
dx
2m
2
E 2
( x) 2 ( x) 0

12.

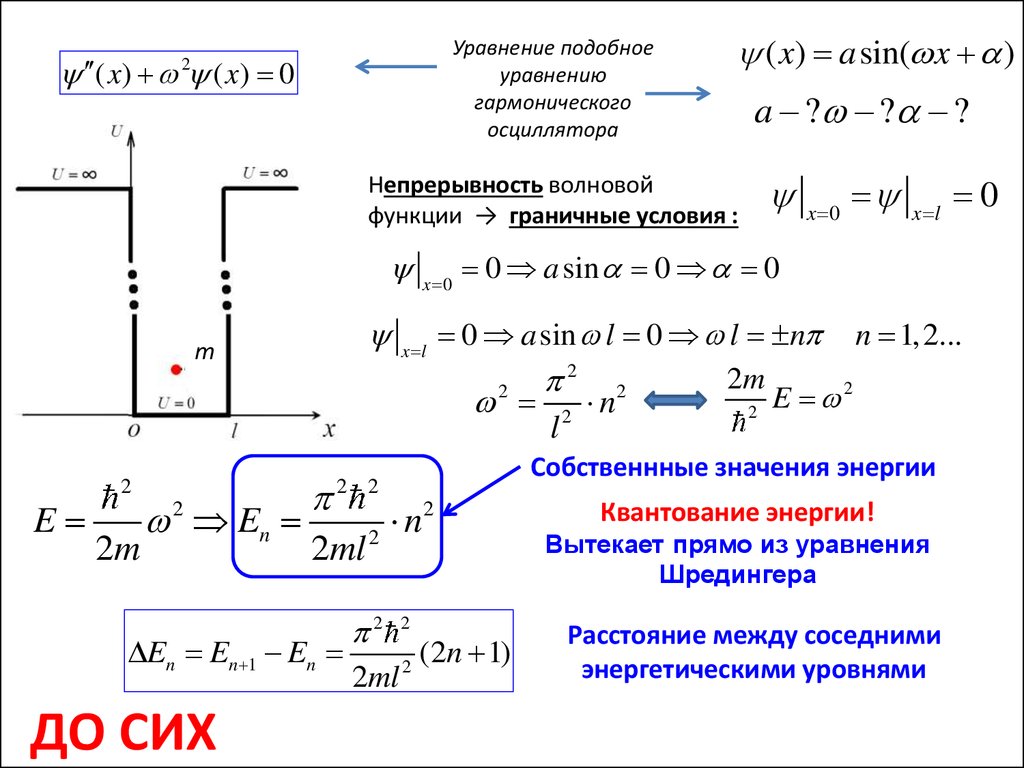
Уравнение подобное
уравнению
гармонического
осциллятора
( x) ( x) 0
2
( x) a sin( x )
Непрерывность волновой
функции → граничные условия :
m
E
2
En
2
2m
x l
2ml
2ml
x 0
x l
Собственнные значения энергии
2
0
0 a sin l 0 l n n 1, 2...
2m
2 2
2
2
E
2 n
2
l
2
n
2
2
0 a sin 0 0
2 2
En En 1 En
ДО СИХ
x 0
a ? ? ?
(2n 1)
2
Квантование энергии!
Вытекает прямо из уравнения
Шредингера
Расстояние между соседними
энергетическими уровнями

13.

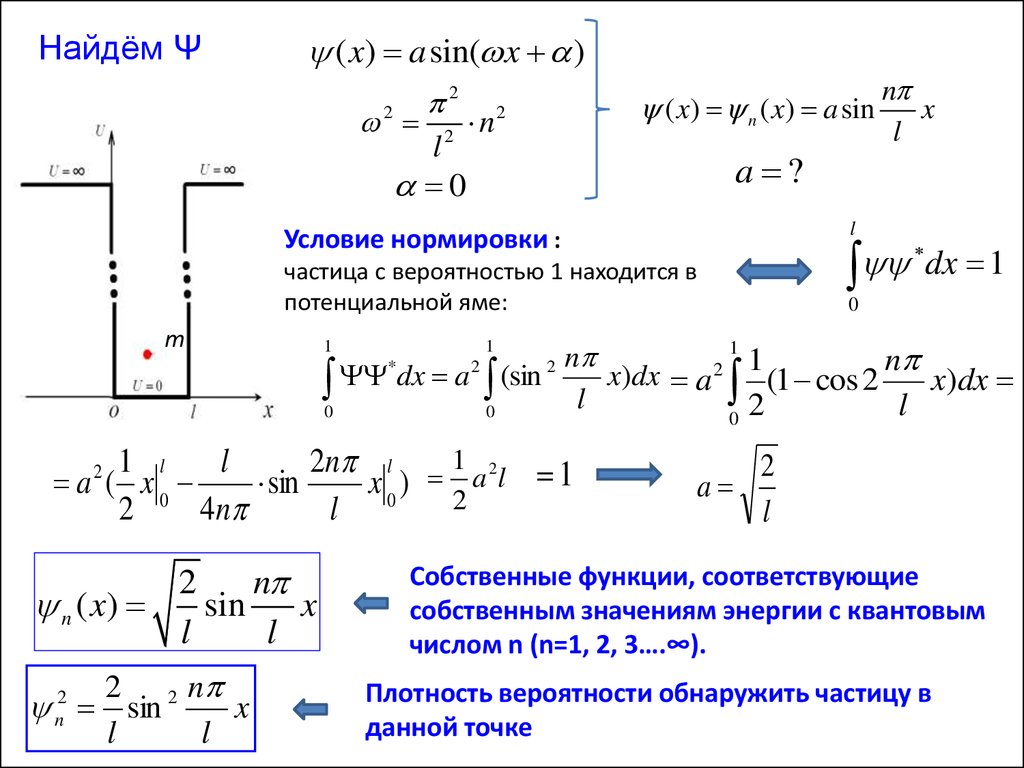
Найдём Ψ
( x) a sin( x )
2
2
2
l
0
n
( x) n ( x) a sin
2
a ?
l
Условие нормировки :
dx 1
частица с вероятностью 1 находится в
потенциальной яме:
m
n
x
l
0
1
n
n
2 1
dx
a
(sin
x
)
dx
a
(
1
cos
2
x)dx
0
0
l
2
l
1
1
*
2
2
0
1 l
l
2n l 1 a 2l 1
a ( x0
sin
x 0) 2
2
4n
l
2
2
n
n ( x)
sin
x
l
l
2 2 n
sin
x
l
l
2
n
2
a
l
Собственные функции, соответствующие
собственным значениям энергии с квантовым
числом n (n=1, 2, 3….∞).
Плотность вероятности обнаружить частицу в
данной точке

14.

Плотность вероятности обнаружить частицу в
данном месте
Квантование энергии
En
2 2
2ml
2
n
2
n ( x)
2
n
sin
x
l
l
2
En
o
E4
2 2 n
sin
x
l
l
2
n
n 4
o
n 3
o
n 1
n 2
o
o
o
E3
E2
E1
l
0
En
2
2ml
2
(2n 1)
2
m ...
l ...
x
0
Классическая
физика
l
x

15.

Найдём масштаб квантования энергии.
Пример 1: электрон, m≈10-30 кг, размер ямы l=10 см (свободный электрон
в металле)
2 2
2
2
68
6
.
6
10
37
18
n
En
(
2
n
1
)
n
10
n
Дж
10
n эВ
2
2
2
30
2
ml
2ml
4 10 10
2
2
Спектр энергии – практически непрерывный
классическая физика
Пример 2: электрон, размер ямы l ≈ 10-8 см
Размеры области
порядка размера атома
2 6.62 10 68
19
n
10
n Дж 1n эВ(!!)
En
n
2
30
20
2
4 10 10
ml
2 2
Энергия квантована!

16.

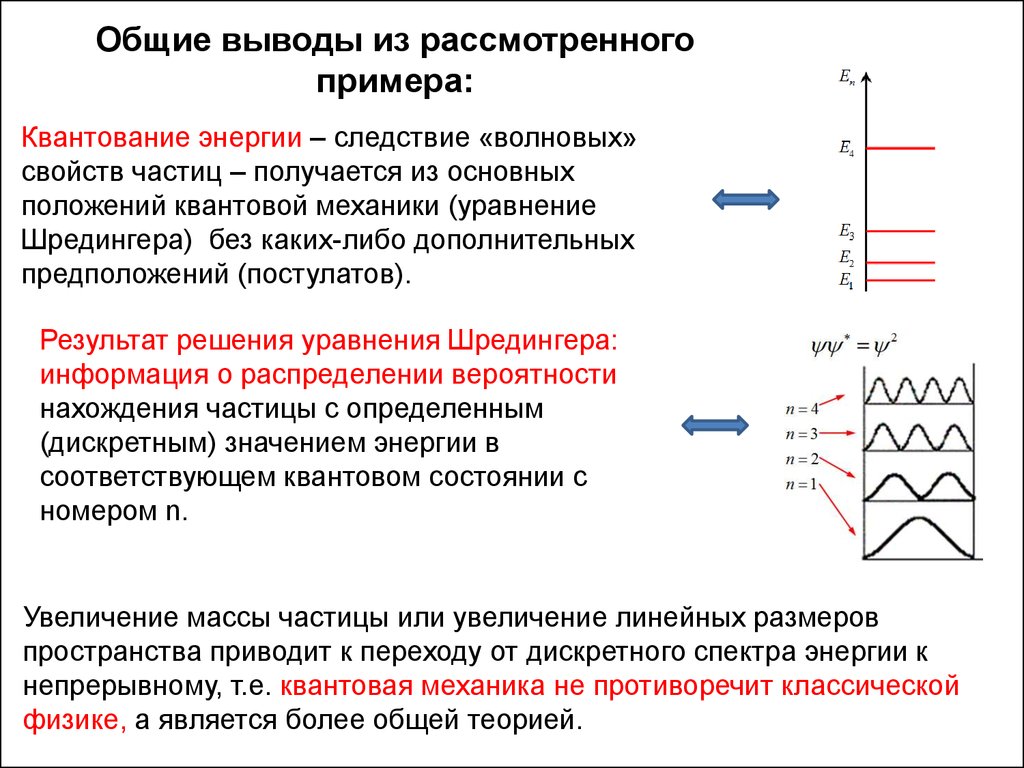
Общие выводы из рассмотренного
примера:
Квантование энергии – следствие «волновых»
свойств частиц – получается из основных
положений квантовой механики (уравнение
Шредингера) без каких-либо дополнительных
предположений (постулатов).
Результат решения уравнения Шредингера:
информация о распределении вероятности
нахождения частицы с определенным
(дискретным) значением энергии в
соответствующем квантовом состоянии с
номером n.
Увеличение массы частицы или увеличение линейных размеров
пространства приводит к переходу от дискретного спектра энергии к
непрерывному, т.е. квантовая механика не противоречит классической
физике, а является более общей теорией.

17.

18.

Решение уравнения Шредингера для электрона в
центрально-симметричном поле ядра
Система: ядро с зарядом +Ze и один электрон
Полная энергия
системы
2
2m
Потенциальная
энергия системы
( x, y, z ) ( E U ) ( x, y, z ) 0
Ze2
U
4 0 r
Ур-е Шредингера
Можно показать: уравнение Шредингера имеет
однозначные, конечные и непрерывные решения
при любых положительных значениях полной
энергии: Е>0 (свободный электрон) ;
при дискретных отрицательных значениях
полной энергии: E<0 (связанный электрон).
Результат решения:
собственные
значения энергии
me Z 2e 4 1
En 2 2 2
8h 0 n
n = 1,2,3,…
Совпадает с Еn, полученной Бором (!!). Но здесь получается из ур-я Шредингера без каких
либо дополнительных предположений (типа постулатов Бора).

19.

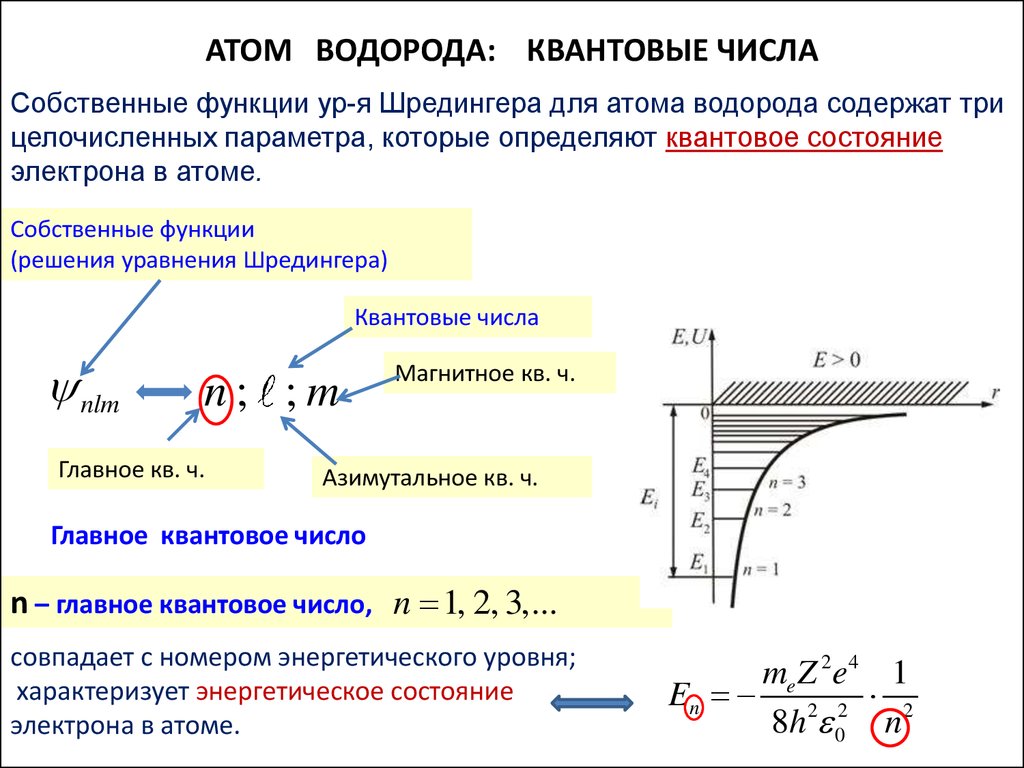
АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА
Собственные функции ур-я Шредингера для атома водорода содержат три
целочисленных параметра, которые определяют квантовое состояние
электрона в атоме.
Собственные функции
(решения уравнения Шредингера)
Квантовые числа
nlm
n; ;m
Главное кв. ч.
Магнитное кв. ч.
Азимутальное кв. ч.
Главное квантовое число
n – главное квантовое число, n 1, 2, 3,...
совпадает с номером энергетического уровня;
характеризует энергетическое состояние
электрона в атоме.
me Z 2e 4 1
En 2 2 2
8h 0 n

20.

АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА
nlm
n; ;m
Азимутальное квантовое число
– азимутальное квантовое число
0,1, 2, ....n 1
определяет величину (модуль) момента импульса электрона в атоме:
L
Величина момента импульса квантована
( 1)
n 1 l 0, L 0
(!)
В отличие от модели Бора (!!)
l 0, L 0
n 2
l 0, L 0
l 1, L 2
n 3 l 1, L 2
l 2, L 6
n 4. .............

21.

АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА
nlm
n; ;m
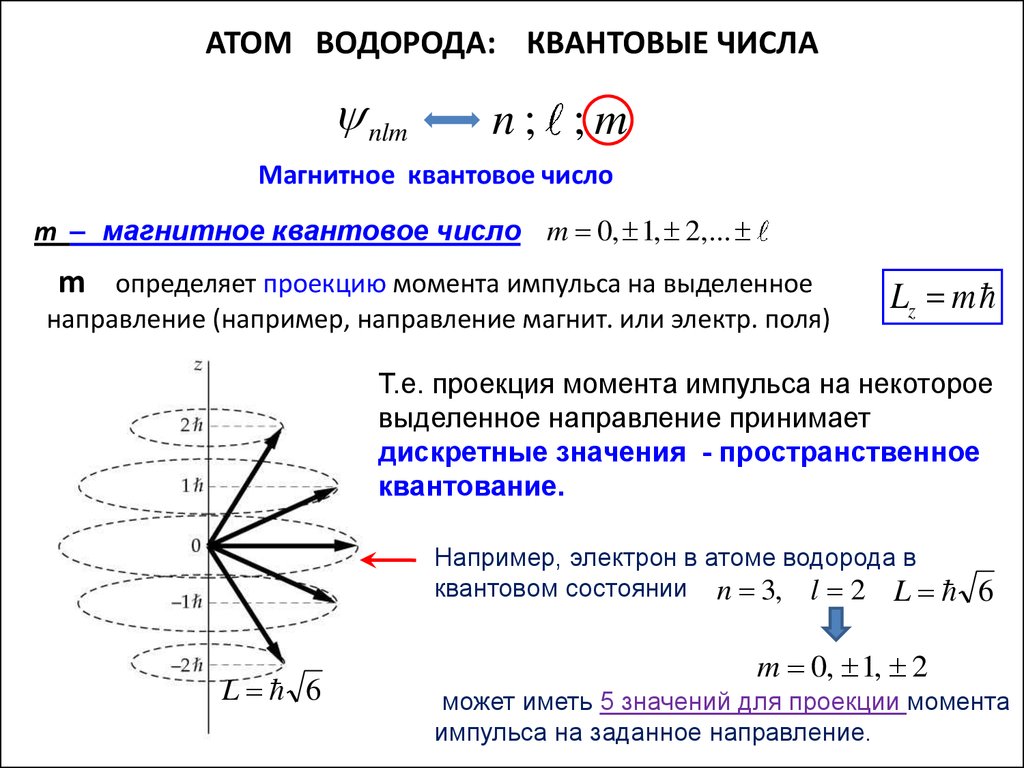
Магнитное квантовое число
m – магнитное квантовое число m 0, 1, 2,...
m определяет проекцию момента импульса на выделенное
направление (например, направление магнит. или электр. поля)
Lz m
Т.е. проекция момента импульса на некоторое
выделенное направление принимает
дискретные значения - пространственное
квантование.
Например, электрон в атоме водорода в
квантовом состоянии n 3, l 2 L
L 6
6
m 0, 1, 2
может иметь 5 значений для проекции момента
импульса на заданное направление.

22.

АТОМ ВОДОРОДА: ВЫРОЖДЕННЫЕ СОСТОЯНИЯ
nlm
n – главное квантовое число,
n; ;m
n 1, 2, 3,...
– азимутальное квантовое число
m – магнитное квантовое число
me Z 2e 4 1
En 2 2 2
8h 0 n
0,1, 2, ....n 1
m 0, 1, 2,...
Энергия зависит только от n
Одному энергетическому состоянию может соответствовать несколько
квантовых состояний электрона – вырожденные состояния.
Число вырожденных состояний – кратность вырождения .
1 2(n 1) 1
(2 1)
n n2
2
0
n 1
n
2

23.

АТОМ ВОДОРОДА:
РАЗЛИЧНЫЕ КВАНТОВЫЕ СОСТОЯНИЯ, ОРБИТАЛИ
En
1
nlm
n
m
1s
0 1 2 3...
s p d
2s
4
2p
3s
3p
9
3d
f ...

24.

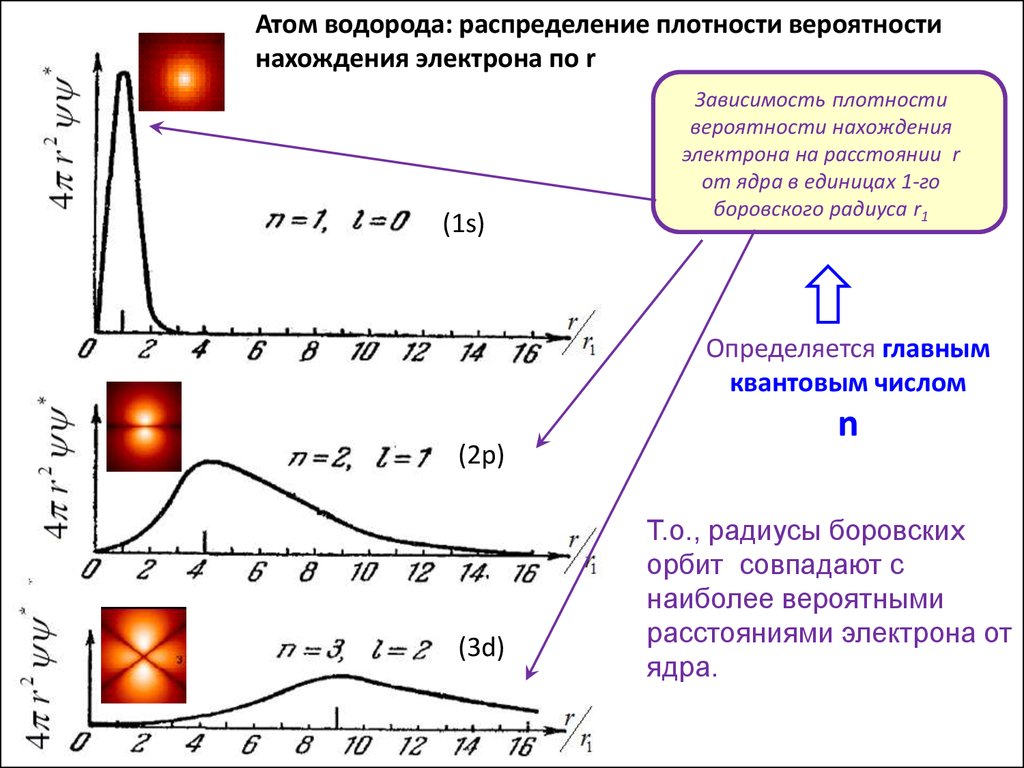
Атом водорода: распределение плотности вероятности
нахождения электрона по r
(1s)
Зависимость плотности
вероятности нахождения
электрона на расстоянии r
от ядра в единицах 1-го
боровского радиуса r1
Определяется главным
квантовым числом
(2p)
(3d)
n
Т.о., радиусы боровских
орбит совпадают с
наиболее вероятными
расстояниями электрона от
ядра.